Estimating Quadratic Cost Curve Coefficients of Thermal Power Plant Without Using Fuel Input Data

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 12 | Dec 2022 www.irjet.net p-ISSN: 2395-0072

Estimating Quadratic Cost Curve Coefficients of Thermal Power Plant Without Using Fuel Input Data

1,2Department of Electrical and Electronics Engineering, Modibbo Adama University, Yola Nigeria ***

Abstract - Solvingeconomicdispatchproblemsonapower system inevitably require the fuel cost curve coefficients. Therefore, accurateandfrequentupdatingofthesecoefficients is very important to improve the accuracy of economic dispatch solutions. At times the data needed to compute the cost curve coefficients may not be available. This paper presents an approach to estimate the quadratic cost coefficientsofathermalpowerplantwhenthe fuel inputdata iscompletelynotavailable.Theaverageheatrateatminimum operating capacity of the power plant is computed using the average heat rate at maximum capacity available on U. S. Energy Information Administration website and the type of turbine used. Intermediary heat rate values are computed usingfinitedifferencemethod. Thefuelinputcorrespondingto each heat rate and corresponding power output level is computed to generate the required fuel input versus power output data set. The cost curve coefficients are determined using least square estimation method. The proposal is demonstrated on some Nigeria thermal power plants. The coefficients obtained are compared with values available in recent literature. Coefficients obtained using this proposed method differ from the coefficients in recent literature by maximum of error of 27% over those in literature.

Key Words: Cost curve coefficients, Economic Load Dispatch,LeastSquareEstimation,Finitedifferencemethod, ThermalPowerPlant,Steamturbinevalvepointeffect

1.INTRODUCTION

The input-output curve which is a plot of fuel input in Britishthermalunitperhourversusnetrealpoweroutputis averyimportantcharacteristicsofathermalpowerplantin economic operation perspective. There are other characteristic curves that indicate the economic performanceofthethermalplantthatcanbederivedfrom theinput-outputcurve.Theyincludefuel-costcurvewhichis theinput-outputcurvescaledbytheunitcostoffuel,heatrate curve (ratio of the input fuel to the corresponding output power plotted against power output) and the incrementalcostcurvewhichplotstheincrementalcostasa functionofpoweroutput.Theincrementalfuelcostcanbe obtainedbydifferentiatingthecostcurvewithrespecttothe poweroutput[1].

Thebestpolynomialoffittothefuelcostcurveisthefuel costfunctionandthecoefficientsofthepolynomialarethe

fuel cost coefficients. The fuel cost coefficients are particularly important because the accuracy of economic dispatchproblemsisassociatedwiththeaccuracyofthefuel costcurvecoefficients.Therefore,determiningorupdating thesecoefficientsisaveryimportantissuetoachieveoverall accuracy of economic dispatch solutions. [2]The general mathematicalmodelofthepolynomialoffittothecostcurve ofapowerplantis;

… (1)

where F(Pg)is the fuel cost function of the plant, Pg is the electrical power output of theplant in MW, aj arethecost coefficientsfortheplant, j istheequationorder(1forlinear, 2forsecond-order,3forcubicandsoon)andristheerror associatedwiththemodelling.Thecoefficient represents thefixedcostswhichismadeupofthecapitalinvestment, interestcharged onthemoney borrowed,taxpaid,labour charge, salary given to staff and any other non-fuel dependentexpenses.Duringthecourseofplantoperation, the re-estimation of cost coefficients is required due to fluctuationsinvariouscosts andageingofthepowerunit. The higher the accuracy of the estimated coefficients, the more accurate the results obtained from the economic dispatchcalculations.Severalclassicalmethodstocalculate theinput-outputcharacteristicshaveappearedinliterature, such as the quadratic least square regression method [3]. The cost curve coefficients estimation has also been formulatedasanoptimizationproblemwheretheestimation error is minimized. Heuristic methods such as particle swarmoptimizationalgorithm[4],geneticalgorithm[3,5], Nelder-MEADLocalSearchalgorithm[6]andCuckooSearch [7] have been employed to minimize the error associated withtheestimatedcoefficients

Themajorrequirementfortheestimationofthecost curvecoefficientsisasetoffuelinput–poweroutputpairs whichareoftenderivedfromtestsontheindividualthermal generator. At times these data set may not be available. ProbablyitisthelackofdatathatmotivatedAndreas[8]to proposeatechniquefortheapproximationoftheheatrate curvewhichcanbeappliedforpowerplantsinwhichdata areavailableonlyatthemaximumandminimumoperating capacitiesofthepowerplant.Thisstillrequireddatapairs, thoughonlytwo. Theworkproposedhereisanattemptto estimatethequadraticcostcurvecoefficientswhenthefuel

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 12 | Dec 2022 www.irjet.net p-ISSN: 2395-0072

inputdataiscompletelyunavailable.Thefuelinputforthe maximumandminimumoperatingcapacitiesarecomputed usingtheknowledgeoftheaverageheatrateatfullcapacity and the type of turbine used. Intermediary values of heat ratearedeterminedusingthemethodoffinitedifference.In thiswaytherequiredinput–outputsetofdataisgenerated. Theleastsquareestimationmethodisthenusedtocompute thecostcurvecoefficients.

2. METHODOLOGY

2.1 Estimation of Fixed Cost

The fixed cost is made up of the capital investment, interest charged on money borrowed, tax paid, labour charge,salarygiventostaffandotherexpensesthatcontinue irrespective of the load on the power plant. To derive the fixedcost,adetailedcostanalysismustbepreparedforthe plant.Theeconomicoperationofanelectricalpowersystem canbeachievedbyminimizingthevariablecostsonlywhile the personnel in charge of the plant operation have little control over the fixed costs. This work therefore does not considertheestimationofthefixedcostssincetheydonot affecteconomicdispatchcalculations.

2.2 Computation of Fuel Cost

Theamountoffuelusedtogenerateelectricitydepends ontheefficiencyorheatrateofthegeneratorandtheheat contentofthefuelbeingused.Generatorheatratevariesby type of generator prime mover, power plant emission controls, and other factors. The heat content of different fuelsalsovaries.

A fundamental formula that can be used to calculate the amount of fuel used to generate a kilo watthour (kWh) of electricityis[9];

AmountoffuelusedperkWh=Heatrate(inBritishThermal Units (Btu)perkWh) dividedbyFuel heatcontent(inBtu perphysicalunit) … (2)

Fornaturalgas,theAverageBtupercubicfootis1000per cubicfootsothattheamountoffuelusedis;

AmountoffuelusedperkWh= cubicfeet … (3)

1cubicfeetofnaturalgas[10]=1000Btu … (4)

Theamountoffuelrequiredisthen,

Amountoffuelused= BtuperkWh … (5)

Ifthepowergenerationlevel(P)isgiveninMW,then;

Amountoffuelused= Btuperhour … (6)

Theaveragetestedheatrates( )intheyear2020forfull loadconditionsfordifferentprimemoversfornaturalgas areasgiveninTable1

Table -1: AverageTestedHeatRates[11]

Primemovertype Averagetestedheatrate

Steamgenerator 10347 Gasturbine 11,098 Internalcombustion 8,899 Combinedcycle 7633

The average tested heat rate is reported at full load conditions (Pmax) sothatthemaximumfuelinput(Fmax)is; Btuperhour … (7)

The heat rate at minimum generation can be approximatedwith, … (8)

Haven obtained the heat rate at maximum and minimum generationcapacities,theone-dimensional finitedifferencemethod[12]isappliedtogettheheatrate values forotherlevelsofgeneration.

Inapplyingthefinitedifferencemethod,theinterval to is divided into N-1equal intervals and the step of approximationh,iscalculatedthus.

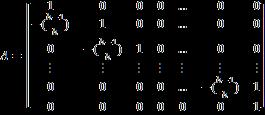
… (9)

Thenusingfinitedifferences,theapproximateintermediary heat ratevaluescanbeobtainedusing[7]; … (10)

Expandingequation(10)andrearranginggives … (11)

Where … (12)

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 12 | Dec 2022 www.irjet.net p-ISSN: 2395-0072

for which the predicted values of the curve minimize the sumofthesquareddeviationsgivenby;

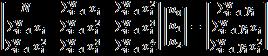
… (17)

… (13)

Thefuelinputforeveryheatratevalueiscomputedas; … (14)

2.3 Treatment of Steam Turbine Plants

Forsteamturbinegenerator,theinput-outputcurve is non-linear and also non convex when it has multiple admissionvalves.[4].Forsuchgenerators,theinput–output characteristics are not always smooth because the steam admission valves are opened in sequence for more steam intake thereby producing ripples in the input–output characteristics. In this situation the fuel input function is modeledbyaddingasinusoidtermasinequation(15)

… (15) Where , arethefuelcostcoefficientsofthe ith unit, and arethefuelcostcoefficientsofthe ith unitvalve-point effects[4,13,14]. Therefore,forsteamturbinegenerators, after getting the fuel input and power output pairs using equations(13)and(14),theresultshavetoberefinedusing equation(15)totakeintoaccountthevalvepointeffect. If theaveragecostrateofnaturalgasis,say,R$permillion British thermal units (mmBtu), then the fuel inputs are convertedtofuelcosts(CF)asinequation(16).

… (16)

Thecoefficientsofquadraticpolynomialofbestfittothefuel costsfunctionaredeterminedusingmethodofleastsquare estimation.

2.4 The Least Square Estimation (LSE)

The least square estimation LSE is a method used to performcurvefittingoninput-outputdata.Thepolynomial offitcanbeanyorderandthemajortaskistodeterminethe coefficients of the polynomial of fit. The quadratic cost curve,forexample,isasecondorderpolynomialsothethree coefficients and needtobedetermined.LSErequires threeor moredata pointsandis based on minimizingthe sumofthesquarederrorsbetweenthedatapointsandthose onthepolynomialoffit.Forthequadraticcurvefitting,itis intended to determine and such that fitsthedata inthesenseofleast square.Theleastsquareestimates and arethose

Findingtheminimizingvalues and inequation(17) istosolvetheequationsresultingfromsetting,

… (18)

Solving equation (18) implies solving equation (19) to determine and [15].

… (19)

TheLSEcanbeimplementedinMATLABenvironmentusing polyfit command.Theusageformofthe polyfit commandis asfollows.

… (20)

wherePisarowvectorofpoweroutputs,Fisarowvector ofactualcostwhilejispowerofpolynomialtobefitforP andF.Thefunctionreturnsxwhichisarowvectoroflength j containing the polynomial coefficients in descending powersofP.

2.5 Case Study

FourNigerianthermalpowerplantsnamelyEgbinST2-5 (Combinecycle),DeltaII-III,AfamIV-VandSapele(steam) powerplantsareusedascasestudy.Theirgenerationlimits are[16],118MW≤PEgbin≤1100MW,10MW≤PDelta≤110MW, 24MW≤PAfam≤543MWand33MW≤PSapele≤223MW.Thecost rateofnaturalgasinMay2019whichis5.65$permillion Britishthermalunit(mmBtu)[18]isused.

3. RESULTS AND DISCUSSION

Nineincrementalstepsaretakentogettenpowerandfuel input sample points. The fuel input in $ per hour at each samplepointforeachofthegaspowerplantsarecalculated using equation (12). For the steam plant equation (12) is usedandrefinedusingequation(15)sothatthevalvepoint effect is taken into consideration. The valve point effect coefficients for Sapele power plant are and [16].Thepoweroutputandthecomputedfuel input at each sample point are given in Table 2. The quadraticcostcurvecoefficientsobtainedusingthemethod ofleastsquareestimationandtheexactvaluesavailablein literature [16] are presented in Table 3. Percentage error betweentheestimatedcoefficients(estimated)andthosein literature(literaturevalue)arecomputedasinequation(21) andarealsopresentedinTable3.

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page210

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

… (21)

Table -2: Computedfuelinputandcorrespondinggenerationlevel

Powerplant Egbin Delta Afam Sapele TurbineType CombineCycle SimpleCycle SimpleCycle Steam Generation level andfuelinput Generation Level(MW) Fuel cost ( /h) Generation Level(MW) Fuel cost ( /h) Generation Level(MW) Fuel cost ( /h) Generation Level(MW) Fuel cost ( /h) 118.00 528 10.00 551 24.00 77 33.00 276 227.10 2198 21.11 2791 71.67 807 54.11 817 336.20 5010 32.22 6753 119.33 2306 75.22 1643 445.30 8965 43.33 12438 167.00 4575 96.33 2755 554.40 14063 54.44 19846 214.67 7615 117.44 4154 663.60 20303 65.56 28977 262.33 11424 138.56 5838 772.70 27686 76.67 39831 310.00 16003 159.67 7809 881.80 36211 87.78 52407 357.67 21352 180.78 10065 990.90 45879 98.89 66706 405.33 27471 201.89 12608 1100.00 56690 110.00 82728 453.00 34360 223.00 15437

Table -3: Thermalplants’quadraticcostcoefficients

Power Plant CostCoefficients[Proposedmethod] CostCoefficientsinliterature[16] Generationlimits[17] Linear Coefficients ( ) Quadratic Coefficients( ) Linear Coefficients ( )

( ) Error(%) ( ) Error(%)

Quadratic Coefficients( )

Egbin 0.0234 17.61 2.93 25.26 0.0284 3.92 118 1100 Afam 0.0264 8.65 1.48 27.09 0.0289 2.03 24 453

Delta 0.0291 10.74 7.17 10.82 0.0326 6.47 10 110 Sapele 0.0177 21.68 6.82 15.80 0.0226 8.10 33 223

Cost of generating electricity is not the same for all generatingplants.Itdependsuponthefuelconsumptionrate oroperating efficiency, age oftheplant and fuel cost rate. Cost curve coefficients are also affected by these factors, therefore methods of cost curve estimation should not be evaluated by comparing its results with results of similar workinliteratureexceptiftheplantsfuelconsumptionrate, operatingefficiencyandageareequalwhichhardlyhappens. This is why, for example, the cost coefficients in [16] are quitedifferentfromthosein[19]eventhoughtheyarefor the same power plants. Evaluation of this work should thereforebebasedontheobjectivityoftheprocedure.

Nevertheless, comparison have been done here and the resultsinthisworkdifferfromresultsavailableinliterature byamaximumof27%.Theseresultsarethereforeaccurate enoughtobeusedinsolvingeconomicdispatchproblems.

5. CONCLUSION

Asimpletoapplymethodofestimatingquadraticcostcurve coefficientsofthermalpowerplantswhenfuelinputdatais completelynotavailablehasbeendevelopedandpresented in this work. The fuel input corresponding to a particular levelofpoweroutputiscomputedusingtheheatcontentof

Volume: 09 Issue: 12 | Dec 2022 www.irjet.net p-ISSN: 2395-0072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page211

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 09 Issue: 12 | Dec 2022 www.irjet.net p-ISSN: 2395-0072

fuelandthetypeofpowerplantinuse.Inthisway,fuelinput versus power output set of data are generated. Method of least square estimation is used to compute the fuel cost coefficientsTheproposalisdemonstratedonsomeNigerian thermal power plants. The coefficients obtained are comparedwithvaluesavailableinrecentliteratureforthe samepowerplants.Resultsobtainedshowthatcoefficients obtained by this proposed method differ from those availableinrecentliteraturebymaximumof27%overthose inliterature.

REFERENCES

[1] Arunesh Dutt and Ashish Dhamanda (2013) Classical ApproachtoSolveEconomicLoadDispatchProblemof Thermal Generating Unit in MATLAB Programming. International Journal of Engineering Research & Technology2(10)pp1384-1389

[2] Yusuf SÖNMEZ (2013) Estimation of Fuel Cost Curve Parameters for Thermal Power Plants Using the ABC Algorithm Turkish Journal of Electrical Engineering &ComputerSciences21:1827–1841Doi:10.3906/Elk1203-10

[3] DedyK.Setiawan,andRinaAnggraeni,(2017)Analysis of Input-Output Characteristic and Generation Cost OptimizationUsingQuadraticLeastSquareRegression and Dynamic Genetic Algorithm Method: Case StudyPT.PLN PJB UP Gresik, American Institute of Physics Conference Proceedings1818, 020075; Doi: 10.1063/1.4979942

[4] K EL-Naggar, K.M., AlRashidi, M.R., & Al-Othman, A.K. (2009). Estimating the input-output parameters of thermalpowerplantsusingPSO.EnergyConversionand Management, 50(7), 1767-1772. Doi:101016/jenconman200903019

[5] A.M.AL-Khandhar,EL-Naggar,Ageneticbasedalgorithm foroptimalestimationofInput-outputcurveparameters ofthermalpowerplants,electricalengineering,vol89, pp-585-590,2006.

[6] C.V.GopalaKrishnaRao,G.Yesuratnam,G.Ravindranath, G.Sirisha(2018)EstimationofFuelCostParametersfor Thermal Power Plants Using LSE-Nelder-MEAD Local Search (Lse-Nm) Optimization. National Conference Proceeding;NationalConferenceOnTrendsinScience, Engineering & Technology By Matrusri Engineering College &International Journal of Creative Research Thoughts(IJCRT);IJCRTNTSETFeb2018|ISSN:23202882

[7] V.K.Abanihi and K.O. Ovabor(2019)EconomicLoad DispatchofNigeriaIntegratedHigh

[8] Voltage Generation and Transmission Grid Using Bat Algorithm.NigerianJournalofTechnology(NIJOTECH) Vol. 38, No. 3, pp. 680 – 687 www.nijotech.com http://dx.doi.org/10.4314/njt.v38i3.20

[9] U.S. Department of Energy, Energy Information Administration website: https://www.eia.gov/tools/faqs/faq.php?id=667&t=3ac cessed10November2019

[10] Cubic Feet of Natural Gas to British Thermal UnitsKyle's Converter http://www.kylesconverter.com/energy,-work,-andheat/cubic-feet-of-natural-gas-to-british-thermal-units

[11] U.S. Department of Energy, Energy Information Administrationwebsite:AverageTestedHeatRatesby Prime Mover and Energy Source, 2007 – 2017 https://www.eia.gov/electricity/annual/html/epa_08_0 2.htmlaccessed10November2019R.Nicole,

[12] R.Lakshmi,M.Muthuselvi(2013),NumericalSolution for Boundary Value Problem Using Finite Difference Method,InternationalJournalofInnovativeResearchin Science, Engineering and Technology Vol. 2, Issue 10, October2013p5305-5313

[13] RameshKY&MadhavSK2018.Solvingeconomicload dispatchproblemwithvalvepointeffect.International ResearchJournalofEngineeringandTechnology,5(11): 1481–1485.

[14] AwodijiOO&KomlaAF2015.Economicloaddispatchof powersystemusinggeneticalgorithmwithvalvepoint effect. Springer International Publishing Switzerland, 1(1):276–284.

[15] Temitope Adefarati, Ayodele Sunday Oluwole and Mufutau Adewolu (2013) Computational Solution to Economic Operation of Power Plants. Electrical and Electronic Engineering, 3(6): 139-148 DOI: 10.5923/j.eee.20130306.01K.Elissa, N. Ndunagu, V. K. Abanihi and S. Ikheloa (2019) Economic Load Dispatch of Nigerian Power Network Using a Hybrid of Evolutionary Programming and EfficientParticleSwarmOptimization,FUWTrendsin Science&TechnologyJournal,Vol.4No.3pp.697–702

[16] J. N. Ndunagu, V. K. Abanihi and S. Ikheloa (2019) Economic Load Dispatch of Nigerian Power NetworkUsingaHybridofEvolutionaryProgramming andEfficientParticleSwarmOptimization,FUWTrends inScience&TechnologyJournal,Vol.4No.3pp.697–702

[17] [9] U.S. Department of Energy, Energy Information Administration website:

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

https://www.eia.gov/tools/faqs/faq.php?id=667&t=3ac cessed10November2019

[18] U.S. Department of Energy, Energy Information Administration website: henry hub natural gas spot price (dollars per million Btu). www.eia.gov/dnav/ng/hist/rngwhhdm.htm. Accessed 26May2019

[19] Y.S.Haruna,Y.A.Yisah,G.A.Bakare,M.S.HarunaandS. O.Oodo(2017),OptimalEconomicLoadDispatchofthe NigerianThermalPowerStationsUsingParticleSwarm Optimization (PSO), The International Journal of EngineeringandScience(IJES),Volume6Issue1PP1723DOI:10.9790/1813-0601021723

Volume: 09 Issue: 12 | Dec 2022 www.irjet.net p-ISSN: 2395-0072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page