Inelastic seismic response of diagrid structure under critical seismic zone due to bi-directional gr

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

Inelastic seismic response of diagrid structure under critical seismic zone due to bi-directional ground motion

Utsha Chowdhury1, Krishnendu Chowdhury2

1,2Assistant Professor, Department of Civil Engineering, K K College of Engineering & Management, Jharkhand, India ***

Abstract – The innovative diagrid structural system has emerged with an aesthetic architectural view in the design of tall building structures. Nonlinear dynamic analysis is investigating the response of diagrid structural system under critical seismic zone owing to bi-directional excitation has been reported. Furthermore, in this study, the seismic performance of square and circular diagrid structures with different brace angles are compared to sustain the stability in critical seismic zone in India. Seismically operated asymmetric structures are more vulnerable than symmetric structures because of the coupling of lateral and torsional vibration. For this purpose, asymmetric system makes a challenging issue to determine the critical response of load resisting elements for serviceability. Structures are generally experienced on degradation matter of stiffness and strength in the event of strong seismic excitation. In that case, the structural deterioration occurs due to the external loads, clearly demonstrates that the elements have large amount of losses and fragility finitely A broad conclusion presents in this study that to help the fine tune of the seismic code provisions

Key Words: Inelastic response, Seismic response, Bi-directional, Angle of brace, Near-fault, Critical zone.

1. INTRODUCTION

SeismicanalysisofR/Cstructureisnecessaryaspectintherecentpast.Generally,diagridstructureislightweightstructure compellingagainstgravityandalsoresistingtheexcessseismicloading,controlledasmuchaspossiblecomparedtoother complexstructuresreasonably.TheDiagridstructuresarecomposedoftriangulatedsectionswhichcombattheseismicforces byaxialactionofdiagonalsprovidedonperiphery. Structuraldesignfordiagridsystemisgovernedbyhorizontalforcedueto lateralloadslikeearthquake,windloadetc.whichresistiblebytheexteriorandinteriorstructuralsystems,usuallybraced frame,shearwallcoreetc.Inthediagridstructuralsystemstructuralpatternscanbeutilizedtooptimizetheperformanceof structuralmembers.Duetotherapidgrowthofpopulationandincrementoflandvaluesinallaspects,especiallyinurbanand ruralareas,itisthedutyofastructuralengineertocontrivetheversatileperformingstructuralsystems.Asaresult,various structuralsystemshaveeruptedovertheyearsthroughouttheglobe.Theanalysisofdiagridstructureanditsperformance analysisatdifferentangleshasalreadybeenestimatedbysomeresearchers[1,2].Themainvenerationatwhichparticular circumferencetheextendedmaximumstoriesareexploitedanddeflectedindiagridsystemowingtoseismicloading.Butin presentsystemhavepavedthewayfordifferentmethodsofstructuralsystems,therealchallengeslieinprocuringthesystem withhighperformance[3].Wheneverthesoilinhillyregionisstifferorrocky,theinherentbondbetweensoilandfoundation isanemic;thereisadivestingchancetocollapsethestructureagainstearthexcitationinIndia[4,41] Inconventionalbuilding therewillbeallocatednumberofverticalcolumns Butincaseofdiagridverticalcolumnsareputbackbytheinclinedcolumns thatarethediagonals Diagridsarethearrayoftriangleswhichhasthecombinedabilitytoresistgravityandlateralloadsboth inasingleaction[5,41-51].Thediagridstructuresarestiffer,lighterinweightandhavehigherlateralseismicstabilitythan theconventional system [5-9,41-51].Duetothediagonal orhorizontal hollowsupportingmembers and itstriangulated arrangements,thelateralloads,verticalloadsanddistributionsareeasilycountered[6-9].Wearenotproclaimingthatthe extenuation of stories in this structural system at this aberrant and amorphous area against seismic load. Hence, we are lookingforwardforworkingtheversatileseismicanalysis.Diagridisrelativelyanewstructuralsystem,theresearchwork doneoravailableisquitelimited.Themainsourceforanydataavailablefordiagridisformingthediagridbuildingsthathave beenconstructedandthereisonlyhandfuloftheminthewholeworld[14-16].Alargenumberofstudieshavebeenmadeto addresstheissueofvulnerabilityofdiagridsystemunderearthquakeloading[14-18].Eventhroughfewresearchershave extensivelystudiedthisnewsystemandputforththeirfindings,itisnotenoughtoestablishforseismicresponseofthistype ofstructuralsystemwithsecondarybracingsystem[11,21].Theseismicresponseinastructuralsystemisnowessential parameterinrecentdesignmethodology.Generally,symmetricstructuresarefoundtobelessvulnerabletoseismicloadingas compared to asymmetric counterparts. Structures are found to behave symmetrically under lateral loading causes of constraints owing to architectural and functional aspects. From the view of mechanics, symmetric occurs due to the coincidenceofthecenterofmass(CM)andcenterofstiffness(CS).Ineverypartofsectionofstructure,stiffnessiseverywhere sameandmakesamesensebuttheresponseofelementismajordiffered.Ontheotherhand,asymmetricsetbackisanother

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

majorcriteriontodeterminetheseismicexcitationofloadresistingelementofstructurewiththevariationofCMandCS.This eccentricconditionmakesthecriticalresponseduetodifferentparametersthatcreatetheultimateresponseonMDOFsystem Theperformanceanalysisofthediagridstructureisalreadymadebysomeresearchersbuttheliteratureregardingthisina criticalseismiczoneinIndiaisstillunknown.Inthisbackdrop,thiscasestudyreckonstoestimatetheindividualresponsein differentstoriesdiagridstructures.Thestudymayprovideamuchbetterunderstandingofthevulnerabilityofsuchsymmetric diagridsystemalsoforasymmetricsystem.SeveraleminentexamplesofdiagridstructuresinworldhistoryareshowninFig. 1 Dr. Kyoung Moon monitored the dynamic interrelationship between technology and architecture in tall buildings and assignedaninitialsteptowardsfordiagridstructuralsystemin2007.Dr.Lenordstudiedtheeffectofshearleginthediagrid buildingsanddevelopedontheworkdonebyMoonin2005.Researchersconcludedthattheperformanceofstructurethree times than the framed tube building in shear leg ratio and showed higher efficiency in carrying lateral load in high rise buildings[9-13] Differentiatewithconventionalframedtubularstructureswithoutdiagonals,diagridstructuresaremore virtual in minimizing shear deformation because they carry shear by axial action of the diagonal members [17], while conventional framed tubular structures carry shear by the bending of the vertical columns. The diagrid structures have significantly higher resistance against shear lag phenomenon than equivalent tubular structures [18]. Diagrid structure consistingofdiagonalstrutsandtiesintheperipheryandaninteriorcorewithvariouscomplexshape[19,20].Thistypeof structuresispopularinmanydevelopedcountriesintheworldbutinIndiaitisyettogainimportance.Researchershave estimatedtheseismicperformancefactorthatisworthywayforusingpushoveranalysisandIDA-basedprobabilisticapproach comparisonondiagridtall structure.InthatcaseIDA-basedmethodgives significantly morerational valueforreduction coefficient[22,23,47].Very recent researchers scrutinized thathangingontheseismicreliabilityofmultilevel response modificationfactor,forsteeldiagridstructurewheresteelisused30-40%lessthanconventionalstructurethatismoresafety [24-26].Lastbutnottheleast,combinationofshearlinktodissipatetheearthquakeenergywithplasticdesignanalysismodel concludethattheshearlink isexcellentlyperformedandadequatemarginagainstcollapsethatiseffectiveseismic force resistingsystem[27-30,34,39] Significantamountsofworkhavebeendoneinthiscase,buttheapertureindicatesthe judgmental response of diagrid structure due to seismic synthetic bi-directional ground motions excitation, whether the structureofdifferentstoriesforsymmetricandasymmetricsystemswithdifferentdiagonalbracinganglesinacriticalseismic zoneIVinIndia.Moreover,differentparametersareconsideredandlieinafeasiblerangefordiagridresponseintheinelastic range.Itisalsointendedtoinvestigatetheeffectofincorporationofbidirectionalinteractionforbothsystemsintermsof displacementofedgelateralloadresistingelements.Fromthispointofview,wecanstudythedisplacementandstorydrift demandduetoseismicexcitationininelasticresponseforthesatisfactoryofthiseffectivenessincriticalphasethatshouldbe usefulforpracticalanddesignpurposesandisbelievedtobenew.

2. IDEALIZED MODEL STRUCTURES

Inthispaper,modelstructuresarerepresentedforsymmetricsystemsineleven,twenty-oneandthirty-onestoriesofdiagrid structureswithvariousslopes(35°,45°and55°)oftheexternalbracesandalsoaneleven-storyasymmetricsystemwitha55° braceanglerespectively.Theidealizedstructureshavea30m×30mforsquareplanesystemandadiameterof35mfor circular plane systems, as shown in Fig. 2, for preparing the response comparison respectively also 35 m × 40 m for asymmetricplanesystemshowninFig.3isconsidered Theheightofeachflooris3.5m.Inthissystem,rigidfloordiaphragm isconsideredforbothcaseshavingthreedegreeoffreedomthatistwotranslationaldegreeoffreedomalongtwoprincipal directionandonerotationalinplane.Indiagridstructures,apairofbracesarelocatedat6mspacingforcircularmodeland

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

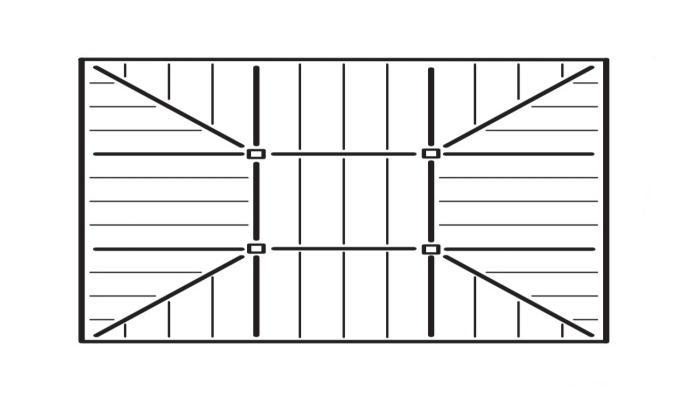
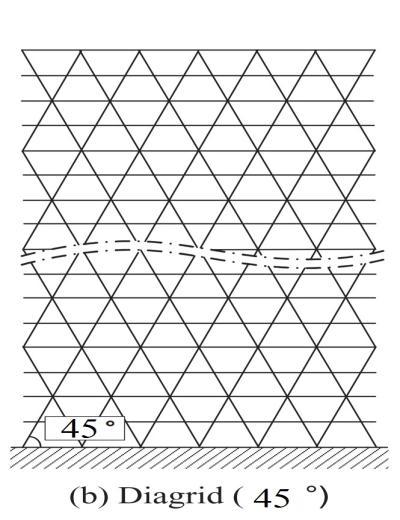
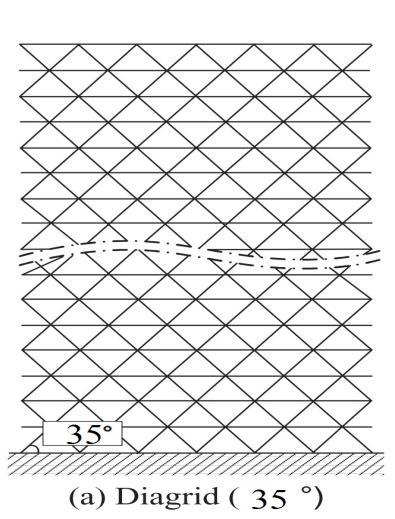
externalcolumnsarespacedat3mfor squareandrectangulardiagridstructurealongtheperimeter. Thegivenmodelis assumedtohavetwolateralloadresistingelementsforbothstructuralsystems forouterandinnersides.Inmidposition, columnissatisfiedasanelementandasanotherelementslaboffloorsisconsidered.Fig.4depictsthesideelevationofthe differentbraceanglesmodelstructures.Theseinclinedmembersi.e.,diagonalbracesareplacedonafixedsupportatearth leveltoheightofstorylevelsthatresisttheshear-bending.Duetoinclinedbracemembers,lateralloadsarecounteredbyaxial exertionofthebracetubes.Theinternalframesaredesignedforgravityloadandthusdispensethepin-jointconnection.

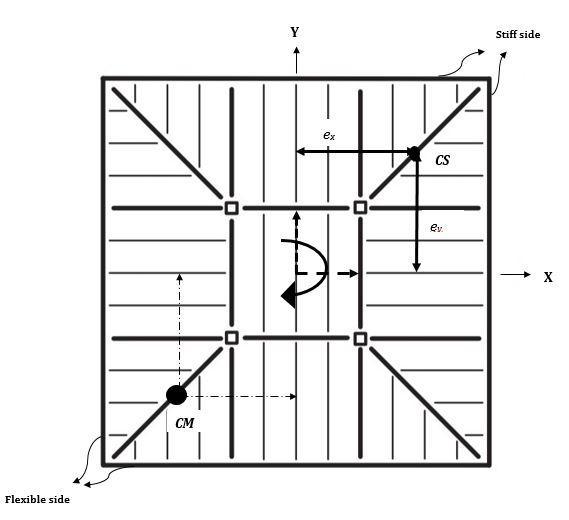
Fig. 2 Planelevationofidealizedsymmetricstructuralsystem

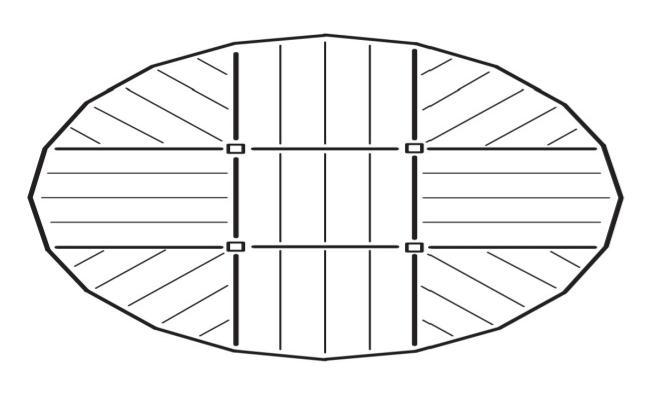
Fig. 3. Planelevationofidealizedasymmetricstructuralsystem.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

Fig. 4 Diagridmodelstructuresfordifferentbracesangle.

Themassofsuchelementsisassumedtobezeroanddenotedbym.Thelateralperiod(Tl),mass(m)andlateralstiffness(k)of allelementsforbothsystemswerecalculatedusingeq.1,Where,mislumpedmassofstory,Kl isthetotallateralstiffness

2/ ll Tmk  [1]

inanyprincipaldirections=4k,kisthestiffnessofelementinanydirectionsforbothcases.Thedegreeoffreedomofrigid diaphragmisvariedwithdifferentrigidfloors.Forthereferencesymmetricsystem,thelocationofCMandCSareinitiallythe same.Besidesthat,keepintouchonthelateralloadresistingedgeelementsofbi-directionallyasymmetricsystemeccentricity isinitiatedbyincreasingthestiffnessofoneedgeelementanddecreasingthatoftheelementattheoppositeedge.Thelateral load-resistingedgeelementswithlessstiffnesswereconsideredlikeflexibleelementsandtheoppositeedgeelementshaving greaterstiffnesswererepresentedtoasstiffelements.Inthissystem,thelocationoftheCMandCSreclineatthedifferent eccentric location and assume on a same axial section. In such bi-directionally asymmetric systems eccentricities are symbolizedbyex andey thatliesbetweenthedistanceofCMandCSwithrespecttoprincipalaxisofsystem.Distributionof eccentricconditionisbalancedforbotheccentricities’ex andey with the positivesensewhereCS andCM liesin thefirst quadrant.Anotherobservationshowsthatthenegativeeccentricsensethatisex and-ey whereCMandCSliesinthesecond quadrantoftheprincipalaxisofthesystem.Suchthisstudygivesanideaaboutthenatureofeccentricitymakesanydifference ornotinthebehavior.Thestiffnessandmassofallfloorsindifferentstoriesisvaried,wheremassofdifferentfloorsgenerated byseveralparameters.Arangeofsymmetricandasymmetricsystemswithanotherwisesamefundamentalparameterhas beenstudied.

3. METHODOLOGY

Thenon-linearequationofmotionshowineq.2.isnumericallysolvedintimedomainusingNewmark’sβ-γmethodandbythe bymodifiedNewton-Raphsontechniqueisusedforiteration.TheNewmark’sparametersarechosenasγ=0.5andβ=0.25 [31,33,37-40].TheresultsarecomputedwithvarioussizesoftimestepgivenbyTx/N,whereTx istheuncoupledlateral periodandNisanintegernumberwhichisgraduallyincreasedbydoublingittoobtaintheresultswithbetteraccuracy.For thispurpose,weconsideredtimestepofTx/400forappropriatedeterminationofvalues[31,33,37].SeismosignalV.5.1.0–A computerprogramthatconstitutesaneasyandefficientwayforsignalprocessingofstrong-motiondata[online];2018,ed: availablefromURL:(http://www.seismosoft.com)andbythebyaddedtheessentialparametersthatismomentmagnitude, closestsite-to-fault-rapturedistance,shearwavevelocity,meantimeperiod[32] Usingthisessentialsoftwareinvestigating theultimatecharacteristicofgroundaccelerationmotioncapacitythathasbeenactedonthestructuraldiagridmembersas wellasthedifferentangleofbracesthatliesinjointconnection.Where,ristheradiusofgyrationofmassofrigiddeck;cisthe dampingmatrix;ux,uy,θarethetranslationsofCMalongthexandyaxisandrotationofCMishorizontalplanerespectively andügx andügy aregroundaccelerationsalongtwoperpendicularprincipalaxesrespectively.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

4. GROUND MOTION

For the diagrid structural model an enhanced nonlinear dynamic analysis has been used which is capable to capture progressiveseismicdamageofstructures.Asscalednear-fault(NF)groundmotionsareconsideredfromPacificEarthquake EngineeringResearch(http://peer.berkeley.edu)Centerfortheperformanceanalysis[37].Thegroundmotionisgeneratedon astructuralsystemlikeavectorformation,oftenorientedinnorth-south(N-S)andeast-west(E-W)directionswhereasthe strongmotiondatabaseforhorizontalcomponentsofmotionsaregenerallyavailablealongorientationsofrecordingwhichare oftenarbitrary.Thisrecordedcomponentisappliedalongtwoprincipalaxesofthestructurewiththeshearingbraceeffect. Thus,itisoftendeducedthatthearbitrarilyplacedrecordingsensorsarealignedwiththeprincipalaxesofstructure.Inthis way,overallstructuralresponseoftheMDOFdiagridsystemisestimatedowingtobi-directionalNFsyntheticgroundmotion historyundercriticalzoneIV.Thecasestudiesinthispaperareinvestigatedforasetoffifteenbi-directionalsyntheticground motionstoresistanyvariabilityarisingsubjectedtotheparticularcharacteristicofanyspecificgroundmotion.Detailsofthe groundmotionsareshowninTable1.Weselectgroundmotionsintermsofgeophysicalparameters,viz.,magnitude-distancesoilconditionstriads.Selectedmotionsarescaledappropriatelytointroduceauniformlevel ofinelasticaction.Foreach componentofamotion,thisscalefactorisdecidedobservingthespectralaccelerationofeachoriginalrecordcomponentatthe fundamentalperiodofvibrationofelementinrelationtotheelementcapacity.Scalefactorsoftwocomponentsofarecordso computedarecomparedandtheaveragefactorisappliedtothecomponents.

Table 1: Detailsofgroundmotions(NF)used.

Serial no. Event (Year) Station Record ID Moment magnitude (Mw) r(km) Vs30(m/s) PGA(m/s2) Tm(s) XComponent YComponent X -Direction Y- Direction

1 Corinth_ Greece, 1981 Corinth RSN313 6.6 10.27 361.4 2.32 2.90 0.17 0.14

2 Landers, 1992 JoshuaTree RSN864 7.3 11.03 379.32 2.68 2.78 0.73 0.78

3 Landers, 1992 Morongo ValleyFire Station RSN881 7.3 17.36 396.41 2.19 1.61 0.69 0.88

4 Manjil_ Iran,1990 Abbar RSN1633 7.4 12.55 723.95 5.04 4.87 0.32 0.33

5. Tottori_ Japan,2000 OKY004 RSN3907 6.7 19.72 475.8 8.08 5.28 0.20 0.18

6 Chuetsu-oki_ Japan,2007 Yoshikawak uJoetsuCity RSN4850 6.8 16.86 561.59 4.44 3.08 0.79 0.83

7. Iwate_ Japan,2008 MYG005 RSN5664 6.9 13.47 361.24 5.25 4.37 0.78 1.76

8 Iwate_ Japan,2008 Kurihara City RSN5818 6.9 12.85 512.26 6.89 4.14 0.39 0.42

9 Chichi_Taiwan03_1999

TCU129 RSN1023 6.2 10.9 511 9.85 6.12 0.35 0.34

10 Imperial valley-1979 Elcentro Array#4 RSN179 6.5 7.1 209 4.75 3.63 0.68 1.29

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

11 Imperial valley06_1979

Elcentro Array#6 RSN181 6.5 1.4 203 5.19 3.76 0.66 1.22

12 Imperial valley06_1979 Elcentro Array#10 RSN173 6.5 8.6 203 5.19 3.76 0.66 1.22

13 Kocaeli, Turkey_1999 Duzce RSN1158 7.5 13.5 282 3.06 3.57 0.87 0.50

14 Loma Prieta_1989

LosGatosLexington Dam RSN3548 6.9 5.5 1070 4.34 4.04 0.89 0.98

15 Denali, Alaska_2002 TAPSPump Station#10 RSN2114 7.9 2.7 329 3.26 2.92 1.52 1.19

5. SYSTEM PARAMETERS

The variation of maximum displacement response may be influenced by several system parameters as well as loading considerationsforvaluableconclusions.Theseprimarilyconsiderabletwodynamiccontrolparametersnamelythelateral naturalperiod(Tx)andtheuncoupledtorsional-to-lateralperiodratio(τ).Thislateralperiods(Tx)consideredforsymmetric systemsliesbetween0.25to2.0secandforasymmetricsystemitconsidered0.25sec,0.5sec,1.0secand2.0secinshort, mediumandlongperiodrangesrespectively.Ontheotherhand,formostrealbuildings,thevaluesofuncoupledtorsional-tolateralperiodratio(τ)arevariedwithintherangeof0.25-2.0withanintervalof0.05alsousedinpreviousresearch[31,33, 37].Influencethetorsionaleffectforasymmetricsystemeccentricityisimportantcriteriatoobservethecriticalresponseof structuralelementswithrespectonτ.Further,thepresentstudyattemptstoincorporatetheanalysisofthebi-directional asymmetricsystemintoafeasiblerangeofeccentricvariation.Inthiscasestudy,thethreetypicaleccentricparametersofthis systemareclassifiedintermsofsmall,intermediateandlargeeccentricsystemsasrepresentedase/D=0.05,0.1and0.2used inpreviousliterature[33,37].Hence,sixcombinationsofeccentricityareconsideredalongtwoprincipaldirectionsinthis paper,aslistedinTable2. Asymmetricsystemswithstiffnessandmasseccentricitiesareconsideredinthispresentstudy.The fourdifferentvaluesofductilityreductionfactor(Rµ)=2,4and6arechosenonlyforsymmetricstructurewhereasstandard reductionfactorRµ=4selectforasymmetricsystemonly.Thesevaluesarehighlyrecommendedbythedifferentcodes,suchas ASCE7-05[36]andNEHRP[35].

Table 2: Combinationsofeccentricityconsideredalongtwoprincipaldirections.

Sl. No. ex/D ey/D 1. 005 01 2. 005 02 3. 0.05 0.05 4. 02 02 5. 01 01 6. 01 02

Note: ex andey areeccentricityinxandy-axisrespectively.

6. RESULTS AND DISCUSSION

Thenonlineardynamicanalysisofdifferentstorydiagridstructuresthatareelevenstory,twenty-onestoryandthirty-one story systems through mean element displacement (for Rμ=2, 4 and 6) for various angle of braces (35°, 45° and 55°) is presentedwithplottingasrepresentativeofthetrendforbothcaseswiththetimevariationliesbetweensmalltolargelateral periodthatis0.25secto2.0secforsymmetricsystem Fig.[5-7]showsthemeandisplacementforvariousmodelstructurein differentstoryatsmall,intermediateandlargebraceanglesobtainedbynonlineardynamicanalysisforsquarediagridplan

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

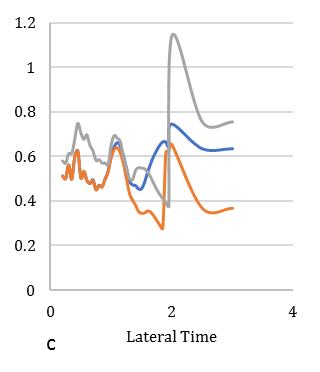
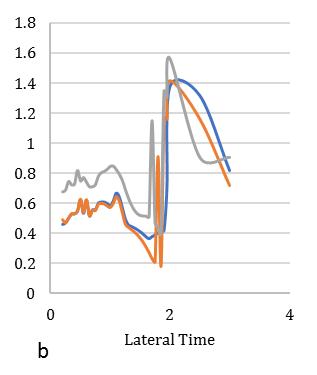
sectionandaswellasanotherpartshowinFig.[8-10]fortubetypeanalysismodelstructurewithacircularplanshape.Fig.[5] indicatestheamplificationinresponseforsquaresymmetricconfigurationmaybe1.8,1.5and1.1times,whereas,forcircular section response indicates 1.5, 1.3, and 0.9 times respectively for Rμ=2 show in Fig. [8] Influence of ground motion characteristicsonthenonlineardynamicseismicresponseofsymmetricdiagridstructuralsystemissystematicallyexamined toachieveafairinsightintothebehaviorofsuchsystems.Fig.[6]indicatestheamplificationinresponseforsquaresymmetric configurationmaybe2.6,2.3and2.1times,whereas,forcircularsectionresponseindicates2.3,1.9,and1.6timesrespectively forRμ=4showinFig.[9].Fig.[7]indicatestheamplificationinresponseforsquaresymmetricconfigurationmaybe4.2,3.9 and3.5times,whereas,forcircularsectionresponseindicates3.8,3.6,and3.4timesrespectivelyforRμ=6showinFig.[10]. Fig.[5]andFig.[8]revealthattheincreaseindisplacementresponse0.35,0.31,and0.2timesforbi-directionalexcitationfor Rμ=2.Fig.[6]andFig.[9]revealthattheincreaseindisplacementresponse0.42,0.4,and0.5timesforbi-directionalexcitation forRμ=4,wheretorsionaltolateralperiodratio(τ)isnegligibleforzeroeccentriccondition.Finally,Fig.[7]andFig.[10]reveal thattheincreaseindisplacementresponse0.41,0.32,and0.1timesforbi-directionalexcitationforRμ=6.

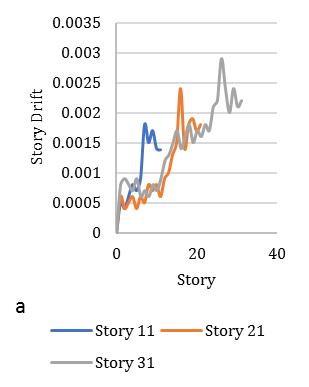
Ontheotherscenario,storydriftoneofthesignificantcriteriafortheassessmentindriftdemandofdifferentstorybuildings undergroundmotionsexcitationarepresentedinFig.[11]forsquarediagridsystemandFig.[12]representedforcircular diagridstructuralsystem.Fig.[11]indicatestheresponseofdriftdemandforsquaresymmetricconfigurationmaybe0.0032, 0.0026and0.0024times,whereasforcircularsectionresponseindicates0.0029,0.0023,and0.002timesrespectivelyshowin Fig.[12].Inthiscase,structuresarerevealedthattheincreaseindriftdemand0.0005,0.0003and0.0004timesforbothcase

studies.Itcanbeobservedthatastheslopeofthebracesincreases,themeanvalueofthemaximumdriftalsodecreasesthatis alsosatisfactoryfordisplacementdemand.Inthestructureswithbraceslopeofa35°and45°,thedisplacementandmaximum driftsdemandinthehigherfewstoriesaresignificantlylargerduetotheparticipationofthehighermodeeffectsforbothcase studies.Driftdemandisbeingmaximumattopstoryifthediagridinclinationangleisbeingminimum.Furthermore,drift demandinintermediatestoryisbeingmaximumforminimumdiagridangle,whereasinlowstoryitvariesshowinFig.[1112].Ontheotherscenario,meanofnormalizedresponsearecomputedandpresentedforcornerelementsaremorevulnerable

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

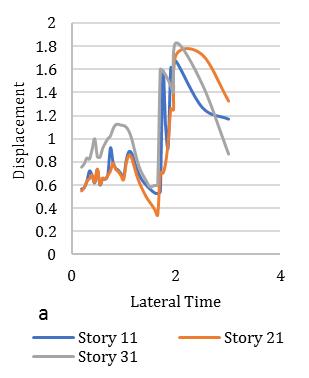
Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

Fig. 6. Meandisplacementresponseofsquarediagridsystemfor(a)35°,(b)45°,(c)55°braceangles(Rµ =4).

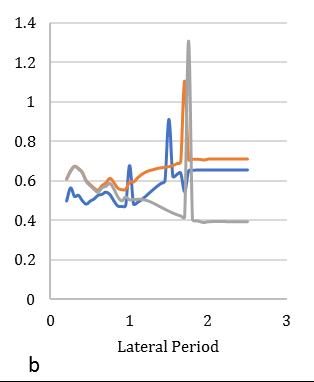
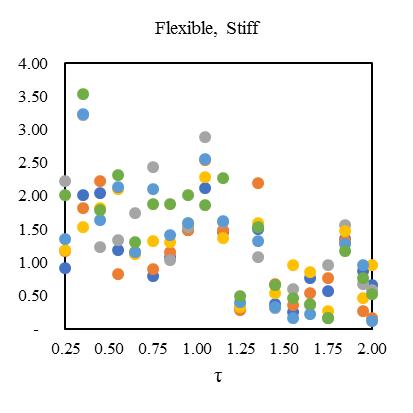
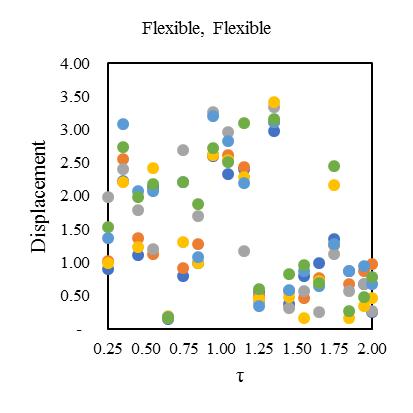
duetolateralandtorsionalcouplingeffectinasymmetricstructure.ThesecornerfourelementsElement1isflexiblealongboth principal directions and designated as “flexible, flexible”. Element 2 and Element 4 are combined as flexible and stiff for differentprincipalaxis,designatedas“flexible,stiff”and“stiff,flexible”respectively.Element3isstiffalongbothprincipal directionandfinallydesignatedas“stiff,stiff”.Theresponseofallcornerelementsaredevelopedforphysicalunderstanding duetobi-directionalsystemofasymmetry.Theconsidarablelateralperiodsforsmall,mediumandlargetimehistoryclearly

Fig. 7. Meandisplacementresponseofsquarediagridsystemfor(a)35°,(b)45°,(c)55°braceangles(Rµ =6).

Fig. 8. Meandisplacementresponseofcirculardiagridsystemfor(a)35°,(b)45°,(c)55°braceangles(Rµ =2).

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

Fig. 9. Meandisplacementresponseofcirculardiagridsystemfor(a)35°,(b)45°,(c)55°braceangles(Rµ =4).

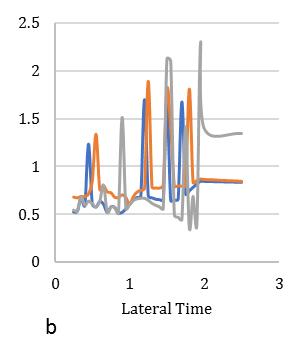
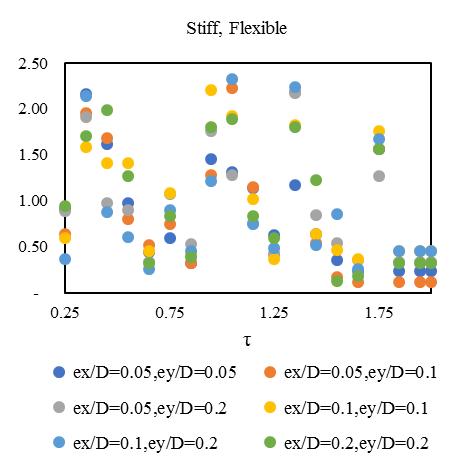
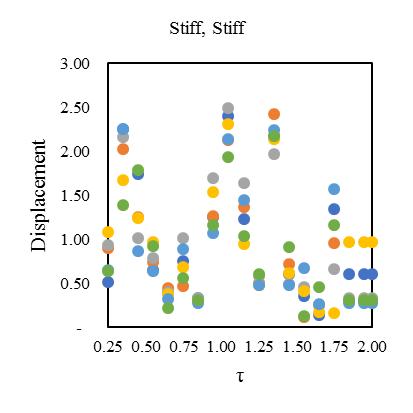
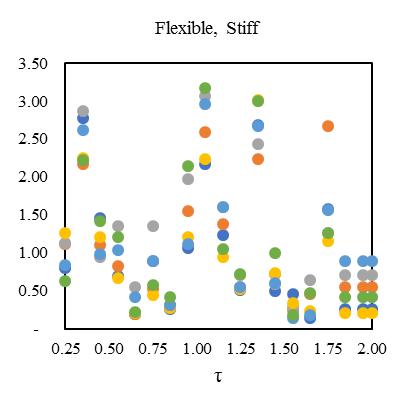
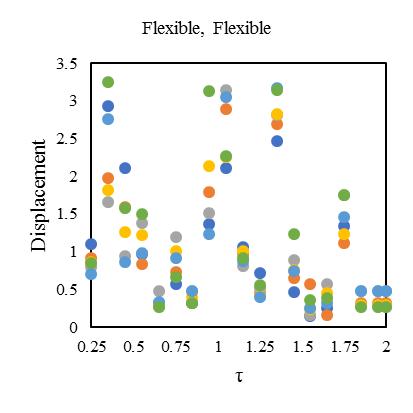
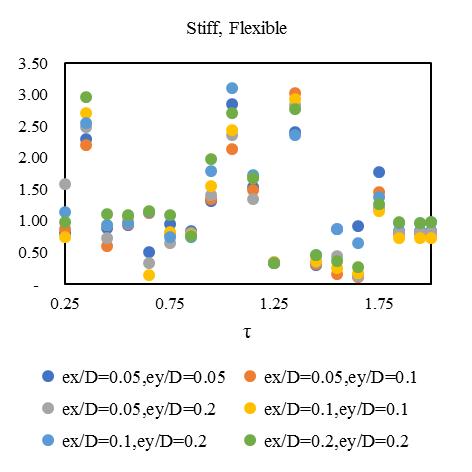
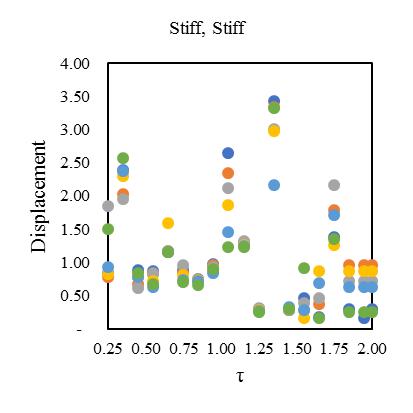
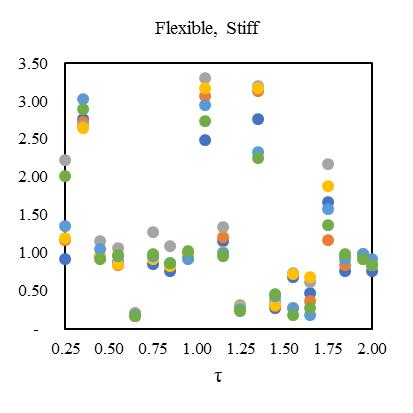
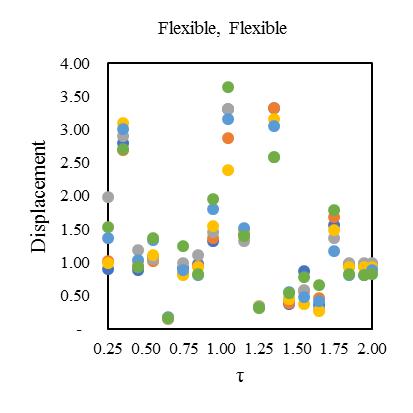
plottedinFig.[13-16]alsodependentonductilityreductionfactor(Rμ)=4forobtainingthecriticalinelasticresponseinzone IVat55°standardbraceangle.Fig,[13-16]hasfoursetsofgraphsshowsthemeanofresponseforadifferentcombinationof bi-directionaleccentricsystem.Inthesehybridsteel-concretestructuralmodelindicatesthedynamicresponseupto2to3.1 timesfor0.25sec,2.3to3.2timesfor0.5sec,2.9to3.5timesfor1sec,3.1to3.65timesfor2secrespecttotorsionaleffectand

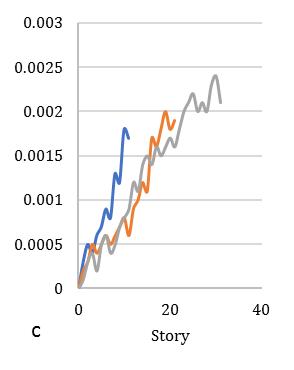
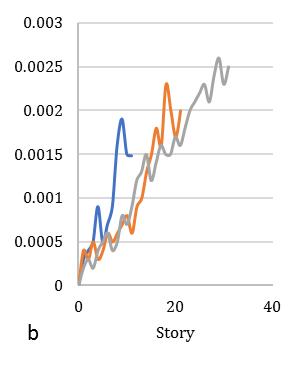
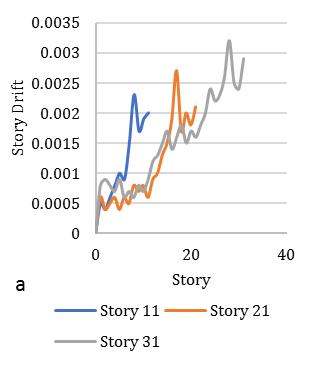
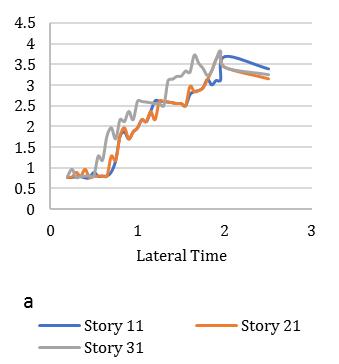
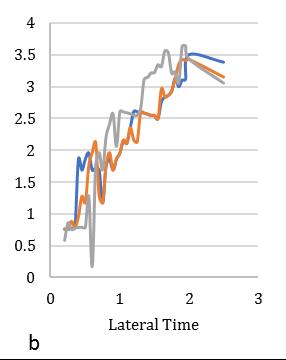
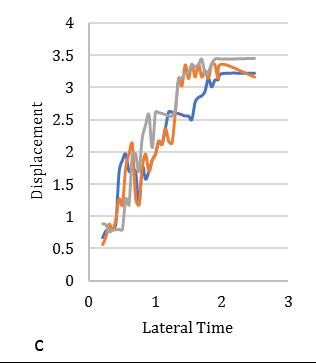
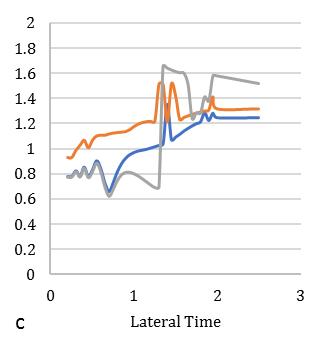
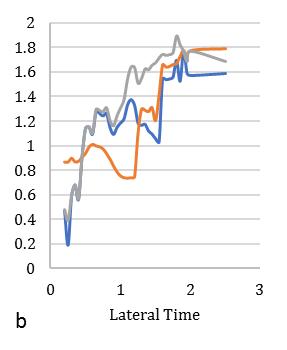
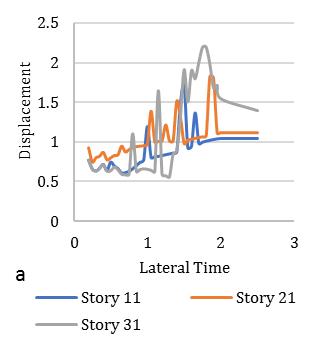
Fig. 10. Meandisplacementresponseofcirculardiagridsystemfor(a)35°,(b)45°,(c)55°braceangles(Rµ =6).

Fig. 11. Driftdemandofsquarediagridsystemfor(a)35°,(b)45°,(c)55°braceangles.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

Fig. 12. Driftdemandofcirculardiagridsystemfor(a)35°,(b)45°,(c)55°braceangles.

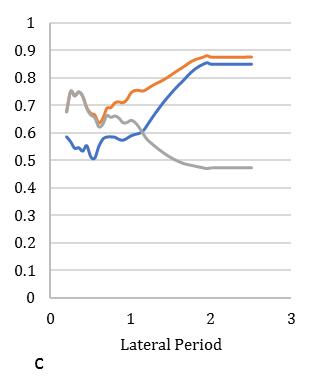
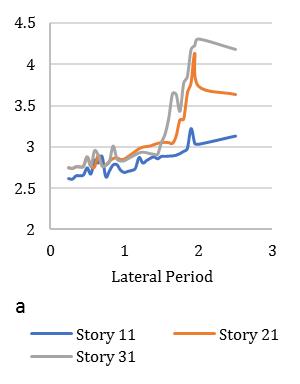
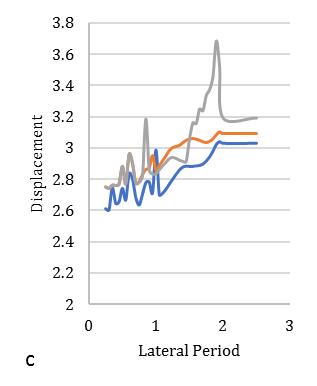
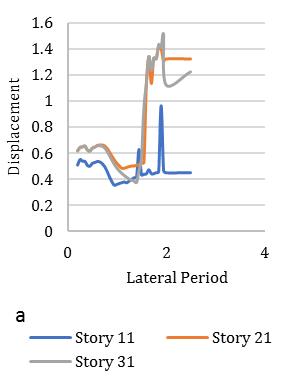
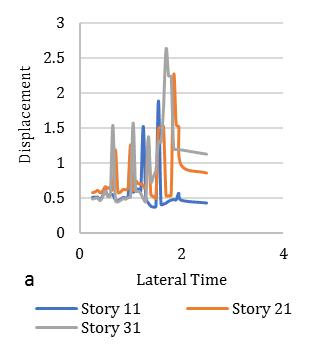
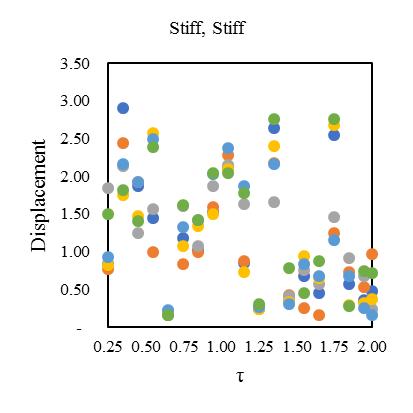
variationofstiffness-masseccentriccondition.Consideringlateralperiod0.25sec,the1stElementmaximumdeformationlies 3.1timesandminimum2timesfor3rd Element.Inthatcase,Element2and4carriesthealmostsameresponsethatlies

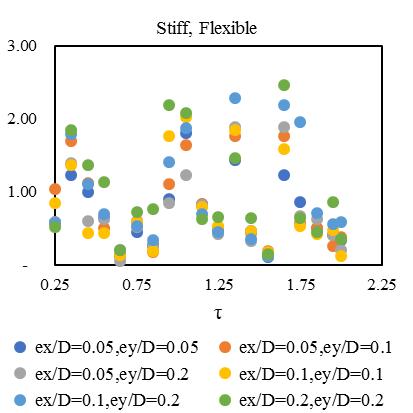
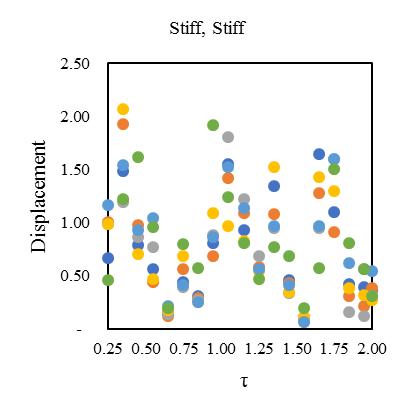
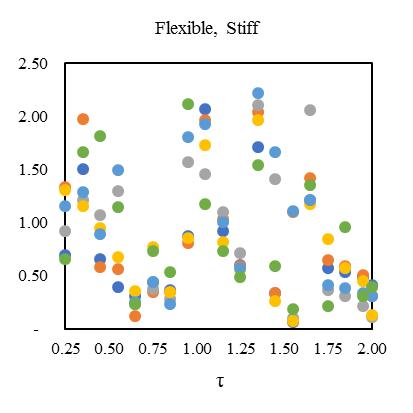
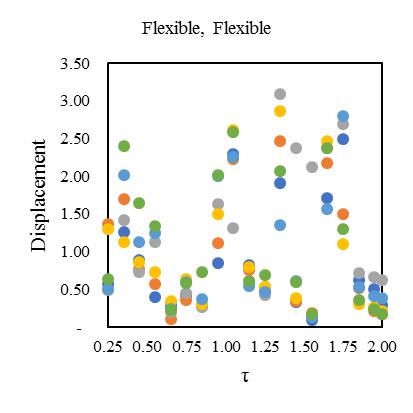
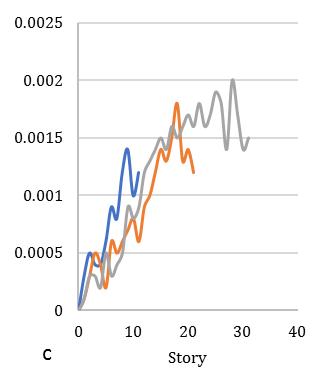
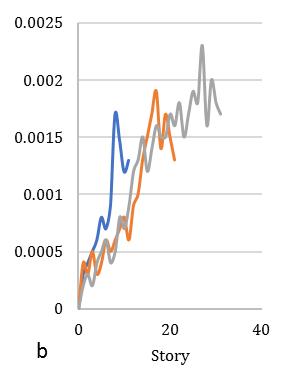
Fig. 13. MeandisplacementresponseofasymmetricdiagridsystemforT=0.25secat55°braceangle(Rµ =4).

2020, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

Fig. 14 MeandisplacementresponseofasymmetricdiagridsystemforT=0.5secat55°braceangle(Rμ=4).

2020, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

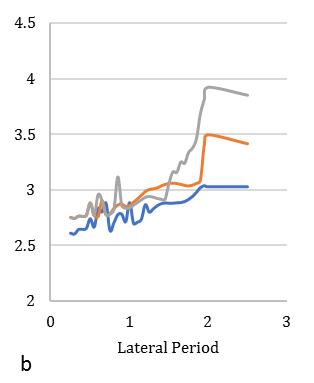
Fig. 15. MeandisplacementresponseofasymmetricdiagridsystemforT=1.0secat55°braceangle(Rμ=4).

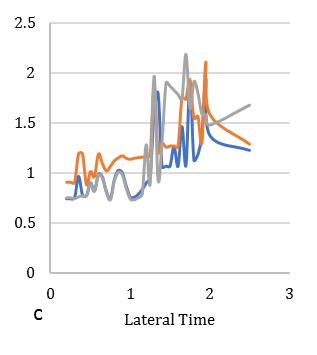
Fig. 16 MeandisplacementresponseofasymmetricdiagridsystemforT=2.0secat55°braceangle(Rμ=4). © 2020, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page434

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

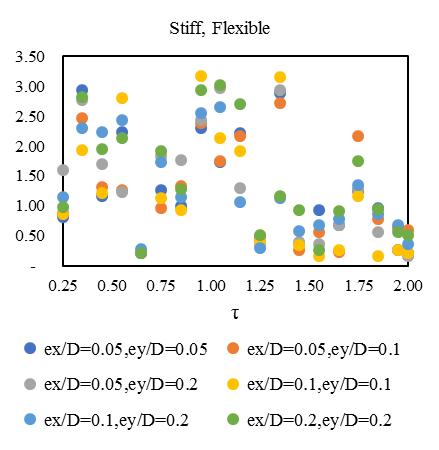
between2.2-2.4showninFig.[13].Furthermore,consideringlateralperiod0.5sec,theElement1liesmaximumdeformationat 3.2timesandminimum2.3timesforElement4.Element2and3carriestheaverageinelasticdemandliesbetween2.5-3.1 showninFig.[14].Forlateraltime1sec,theelement2liesmaximumdeformationat3.5timesandminimum2.9timesfor Element3.Element1and4obtainthedemandliesbetween3.2-3.4timesshowninFig.[15].Fig.[16]showsthemaximum Element1deformationfor3.65timeswhereasminimumcarriedoutforElement4at3.1times.Element2and3showsthe displacementbetween3.3-3.4timesthatnearaboutsame.Inthiscontext,itisneededtoobservefrom15earthquakedatathat is plotted for two different extreme combinations of eccentricities along X and Y directions. However, in this point, the observationforinelasticseismicresponseofasymmetricdiagridsysteminsmalltolargecombinationofdifferenteccentric conditionsthatassembleaneffectivescenarioinseismiczoneIVforsuitability.

7. CONCLUSIONS

Thepresentinvestigationanalyzestheinelasticseismicperformanceofdifferentstorydiagridsymmetricandasymmetric modelplanstructureswithvariousangleofbracesareevaluatedundercriticalseismiczoneIVinIndiaowingtobi-directional NFgroundexcitation Theresultsarealsoindicatedtocomparetheperformancewithsquareplandiagridstructurestocircular modelplandiagridstructuresforthesuitabilityincriticalseismiczoneIVinIndia.Also,theasymmetricsystemshavebeen attemptedtheperformanceanalysisforbetterunderstandingofserviceability.Thefollowingbroadconclusionsemerge.

1. Thestrongvulnerabilityofgridstructuralloadresistingelementsduetothebi-directionalgroundmotionclearly showsthattheelementsarelessamountoflossesonlateralperiodsthanR/Cstructuralsystem.Theresponseof structuresforbothcasestudiesindicatethatthehigheroverstrengthwithsmallerductility,dependsoncriticalangle ofbraces.Further,theseismicdemandofelementsappearstovaryirregularly,asaresultthestorywisevariationof bothsystemsvariessimilarly.Inthisstudy,dynamicobservationappearstobemoreimportantfromtheviewpointof mechanics.

2. Consideration of symmetric configuration effect owing to simultaneous bidirectional shaking may produce the inelasticdemand. Theresultanalysisimpliesforbothcasesamplifiestheresponseconsiderably. Thestructural deformationofthesquarediagridsystemishigherthancircularsystemwithrespecttothelateralperiods.Onthe otherhand,storydriftdemandclearlydemonstratesthatthehigherdemandingvalues,significantlyscatterrandomly onhigherstorylevelthanlowerstory.Inthatcase,driftdemandismaximumforsquaresystemthatinfluencesthe inelasticresponseofhighermodaleffect.Thebird’seyeobservationrepresentstheperformanceofcircularsystemis betterthansquaresystemduetogroundexcitation.

3. Thediagridstructurewiththebraceanglebetween50°to60°seemsthatitisresistingtobemoreefficientwithlateral loadsaswellasgravitationaleasilyinzoneIV.Also,itisdemonstratedthatthisstandardbraceangleissuitablefor anyasymmetricsystem.Braceanglebetween40°-50°isacceptableforsquareandcircularsystemsthatcontrolsthe largenumberofdeformationanddriftdemand InthisdiagridstructuralsystemM25gradeofconcreteissuitablefor lightweightofelementsandalsosteelgridsectionispreferablewithpin-jointconnectionforflexibilitythanconcrete gridjointconnection

4. Considerationofbi-directionalinteractionforasymmetricdiagridsystemmayproducehigherinelasticdemand.With increasingtheuncoupledlateralperiodofstructure,decreasingtheinelasticrangeforsuchflexiblesystemsandlies constant. The response of asymmetric system at 55° brace angle lucidly concludes that the response due to bidirectionalgroundmotionobtainsamajoreffectivenessofloadresistingelementsunderthevariationofeccentric conditionsinzoneIV.Theelementaldeformationforlargebraceangleliesbetween50°-60°considerassuitablefor zoneIV,relaxingmodaleffectinrandomvibration.

Thus,thepresentpapermaybehelpfulintheprocessofresponseanalysisofthebuiltorto-be-builtstructuresintheeventof any anticipated earthquake prone and believe to be new. Safety level of the structures are undergoing seismic excitation withoutcollapsemaybeassessedtoplanforthepost-earthquakestrategy.Suchasymmetricandasymmetricdiagridplan structuresservevariousfunctionalandarchitecturalrequirements duetoplanandinterconnectionactivitiesleadstothe additionalvulnerabilityofsystem.Furthermore,thesensitivityofthebi-directionallyattackingforcesexecutetheseismic deteriorationofsuchsystems.Thispresentpapermayproveusefultoprovidebroadguidelinestoaddressallessentialissues and to highlight the needs for investigating the same in further details. These results can, therefore, help to evaluate the retrofittingassessmentduetoadditionalstrengthdemand.Thesefindingspointoutthelimitationofcurrentcodesdeveloped primarily on research in this particular aspect that employed a multi-story model. Hence, this interesting study may be extendedtoassessthesoil-structureinteractioneffectforasymmetricdiagridstructuralsystemobtainingfurtherinsight.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

REFERENCES

[1] KhalidK. Shadhan“Optimaldiagridangletominimizedriftinhigh-risesteelbuildingssubjectedtowindloads”,IJCIET, Vol.06,2015.

[2] V. R.Nishith,B. Panchal,Dr. Patel,Dr.I. I. Pandya,“OptimumAngleofDiagridStructuralSystem”,IETR,Vol.02,Issue: 06,2014.

[3] Sachin,PradeepA. R.,SANJITHJ.,L. S. Kumar,“PushoverAnalysisofCircularSteelDiagridStructures”,IRJET,Vol.03, Issue:06,2016.

[4] V.Baile,Dr.A.A.Bage,“ComparativeStudyofDiagrid,SimeFrameandVariousBracingSystems”,IJIRSET,Vol.06,Issue. 06,2017.

[5] B. Shankar,D.K.,S. N. Hijaz,“StudyonbehaviorofDiagridsunderSeismicloadscomparedtoConventionalmoment resistingframes”,IRJET,Vol.04,Issue:08,2017.

[6] PavanaV.,Dr.S. Desai,“PerformanceAnalysisofTallStructurewithDiagridforSeismicloads”,IRJET,Vol.04,Issue:08, 2017.

[7] A. V. Gorle,S. D. Gowardhan,“OptimumPerformanceofDiagridStructure”,IJER,Vol.05,Issue:03,2016.

[8] N. B. Panchal,V. R. Patel,“Diagridstructuralsystem:StratehiestoReduceLateralForcesonHigh-RiseBuildings”,IJRET, Vol.03,Issue:04,2014.

[9] P. UdayKumar,Supreeth.S.,PradeepC. R.,“StudyonbehaviorofTubularDiagridstructuresduringSeismicexcitation”, IRJET,Vol.04,Issue:06,2017.

[10] K. S. Moon,“StructuralDesignandConstructionofComplex-ShapedTallBuildings”,IJET,Vol.07,2015.

[11] D. N. Sorathiya,J. Gadhiya,A.Raturi,“ReviewonbehaviorofDiagridStructuralsysteminHigh-RiseBuilding”,Vol.02, Issue:11,2017.

[12] L. Mohan,C. K. P. Thampan,”NumericalModelingandEvaluationofHybridDiagridStructures”,IJRAT,2015.

[13] R. D. Deshpande,S. M. Patil,S. Ratan,“AnalysisandComparisonofDiagridandConventionalStructuralSystem”,Vol. 02,Issue:03,2015.

[14] Joshi.R. S.,Dhyani.D. J.,“AReviewonNovelStructuralDevelopmentinTallBuilding:DiagridStructure”,IJAER,2017.

[15] G. Dethe,M. Banagar,P. Kenjale,A. Das,M. Dusane,K. Prajapati,“AnalysisofDiagridStructure”,IRJET,Vol.05,Issue: 03,2018.

[16] KumarV.,H.S.Vidyadhar,“Analysisof3DRCframeonslopingground”,IRJET,Vol.04,Issue:09,2007.

[17] MoonK.S.,“Diagridstructuralsystemsfortallbuildings,characteristicsandmethodologyforpreliminarydesign”,The StructuralDesignofTallandSpecialBuildings,Vol.16(16),2007.

[18] KimJ.,LeeY.H.,“Progressivecollapseresistingcapacityoftube-typestructures”,TheStructuralDesignofTalland SpecialBuildings,2009.

[19] MoonK.S.,“Diagridstructuresforcomplex-shapedtallbuildings”,ProcediaEngineering,Vol.14,2011.

[20] MoonK.S.,“Optimalgridgeometryofdiagridstructuresfortallbuildings”,ArchitecturalScience,Vol.51(3),2008.

[21] Montuori G. M., Mele E., Luca A. DE., Brandonisio G., “Secondary bracing systems for diagrid structures in tall buildings”,Engineeringstructure,Vol.75,2014.

[22] Seyedkazemi A., Roffoei F. R., “Comparison of static pushover analysis and IDA-based probabilistic methods in assessingtheseismicperformancefactorsofdiagridstructures”,ScientiaIranica,2019.

2020, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

[23] RofooeiF.R.,SeyedkazemiA.,“Evaluationoftheseismicperformancefactorsforsteeldiagridstructuralsystemsusing FEMAP-695andATC-19procedures”,BulletinofEarthquakeEngineering,2020.

[24] Mogsenian V., Padashpour S., Hajirasouliha I., “Seismic reliability analysis and estimation of multilevel response modificationfactorsforsteeldiagridsystem”,JournalofBuildingEngineering,Vol.29,2020.

[25] MogsenianV.,GharaeiN.,“Reliabilityanalysisandmulti-levelresponsemodificationfactorsforbucklingrestrained bracedframes”,JournalofConstructionalSteelResearch,Vol.171,2020.

[26] Scaramozzino D., Lacidogna G., Carpinteri A., “New trends towards enhanced structural efficiency and aesthetic potentialintallbuildings:Thecaseofdiagrids”,AppliedSciences,Vol.10(11),2020.

[27] TianxiangLi.,YangT.Y.,TongG.,“Performance-basedplasticdesignandcollapseassessmentofdiagridstructurefused withshearlink”,TheStructuralDesignofTallandSpecialBuildings,Vol.28(6),2019.

[28] ZahiZ.,GuoW.,Y.Li.,Yu.Z.,CoaH.,BuD.,“Animprovedperformance-basedplasticdesignmethodforseismicresilient fusedhigh-risebuildings”,EngineeringStructures,Vol.199,2019.

[29] EsteghamatiM.Z.,FarzampourA.,“Probabilisticseismicperformanceandlossevolutionofamulti-storysteelbuilding equippedwithbutterfly-shapedfuses”,JournalofConstructionSteelResearch,Vol.172,2020.

[30] ChengQ.,SuM.,LianM.,“Cyclicbehaviourofhigh-strengthsteelframed-tubestructureswithboltedreplaceableshear links”,EngineeringStructures,Vol.210,2020.

[31] DuttaS.C.,DasP.,“Validityandapplicabilityoftwosimplehysteresismodelstoassessprogressiveseismicdamagein R/Casymmetricbuildings”,JournalofSoundandVibration,Vol.257(4),2002.

[32] SeismosignalV.5.1.0–Acomputerprogramthatconstitutesaneasyandefficientwayforsignalprocessingofstrongmotiondata[online];2018,ed:availablefromURL:(http://www.seismosoft.com)

[33] DuttaS.C.,HussainA.M.,“Inelasticseismicbehaviourofasymmetricstructuresunderbidirectionalgroundmotion:An efforttoincorporatetheeffectofbidirectionalinteractioninloadresistingelements”,Structures,Vol.25,2020

[34] HeshmatiM.,KhatamiA.,ShakibH.,“Seismicperformanceassessmentoftubulardiagridstructureswithvaryingangles intallsteelbuildings”,Structures,Vol.25,2020.

[35] NEHRPRecommendedProvisionsforSeismicRegulationsforNewBuildingsandOtherStructures(FEMA450),2006

[36] ASCE/SEI7-05.MinimumDesignLoadsforBuildingsandOtherStructures,2013.

[37] ChowdhuryK.,ChowdhuryU.,HazraA.,“InfluenceofangleofincidenceininelasticresponseofanidealizedsinglestoryR/Cstructuralsystemduetobi-directionalgroundmotion”,IRJET,Vol.8(9),pp.915-937,2021.

[38] RoyS.,ChowdhuryK.,HazraA.,“StudyonthebehaviorofsinglestoriedR/Cframedstructureunderblastloadingand seismicexcitation”,IRJET,Vol.7(9),pp.522-534,2020.

[39] ChowdhuryK.,RoyU.S.,BairagiG.,“Assessingtheseismicresponseofmulti-storyasymmetricstructuralsystemin zoneIVusingextendedN2method”,IRJET,Vol.7(6),pp.4700-4706,2020

[40] ChowdhuryU.,ChowdhuryK.,BairagiG.,“Assessmenttheaccurateresponseofembeddedpileinlayeredearthwith differentmethodofanalysis”,IRJET,Vol.7(7),pp.20-25,2020.

[41] SinakiF.G.,MoghadamA.S.,“Comparisonofseismicbehaviorofbuildingswithdiagridstructureinrockingmotion andmomentframestructureconsideringsoil-structureinteraction”,BulletinEarthquakeScienceandEngineering,Vol. 9(1),pp.43-61,2022.

[42] LodhiD.S.,ShekhawatS.S.,“Seismicanalysisandcomparisonofdiagridbuildingwithflatslabanddiagridbuilding withoutflatslabwithconventionalbuilding”,IRJMETS,Vol.4(3),pp.119-125,2022.

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056

Volume: 9 Issue: 11 | Nov 2022 www.irjet.net p-ISSN: 2395-0072

[43] Sindhu N. S., Anandh S., Anas A. M., “A comparative study on seismic analysis of diagrid and hexagrid structural system”,IOPConferenceSeries:MaterialsScienceandEngineering,Vol.1130(1),2021.

[44] WaniS.S.,KokateP.G.,LondheA.S.,MalgeS.B.,PotdarA.N.,“Comparativeanalysisofdiagridstructuralsystem”, IJCEAE,Vol.3(1),pp.33-40,2022.

[45] Babhulkar S., Dabhekar K. R., Sanghani S. S., “Comparative study of seismic behavior of diagrid structure with conventionalstructure”,IOPConferenceSeries:MaterialsScienceandEngineering,Vol.1197(1),pp.1-8,2021.

[46] RahulC.LokeshJ.K.,“Seismicbehaviourandcomparisonofdifferentslabsystemdiagridstructure”,TrendsinCivil EngineeringandChallengesforSustainability,pp.185-198,2021.

[47] Seyedkazemi A., Rofooei F. R., “Comparison of static pushover analysis and IDA-based probabilistic methods for assessingtheseismicperformancefactorsofdiagridstructures”,Vol.28(1),pp.124-137,2021.

[48] DabbagchianI.,MirghaderiS.R.,SayadiS.,“Comparisonofseismicbehaviouroftheeccentricandconventionaldiagrid system”,TheStructuralDesignofTallandSpecialBuildings,Vol.30(3),2021.

[49] LiuC.,FangD.,ZhaoL.,ZhouJ.,“Seismicfragilityestimatesofsteeldiadridstructurewithperformance-basedtestsfor high-risebuildings”,JournalofBuildingEngineering,Vol.52,pp.1044-1059,2022.

[50] ChowdaryM.S.S.K.,KumarY.H.,LingeshwaramN.,“Seismicanalysisoftallconcreteandsteeldiagridstructureusing responsespectrumandtimehistorymethodine-tabs”,IOPConferenceSeries:MaterialsScienceandEngineering,Vol. 1136(1),2021.

[51] KazemiP.GhisiA.,MarianiS.,“Classificationofthestructuralbehavioroftallbuildingswithadiagridstructure:A machinelearning-basedapproach”,Algorithms,Vol.15(10),2022