Grey wolf optimizer trained ANN technique for development of explainable model of commercial ethylen

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

Grey wolf optimizer trained ANN technique for development of explainable model of commercial ethylene oxide reactor and multiobjective optimization to maximize profit

1,2

2 Sucharita Pal1 , Sandip K Lahiri , Chemical Engineering Department, National Institute of Technology Durgapur, Durgapur – 713209 ***

Abstract - The current research focuses on the use of a grey wolf optimizer trained ANN for the building of an industrial reactor model, as well as its optimization for profit maximisation. As a case study, an ethylene oxide (EO) reactor was used. The EO reactor is a multiphase catalytic reactor with a complex nature that makes developing a reliable first principle-based model challenging, while data-driven models lack explanability. As a result, a general methodology has been devised in this study, in which a datadriven technique such as grey wolf optimizer trained ANN was utilised as a modelling tool, and the model was then post-processed to improve the model's explanability. The performance of the model in capturing the system's inherent physics was used to make the decision. Following the creation of an appropriate model, it was subjected to optimization. Maximization of catalyst selectivity and minimization of reactor temperature were examined here, both of which have a significant impact on the plant's profitability. Because the two aims are incompatible, a pareto solution was found by using a multi-objective evolutionary algorithm on the generated model.

Key Words: GreywolfoptimizertrainedANN;Ethyleneoxidereactor;Modelling;Optimization;Geneticalgorithm

1.INTRODUCTION

Duetointenseglobalcompetition,thebusinessenvironmenthaschangeddramaticallysincelastdecade.Chemicalprocess industriesareseeingtheirprofitmarginsdwindleasaresultofincreasedcutthroatcompetitioninavolatilemarket,thanksto globalization.Furthermore,thedevelopingenvironmentalconcernofglobalwarminghaspromptedgovernmentauthoritiesin severalcountriestoestablishrigorousenvironmentalregulations,whichaddtotheexpenseofdoingbusiness.Theonlywayto successfullyminimizethesedifficultiesisthroughtechnologicalinnovationtoimproveprocessandenergyefficiency,yield maximization,andenvironmentalimpactreduction.Chemicalfirmsallaroundtheworldarelookingfornewandimaginative methodstosavecostsandincreaseprofits.Oneofthemostappealingcreativestrategiestoexploreistheuseofartificial intelligence-based techniques to extract value from massive amounts of plant operating data through data mining and knowledgediscovery.

Chemicalreactorsareattractingtheattentionofresearchersandplantmanagerswhoarelookingfornewwaystocreatemore profit.Thereactoristheonlysignificantpieceofequipmentthataddsrealvaluetorawmaterialsbyconvertingtheminto finishedproducts.Reactoroptimizationhasahugepotentialimpactontotalplant profitabilityinthisregard[1].Modeling complicatedsystemsofindustrialchemicalprocessesisessentialasafirststepinoptimizingthecommercialreactor.Complex reactionkineticsandthermodynamicswereinvolvedinindustrialchemicalreactions.Buildingareliablephenomenological model for commercial reactors is a time-consuming and challenging task that necessitates a thorough understanding of industrialheterogeneouscatalyticbehaviorsuchasmassdiffusion,catalystdeactivation,andsoon. Furthermore,several parameterssuchasagitationspeed,catalystinterfacialarea,negativeinfluenceofpoisonspresentinincominggas,diffusional coefficients,andothersaffectreactionrate,yield,andselectivityincommercialplants,themechanismsofwhicharepoorly understood.Asaresult,alackofunderstandingofchemicalreactionkineticsobstructsthereactor'soptimization.Thereactors inmostchemicalplantsremainablackbox,andoperationengineersdonottamperwiththeminaliveplantforsafetyand reliabilityreasons.Thisleadstonon-optimaloperatingofindustrialreactors,whichhasasignificantimpactontheplant's profitability.Asaresult,reactorsareregardedasunchartedareainthechemicalindustry.Inlarge-scaleoperations,however,a slight increase in catalyst selectivity and reaction yield has a significant impact on raw material consumption and plant profitability[1].

Typically,laboratoryscalekineticanalysisisperformedinaveryidealandcontrolledsettingtoderivethekineticequationofa particularcommercialreaction.Becauseofthevastscaleofindustrialreactors,theexistenceofpoisonsandinertininputgases, andthevariedheatandmasstransferenvironment,theuseofsuchamethodforkineticmodellingofindustrialreactorsis debatable.Furthermore,duetothelimitedmarketwindowforchemicalgoods,plantownersarehesitanttodevotesufficient timeandefforttoathoroughexaminationofthesecomplexreactionmechanisms.Asaresult,analternativesimplewayisto

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

useadata-driveneffectivecomputationalstrategytoconstructapproximatedreactormodelsforthesecomplexreactions systemswhichcanbesubsequentlyusedtooptimizethereactorandincreaseprofit.

Becausemostchemicalplantsgatherandstoremassiveamountsofreactorintakeandexithistoricplantoperationaldataevery minute,thetruechallengeisfiguringouthowtousethiswealthofdatatoearnmoremoney.Dataisthenewoil,anddatadrivenmodellingapproacheslikeartificialneuralnetworks(ANN)andsupportvectormachines(SVM)areunquestionablythe newICenginesofourtime.ANNandSVRhavebeenhighlyprominentblackboxmodellingapproachesintherecentdecade, withanumberofapplicationsdevelopedforcommercialreactors.Plantengineers,ontheotherhand,dislikeANNandSVM modelsbecauseoftheirlackofexplainabilityandthemodel'sblackboxnature.ANNmodeldoesnotprovideanyinsightsof underlyingphysicsofchemicalreactors.

BecauseANNmodellinggivesablackboxtypeequationconsistingofacomplexsigmoidalfunctionwithmultipletuningfactors knownasweightsandbiases,themodelsuffersfromexplainabilitylimitations,despiteitsgreatpredictioncapacity.Process engineers typically desire comprehensible equations in differential/ algebraic form that relate output variables to input processparameterssotheycangainmoreinsightandbenefit.Itispreferablethatthegeneratedmodelincludeaclosedform equationthatcandescribetheeffectofkeyprocessparametersontheoutputvariable.SVMhasthesameproblemasANNin thatnoneofthemprovidesclosedformexplainableequationsthatareportableandeasytoimplementinaplantDCSsystem. Forplantengineers,gaininginsightsandobtainingaclosedformexplainablemodelequationiscriticaltotheiracceptanceof usingthemodelintheplant.

DespitetheANNapproach'simpressivepredictioncapabilities,applicationsofthistechnologytochemicalreactionengineering jobs in commercial reactors are conspicuously lacking. In this study, an attempt was made to apply ANN modelling to a commercial chemical ethylene oxide (EO) reactor. One of the key goals of this research is to turn the ANN model into an explainableclosedformequation,whichwillrevealimportantinformationaboutthephenomenologyofthereactor.

Thesecondgoalofthisworkistouserecentlydiscoverednature-inspiredgreywolfoptimizationapproachestotraintheANN model.Learningisanimportantcomponentofeveryneuralnetwork,anditisattractingtheattentionofmanyacademics.The traditional[7]orenhanced[8–10]Back-Propagation(BP)algorithmhasbeenusedtotrainfeedforwardneuralnetworks (FNNs)inmostapplications.TheBPmethodisagradient-basedalgorithmwithsomeflaws,includingdelayedconvergence [11]andapossibilitytogetstuckinlocalminima[12].DuringthelearningprocessofFNNs,thegoalistoidentifythebest combination of connection weights and biases to achieve the least amount of error. FNNs, on the other hand, frequently convergeonpointsthatarethebestanswerlocallybutnotglobally.Inotherwords,ratherthantheglobalminimum,learning methodsleadFNNstolocalminima.Accordingto[11],theBPalgorithm'sconvergenceisstronglydependentontheweights, biases,andparameters'initialvalues.Usinguniqueheuristicoptimizationmethodsorevolutionaryalgorithmstoimprovethe problemsofBP-basedlearningalgorithmsisacommonoptionintheliterature.

SimulatedAnnealing(SA)[13,14],GeneticAlgorithms(GAs)[15],ParticleSwarmOptimization(PSO)algorithms[16–20], MagneticOptimizationAlgorithm(MOA)[21],andDifferentialEvolution(DE)[22]aresomeoftheheuristicoptimization methodsthathavebeenutilizedtotrainFNNs.Accordingto[11],somealgorithms,suchasSAandGA,canlessenthelikelihood oflocalminimatrapping,althoughtheystillhavepoorconvergencerates.

Despitethefactthatnumerousmeta-heuristicshavebeenusedwidelyinANNlearning,noneofthemhasperformedwellinall applications.Furthermore,existingmetaheuristicshaveanumberofdrawbacks[23-27],includingslowconvergencespeed, trappinginlocalminima,longcomputationaltime,tuningmanyparameters,andadifficultencodingscheme.Asaresult,it appearsthatimprovingtheperformanceofpriormeta-heuristicsorproposingnewonesisrequiredtoimprovetheefficiency ofANNlearninginvariousdomains.GWOisarecentinnovativestochasticandmetaheuristicoptimizationapproach,whichis introducedby[18].Inthispaper,theefficienciesofGWOtechniqueareinvestigatedfortrainingFNNs.

The current study opted to model a commercial EO reactor because of its significant financial significance in worldwide petrochemicalmarkets.Becauseitisusedtomakepolyester(whichisusedtomaketextile)andPETbottles,theethyleneglycol industryisregardedthesecondmostsignificantpetrochemicalproductintermsofvolume,profitmargins,andglobalmarket demands.Recently,theglycolsectorhasseenintensecompetitionintheglobalmarket,withplayersvyingforhigherreactor yieldandselectivity,whichhasasignificantimpactonproductioncosts.

Thenextgoalofthisstudyistousethedevelopedmodeltoraisetheprofitoftheethyleneoxideplantwhilereducingits environmentalimpact.Thisisaccomplishedbyusingamodel-based,nature-inspiredmetaheuristicoptimizationmethodto optimize the input process parameters in order to improve selectivity (i.e., reactor performance) while lowering reactor temperature(whichmaximizecatalystlongevity).ThetwomainoperationalobjectivesincommercialEOreactors,namely,

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page405

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

maximizeselectivity(i.e.,maximizeprofit)andminimizereactortemperature(correspondstogreatercatalystlongevity),are mutuallyexclusiveandconflicting,andonecannotachievethehighestselectivitywithoutsacrificingtemperature,andvice versa.Themultiobjectivegeneticalgorithm(GA)isusedtoimprovetheinputspaceoftheEOreactorANNmodelinorderto provideparetooptimalsolutionsthatmeetbothobjectivesinthemostefficientwayfeasible.

2. Case study of ethylene oxide reactor

2.1 Background

Becauseofthelackofunderstandingandcomplexityofmultiphasecatalyticprocessesincommercialethyleneoxidereactors, trustworthyfirstprinciple-basedmodelsarehardtocomeby.Datadrivenmodellingisafeasiblealternativestrategyduetothe vastamountofreactoroperatingparameterdataavailablefromcommercialreactors.Thecurrentprojectaimstomakeuseofa hugeamountofprocessdatatocreateaframeworkforconvertingthedata'sinformationtoknowledgeandsubsequentlyinto profit.

2.2 Reactions:

Themanufactureofethyleneoxide(EO)isthefirststepintheethyleneglycolmanufacturingprocess.Ethyleneoxideisproduced incommercialglycolplantsbyreactingethylenewithoxygen(Equation1)at230–270°Cand20barpressures.Inadditionto ethyleneoxide,anunfavorablesidereaction(Equation2)producescarbondi-oxide,whichisreleasedintotheatmosphereand hasaseverenegativeinfluenceontheenvironment.Catalystselectivityiscomputedusingequation3andmeasurestheextentof thefirstreaction(desired)relativetothesecondreaction(undesired).Selectivitymaximizationisakeyproductiongoalfor increasingprofitswhileminimizingenvironmentaldamage. (1) (3)

2.3 Process flow diagram

(2)

Figure1[17]showsasimplifiedprocessflowdiagramforthesynthesisofEO.TheEOreactorisashellandtubereactorinwhich thecatalystisputinthetubesideaspackedbedandthereactionsdescribedinEquations1and2occurinthispart.Wateris cycledthroughtheshellsidetorecoverheatbecausethereactionsareexothermic.BecausetheconversionofEOfromethylene andoxygenisverylowparpass,theunreactedreactantsarerecycledbackthroughthecyclegascompressortoboostthe conversion.Inindustrial,unreactedethylene,unreactedoxygen,carbondioxide,methane,EO,nitrogen,(usuallycalledcyclegas) are combined withfresh ethylene and oxygen streams. The reactor outputgas was routed through EOabsorbers andCO2 absorbers,asshowninFigure1.TheEOisselectivelyabsorbedbywaterinanEOabsorber,whilsttheCO2isabsorbedbya carbonatesolutioninaCO2 absorber.Plant'soverallprofitabilityisdeterminedbythecatalyst'sselectivity,andplantaimsto decreasesthesecondundesiredreactionwhilemaximizingthefirstfavorablereaction.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

FIGURE 1: ProcessflowdiagramofEOproductionprocess

2.4 Production Objectives:

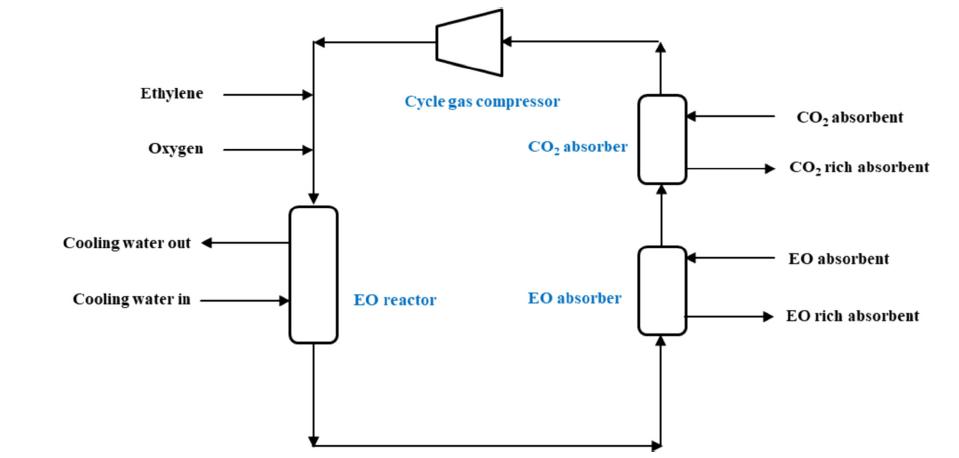
Thecatalystselectivitydeclinesgraduallywiththeageofthecatalystduetocatalystpoisoningandsinteringeffects,andthe catalystselectivitymaintainsabout90%atthestartofoperation(SOR)anddropsto80%attheendofoperation(EOR)(usually after2-4years).Theaveragecatalyticlifeoftoday'scatalystsisbetween24and48months.Thetemperatureofthereactoris graduallyincreasedoverthelifeofthecatalyst[sayfrom225˚C(SOR)to275˚C(EOR)]toenhancethereactionrateandkeepthe plantproductionontargetwhileselectivityisdropping.Theselectivityofthecatalystimpactstheplant'sprofitability,asbetter selectivitymeanslessconsumptionofexpensiveethyleneandoxygentoproducesameamountofEOi.e.,lessproductioncost. Reactortemperature,ontheotherhand,determinescatalystlongevity.Afasterriseinreactortemperaturecausesalossof catalystageandahigherfixedcostofcatalystreplacement,whichnecessitatesaplantdowntime.Optimizingreactoroperating parametersinsuchawaythatselectivitymaximizationandreactortemperatureminimization(i.e.,maximizationofcatalyst longevity)areachievedsimultaneouslywhilemaintainingplantproductiontargetsaretwoprimaryproductionobjectivesin commercialplants.

3. Hybrid FNN- GWO methodology

Thissectionexplainsthebasicbackgroundmaterialsneededforathoroughcomprehensionofthesuggestedmethod.TheMultilayerperceptron(MLP)asaFeed-forwardneuralnetwork(FNN)isfirstpresented,followedbytheGWOmethods,whichare thencomparedtothesuggestedtechniqueforMLPlearninginindustrialreactorsmodelling.Aquickexplanationofthehybrid ANNandGWOtrainingprocessfollowsMLPnetwork.

Becauseofitscapabilitytomapanyfunctiontoanindefinitedegreeofprecision,thefeed-forwardneuralnetwork(FNN)isone ofthemostprevalentANNsusedtosolvereallifeproblemsandattractsalotofacademicattention.Themulti-layerperceptron hasbeenextensivelyusedinfinance,medicine,engineering,geology,physics,andbiology,amongotherfields.Ithasbeenwidely usedinthechemicalindustryfornonlinearprocessmodelling,faultdiagnostics,andprocesscontrol.

MLPhasoneinputlayerthatreceivesexternalinputs,oneormorehiddenlayers,andoneoutputlayerthatdisplaystheoutput, asshowninFigure2.Exceptfortheinputlayer,alllevelsarebuiltupofprocessingnodesandactivationfunctions.Data is suppliedattheinputlayer,andnetworknodesperformcalculationsinsuccessivelayersuntileachoutputnodeobtainsan outputvalue.

3.1 Training of ANN by GWO

Ingeneral,therearethreewaystotrainFNNswithaheuristicalgorithm.First,heuristictechniquesareusedtodiscoverthebest combinationofweightsandbiasesforaFNNwiththeleastamountoferror.Second,heuristicalgorithmsareusedtodetermine thebeststructureforaFNNineachproblem.Thefinalwayistotunetheparametersofagradient-basedlearningsystem,such asthelearningrateandmomentum,usinganevolutionaryalgorithm.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

BeforetrainingFNNs,thestructureisfixedinthefirstscenario.Atrainingalgorithm'sjobistodiscoveragoodvalueforall connectionweightsandbiasesinordertoreducetheoverallerroroftheFNNs.FNNstructuresdifferinthesecondscenario.To discovertheappropriatestructureforagivenproblem,atrainingprocedureisappliedtoanFNN.Manipulatetheconnections betweenneurons,thenumberofhiddenlayers,andthenumberofhiddennodesineachlayeroftheFNNtochangethestructure.

GWOisappliedtoaFNNusingthefirsttechniqueinthispaper;theseprocessesarereferredtoashybridFNN-GWO.Thismeans thattheFNN'sstructureisfixed,andtheGWOalgorithmfindsasetofweightsandbiasesthatyieldstheleastamountoferrorfor theFNN.ThefollowingessentialelementsmustbedefinedinordertodesignFNN-GWO.ToevaluatefitnessinFNN-GWO,first developa fitnessfunctionbased ontheFNN'serror.Second,fortheagentsofFNN-GWO,anencodingapproachshouldbe establishedtoencodetheFNN'sweightsandbiases.Thesecomponentsaredetailedinfurtherdetailbelow.

3.2 Fitness function

Thefollowingistheformulaforthefitnessfunctionusedinthisarticle[10]:

Thenumberofinputnodesisequalton,thenumberofhiddennodesisequaltoh,andthenumberofoutputnodesisequaltom inFigure2,whichhastwolevels(oneinput,onehidden,andoneoutputlayer).Eachhiddennode'soutputiscalculatedas followsattheendofeachlearningepoch: ,j=1,2,…,h (4)

In ,nisthenumberoftheinputnodes,wijistheconnectionweightfromtheithnodeintheinputlayertothe jth nodeinthehiddenlayer,Ɵj isthebias(threshold)ofthejth hiddennode,andxiistheith input. Aftercalculatingoutputsofthehiddennodes,thefinaloutputcanbedefinedasfollows: ,k=1,2,…,m, (5)

wherewkjistheconnectionweightfromthejthhiddennodetothekthoutputnodeandƟkisthebias(threshold)ofthekthoutput node.

Finally,thelearningerrorE(fitnessfunction)iscalculatedasfollows: (6) (7)

whereqisthenumberoftrainingsamples, isthedesiredoutputoftheithinputunitwhenthekthtrainingsampleisused,and istheactualoutputoftheithinputunitwhenthekthtrainingsampleisused.Therefore,thefitnessfunctionoftheithtraining samplecanbedefinedasfollows:

Fitness(Xi)=E(Xi)

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

FIGURE 2:FNNwitha2-3-1structure

3.3 Encoding strategy

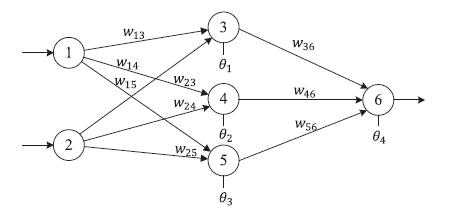
FollowingthespecificationofthefitnessfunctionforFNN-GWO,thenextstepistochooseanencodingstrategyforeachagentin FNN-GWOtoencodetheFNN'sweightsandbiases.Inmatrixencodingstrategy,eachagentisencodedasamatrix.Anexampleof thisencodingstrategyfortheFNNofFigure2isprovidedasfollows: , (8) , , , , (9)

whereW1 isthehiddenlayerweightmatrix,B1 isthehiddenlayerbiasmatrix,W2 istheoutputlayerweightmatrix, isthe transposeofW2,andB2 isthehiddenlayerbiasmatrix.

3.4 Grey Wolf Optimization (GWO): at a glance

Mirjaliliet.Al.[28]introducedGWO,anewstochasticandmetaheuristicoptimizationalgorithm.Twoimportantcharacteristics ofmetaheuristicoptimizationareexplorationandexploitation.Explorationmeanshowquicklyanoptimizationalgorithmable toidentifythepotentialareawheretheglobalminimamayexistfromallfeasiblelargesearcharea.Oncethispotentialareais found,exploitationmeanshowquicklyandaccuratelydetecttheexactpointwheretheglobalminimaexistbydetailsearch.In literature,itisfoundthatGWOalgorithmabletomakeadelicatebalancebetweenexplorationandexploitationbyemulatingthe cooperative hunting behavior of grey wolves in nature. This bionic optimization method promotes the grey wolf pack's hierarchicalsystemandpredationbehavior,inwhichthewolvestakepreybysurrounding,haunting,andattackingitunderthe commandoftheheadgreywolf[31].Inthislarge-scalesearchmethodology,allwolvesformarigidhierarchicalpyramidas depictedinFigure3. butdecisionisbasedonthetopthreegreywolvessitingatthetopofpyramid.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

FIGURE 3:Hierarchyofgreywolf(dominancedecreasesfromtopdown)

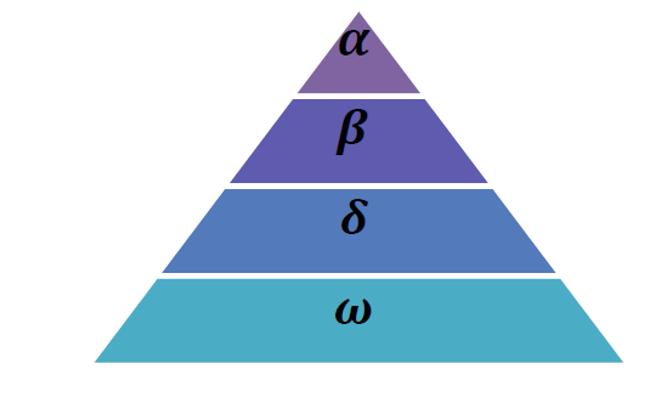
Theaveragegroupsizeis5-12wolves.Thetoplayer(αlayer),whichconsistsofamaleandfemaleleader,istheteam'smost powerfulandcapablememberformakingdecisionsconcerningpredationandotheractivities.Thesecondandthirdlayersinthe hierarchy,βandδlayerrespectively,areresponsibleforassistinginthebehaviorofgrouporganizations.Mostoftheoverall populaceresidesinthebottomofthepyramid,whichisreferredtoasωlayer.Theyareprimarilyinchargeofsatisfyingthe entirepackbybalancingthepopulation'sinternalrelationships,caringfortheyoung,andsustainingthedominancehierarchy [28].

3.5. Mathematical modelling of GWO:

ThemainkeypointoftheGWOmodelisthesocialhierarchy,encircling,hunting,attackingandsearchingprey.

A) Social hierarchy

InthemodelofGWO,αisconsideredasfittestsolution.βandδareconsideredassecondandthirdbestsolution,respectively. Therestofthesolutionsareassumedtobeω.

B) Encircling

Atfirst,thelocationofthepreyisdeterminedandduringthehuntingprocessgreywolvesencircledtheprey.Thefollowing equationsareproposedformathematicallymodelling[28].

(10) (11)

Where isthenumberofcurrentiterations, isthepositionvectorofonegreywolf, isthenextpositionvectorit arrives, isthepositionvectoroftheprey, and arecoefficientvectorswhichareevaluatedasfollows:

(12)

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

(13)

and are random vectors in [0,1], a is decreasing value during the iteration in [0,2], typically (I is the maximumnumberofiterations).

Inthisconcept,greywolvesmovearoundthebestsolutioninhyper-cubeswithinanndimensionalspaceandabletodetectthe positionofthepreyandencircleit.

C) Hunting

Afterencirclingtheprey,greywolveshavetheabilitytohuntthepreywiththeguidanceofalpha.Thebetaanddeltaalsotake partoccasionallyinhuntingprocess.Inthemathematicalstimulationofhuntingbehaviour,thefirstthreebestsolutionsupdate thepositionofothersearchagents(includingtheomegas).Thefollowingequationsareproposedinthisregard. (14) (15) (16)

D) Attacking prey (exploitation)

Greywolvescompletethehuntingphaseandreadytocapturetheprey.Forthepurposeofmathematicallymodelling,thevalue of graduallydecrease.Therefore,thefluctuationrateof isalsodecreasedby whereaisdecrementedfrom2 to0overthecourseofiterations.Whentherandomvaluesof ,thenextpositionofsearchagentcanbeinanyposition betweenitscurrentpositionandthepositionoftheprey.When ,thegreywolveswoulddivergefromthepreytoachieve globalsearchandwhen ,thegreywolveswouldconvergetowardsthepreyandcompleteit.

E) Searching prey (exploration)

GWOalgorithmusesanefficientexplorationmethodologybyallowingitssearchagentstoupdatetheirpositiononthebasisof alpha,beta,deltaandattackstowardstheprey.Thismechanismcreatesagooddiversityintheproblemsearchspace.Grey wolvesarestayawayfromeachotherforglobalsearchofpreyandclosetoeachotherforattackingtheprey.For ,values between 1 and -1 are taken. vector is also favoured the exploration technique and random values are used. After generatingtherandompopulation,alpha,betaanddeltadeterminedthepositionofthebestprey.Forselectionofexploration andexploitation,thevalueof isdecreasedfrom2to0respectively. TheGWOalgorithmterminateswhenthecriterionissatisfied.Thismetaheuristicapproachisappliedinvariousreal-world problemsbecauseofitsefficientandsimpleperformanceabilitybytuningthefewestoperators[28-32].

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal |

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

FIGURE 4: PseudocodeofGreyWolfOptimisation

3.6. Hybrid learning FNN network by GWO

Essentially the trainingalgorithm ofFNN isanoptimization problem where optimized set of weigths and biases are to be determinedwhichminimizestheerror(MSE)beweenactualoutputandpredictedoutput.TheoptimizationcapabilityofGWOis utilisedforFNNlearninginthispart.Toimprovetheaccuracyofthenetwork,ahybridlearningofGWOandFNNnetworks (GWO-FNN) is used. By training the network, the algorithm will concurrently determine the set of weights and their correspondingaccuracy.ThenetworkweightsandbiasesoftheFNNnetworkcanberepresentedasaD-dimensionalvector. Equation17definesthevectorforFNN(4).ThedimensionofeachparticleistreatedasthevectorDasgivenbelow:

D=(Input×Hidden)+(Hidden×Output)+Hiddenbias+Outputbias, (17)

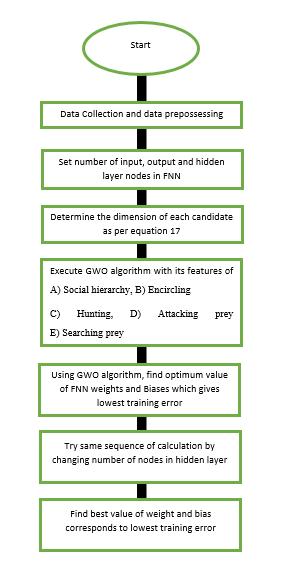
whereInput,HiddenandOutputarereferredthenumberofinput,hiddenandoutputneuronsofFNNnetworkrespectively. The number of biases in the hiddenand outputlayers is alsoknownas Hidden biasand Output bias.Figure 5 depicts the flowchartofGWOandFNNhybridleaning(GWO-FNN).Adatasetiscollected,normalised,andreadtobegintheGWO-FNN. Followingthat,theappropriatenumberofinput,output,andhiddenneuronsarespecifiedtoestablishtheparticledimensionas Equation (7). The population is initialised, and the training error is determined as a fitness function given in equation 17 followingFNNtraining.Everyparticle(wolf)modifiesitsvelocityandpositionbasedontrainingerror.Thenewplacesrepresent theFNNnetwork'snewweights,whicharesupposedtominimisethefitnessfunction.Thefitnessfunctioniscomputedbasedon testseterror.Thesestepswillgoonuntilmeetingstopconditions.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

FIGURE 5: FlowchartofHybridFNN-GWOmethodology

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

4. Mathematical modelling and optimization of EO reaction process

4.1 Selection of input and output variables for modelling

Becauseselectivityandreactortemperaturehavesuchasignificantimpactonplantprofitability,theyarepreservedasoutput variables. Selectivity was chosen because it directly depicts plant production costs and has a significant impact on plant profitability.Reactortemperature,ontheotherhand,impactscatalystlongevityandthusaddsafixedcosttoplantproduction. Fastertemperaturerisesimplyashortercatalystlifeandahighercatalystcost.Asa"wishlist"ofinputvariables,allreactor operationalparametersthatpotentiallyeffectselectivityandreactortemperaturearekept.Forthefirstthreeyears,allEO reactoroperationaldata(dailyaverage)wasgathered.Then,afterconsultingwithaplantexpert,alloftheinputvariablesthat couldaffect the outputvariables were recorded.Following that,a cross-correlationstudy was performed. The correlation coefficients of each of the input variables with each of the output variables, as well as the inter input cross-correlation coefficients,weredeterminedusingthisprocedure.

Theinputvariablesareshortlistedusingthecriteriabelow.

(i) Thereshouldbeastrongcross-correlationcoefficientbetweeninputandoutputvariablesforagiveninputvariable.

(ii) Thevaluesofinterinputvariablecross-correlationcoefficientsshouldbelow.

(iii)Tokeepthemodelassimpleasfeasible,theinputsetofvariableswaskepttoaminimum.

EightinputvariablesarefinallyshortlistedandtabulatedinTable1basedontheaforesaidcriteria.

TABLE 1 InputOutputvariablesformodelbuildingandtheirrange

Variables used in modeling Data Range

Input Variables

Oxygeninletconcentration,mole%(x1) 4.38-7.75

C2H4 inletconcentration,mole%(x2) 17.69-34.97

CO2 inletconcentration,mole%(x3) 0.21-0.45

CGPressure,bar(x4) 21.84–22.64

CGFlow(MT/h)(x5) 687.78–803.39

WorkRate(Kg/hr./m3)(x6) 104.38–202.47

CumulativeEOE(MT/m3)(x7) 275.28–4469.32

Totalchlorideconcentration,PPM (x8) 2.51–5.86

Output Variables

Catalystselectivity,%(Y1) 81.00–89.44

ReactorTemperature,°C,(Y2) 225.83–250.75

4.2. Data collection, Data cleaning and removal of outliers

Datahistoriansoftwareisusedincommercialfacilitiestogatherandstoreeveryoperatingparameterateveryminute.We acquiredEOreactoroperatingdata(dailyaverage)forallparameterslistedinTable1fromacommercialplantthathadbeen operationalfornearlythreeyears.Followingthat,therawdataissubjectedtodatacleaningandoutlierremovaltools.

Becauseindustrydatacontainsnoise,spikes,outliers,anderrorasaresultofmalfunctioningsensors,transmitters,analyzers, controlsystems,anddatahistoriansoftware,datacleansingisoneofthemostimportanttasksinindustrialprocessmodelling.It iscommonlyestablishedthatthequalityofdatautilizedtoconstructadata-drivenmodeldeterminesthemodel'squality.Data qualityisanimportantissuetoconsiderwhenusingdatadrivenmodellingbecausenoisyandfaultydatacanhaveasignificant

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal |

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

impactonmodelperformance.Duetothelargevolumeofprocessdata,thisstudycreatedanautomaticeffectivedatacleaning technique to prevent manual cleaning. From the plant operating dataset, an automated MATLAB-based algorithm was constructedtogenerateamultivariatestatisticalvectorcalledt-squared.Thecorrespondingrowsinthet-squaredvectorwith valuesoverthe95th percentilewasthereforeconsideredoutliersandwereeliminatedfromthedataset.

4.3. Modelling through FNN-GWO algorithm

ThecleanseddatawasusedtocreateanANN-basedmodel.Thedataset,whichincludedeightinputvariablesandtwooutput variables(Table1),wasrandomlypartitionedintoatrainingset(80%ofthetotaldata)andatestset(20%ofthetotaldata).The trainingdatasetwasusedtocomputethemodelbymaximizingthefitnessvalue,whilethetestdatasetwasutilizedtocrossvalidatetheproducedexpression.Thebasicgoalofcross-validationistoimprovethemodel'sgeneralizability.

TheFNN-GWO-basedmodelwascreatedusingcodewritteninMATLAB2019a.Thefitnessfunctionusedinthisworkwasthe mean-squarederror(MSE)betweenactualandpredictedoutputs,andtheprogramwasruninsuchawaythattheMSEvalueof testsetdatawasminimized.Thesoftwarewasrun100timestoconstructthemodelduetothestochasticnatureoftheANN.

4.4. Optimization through Multi objective grey wolf optimization (MOGWO)Algorithm

ThemodelisthenusedtooptimizethereactorprocessparameteronceareliableandaccurateEOreactormodelhasbeenbuilt. ThegoalistoestablishtheidealprocessconditionthatmaximizestheprofitabilityoftheEOplant,andtodoso,thefollowing conflictingcriteriamustbemet:

(i) Theselectivityofthecatalystmustbemaximized.

(ii) Thereactortemperaturemustbekeptaslowaspossible.

In the present work, multi-objective grey wolf optimization (MOGWO) algorithm is used to strike a balance between two conflicting objectives. MOGWO has proven itself to be an excellent multi objective optimization tool and has been used extensivelyindiversefieldofengineeringandmedicine.

Astherearetwoconflictingobjectivesinthisparticularcasestudy,MOGWOisusedtogenerateparetooptimalsolutions.For implementationofMOGWOalgorithm,twoobjectivefunctionsweredevelopedwhichareasfollows(Equation18and19):

F1(x) = 1/(1+Y1(x)) (18)

F2(x) = Y2(x) (19)

Where Y1(x) and Y2(x) arefunctionsofthemodelscorrespondingtocatalystselectivityandreactortemperaturerespectively. Therefore,inMOGWOboth F1(x) and F2(x) havetobeminimizedinordertominimizereactortemperatureandmaximizecatalyst selectivity.

5. Results and discussions

5.1. Performance of FNN-GWO model

ThemaingoalofthisresearchistodevelopaclosedmodelequationforanEOreactorthatisaccurate,simple,portable,andeasy tounderstand.

Thethree-yeardailyaveragedatasetwascleaned,and1220datasetswerequalifiedformodelconstructionafteroutlierswere removed.Atrial-and-errorapproachandaliteraturestudywereusedtodeterminethevaluesofANNparametersrequiredfor modelling.Thenumberofnodesinthehiddenlayerinthecurrentstudyvariessystematicallyfrom5to25,andtheFNNGWO methodisemployedeachtimetodiscoverthebestweightsandbiasthatgeneratethelowestMSEbetweenactualandpredicted output.Theseproceduresgive21[eachmodelforeachnumberofnodes]differentANNmodelwithvaryingaccuracy.

Shortlisting the models: The following criteria were used to pick a viable model from a pool of probable candidates or representativemodelequationswithvarieddegreesofcomplexityandaccuracy:

(i) Simplicity:Themodelshouldhaveaslittlecomplexityasfeasible.Thenumberofnodesinthehiddenlayerwasusedto determinemodelcomplexity.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

(ii) Accuracyofprediction:Thedifferencebetweenexpectedandactualselectivity.

(iii)Themodelequationshouldcapturetheprocess'sunderlyingphysics.Inotherwords,modelequationsshouldcontain physical understandingof the system understudy, notjusta predictiveassociation.Thisisa crucial factor to considerwhilecreatingrealisticreactormodels.Theirplantoperatingknowledge,experienceandobservationsof reactorbehavioraresummarizedinTable2.

TABLE 2 RulestoselectbestmodelfromrealPlantoperationobservations. Sl. no Parameters changed keeping all other parameters constant What happen to selectivity? What happen to temperature? 1 Ifoxygeninletconcentrationincrease Increase Decrease 2 Ifethyleneinletconcentrationincrease Increase Decrease 3 IfCO2 inletconcentrationincrease Decrease Increase 4 IfCGPressureincrease Increase Decrease 5 IfCGflowincrease Increase Decrease 6 IfWorkrateincrease Decrease Increase 7 IfCumEOE/m3 ofcatalystincrease Decrease Increase

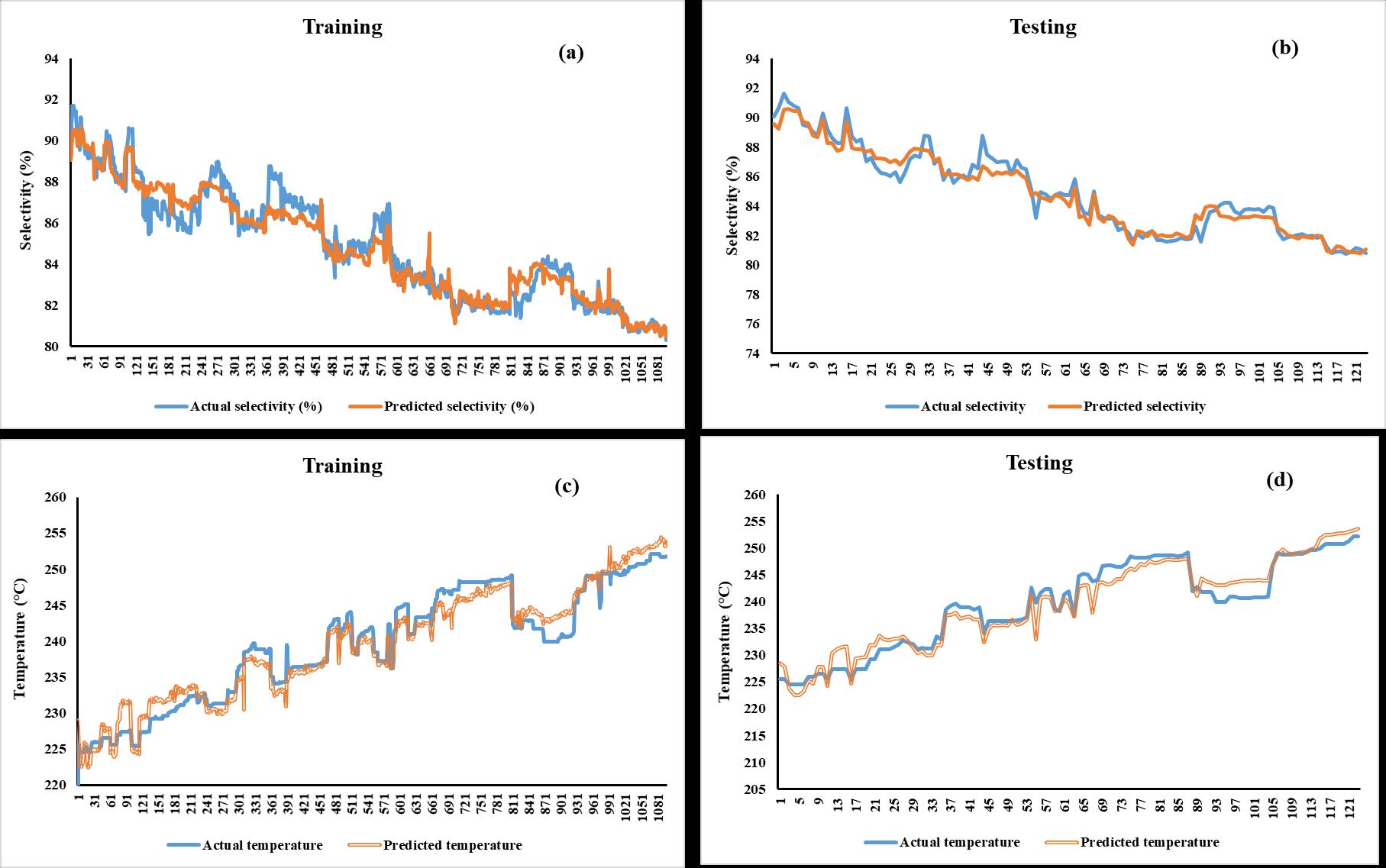
FIGURE 6: Actualvs.predictedplotsof(a)catalystselectivitywithtrainingdata(b)catalystselectivitywithtestingdata(c) reactortemperaturewithtrainingdata(d)reactortemperaturewithtestingdata

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

All21modelsacquiredusingANNaresubjectedtotheaforementionedinspectiontodeterminewhetherthecreatedmodelisin agreementwithplantdata.Alloftheproducedmodelshavebeenthoroughlytested.Assumeaten-testdatasetwasconstructed withallvariablessettotheir50thpercentilevalue,withtheexceptionofoxygeninletconcentration,whichwasalteredin10pointintervalsfromitsminimumtomaximumvalue.Thechartsofoxygeninletconcentrationvs.selectivityandoxygeninlet concentrationvs.temperaturewerecreatedafterthat.Table2observationnumber1wasconfirmedusingthesecharts.Models thatdonotmatchthefindingsinTable2arediscardedbecausetheydonotrepresentthebasicphysicsoftheEOreactoranddo notcorrelatewithplantobservations.Theyareessentiallyrepresentationsofacomplicateddatafittingmodelthatmakesno sense.

Onlyonemodelforcatalystselectivityandonemodelforreactortemperaturewerechosenfromtheshortlistedmodelsbecause theyareexceedinglyprecise,obeytheTable2observations,andcapturetheinternalphysicsofthereactor,suchtwomodelsare consideredtherepresentativemodelequationsforselectivityandtemperature.

ThecorrespondingCoefficientofDetermination(R2)andAveragePercentageError(APE)oftheabovemodelsfortrainingand testdatahavebeenmentionedinTable3.

TABLE 3. PerformanceofANNmodel

Training Testing

Model R2 APE R2 APE

Catalystselectivitymodel 0.99 0.56 0.99 0.56 Reactortemperaturemodel 0.99 0.24 0.99 0.23

WithhighR2andlowAPEforboththecatalystselectivityandreactortemperaturemodels(Table3),itcanbeconcludedthatthe predictedoutputvaluesarecomparabletotheactualoutputvaluesandthatthemodelsdevelopedarereliable,fairlyaccurate, andcapturetheinherentphysicsoftheEOreactor.Themodel'sgeneralizabilityandaccuratelearningonnonlinearinputand outputrelationshipsarefurtherindicatedbythestrongR2 valueonunseentestdataandlowAPE.

Figure6depictsthemodels'predictionperformanceontrainingandtestingdata.Thefactthattherealandforecastcurves almostcoincideimpliesthatthemodelhasstrongpredictionaccuracy.

FromTable3andFigure6itisconcludedthatdevelopedmodelishighlyaccurateandreliableasitalsoperformswellwith unseentestdata.

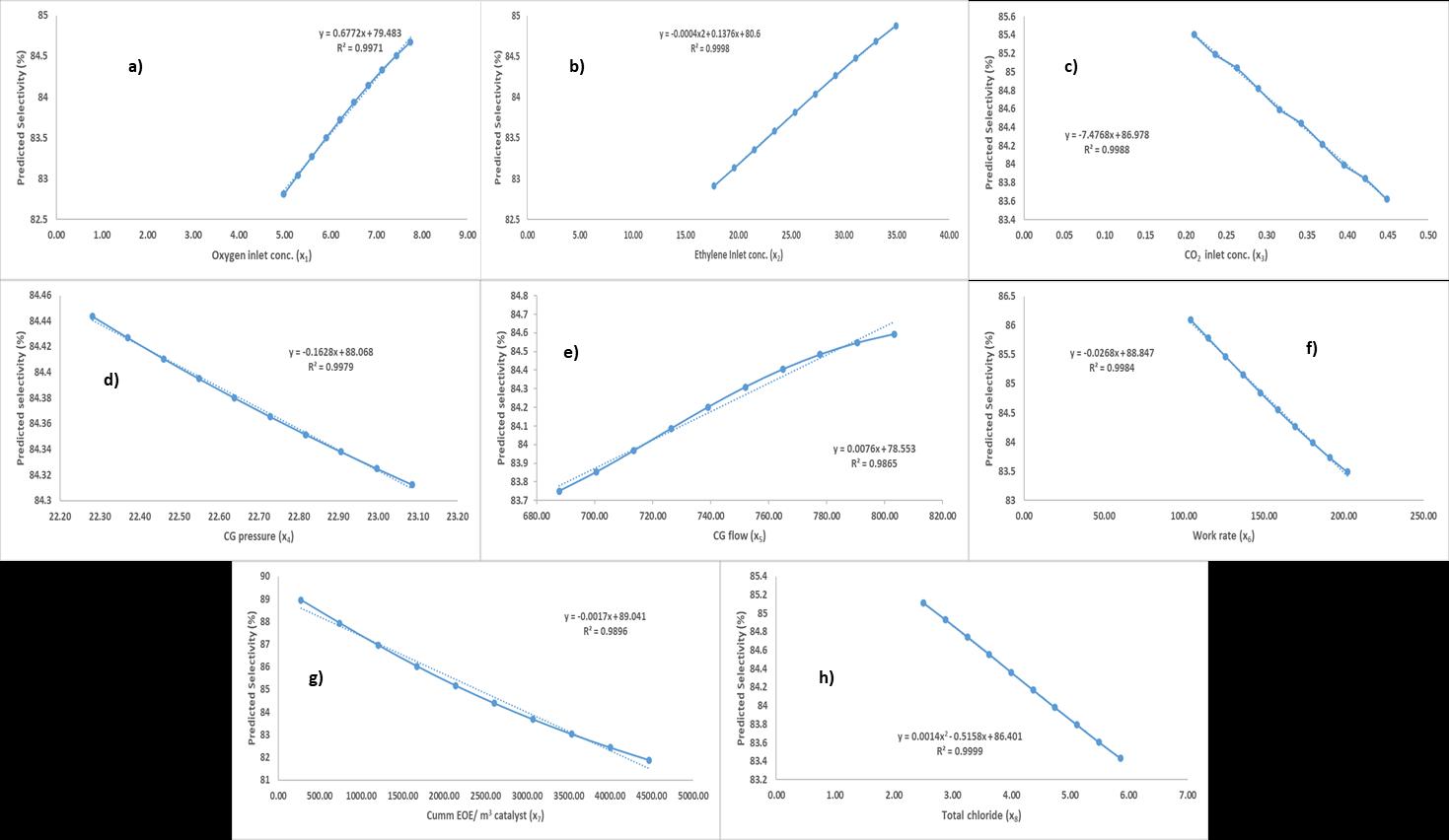
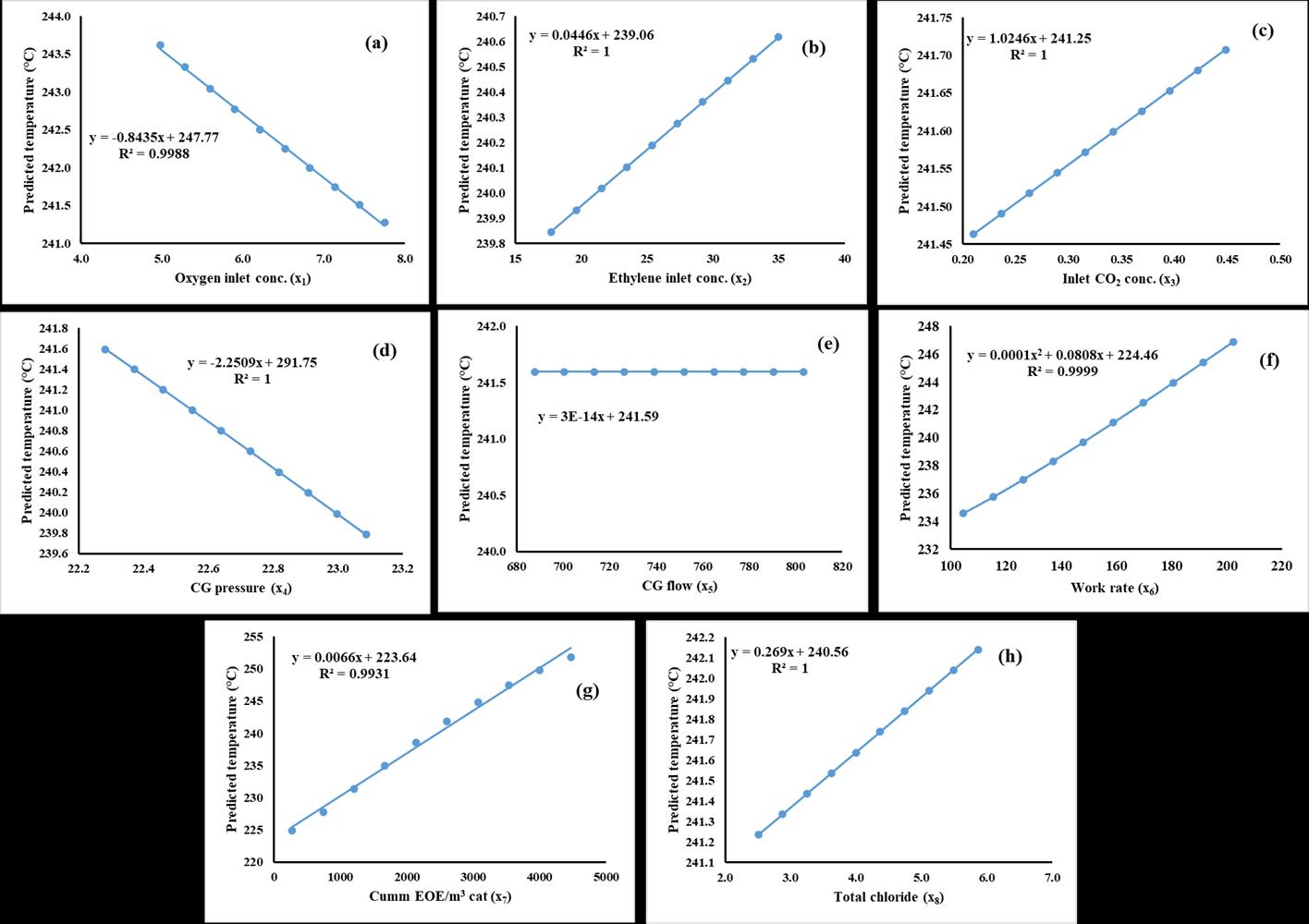
Generation of explainable model equations: ThoughANNgeneratesaclosedformofequationwhichhasveryhighpredictive capability, the developed equation is large and complex and sometimes difficult to directly interpret. In present study, a methodologyisdevelopedtoenhancetheinterpretabilityofthedevelopedequations.Figure7andFigure8summarizethe developedmethodology.Thosefiguresaregeneratedbychangingonevariableatatimefromitsminimumtomaximumvalue (10steps)whilekeepingallother7inputvariablesattheir50-percentilevalue.SelectivityequationsdevelopedbyANNisused topredicttheselectivityvalueineachcaseofthesesimulatedtestdata.Afterplottingwasdone,atrendlinewasdrawnthrough eachdatawhoseequationandR2valueisshowninfigure.BasedonvisualinspectionandR2valuetrendlinecurvewasselected (likestraightline,orpolynomialwithdegree2or3ormore)sothatgeneratedtrendlinealmostmatcheswiththedata.Asseen fromthefigure10,thedevelopedtrendlinesareverydecisiveandmonotonicallyincreasinganddecreasing.Asmentioned earlier,theyallmatchtheplantactualobservationsandobeytheTable2.Inshort,developedmodelscapturesthenonlinear relationshipbetweenselectivityandreactoroperatingparameters.Thesetrendlinescanbeusedbyplantoperatingengineersto gettheinsightshowaparticularinputparameteraffectsthecatalystselectivity.Forexample,fromfigure7,itisquantitively clearthatincreasinginletoxygenandethyleneconcentration,actuallyenhancethecatalystselectivitywhereasincreasingCO2 reducestheselectivity.

Theselectivityincreaseslinearlywithoxygenconcentrationwithpositiveslopeof0.6772,whereastherelationofselectivity withethyleneandCO2arenonlinearandrepresentedbysecondorderpolynomial.Nowthesetrendlineequationsareusedto developthefollowingexplainableequation(Equation20and21).

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

(20) (21)

Where x1, x2, ……x8 aretheactualvalueofthe8inputvariablesand x1, avg, x2, avg, ……x8, avg aretheaverage(50percentile)valueof inputvariables,respectively.

Eachtermintheequation20representsthechangeinselectivityifaparticularparameterdeviatesfromitsaveragevalue.For example,theterm, representsthedeviationoxinletoxygenconcentrationfromitsaveragevalueandwhenit multiplied by co-efficient 0.6772, represents the selectivity gain (or penalty) due to oxygen. In this way, all 8 parameters contributioniscalculatedinequation8anditisaddedwith84.86%(averageselectivity)togettheactualselectivity.

Main advantage of this equation (equation 20 and 21) over ANN model is that this equation is interpretable and easily explainabletoplantengineer.Equationissimpleandcontainstermsorparametricco-efficientwhichthrowlightsrelative importanceofeachparameterontheoverallselectivityiftheydeviatefromthisbasevalue.Also,itindicateswhethertheeffect ofeachparameterislinearornon-linear.

Equation 20 is then used to predict selectivity of three-year actual data and predicted, and actual selectivity is compared. Predictionerroris0.8%andR2is0.97.ThislowvalueofpredictionerrorandhighvalueofR2signifiesthatdevelopedequation (equation20)ishighlyaccurateandreliable.

FIGURE 7: Influenceofeachvariableonselectivity

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

FIGURE 8: Influenceofeachvariableonreactortemperature

5.2. Optimization

5.2.1.

Optimization through MOGWO

Oncethereliablemodelsweresuccessfullydeveloped,themodelsweresubjectedtooptimization.Purposeofoptimizationisto find the optimum value of rector operating parameters to achieve maximum selectivity and minimum temperature simultaneously.Oneofthecriticaltasksforoptimizationofanyprocessisfixingofsearchspaceatwhichtheoptimalprocess conditionsaretobefoundout.Therefore,beforerunningtheoptimizationalowerboundandupperboundoftheprocess variableswerefixedinconsultationwithplantengineers.Asplantconditionsaredynamicinnature,thetotaloneoperational yearwasdividedintothreeperiods(SOR,MORandEOR)andateachrunningperiod,optimizationswereperformed.Thelower bounds(LB)andupperbounds(UB)consideredinthesethreecaseshavebeendepictedinTable4.

Table 4. Lowerboundsandupperboundsforoptimization

x1 x2 x3 x4 x5 x6 x7 x8

Case 1 : SOR

LB 3377 6.37 27.41 1.32 0.15 18.94 5.13 3455.62

UB 3387 9.00 35.12 2.50 0.24 19.95 9.22 4585.31

Case 2: MOR

LB 5377 6.37 27.41 1.52 0.15 18.94 6.13 3455.62

UB 5387 9.00 35.12 2.50 0.24 19.95 9.22 4585.31

Case 3: EOR

LB 8377 6.37 27.41 1.82 0.15 18.94 7.63 3455.62

UB 8387 9.00 35.12 2.50 0.24 19.95 9.22 4585.31

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

WiththehelpofMOGWOcodeinMATLAB,aparetodiagramwasdevelopedforcase2(MOR)(Fig.8).Allthepointsinthepareto curveinFigure.9representstheparetonon-dominatedoptimalsolutionincatalystselectivityandreactortemperaturespace andallParetooptimalsolutionsonthecurveareconsideredequallygood.Asseenfromthecurve,ifsomeonetrytoincrease selectivity,hemustsacrificereactortemperature.Reverseisalsotrue,i.e.,lowertemperaturecanbeachievedatthecostof lowerselectivity.Otherthanthesesolutions,thereisnoprocessconditionwhichcanincreaseselectivitywithoutsacrificing temperatureandviceversa.SomeoftheparetooptimalsolutionshavebeenalsotabulatedinTable5forreference.Fromthe outputofMOGWOtheoptimumvaluesofinputparameterscanbeobtainedwhichwillmaximizetheselectivityandminimizethe temperature.Foursolutionsintable5areplottedasfoursmallblackcirclesonFigure9andrepresentstrade-offbetweentwo conflictingobjectives.Allthefoursolutionsareequallygood,anditisuptotheplantoperationengineerwhichcriteriaamong selectivityortemperaturetheywillgivepriority.Basedonthat,theycanchoosetheoptimuminputparametersfromthePareto optimalsolution.Forexample,ifselectivityhasmoreprioritythanreactortemperatureforaparticularplant,thenoperators shouldchoosesolutionnumber4inTable5whichwillhelptoachieve86.1%selectivitybysacrificingthetemperature(241.53 °C).Ontheotherhand,ifthetemperaturehasmoreprioritythanselectivitythensolutionnumber1inTable4shouldbechosen whichwillgivealowertemperaturebysacrificingselectivity.Iftemperatureandselectivityhaveequalpriority,thensolution number2ofTable5shouldbechosen.

Themainadvantageofsuchastudyisthatitgivestheoperationengineer/DCSpaneloperatorsastrategytorunthereactorin optimumconditioninreal-time.Inarunningplant,sinceoperatorshavenoideaaboutParetooptimalsolution,operatorstryto optimizetheplantheuristicallybasedontheirexperienceandknowledge.Onesuchreal-lifeoperatingpointisplottedand namedas‘A’inFigure.9.Astheoperatingpoint,AisnotontheParetocurve,itisnottheoptimumpointandimprovementscope existsbothinselectivityandtemperature.FromthisplotinFigure.9,itcanbeconcludedthattheoperatorcanimprovetheplant operatingconditionsintwoways:selectivitycanbeimprovedkeepingthetemperaturesameasbefore,orreactortemperature canbedecreasedkeepingthecatalystselectivityasitisasshownbytwoarrowsonFigure9.Theonlyactionoperatormustdois toruntheMOGWOwithproperboundinreal-time,andMOGWOwillprovideasetofoptimumoperatingconditionsthatthe operatorneedstosetintheplant.ThisisthepotentialimprovementareasuggestedbytheParetooptimalsolution.

A

FIGURE 9. Paretodiagramofcatalystselectivityvs.reactortemperature

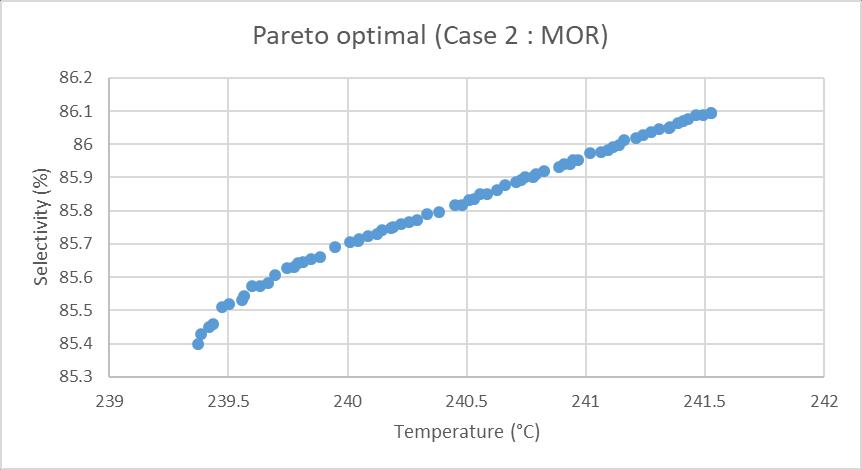
Table 5. Paretooptimalsolution

7.75 18.25 0.31 22.64 782.15 161.09 2572.84 2.59 85.40 239.37

7.75 28.09 0.31 22.54 785.62 161.08 2572.84 2.52 85.71 240.01

7.74 28.18 0.31 22.17 785.93 161.09 2572.84 2.52 85.92 240.82

7.74 28.71 0.31 21.86 785.96 161.07 2572.84 2.53 86.10 241.53

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056 Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072

6. Conclusion

From the existing plant operating data, this study uses Artificial Neural Networking to construct an accurate model of a commercialethyleneoxidereactor.AnANNcreatesaclosedmodelequationthatisportableandmaybeusedinaplantcontrol system.Thetruevalueofthisresearchisthatithasproducedanexplainablemodelequationthatisveryaccurateandprovides insightsintotheprocess.Theproducedmodelequationsarebasedontheunderlyingphysicsoftheprocessandareinlinewith theobservationsandexperiencesoftheplantengineer.Afterthat,thedevelopedmodelequationsareusedtoconstructmultiobjective pareto optimum solutions that optimize selectivity while lowering reactor temperature and thus ensure profit maximization.

REFERENCES

[1] Lahiri,S.K.,2020.ProfitMaximizationTechniquesforOperatingChemicalPlants.JohnWiley&Sons.

[2] Lakshminarayanan,S.,Fujii,H.,Grosman,B.,Dassau,E.,Lewin,D.R.,2000.Newproductdesignviaanalysisofhistorical databases.Comput.Chem.Eng.24,671–676.https://doi.org/10.1016/S0098-1354(00)00406-3

[3] Grosman,B.,Lewin,D.R.,2002.Automatednonlinearmodelpredictivecontrolusinggeneticprogramming.Comput. Chem.Eng.26,631–640.https://doi.org/10.1016/S0098-1354(01)00780-3

[4] Searson,D.,Willis,M.,Montague,G.,2007.Co-evolutionofnon-linearPLSmodelcomponents.J.Chemom.21,592–603. https://doi.org/10.1002/cem.1084

[5] Barati,R.,Neyshabouri,S.A.A.S.,Ahmadi,G.,2014.Developmentofempiricalmodelswithhighaccuracyforestimation of drag coefficient of flow around a smooth sphere: An evolutionary approach. Powder Technol. 257, 11–19. https://doi.org/10.1016/j.powtec.2014.02.045

[6] Floares, A.G. and Luludachi, I., 2014. Inferring transcription networks from data. In Springer Handbook of Bio/Neuroinformatics(pp.311-326).Springer,Berlin,Heidelberg.

[7] Horne,B.G.,1993.Progressinsupervisedneuralnetworks.SignalProcess.Mag.IEEE10,8–39.

[8] Hagan,M.T.,Menhaj,M.B.,1994.TrainingFeedforwardNetworkswiththeMarquardtAlgorithm.IEEETrans.Neural Networks5,989–993.https://doi.org/10.1109/72.329697

[9] Adeli,H.,Hung,S.L.,1994.AnAdaptiveConjugateGradientLearningAlgorithm.Appl.Math.Comput.62,81–102.

[10] Zhang,N.,2009.Anonlinegradientmethodwithmomentumfortwo-layerfeedforwardneuralnetworks. Appl.Math.Comput.212,488–498.https://doi.org/10.1016/j.amc.2009.02.038

[11] Zhang, J.R., Zhang, J., Lok, T.M., Lyu, M.R., 2007. A hybrid particle swarm optimization-back-propagation algorithm for feedforward neural network training. Appl. Math. Comput. 185, 1026–1037. https://doi.org/10.1016/j.amc.2006.07.025

[12] Gori,M.,Tesi,A.,1992.Ontheproblemoflocalminimainbackpropagation.IEEETrans.PatternAnal.Mach. Intell.https://doi.org/10.1109/34.107014

[13] Shaw,D., Kinsner, W., 1996. Chaoticsimulatedannealingin multilayerfeedforward networks.Can.Conf. Electr.Comput.Eng.1,265–269.https://doi.org/10.1109/ccece.1996.548088

[14] Koh, C.S., Hahn, S.Y., 1994. Detection of Magnetic Body using Artificial Neural Network with Modified SimulatedAnnealing.IEEETrans.Magn.30,3644–3647.https://doi.org/10.1109/20.312730

[15] Montana,D.J.,Davis,L.,1989.TrainingFeedforwardNeuralNetworksUsingGeneticAlgorithms.Proc.11thInt. Jt.Conf.Artif.Intell.-Vol.189,762–767.

[16] Kiranyaz, S., Ince, T., Yildirim, A., Gabbouj, M., 2009. Evolutionary artificial neural networks by multidimensional particle swarm optimization. Neural Networks 22, 1448–1462. https://doi.org/10.1016/j.neunet.2009.05.013

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056 Volume: 09 Issue: 11 | Nov 2022 www.irjet.net p-ISSN:2395-0072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page422

[17] Settles,M.,Rylander,B.,2002.Neuralnetworklearningusingparticleswarmoptimizers.Adv.Inf.Sci.Soft Comput.224–226.

[18] Zhang,C.,Li,Y.,Shao,H.,2000.Anewevolvedartificialneuralnetworkanditsapplication.Proc.WorldCongr. Intell.ControlAutom.2,1065–1068.https://doi.org/10.1109/wcica.2000.863401

[19] vandenBergh,F.,Engelbrecht,A.P.,2000.CooperativeLearninginNeuralNetworksusingParticleSwarm Optimizers.SouthAfricanComput.J.26,84–90.

[20] Zhang,C.,Shao,H.,Li,Y.,2000.Particleswarmoptimizationforevolvingartificialneuralnetwork.Proc.IEEE Int.Conf.Syst.ManCybern.4,2487–2490.https://doi.org/10.1109/icsmc.2000.884366

[21] Mirjalili,S.,Sadiq,A.S.,2011.MagneticOptimizationAlgorithmfortrainingMultiLayerPerceptron.2011IEEE 3rdInt.Conf.Commun.Softw.Networks,ICCSN201142–46.https://doi.org/10.1109/ICCSN.2011.6014845

[22] Si,T.,Hazra,S.,Jana,N.D.,2012.ArtificialneuralnetworktrainingusingdifferentialevolutionaryAlgorithmfor classification.Adv.Intell.SoftComput.132AISC,769–778.https://doi.org/10.1007/978-3-642-27443-5_88

[23] Leung,Y.,Gao,Y.,Xu,Z.Ben,1997.Degreeofpopulationdiversity-Aperspectiveonprematureconvergence in genetic algorithms and its Markov chain analysis. IEEE Trans. Neural Networks 8, 1165–1176. https://doi.org/10.1109/72.623217

[24] Hrstka,O.,Kučerová,A.,2004.Improvementsofrealcodedgeneticalgorithmsbasedondifferentialoperators preventingprematureconvergence.Adv.Eng.Softw.35,237–246.https://doi.org/10.1016/S0965-9978(03)00113-3

[25] Liang,J.J.,Qin,A.K.,Suganthan,P.N.,Baskar,S.,2006.Comprehensivelearningparticleswarmoptimizerfor global optimization of multimodal functions. IEEE Trans. Evol. Comput. 10, 281–295. https://doi.org/10.1109/TEVC.2005.857610

[26] Gao,W.feng,Liu,S.yang,Huang,L.ling,2012.Particleswarmoptimizationwithchaoticopposition-based population initialization and stochasticsearchtechnique.Commun.Nonlinear Sci.Numer.Simul.17, 4316–4327. https://doi.org/10.1016/j.cnsns.2012.03.015

[27] Moslemipour,G.,Lee,T.S.,Rilling,D.,2012.Areviewofintelligentapproachesfordesigningdynamicand robust layouts in flexible manufacturing systems. Int. J. Adv. Manuf. Technol. 60, 11–27. https://doi.org/10.1007/s00170-011-3614-x

[28] Mirjalili, S., Mirjalili, S.M., Lewis, A., 2014. Grey Wolf Optimizer. Adv. Eng. Softw. 69, 46–61. https://doi.org/10.1016/j.advengsoft.2013.12.007

[29] Faris,H.,Aljarah,I.,Al-Betar,M.A.,Mirjalili,S.,2018.Greywolfoptimizer:areviewofrecentvariantsand applications.NeuralComput.Appl.30,413–435.https://doi.org/10.1007/s00521-017-3272-5

[30] Saremi, S., Mirjalili, S.Z., Mirjalili, S.M., 2015. Evolutionary population dynamics and grey wolf optimizer. NeuralComput.Appl.26,1257–1263.https://doi.org/10.1007/s00521-014-1806-7

[31] Nadimi-Shahraki,M.H.,Taghian,S.,Mirjalili,S.,2021.Animprovedgreywolfoptimizerforsolvingengineering problems.ExpertSyst.Appl.166,113917.https://doi.org/10.1016/j.eswa.2020.113917

[32] Mirjalili, S., Saremi, S., Mirjalili, S.M., Coelho, L.D.S., 2016. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 47, 106–119. https://doi.org/10.1016/j.eswa.2015.10.039

[33] Pal, S., Chowdhury, S., Hens, A., & Lahiri, S. K. (2022). Artificial intelligence based modelling and multiobjectiveoptimizationofvinylchloridemonomer(VCM)planttostrikeabalancebetweenprofit,energyutilization andenvironmentaldegradation.JournaloftheIndianChemicalSociety,99(1),100287.