Investigating the Physics of Cylindrical Motion

International Research Journal of Engineering and Technology (IRJET)

e-ISSN:2395-0056

Volume: 09 Issue: 10 | Oct 2022 www.irjet.net p-ISSN:2395-0072

Investigating the Physics of Cylindrical Motion

Abstract

ResearchonthephysicsofmotionhascomealongwaysinceNewton’sinfamousobservationofafallingpieceoffruit. Indeed, Newton’s laws of gravitation and motion pervade all areas of mechanics research today. One context in which Newton’s laws of motion have been extensively studied is cylindrical motion. This paper explores the factors that affect cylindricalmotiondownaninclinedplaneviaanextensiveliteraturereview.Inparticular, Iexaminetheangleoftheinclined plane,massandradiusofthecylinder,andsurfacecompositionofthecylinder.Myfindingsareasfollows:Astheangleofthe inclineincreases(uptoacertainangle),thecylindermoveswithagreatervelocitydowntheinclinedplane.Atahighenough angle, the cylinder rolls and slips at the same time, which causes it to have a greater acceleration that when there is only rolling.Themotionof thecylinderremainsunaffected bythemassandradius ofthecylinder. Havinga viscouslayeraround the cylinder plays an important role in lubricating the motion down the inclined plane Studying this topic is of paramount importance due to the huge number of important real-life applications it carries, such as the motion of cartwheels, moving heavyobjectsonaramp,andmore.Thisliteraturereviewprovidesanin-depthanalysisofthedifferentfactorsthataffectthe motion of a cylinder down an inclined plane in the presence and absence of slippage, and thus providing a strong basis for future,morein-depthstudies.

Introduction & Background Information

Researchers have been studying motion in a variety of ways for centuries. In fact, some of the earliest studies on motion date back to as early as 1583, when Galileo Galilei hypothesized that an object would never stop moving on an “infinitely”smoothsurface.Later,around1687,Galileo’shypothesiswasfurtherdeveloped bySirIsaacNewton,whoworked inmanyareasofphysicsandmathematics.Newtonwas amasteratturningtheoriesintopractice;heturnedGalileo’stheory into a Physics practice known as Newton’s first law of motion. Although there is no evidence, it is widely believed that the inspiration behind Newton’s first, second, and third laws of motion emerged when an apple fell on his head while he was sitting in a garden (Isaac Newton, 2022). This caused him to theorize about gravity, which plays a critical role in his laws of motion. Newton’s three laws of motion are defined as follows: (1) An object at rest remains at rest, and an object in motion remainsinmotionatconstantspeedandin astraightlineunlessactedonbyanunbalancedforce;(2)Theaccelerationofan object depends on the mass of the object and the amount of force applied; and (3) Whenever one object exerts a force on anotherobject,thesecondobjectexertsanequalandoppositeforceonthefirstobject.In1686,Newton’sthreelawsofmotion were presented in the “Principia Mathematica Philosophiae Naturalis”. Afterwards, they were used for a wide variety of applications.Forexample,OrvilleandWilburWrightappliedNewton’sLawsofMotiontotheflightoftheiraircraft.

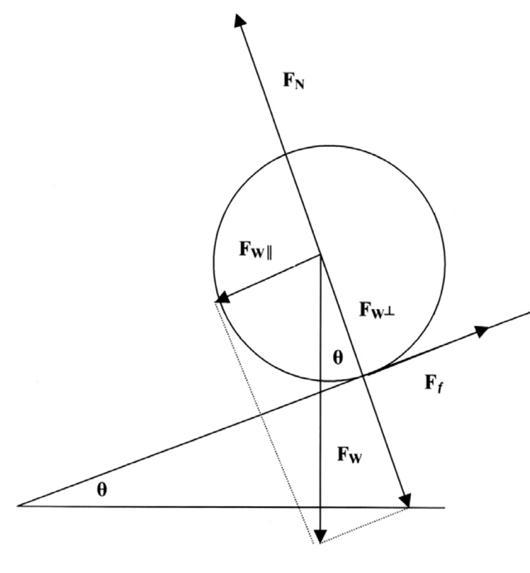
One context where Newton’s Laws of Motion have been extensively studied is in cylindrical motion. A cylinder is definedasa“three-dimensionalsolidthatcontainstwobasescoveredbyacurvedsurface”.Whenthecylinderisplacedonan inclined plane, the component of the force of gravity that is parallel to the surface is unbalanced. The presence of the unbalanced forcewill causetheobjecttoaccelerate downthe inclined plane.Figure 1depictsa cylinderthatisfreelyrolling downaninclinedplane (Chakrabartyetal.)

International Research Journal of Engineering and Technology (IRJET)

e-ISSN:2395-0056

Volume: 09 Issue: 10 | Oct 2022 www.irjet.net p-ISSN:2395-0072

Figure 1 – Cylinder on an Inclined Plane

The source of the rolling motion of the cylinder is its frictional force, as it creates a torque about the center of mass of the cylinder, whichcausesitto roll. Sincethefrictional forceisproportional tothenormal reactionforce,itcanbe deemedthat: ,wherein isthefrictionalforce, isthecoefficientofrollingfriction,and isthenormalreaction force. With reference to this equation, as the value of increases, there will be a decrease in the value of . Thus, the frictionalforcewillgraduallybecomesmaller.Hence,hypothetically,therewillbeapointwhenthefrictionalforceistoo small tomakethecylinderrollasfastastheoreticallyexpected.Thisleadstoslipping;Slippingoccursastheinstantaneousvelocity of the rolling body is not zero at its point of contact with the medium that supports it. In other words, the body rolls and ‘slides’simultaneouslyinthedirectionofitsmotion.

For normal rolling motion (non-slipping conditions), linear velocity and angular velocity are related by the equation In this case, where there is an absence of slippage, the following conclusions about the energy from the cylindricalmotioncanbedrawn,stemmingfromthelawofconservationofenergy.

International Research Journal of Engineering and Technology (IRJET) e-ISSN:2395-0056

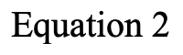
When considering linear kinetic energy: ( ) ( ) ( ) ( )

When considering rotational kinetic energy: ( )

WithreferencetoEquations1and2,itcanbedeemedthatthegravitationalpotentialenergyutilizedinthecylinder’sdescent willalwaysbeintheratioofone-thirdrotationalkineticenergytotwo-thirdslinearkineticenergy,irrespectiveoftheangular orlinearvelocity.Therefore,theratio canbederived.

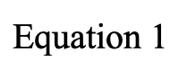
Here, the basic model of a cylinder rolling down an inclined plane has been described which accounts for friction, normal force, and weight. In reality, however, there are many other factors that can impact cylindrical motion in addition to thesethreeeffects.Theprimarygoalofthispaperistoinvestigatesomeoftheotherfactorsaffectingthemotionofacylinder down an inclined plane. After conducting some preliminary research, I hypothesized certain variables that would have an impactonthecylindricalmotiondownaninclinedplane,andthisliteraturereviewfurtherevaluatesthem.Thefactorsthat I shall be examining are the angle of inclination, mass and radius of the cylinder, and surface composition of the cylinder and incline. In the following sections, I elaborate on each of these factors. Such a study aims to help researchers form a strong foundation for futurestudies oncylindrical motion and assists indrawing correlationsbetweenthedifferent variablesthatI haveseparatelyexploredinthispaper.

Volume: 09 Issue: 10 | Oct 2022 www.irjet.net p-ISSN:2395-0072 © 2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page46

International Research Journal of Engineering and Technology (IRJET)

e-ISSN:2395-0056

Volume: 09 Issue: 10 | Oct 2022 www.irjet.net p-ISSN:2395-0072

Angle of the Inclined Plane

The angle of inclination is defined as the angle formed by the x axis and a given line (slope) and is calculated counterclockwise from the positive x axis. When the angle of inclination is low, the cylinder will roll down in the absence of slipping.Whenslippingisabsent,theequation isfulfilled,wherein: v  velocityoftheobject R  radiusofcylinder  angularvelocity

Angular velocity is defined as the time rate at which an object rotates, or revolves, about an axis, or at which the angulardisplacementbetweentwobodieschanges.Intheabsenceofslippage, .Hence,theequationsforthemotionof the cylinder can be derived as  AND when there is a low angle of inclination, wherein ‘a’ is the accelerationofthecylinder,and‘g’istheaccelerationduetogravity.

When the angle of inclination is high enough, the cylinder will slip and roll down at the same time. Slipping occurs whentheobject'scenterofrotationmovesfasterthanvelocityratio,therotationcan't'keepup',andtheobjectslidesoverthe surface. When thecylinder slipsand rollsdown theinclined planeat thesametime, Inthe presence of slipping, the equationsforthemotionofthecylinderareasfollowing:

AND

Withreferencetotheequationsofcylindricalmotioninthepresenceofslippageasshowninthelineabove,if (coefficientof friction)exceedsthecoefficientofslidingfriction,thentheballwillslip.Thus,thereisalimitingangle ,whichisgivenbythe formula .Usingthisequation,thecylinderwillrolldowntheinclinedplanebasedonthe correspondingvalue of Forexample,if is0.2,thentheballwillonlyslipif is orlarger.

Based on an experiment conducted by Cross (2021), it was found that increases as the value of increases, until slipping occurs. If the persisting frictional force is large enough, then the ball can roll in the absence of sliding, which thus causestheaccelerationdowntheinclinetobereducedbyafactorof Inthepresenceofslipping,athighinclineangles, theballwillrollandslipatthesametime,whichcausesittohaveagreateraccelerationdowntheincline,comparedtowhen there is solely rolling. However, the angular acceleration of the cylinder acts differently. The angular acceleration is 0 in the absence of friction. If there is no slipping, then the angular acceleration increases with an increase in the inclination (as increases)untilslippagestartstooccur. Onceslippagecommencestooccur,thentheangularaccelerationbeginstodecrease asthevalueof furtherincreases,andthelinearaccelerationincreases.

Theangularaccelerationofthecylinderisproportionaltoitstorque,which isthetendencyofaforcetoturnortwist andisgivenby .Thus,astheinclination increasesto ,thetorquedecreasesto0.However, canonly reachamaximumvalueof Atasmallvalueof ,thevalueof issmallaswellsinceonlyalittlefrictionisrequiredtomake thecylinderroll.Asthevalueof increases,thevalueof increasesataratefasterthantherateofdecreaseof .Thus,the torque keeps increasinguntil a point where thecylinderstartsto slip. Once reachesa higher value, thevalue of remains constantwhichtherebycausesthetorquetodecreaseasthevalueof isdecreasing.

In the case where the cylinder rolls across a horizontal plane ( incline), there would hypothetically be constant decelerationduetothepresenceofrollingfriction,consideringthatthecoefficientoffrictionremainsconstant. Rollingfriction is the force resisting the motion of a rolling body on a surface. The equations and can be used to deducethedeceleration,where isthefrictionalforcerequiredforrolling, isthemassofthecylinder, istheacceleration, and isthemomentofinertiawithrespecttothediameter.

International Research Journal of Engineering and Technology (IRJET)

e-ISSN:2395-0056

Volume: 09 Issue: 10 | Oct 2022 www.irjet.net p-ISSN:2395-0072

Figure 2 – The effective radius ���� of the ball corresponds to the distance between its mass center and the instantaneous rotation axis (dotted line).

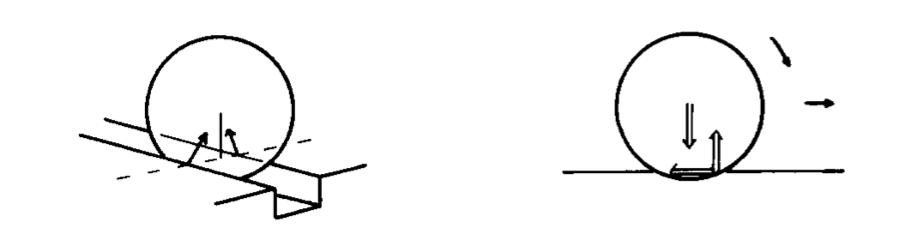
Figure courtesy of A. Doménech (1985)

WithreferencetotheFigure2,since (where istheaccelerationofthecylinder’smasscenter),and ,the

accelerationofthecylinder’smasscentercanbegivenby ( )( ) ,where isthecoefficientofrollingfriction.

Mass and Radius of the Cylinder

The equation of the torque on a cylinder with respect to its point of contact with the inclined plane is given by the equation (where isthetorqueonthecylinder, isthemassofthecylinder, isthe radiusofthecylinder), whichthenleadstoachangeintheangularmomentumwhichisgivenby ,where givestheangularmomentum. (  angularmomentum,  angularvelocity,  momentofinertia) Bycombiningthetwotorqueequationsabove,Iget Therelation (where isthevelocityofthecylinder) canbeusedinthe aboveexpression forangularacceleration toderiveanexpressionforthelinearacceleration,whichis: ,where is acceleration due to gravity. Thus,the acceleration of the rolling object can be written as , .Asa result, the acceleration for the cylinder becomes: . This expression takes neither mass nor radius into account. Thus,itcanbedeemedthatthemassandradiusofthecylinderdoesnothaveanimpactonthemotionofthecylinder

Surface Composition of the Cylinder

Sliding friction, also known as kinetic friction, is the friction between two bodies that are in sliding contact. The coefficientofslidingisdefinedas“avaluethatmeasurestheforceofslidingfrictionforaparticularsurfacetype” (Johnsonand Linde,2022).Thecoefficientofslidinghelpstodeterminewhetheracylinderwouldslideorrolldownaninclinedplane(ifthe coefficient is 0, then the cylinder slides; if the coefficient is 1, then the cylinder rolls). With reference to an experiment conductedbyJ.BicoandJ,Ashmore-Chakrabarty(2009),whenthecylinderisfullyimmersedinaviscousfluid,thefluidforms athinfilmaroundthecylinderinordertochangethecompositionofthecylinder’ssurface Then,whenthecylinderisplaced on an incline plane, the coefficient approximately reaches a value of 0.25, contradicting the higher value of 0.6 when the cylinderisnotdippedintheviscousliquid.Asthevelocityofthecylinderincreased,itwasobservedthattheslidingratiowas close to unity (equal to the original quantity) at lower velocities, and there was transient solid friction between the cylinder andtheincline,whichcouldbeextrapolatedfromthepartiallyerraticmotionofthecylinder.Basedonthisexperiment,itwas found out that thicker lubricating layers resulted in increased sliding. Thus, it can be concluded that viscous liquids (composition) play an important lubricating role in the motion of a cylinder. Overall, the cylinder moved down the incline (coatedwithviscousfluid)withconstantvelocity.Asthecylinderrolled-itslidaswell,whichverifiesthelubricatingrolethat wasplayedbytheviscouslayer.

International Research Journal of Engineering and Technology (IRJET)

e-ISSN:2395-0056

Volume: 09 Issue: 10 | Oct 2022 www.irjet.net p-ISSN:2395-0072

Discussion & Conclusion

Inthisliteraturereview,Iexploredhowdifferentattributesofcylindersandinclinedplanescanimpactthemotionof acylinderdownaninclinedplane.ThefactorsIconsideredincludeangleoftheinclinedplane,massandradiusofthecylinder, andsurfacecompositionofthecylinder.Theaimofthispaperwastoprovideamathematicalexplanationofhowandtowhat extentthesefactorsimpactthemotionofacylinderdownaninclinedplaneaccordingtothelatestliteratureinthisarea.

A limitation of this literature review is that I was unable to physically carry out experiments and get quantitative results for more in-depth analysis and observations, which is what I would have ideally liked to do. Moreover, due to the unavailability of a good online simulation of cylindrical motion down an inclined plane, I was unable to use a simulation to obtain data as well. This topic has a lot of future scope, and I could have explored the impact of other variables on the cylindrical motion, such as density, adhesion, deformation, and the height of the inclined surface. I would have also liked to investigate the distance reached by the cylinders after they have rolled to the bottom of the inclined surface. Moreover, I would have liked to investigate different types of motion of the cylinder, for example – linear motion, rotational motion, translational motion, and non-uniform motion. Furthermore, there is great potential to develop online simulations of cylindricalmotiondownaninclinedplane,sinceitiscurrentlynotavailable.

In conclusion, studying this topic is of paramount importance due to the huge number of important real-life applications it carries along with it such as the motion of cartwheels, moving heavy objects on a ramp, and more. This literature review provides an in-depth analysis of the different factors that affect the motion of a cylinder down an inclined planeinthepresenceandabsenceofslippage,andIhopethatitprovidesastrongbasisforfuture,morein-depthstudies.

References

Ariefka,R.,&Pramudya,Y.(2019,March).Thestudyofhollowcylinderoninclinedplanetodeterminethecylindermomentof inertia.InJournalofPhysics:ConferenceSeries(Vol.1170,No.1,p.012081).IOPPublishing.

Bico, J., Ashmore-Chakrabarty, J., McKinley, G. H., & Stone, H. A. (2009). Rolling stones: The motion of a sphere down an inclinedplanecoatedwithathinliquidfilm.Physicsoffluids,21(8),082103.

Chakrabarty,D.,Dourmashkin,P.,Tomasik,M.,Frebel,A.,&Vuletic,V.(n.d.). Wheelrollingwithoutslippingdowninclinedplane MIT OpenCourseWare, Massachusetts Institute of Technology. Retrieved September 1, 2022, from https://mitocw.ups.edu.ec/courses/physics/8-01sc-classical-mechanics-fall-2016/week-12-rotations-and-translationrolling/37.2-worked-example-wheel-rolling-without-slipping-down-inclined-plane/

Cross,R.(2021).Accelerationofaballdownaninclinedplane.PhysicsEducation,56(3),035017.

Domenech, A., Domenech, T., & Cebrian, J. (1987). Introduction to the study of rolling friction.American Journal of Physics,55(3),231-235.

How was Newton's first law discovered? Socratic.org. (2017, June 21). Retrieved September 1, 2022, from https://socratic.org/questions/how-was-newton-s-first-law-discovered

Isaac Newton: Who He Was, Why Apples Are Falling | National Geographic Society. (2022, June 2). https://education.nationalgeographic.org/resource/isaac-newton-who-he-was-why-apples-are-falling

Janvika Jain, & Kritika Sahu. (2021, October 30). A cylinder rolls up an inclined plane. Sarthaks eConnect | Largest Online Education Community. Retrieved September 1, 2022, from https://www.sarthaks.com/1504238/cylinder-inclined-reachesheight-rolls-without-slipping-throughout-motions-directions

Johnson, R., & Linde, S. (2022, February 28). Sliding Friction: Coefficient, Formula, & Examples. Study.Com. https://study.com/academy/lesson/sliding-friction-definition-formula-examples.html

Kittmer, L. (2019, March 2). List of discoveries of Galileo Galilei. Sciencing. Retrieved September 1, 2022, from https://sciencing.com/list-discoveries-galileo-galilei-8249749.html

International Research Journal of Engineering and Technology (IRJET)

e-ISSN:2395-0056

Volume: 09 Issue: 10 | Oct 2022 www.irjet.net p-ISSN:2395-0072

NASA. (2022, June 30). Newton's laws of motion - Glenn Research Center. NASA. Retrieved September 1, 2022, from https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/newtons-laws-of-motion/

Ocvianti, M. A., Pramudya, Y., & Sukarelawan, M. I. (2021). Numerical Study of Motion of a Cylinder Filled with Water on an InclinedPlaneusingScilab.JurnalFisikadanAplikasinya,17(3),84-88.

Pendrill, A. M. (2020). Balls rolling down a playground slide: What factors influence their motion?.Physics Education,56(1), 015005.

Phommarach,S.,Wattanakasiwich,P.,&Johnston,I.(2012).Videoanalysisofrollingcylinders.PhysicsEducation,47(2),189. https://www.youtube.com/watch?v=esLNxXvwDio

2022, IRJET | Impact Factor value: 7.529 | ISO 9001:2008 Certified Journal | Page50