Design and Analysis of Induction Motor thermal Model for Numerical Protection

Design and Analysis of Induction Motor thermal Model for Numerical Protection

Abstract - As it employs high speed DSP algorithms in microprocessor based relays, present day numerical technology is able to perform much more protectionfunctions in a more reliable and effective manner as compared to its earlier counterparts. The paper discusses one such advancement that became possible in the field of motor protection. IEEE Standard C37.96-2000, Guide for AC Motor Protection [11], recommends the use ofovercurrent relays for overloadandlockedrotor protection.Butthesimpledynamics of an over current relay cannot provide adequate thermal protection for a motor. In the paper the author derives, the thermal model from the thermal limit curves of the motor, which can be used in the relay algorithm to calculate the temperature rise on real time. The relay can be programmed to initiate a trip command, when the heating reaches the threshold. Correlation between the temperature and current has been established, for a 280KW, 6600V motor

Key Words: Numerical Protection, Thremal model, Thermal limit curves, adiabatic process, locked rotor.

1.INTRODUCTION

Thesimpledynamicsofanovercurrentrelaycannotprovide adequatethermalprotectionforamotor.Thethermallimit curvesarethecharacteristicsofthermalmodelsthatenable microprocessorrelaystocontinuouslycalculateandmonitor motor temperature in real time. Employing thermal limit curvesofthermalprotectioninsteadofovercurrentrelaysis one way of optimizing motor protection, because of the varying thermal effects during starting and running of an inductionmotor

II.THERMAL MODEL FUNDAMENTALS

Thefirstorderthermalmodelofaninductionmotorderived consideringmotorasaheatedhomogeneousbodyfollowing non-adiabaticprincipleofthermaldynamicsisgivenbelow. Letthe windingtemperaturerise,θabovetheambient be writtenas,

…………….(1)

where,θisdefinedasthewindingtemperaturerise

θW aboveambienttemperatureθA

The rate of increase of the temperature is given by the equationexpressingthethermalequilibriumconditionas,

PowerSupplied–losses= …….(2)

Cs–Specificheatofthewinding

m–Massofthewinding

Powersupplied= ………………..(3)

And,

Losses= …………………(4)

where R is the thermal resistance in °C/Watt. Now the equationno.2mayberewrittenas, ……………………….(5) (Or)

Itcanbearrangedandwrittenforcurrentas:

……………….(7)

ThemassmmultipliedbythespecificheatCsisknownasC, thethermalcapacityofthesystemwithunitsofjoules/°C.It representstheamountofenergyinjoulesrequiredtoraise the system temperature by one degree centigrade. The product of the thermal resistance R and the thermal capacitance C has units of seconds and represents the thermaltimeconstant.

τ=R.m.Cs=R.C……………..(8)

The solution in the timedomainfor the temperature,asa functionoftimeandcurrentis:

..................(9)

As isthewindingtemperatureabovetheambient,

……………(10)

The final steady state temperature of the winding for a constantcurrentI maybewrittenas:

…………………(11)

Equation no.6 is a first order differential equation and is analogous to a RC parallel circuit supplied by a current source. The power supplied to the motor in the thermal processisequivalenttothecurrentsourcesupplyingtheRC circuit.Thetemperatureinthethermalprocessisequivalent to the voltage across the capacitor in the RC circuit. The equivalencebetweenthetwosystemsisshowninFigure1.

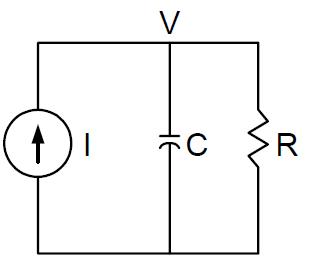
Fig.1EquivalencebetweentheThermalmodelandaParallel RCCircuit

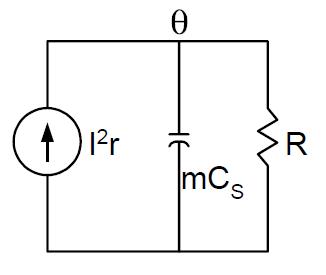
Table.1-ElectricalEquivalenceofthermalmodel

Thermalmodel ParallelRCCircuit

III. EQUIVALENT TIME- CURRENT CURVE

Ifthewindingtemperaturemustnotgobeyondamaximum temperature θmax then the equation with the time as a variableis:

…………….(12)

Solvingfortgivesthetime-currentequation:

…………………..(13)

Let current Imax is the maximum current that can be supplied to the motor without the winding reaching maximum temperature as time goes to infinity. This maximumcurrentwouldhavetosatisfyEquation11asin:

…………..(14) (or)

(a) LoadCurrent

(b)RCEquivalent

…………………(15)

Substitutingθ max -.θA inEquationno.13givestheequation:

…..(16)

InEquationno.16,showsthetotal timetoreachthehot-spot temperatureasafunctionofthecurrent.Equationno.16is also remarkable because it replaces all the temperature constantswiththemaximumcurrentImax

It should be noted that Equation no.16 has no solution unless:

I>Imax………(17)

AnycurrentlessthanImax willraisethemotortemperature to a steady temperature given by equation no.14. This

temperature will be represented by a capacitor voltage in theequivalentcircuitofFigure1.

Thesteadytemperatureofthewindingabovetheambient for any operating current, starting from ambient may be writtenas:

…….(18)

Thetimeresponseequationforthetemperatureriseis:

………(19)

Timeforthetemperatureriseis:

……..(20)

Asperequationno.18,top is:

…….(21)

Finally, the time for a current of magnitude I to heat the motor to its limiting value from an operating current or temperature(motorhotstart)isprovidedby:

….(22)

Finally when normalizing the current with respect to the operatingcurrent,thetriptimeoftherelaywillbe:

……………..(23)

Where:

……….(24)

Servicefactor,SFisthepercentageof overloadingthemotor can handle for short periods when operating normally withinthecorrectvoltagetolerances.

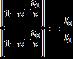
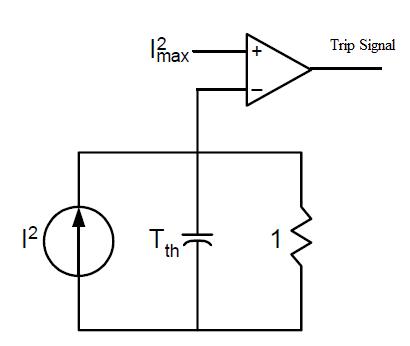
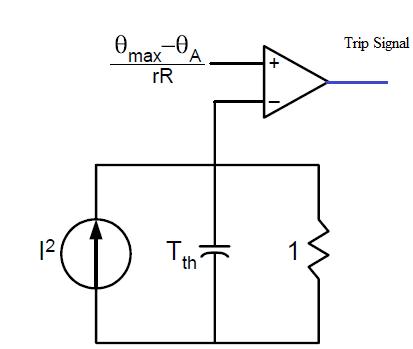
Figure 2 shows the thermal model with temperature and currentasthetrippingthreshold.

(a)Temperatureastrippingthreshold

(b)CurrentasTrippingThreshold

Fig.2ThermalmodelwithTemperatureandCurrentas TrippingThreshold

Letthepairofpoints(I0,T0)and(I1,T1)representthecoordinatesonthetime-currentcurve,correspondingtothe maximumconstanttemperature,then:

……….(25)

Itmayalsobewrittenas:

……..(26)

III. CURVE DESIGN

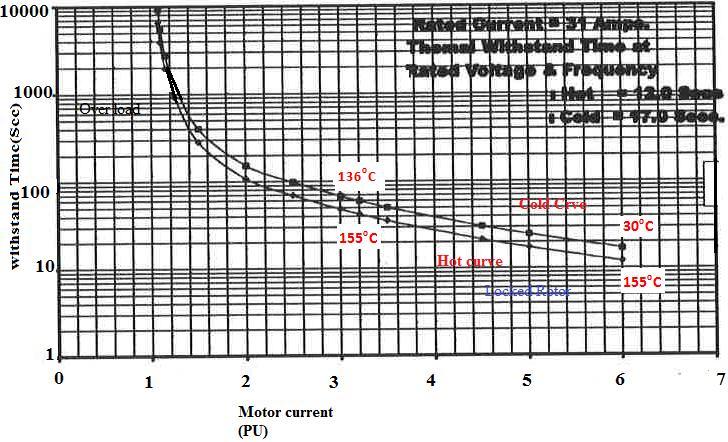
Bydefinition,thethermallimitcurvesgivethetimefor currentexceedingtheservicefactortoraisetheinitialload temperaturetoanoverloadtemperaturethatrequiresthe motor to be disconnected. Each curve is a plot of specific limiting temperature. The relay thermal protection is modeled as per these motor curves. Fig.3 shows thermal curvesfora280KW,6600Vcagerotorinductionmotor.The manufacturerhasspecifiedtheinitialtemperatureforaset of‘hot’and‘cold’overloadandlockedrotorcurves.

As per IEC255, (Equation no.21), the general equation for triptimeforhotandcoldconditionsin termsofperunit valuesare:

…………(27)

Where,

I=Motorcurrentinperunitoffullload.

ISF =Currentattheservicefactor

IH = Current that raised the temperature to a predeterminedfinalvaluewithahotinitialcondition.

IC=Currentthatraisedthetemperaturetoapredetermined finalvaluestartingfromambient.

Thefitisobtainedbysettingthethresholdwhichequalsthe squareoftheservicefactor(SF2).TheequationforSF2 is:

Fig.3ThermalLimitCurves

Ifthecurvesobeyafirstorderthermalprocess,wewillbe abletochooseτ,IH,andIC sothatequationsfitthecurves. Also,IHandICmustbeintheratiooftheinitialtemperatures above ambient. A unique solution obtained with a basic assumptionis:

……………(31)

Forthegivencurves,equation(31)willbecome:

……………(32)

i.e, …………………(33)

IV. CURVE FITTING PROCEDURE

=SF2 ….. (29) (Or) =SF2…..(30)

1.Chooseacurrentandreadthecorrespondingtimepoints fromthehot(155°C)andthecold(100°C)overloadcurvesin Figure3.EnterthecurrentandtimevaluesinEquations29 and30.Forexample,at3per-unitcurrent,thehotand cold timesaretH-CURVE =50secondsand tC-CURVE =65 seconds, respectively.

2.Choose andIH sothatequations29and30aresatisfied. ItisseenthatEquationsaresatisfiedfor, =1000andIH = 0.9Pu.

3. Similarly the other points on the graph can also be checked.

Whentheuniquevaluesforτ , IHandICareused,equations27 and 28 may be used to calculate any curve point with precision.

……………(36)

………….(37)

The above equations are the solutions of a first order differentialequationmentionedinequationno.6.

IV. CORRELATION BETWEEN CURRENT AND TEMPERATURS

According to equations 36 and 37 the squares of the initialcurrentsforhotandcoldconditionsare0.81puand 0.687 pu respectively, which can be taken as the per unit temperaturesinthermalmodel.Whilerelatingtemperature andcurrentsbetweenhotandcoldconditions,theequation obtainedis,

=154.47……….(38)

Where isthemotortemperatureabovetheambientandI is the per unit current. The absolute steady state temperatureϴcanbewrittenas, +30=154.47 +30..(39)

Tabulated values of Current and temperature is given in table2.

Table.2CorrelationofCurrentandTemperature

V. CONCLUSION

Thispaper,introducesthebasicprinciplesandmathematical equationsfoundinthermalprotectionmodelingofinduction motor.Themodelinghasbeendonewithrespecttothe‘hot’ and‘cold’thermallimitcurvesavailableinthedatasheetof themotor.Checkpointshavebeentabulatedaccordingtoa 280KW, 6600V squirrel cage induction motor. The correlation between temperature and current has been established, which proves that all the temperature dependentvariablescanbereplacedbycurrent,makingthe analysismucheasierforanelectricalengineer.

IX. REFERENCES

[1]IEEEStd.620–1996,IEEEGuidefor ThePresentationof ThermalLimit CurvesforSquirrelCageInduction Machines.

[2]S.E.Zocholl, AC Motor Protection,2d Ed.Washington: SchweitzerEngg.LaboratoriesInc.,2003,[ISBN0-97250261-0].

[3]CEI/IEC255-81990-09,ThermalElectricRelays.

[4] S. E. Zocholl, G. Benmouyal, “Using Thermal Limit Curvesto DefineThermalModelsofInductionMotors,” 28th Western Protective Relay Conference,Spokane,WA,October 2001.

[5] S. E. Zocholl, G. Benmouyal, “On the Protection of Thermal Processes,”IEEE Trans. Power Delivery,vol.20,no. 2,pp.1240–1246,Apr.2005.

[6]S.E.Zocholl,E.OSchweitzer,A.Aliaga-Zegarra,Thermal Protection of Induction Motors Enhanced by Interactive ElectricalandThermalModels,” IEEETransactionsonPower Apparatus and Systems, vol.PAS- 103,no.7,July1983

[7] S E. Zocholl, “Optimizing Motor thermal Models” Schweitzer Engineering LaboratoriesInc.,2006.

[8] IEEE Guide for AC Motor Protection, IEEE standard C.37.96 TM -2000(R2006). (Revision of IEEE Std C37.961988)

[9] James H. Dymond, “Stall Time, Acceleration Time, Frequency of Starting: The Myths and The Facts” IEEE

[10]“NetworkProtection&Automation Guide”,Edition May2011,ALSTOM

[11]IEEEStdC37.96-2000, Guide for AC Motor Protection