A Critical Review of Flat Slabs under different parameters

A Critical Review of Flat Slabs under different parameters

1Research Scholar, Dr. CV Raman University, Bilaspur, Chhattisgarh, India

2Professor and Head, Deptt. of Civil Engineering, Dr. CV Raman University, Bilaspur, Chhattisgarh, India

***

Abstract: Flat slabs and other similar slabs are preferred in those structures having larger spans. Due to advancements in civilization emphasis has been put on the construction of newer and more advanced structures like buildings, shopping malls, airports, railway stations, etc. This led to the use of flat slabs for safety, stability, and better design. This works deals with the analysis of critically flat slabs regarding their design, stability, and uses. Cost–benefit analysis gives the economic viability of the use of flat slabs in comparison to other types of slabs. Different design methodologies have been adopted and critically reviewed and inferences are made for the selection of the particular method of designing the flat slab. Using various codes during design are also used for the purpose. The stability of flat slabs under different situations has been critically studied. In civil engineering uses different types of slabs are used in buildings, parking, etc. Using flat slab buildings has numerous benefits over standard RC frame buildings in terms of simpler formwork, space use, architectural flexibility as well as quicker construction times. The analysis demonstrates that flat slab structures are lighter than traditional slab structures. When compared to a standard slab, a flat slab structure is 15 percent less expensive. As per the study's results, flat slab structures outperform traditional slab structures in terms of cost-effectiveness for high-rise structures Flat slab structures result in financial savings, aesthetic views, and greater artistic flexibility for the architect in contrast to typical slab structures. Structures of the flat slab are the highest selection for high-rise structures in comparison to traditional slab structures.

Key Words: Flatslab,Load,Span,Panels,Concrete,ColumnStrip,MiddleStripetc.

Introduction:Theterm"flatslab"isusedtodescribebothareinforcedconcreteslab whichisassistedonlybyconcrete columnsandaslabthatisassisteddirectlywithconcretecolumnswithouttherequirementforbeams.Apanelisapieceof aslabthatisboundedonallfoursidesbyacolumn'scenterline.Panelscanbesplitintomiddleandcolumnstrips.Theflat slab is typically enlarged close to the supporting columns to offer enough shear strength and to decrease the amount of “negativereinforcement”inthesupportzones.(Ghaleb,2015)6 Theword"flatslab"canalsoapplytoasquareslabwitha one- or two-sided support system, known as "drop panels," with the shear stress of the slab being centered on the columns.

Without the need for beams, capitals, or drop panels, flat slabs are “solid concrete” slabs of uniform depth that carry weightstothecolumns(Venugopal et al. 2016)20

It is different from a conventional slab as the latter is supported on beams and columns. Also, a Flat slab has more thicknessincomparisonto a conventional slab. Thistypeofslaboffersa simplerstructure, morearchitectural flexibility, clearspace,quickerconstruction,andsmallerbuildingheight

Structures of flat slab buildings are substantially more flexible during seismic excitations as compared to conventional concrete slabs. The reinforced concrete flat slab is a much-admired idea in structural engineering because it meets architecturaldemandsforbetterillumination,onlyneedsstraightforwardformwork thatcouldberemovedmorequickly (thanotherslabs),andensuresopenvisionwhilemakingthebestuseoftheavailablespace(Sumit

2014)16 .

The constructions designed to support vertical loads may lack the capacity to support lateral loads. The main loads are lateral onesbecausetheyaremorevariableand risemore quicklythanvertical loads,whichare believed to rise linearly with height. The “overturning moment” at the base of the structure is rather substantial and changes in relation to the square of the building's height under seismic loads and identical wind. The top-level experiences significantly greater lateral stresses than the bottom storey, which causes the building to exhibit cantilever behaviour. These lateral stresses cause the frame to tilt. Buildings that weren't built to withstand earthquake loads have failed on numerous occasions in several seismically active regions. The analysis of the impact of lateral loads is crucial in light of all these reactions. The presentpaperrevealsthesuitabilityofflatslabsunderdifferentparameters.

Research Gap: -

Manystudieshavediscoveredthatwhenflat,grid,and traditionalslabswerecompared,forsomestandards,theflatslab hasbeenobservedtobeacceptable,whileatothertimes,thetraditionalslabprovedtobeappropriateforlateralstiffness.

Inthecurrentstudy,anattemptismadetodeterminetheoutcomesforthecompletestructureaswellasmerelytheslab spans. The results are determined, as well as the impact on the columns and foundation when the slab is placed to a seismicload.

Forms of flat slab:

 Flatslabwithoutdropspanelandcolumnhead.

 Flatslabwithdroppanelandcolumnhead.

 Flatslabwithdroppanel.

 Flatslabwithcolumnhead.

Some terminologies related to flat slab

(i) Drop Panels:Thedropfoilisathickerpieceoftheflatslabsurroundingthecolumntopreventshearattheintersection oftheflatslabandcolumn.Itisaslabcomponent.Nootherelementofthestructureissupportedbyit.

(Mehrain and Graf W P M 1992)7 Apillarisonbothsidesofthecolumntopor,moreaccurately,ahigheruprightwitha bitacrossthecolumnatitsmaximumpointonwhichotherstructurescouldrest.Italsoaddstothebaseregion,whichacts asabaseforotherstructures(Apostolska R P et al. 2008)2

(ii) Column Capital:Thepostor“postthrone”thatisgivenatthetopofacolumnisprimarilydesignedtoraisetheslab’s topicssothatpunchingshearsmaybesupported.Thetopofthepostisoftenflaredsothatthecolumn'sgeometryandthe plotgeometrythereareconnected.Thelaw-makinglimitsthesectionofthedesiredpostthatisstructurallyacceptableto thatportionthatfallsinsidethehugepyramidwithnoonof90andmaybeconsideredwithintheconfinesofthepostand postthrone'sshape(Dhangar A L et al 2008)4

Recommendations of the Indian Code for Proportioning Flat Slab:

1)FlatslabThickness:-Thespan-to-effective-depthratiomusttypicallyregulatethethicknessoftheflatslabs.

2)Drops:-Thedrops,ifany,musthavearectangularplanandalengthineverydirectionthatisatleastone-thirdlengthof thepanel.Forexternalpanelshavingdroppedatrightanglestothe“non-continuousedge”andassessedfromthecolumns’ centerline,thewidthofthedropshouldbehalfthatofinteriorpanels.

3) Column heads: - When column heads are offered, the column head’s section that fits totally inside the limits of the columnandthecolumnheadandhasavertexangleof90degreesmustbetakenintoconsiderationfordesign.

Retrofittingcouldbecarriedoutby

 Theinstallationofbeamsonthefloor

 Columnjacketing

 Beamadditionsandcolumnjacketing

Althoughcolumnjacketingisanexcellentcost-effectivemethod,itonlyperformseffectivelyinareaswithlimitedseismic insufficiency.

Design Steps:

1. Calculationofthickness/depthoftheslab

2. Sizeofdrop

3. LoadingCalculation

4. Totaldesignmomentcalculation

5. Calculationofstiffnessandαc

6. Two–wayshearcheck

7. Reinforcementalongshorterandlongerdirection

8. Detailing

ThedesignofaflatslabbasedonthegivendimensioniscarriedoutaccordingtoIS456:2000. SomedesignconstantshavebeenrecommendedbyIS456:2000

“fck =20MPa,Fy =415MPa,Ptmax =0.95”

1.Calculationofthickness/depthofslab: Span 26 x Modification factor Thickness  +cover

2.Sizeofdrop:Itshouldnotbelessthanone-thirdoftheSpan(whetherlongerorshorter)

3.Load:

TotalLoad=Selfweight(deadload)+Finishingload+Liveload+PartitionLoad(ifpresent)

Self-weight=LengthxWidthXtotalThicknessxunitweightofconcrete

Liveload:asperIS456:2000

PartitionLoad:AssumedasperIS456:2000.

Thedesignloadis1.5timesthetotalload

4. Calculation of Moment: The absolute moment (Sum of negative and positive bending moment) (M0) in every direction canbecomputedas:

Windicatesdesignloadforacertainareal2ln

ln –aclearspanbetweenfacesofcolumns,capitals,andnolessthan0.65l1.

l1 –spanlengthindirectionofM0

l2 –spantransverselengthtol1

ThedesignmomentM0mustbespreadinaninteriorspaninthefollowingways:

PositiveandNegativedesignmoments:0.35and0.65

Thenegativedesignmomentoftheexteriorcanbecalculatedas:

Where αc indicates the ratio of the flexural stiffness of the slab's “exterior columns” to the slab at a joint taken inside directionmomentsarebeingcalculatedandisdenotedby

Checkforshear:

Nominalshearstressτv = 0

HereVindicatesashearforceresultingfromdesignload,

b0 denotesthecriticalsection’speripheryand

dsignifieseffectivedepth.

Reinforcement:

Ast –anareaofsteel,

d–effectivedepth

fck –Characteristiccompressivestrengthofconcrete

fy –Characteristicstrengthofsteel

b–Widthofcolumnstrip

Theabovecalculationsaresummarisedanddetailingsaretabulated.

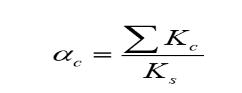
Inthesummary,thegradeofconcrete,steel,thethicknessoftheslab,moment,thequantityofconcrete,steel(%),areaof reinforcement,etc.ismentioned.

Behavior and Performance of Flat Slabs under different conditions:

(a)Load–Multi–StoreyBuildingunderSeismicconditions

(b)Span

(c)Cost

Load: Thefollowingconclusionscouldbetakenfromtheinvestigationsconductedthusfarbyvariousresearchers.

1)Thelackoflateralstiffnessinaflatslabbuildingresultsinaworseseismicresponsethaninaconventionalbuilding.

2) The placement of shear walls within a building has an impact on the “seismic response” of that structure. Since shear wallsoffergreaterlateral“loadresistance”,itiscrucialtounderstandhowflatslabbuildingswithshearwallsbehaveand wheretheyshouldbeplacedinthebuilding

From various studies and research, it has been concluded that storey displacement, as well as bending moment, are greaterforastructurewithaflatslabthanforastandardtwo-wayslab.

We need to know the different loads that are applied to the column to calculate the total load on the column, beam, and slab.TheColumn,Slab,andBeamconfigurationsaretypicallyfoundinframe-stylestructures.

The load is transmitted via the frame structure from “slab” to “beam” to “column” till it finally reaches the building's foundation.Thefollowingelements'loadsmustbedeterminedforthebuilding'sloadcalculation:

Load on Column, Beam & Slab

 Wallsloadperrunningmeter

 NumberoffloorsxColumnSelfWeight

 Self-WeightBeamsperrunningmeter

 Slab’stotalload(Liveload+Deadload+Self–weight)

In addition to the aforementioned loads, the columns are also exposed to “bending moments” , which must be taken into accountinthefinaldesign.

ThevolumeofConcrete=lengthxwidthxthickness

WeightofConcrete=Volumexdensity

SteelWeight(1%)inConcrete

TotalColumnWeight=Weightofconcrete+steel

Thecolumns’self-weightisestimatedtobebetween10and15kN/floorwhenperformingcalculationsforcolumndesign.

2. Beam Load Calculation

Wesupposethateverybeam’smeterhasmeasurementsof(x and y mm)excluding“slabthickness”

Supposebeameach(1m)meterhasameasurementof x and y mmexcludingtheslab.

ConcreteVolume= x x y x1= xy m³

WeightofConcrete= xy xρc (ρc isthedensityofconcrete)

SteelWeight(2percent)inConcrete

TotalWeightofColumn=Weightofsteel+concrete

Asaresult,theself-weightperrunningmeterwillbeapproximately3.5kN.

3. Wall Load Calculation

Weareawarethatbricksrangeindensityfrom1500-2000kg/cubicmeter

Forabrickwallthatissixinchesthickandthreemetershighwithaone-meterlength, Therunning/loadmeterisassumedtobeequivalentto0.150x1x3x2000=900kg,or9kN/meter.

The weight/cubic meter ranges from 550-700kg for aerated concrete as well as autoclaved concrete blocks, such as SiporexorAerocon

4. Slab Load Calculation

Eachsquare meterof theslab’s self–weight should be determined by its length x width x density of concrete Now, if the finishingloadissetat1kNpermeterandtheoverlaidliveloadissetat2kNpermeter

5. Safety Factor

AsPerIS456:2000,thefactorofsafetyis1.5.

Oneofthecrucialcomponentsofeveryconstructionstructureisacolumn.Thebuilding'scolumnsizeisdeterminedbythe weightthatthesuperstructurewillimposeoneachcolumn.

Thecolumnsizeisraisedforbuildingsunderextremeweightsituations.Whendevelopinganyarchitecturalconstruction, thesizeofthecolumnsisacrucialconsideration.

Variationsincolumnsizesareemployedinbuildingdesign,

9"x9";9"x12";12"x12";15"x18";18"x18";and20"x24"

Moresizescouldbeemployedfollowingthestructuralload.

Weneededthefollowinginformationtocalculatethecolumnsize:

(a) ConcreteGrade (b)SteelGradeand(c)FactoredLoadonColumn

(Note:Thecolumn'sminimumsizemustnotbebelow9′′x9′′(230x230mm)

Todeterminethecolumn’ssizeforthebuilding,performthefollowingcolumndesigncalculations

“Pu=0.4fck Ac+0.67fy Asc (ClauseNumber:39.3PageNumber:71IS456:2000)

fck =Characteristicscompressivestrengthofconcrete

Ac =AreaofConcrete

fy =CharacteristicsTensilestrengthofconcrete

Asc =AreaofSteelReinforcement

Pu=AxialLoadonColumn

Ac =Ag –Asc

Asc =0.01Ag

Ac =0.99Ag

HereAg =Column’sGrossArea

Consider1percentofSteelinColumn,

Ac =Ag– Asc ”

Howdoyoudetermineabeam'sslabload?

The slab typically measures 125 mm thick. As a result, the slab’s thickness and the concrete’s per-square-meter load, which is anticipated to be roughly 3 kN, would be the formula for the self-weight of the slab’s every square meter The overallslabloadwillbeintherangeof6-7kN/squaremeterwhenthefinishingloadandsuperimposedliveloadaretaken intoaccount.

Load Calculation of Building (As per IS 456:2000)

Thedead,living,wind,aswellassnowloads,areaddedtogethertoformthebuildingloadwhenabuildingislocatedina snowfallarea.Long-lastingstaticforcesarereferredtoasdeadloads.Theycanbecompressedorinstrain.Themajorityof live loads are varying or shifting loads. These loads might be very dynamic and may consider parameters such as fluid sloshdynamics,vibration,momentum,impact,andsoon.

Dead Loads

Deadloadsmustbecomputedusingunitweightsthataredeterminedwhiletakingthematerialsrequiredforconstruction into account. As an alternative, the dead loads might be examined using the material unit weights from IS 875. (Part 1). The plain concrete’s unit weights and reinforced concrete built with crushed natural stone aggregate or sand and gravel maybeusedasestimatesuntilmoreprecisecalculationsarenecessary.

24and25kN/m3 respectively.

Imposed, Wind & Snow Loads:

TheseloadsmustbefollowingIS87S(Part2),IS87S(Part3),andIS875(Part4)respectively.

Earthquake Forces

TheIS1893standardmustbefollowedincalculatingtheearthquakeforces.

Span: Theslab'sthicknessvariedbetween70,80,90,and100mm.Asthicknessincreased,deflectionfor acorner,aswell as penultimate column failure, decreased. Additionally, it has been shown that for the same weight, the deflection in the cornercolumnfailurescenariowaslowerthanthatinthepenultimatecolumnfailurecondition.

Numerousinvestigationsrevealedthatthedeflectionforacorneraswellaspenultimatecolumnfailurecasesincreasedas slablengthincreased.Additionally,ithasbeennotedthatforthesameweight,thedeflectioninthe“cornercolumnfailure” scenarioislowerthanthatinthe“penultimatecolumnfailure”situation(K, Senthil et al 2018)11

Cost: A function that should be reduced is the materials cost (steel and concrete reinforcement) and the formwork. The slab'soverallcost couldbepresentedasfollows:

“C = Cc x (Qc) + CS x (WS) + Cf x (Af)”

Here,

Cc denotestheconcretecost/unitvolume

Qc indicatestheconcretevolume

CS signifiesthesteelcost/unitofmass

WS denotesthesteel’sweight

Cf representstheformworkcost/unitarea

Af signifiestheform’ssurfacearea

Cindicatesthetotalcostfunction

Thefollowingcostfunctionmaybeusedtodemonstratetheimpactoftheunitcostsofthesteelandconcrete:

Itisconcludedfromtherelationthattherisingoftheratio S

C C leadstoreducingtheentireslabcost,withthereductionin thematerialcostratiohavinglittleimpactontheslab’seffectivedepth.

The cost function may be constructed in the following manner to analyze the impact of formwork cost on the ideal solution:

C=CC xQC +CS xWS

theoptimumratiooftheslab'stotalcost,includingformworkcosts,totheslab'stotalcost,excludingformworkcosts.

Conclusions:

Buildingswithflatslabshaveseveral benefitsover thosewithslab-beam-columns,includinglowerfloorheights,quicker construction times, architectural functionality, and cost-effectiveness. But while beams are not needed in flat slab buildings because columns support the slab directly, shear walls are necessary to stiffen the structure against lateral stresses. Among the most often utilized lateral “load-resisting” systems in “high-rise buildings” is the shear wall system. Thesewallsareextremelystrongandrigidintheplane.Todeterminewhatchangeswilltakeplaceiftheheightofbothflat slab buildings and typical RC Frame buildings increases, it is required to examine the buildings’ seismic behavior for a rangeofheights.

• Swayincreasesasthenumberoflevelsrises

• Thehighestswayoccursattheterracelevelforbothtypesofbuildings.

• WhencomparedtoatraditionalR.C.C.structure,storeydrift(alsoknownasSway)issubstantiallymorecommon inflatslabbuildings.Thisleadstothedevelopmentofmoremoments.Therefore,theextramomentbroughtonby driftshouldbeconsideredwhiledesigningthecolumnsofsuchbuildings.

• Comparedtoflatslabbuildings,typicalR.C.framedbuildingshaveahigherbaseshear.

• Base shear in a flat slab rises steadily for the first three stories, after which it rises relatively slowly. And in a traditionalR.C.frame,itrisesto6levelsbeforegraduallyfalling.

Bending moment and shear force are comparably greater in traditional slab buildings, but the axial force on the column causedbyallloadcombinationsisalmostthesameinbuildings.

Theflatslabhasagreatershearforceaswellasbendingmomentwhenevaluatedtothegridslaband2-wayslab.

Therefore,flatslabconstructionsimprovefromanaestheticpointofviewandprovidethearchitectwithagreatdegreeof formwork flexibility, air pipes, open space for water, ease of casting concrete, ease of placing flexural reinforcement, etc. The lowering of the building height of multi-storey constructions by preserving one storey height etc. between the slab andapotentialfurredceiling.

ThisresultsintheFlatslabbeingmorecost-effectiveascomparedto traditional andGridslabs.Thesestructuresarethe greatestchoiceforhigh-risebuildingscomparedtoGridSlabandtraditionalslabstructures.

References:

1. A.A. Sathawane, Prof. R.S. Deotale [2020] Analysis and Design of Flat Slab and Grid Slab and Their Cost Comparison IJERAVol.1Issue3Pp.837-848.

2. Apostolska R P, Necevska-Cvetanovska G S, Cvetanovska J P and Mircic N (2008) “Seismic performance of flat-slab buildingstructuralsystems”The14thWorldConferenceonEarthquakeEngineeringOctoberpp12–7

3. Apostolska R P, G. S. Necevska – Cvetanovska, and N. Mircic, (2015) “Seismic Performance of Flat Slab Building StructuralSystems”,the14thworldConferenceonEarthquakeEngineering,October12-17,Beijing,China.

2395-0072

4. Dhangar A L and Walke S B (2015) A comparative study of seismic response of flat slab structure and conventional structureInt.J.latesttrendsEng.Technol.

5.Dr.MRameGowda,TechiTata(2016)“STUDYOFSEISMICBEHAVIOUROFBUILDINGSWITHFLATSLAB”International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395 -0056 Volume: 03 Issue: 09 | Sep-2016 www.irjet.netp-ISSN:2395-0072

6. Optimum Design of Reinforced Concrete Flat Slabs” Engineering and Technology Journal, 2015, Volume 33, Issue 9, Pages2049-2065

7. Graf, W.P. et al (1992) “ Analysis and testing of a flat slab concrete building” Earthquake Engineering, Tenth World Conference@Balkema,Rotterdam,USAISBN905410605

8.IS1893(PartI)-2002:IndianStandardCodeofPracticeforCriteriaforEarthquakeResistanceDesignofStructures,Fifth Revision,NewDelhi,June2002.

9.IS456-2000:IndianStandardCodeofPracticeforPlainandReinforcedConcrete.FourthRevision,NewDelhi,July2000.

10.IS875(PartIII)-1987:IndianStandardCodeofPracticeforDesignLoadsforBuildingandStructures,SecondRevision, NewDelhi,February1989.

11. K. Senthil et al (2018) “Study on Influence of Thickness and Span Length of Flat Slab for Progressive Collapse” Proceedings of National Conference: Advanced Structures, Materials and Methodology in Civil Engineering (ASMMCE –2018),03-04thNovember2018

12.MawanRasheed,Dr.RamakrishnaHegde,BhavaniShankar(2019)“COMPARATIVESTUDYONCONVENTIONALSLAB AND FLAT SLABS RCC STRUCTURE USING PUSHOVER ANALYSIS” International Research Journal of Engineering and Technology(IRJET)e-ISSN:2395-0056Volume:06Issue:12|Dec2019www.irjet.netp-ISSN:2395-0072

13.MeeraPradeep,Prof.SabeenaMV(2016)SeismicBehaviorofFlatSlabBuildingStrengthenedwithPerimeterBeams, ShearWallsandBeamSlabinAlternateStorey’sInternationalJournalofInnovativeResearchinScience,Engineering,and Technology.

14. Mohana H.S, Kavan M.R (2015) “Comparative Study of Flat Slab and Conventional Slab Structure Using ETABS for DifferentEarthquakeZonesofIndia”

15.NavyashreeK,Sahana(2014),“Useofflatslabsinamulti-storycommercialbuildingsituatedinthehighseismiczone” volume:03issue:08|aug-2014www.ijret.org

16. Pahwa S, Tiwari V and Prajapati M 2014 Comparative Study of Flat Slab with Old Traditional Two Way Slab InternationalJ.LatestTrendsEng.Technol. 4252–60

17 Pradip S. Lande, Aniket B. Raut, (2015) “Seismic Behavior of Flat Slab System”, Journals of Civil Engineering and EnvironmentalTechnology,Vol.2,Issue10,April-June2015,ISSN:2349-879X,pp.7-10.

18.SanjayPN,MaheshPrabhuKandUmeshSS(2014)BehaviourofflatslabRCCstructure underearthquakeloading Int. J. Eng. Res. Technol. 31386–95

19. Shital Borkar, Kuldeep Dabhekar, Isha Khedikar, Nalini Vaidya (2021) Review on “Comparative study of flat slab structure and conventional slab structure” International Conference on Advances in Civil Engineering (ICACE 2021) IOP Conf.Series:MaterialsScienceandEngineering1197(2021)012072IOPPublishing

20.Venugopaletal.(2018)”ParametricStudyofConventionalSlaband FlatSlabinaMultiStoreyRCBuilding”(IRJET)eISSN:2395-0056,Volume:02Issue:03

21.Varghese,P.C.AdvanceConcreteDesignVolume2,Pertinence-HallofIndiaPrivateLimitedNewDelhi.Pp-158

170