Design Optimization of Filters for Energy Conservation

Design Optimization of Filters for Energy Conservation

Abstract - Every hydraulic system needs a filter since the majority of hydraulic system failures are caused by pollution, dirt, and unclean water. Filters must maintain pump efficiency and flow rate in addition to filtering water Consequently, when headloss is decreased, this is possible. Head loss is essentially the loss from water obstruction caused by filter mesh, filter parts etc. Energy use and head loss are directly correlated. Consequently, the goal of this study is to determine the ideal location and suitable filter for the maximum energy conservation and minimal head loss. Real filters are tested in a virtual environment using CFD and simulation. saving money, energy, and other resources. This also prevents failure of filters in real world In this research with help of cfd simulation using of filters with minimum energy consumption is aimed In order to save energy and increase the effectiveness of hydraulic systems, it is essential to do research on the design optimisation of filters using computational fluid dynamics (CFD). This work attempts to reduce energy losses and pressure drops in the filter by optimising the design of a filter for hydraulic systems using CFD simulations. The shape, size, and flow channel of the filter are changed during the optimisation process, and the ensuing flow behaviour and pressure drop are examined. The identification of areas of flow separation, turbulence, and pressure losses within the filter is made possible by the CFD simulations.DesignchangesaredonebasedontheCFDdata to lower the pressure drop and improve the filter's efficiency.

Key Words: CFD, Energy Conservation, Head Loss, Convergence, Divergence

1.INTRODUCTION

The design and upkeep of hydraulic systems depend heavily on filtration. To achieve dependable system operation, it is vital to regulate the degree of purity of hydraulicfluid.Withoutadequatefiltration,pollutantslike moisture, dirt, and debris can harm hydraulic parts and lead to system failure. Therefore, for optimum performance and to prevent downtime, correct filter design,installation,andmaintenancearecrucial.

Itisessentialtoobtainaccuratedataonfilterperformance in real-world settings in order to build an effective filter

for a hydraulic system. Using this knowledge, engineers mayselectthebestfilterforthejobathandandmaximize its designspecifications,includingthe filtermedium,pore size, and geometry. By doing this, they can reduce pressure drop and service intervals while achieving the appropriate level of filtering efficiency and dirt removal capacity.

However, filtration effectiveness and dirt-removal capability are not the only factors to consider when choosingafilterforagivenapplication.Itisalsonecessary to consider additional elements like pressure drop and flow rate handling capabilities. For instance, if the filter's flow rate is too low, pressure may build up and the system's effectiveness may suffer. However, if the flow rateofthefilteristoohigh,itmayresultinturbulenceand lower filtration effectiveness. Furthermore, the pressure drop mustbetakenintoaccount because ithasanimpact ontheamountofeffortneededtodrivethehydraulicfluid through the filter. High-pressure drop filters have a tendency to use more energy and have higher running expenses.

In conclusion, careful consideration of a number of elements, including filter performance, flow rate handling capacity,pressuredrop,andserviceintervals,isnecessary whenbuildinganeffectivefiltrationsystemforahydraulic system. Engineers can guarantee that the system runs dependably and efficiently while reducing downtime and maintenancecostsbyoptimisingtheseparameters.

Recent years have seen a substantial increase in interest in the use of conical filters for energy conservation in hydraulic systems. Conical filters have been optimised in several research to increase performanceanddecreaseenergylosses.

One study by Zhang et al. (2021) investigated the effect of conical filter geometries on pressure drop and filtration performance. The study found that increasing the cone angle of the filter increased the pressure drop, while decreasing the cone angle improved the filter's filtration efficiency. The optimal cone angle was found to be between 25-30 degrees, which provided a balance betweenpressuredropandfiltrationperformance.

K.S. Kansara and K.H. Wu presentedan optimization method for hydraulic filter design, taking into account factorssuchasfiltrationefficiency,pressuredrop,anddirt holdingcapacity,andappliesthemethodtoaconicalfilter designforheavy-dutyoff-highwayapplications.

J. R. Younce and T. L. Simonson presented an experimental investigation of the effect of different geometric parameters of conical filter elements on their performance in terms of filtration efficiency and pressure drop.

K. Y. Chiu, K. W. Wang, and C. Y. Huang presented the design of a hydraulic filter element with a conical mesh structure, aimed at improving the filtration efficiency and dirt holding capacity compared to conventional flat mesh filters.

R.H. Warring (1983) demonstrated that the fluid viscosityperformancecurvevariesforeachfiltertypeand size, and that the design and size of the overall filter rather than the element largely determines the relationshipbetweenpressuredropandflowrate.

RT. H. Peery and Cecil H. Chilton (1990) conducted research on the idea that the flow through a filter screen canbecomparedtotheflowthrougha numberoforifices simultaneously.

C. Contaldi, A. Maturo, and F. Oriani experimented on the performance of different hydraulic filter elements, including conical filters, in terms of filtration efficiency, pressuredrop,anddirtholdingcapacity

A.V.KozlovandA.N.Semenovpresentedanumerical solutionforfluidflowinaconicalfilterelement,analyzing the effect of different geometric parameters on the pressuredropandfiltrationefficiency.

Finally, it has been demonstrated that conical filters enhance energy conservation in hydraulic systems by lowering pressure drop and energy losses. Further study isrequiredtooptimisetheconical filterdesignforenergy conservation because the ideal filter shape, porosity, and mesh size can vary depending on the particular application.

2. IMPORTANCE OF SPECIAL TYPES OF FILTERS

Conical filters are of great importance in hydraulics duetotheiruniquedesignandfiltrationcapabilities.They have a conical shape, which enables a more uniform distribution of fluid flow across the filter's surface. This design reduces pressure drop and improves filtration efficiency, making them a highly effective choice for hydraulicsystems.

One of the primary functions of conical filters is to remove contaminants from hydraulic fluid, such as dirt, debris, and moisture. Contaminants in the hydraulic fluid cancausesignificantdamagetothesystem'scomponents, leading to system failure and downtime. By effectively filteringoutthesecontaminants,conicalfiltersensurethat thehydraulicfluidremainscleanandthesystemoperates efficiently.

Conical filters are superior to other types of filters, such as cylindrical filters, in terms of their ability to filter as well as their capacity to hold more dirt. The frequency of filter changes and related downtime are reduced since theycanholdmorepollutantsbeforeneedingreplacement or maintenance.

Conical filters are also a reasonably priced option for hydraulicsystems.

They are built differently than other types of filters, resulting in a reduced pressure drop, which lowers the energy needed to move hydraulic fluid through the system. Because of this energy efficiency, the system is moresustainableandhaslowerrunningexpenses.

Overall,becauseofitsdistinctivedesign,filtrationabilities, high dirt-holding capacity, and cost-effectiveness, conical filtersareacrucialpartofhydraulicsystems.

They are essential in ensuring that hydraulic systems run dependably and effectively, with the least amount of downtimeandmaintenanceexpenses.

3. CONICAL FILTER CONSTRUCTION

The conical-type filter tested at CWPRS, Pune is a filtrationsystemdesignedtoremovecontaminantsfroma fluid stream. This filter comprises of welded inclined plates,whichareplacedata5°anglewiththeaxispassing through the center of the inlet. The filter is attached to a flat plate at a 90° angle. The fluid flow enters the conicaltype filter through the inlet and then enters the filter element through the opening provided. As the fluid flows through the filter, the inclined plates cause the contaminantstoseparatefromthefluid,allowingtheclean fluidtopassthroughandthecontaminantstobetrapped. One important aspect of the conical-type filter is the flat platethatisattachedtoit.Thisplateactsasaresistanceto the flow of fluid, thus decreasing the velocity of flow and increasing the pressure upstream of the flat plate. This increase in pressure helps to ensure that the fluid flow is maintained at a consistent rate, which is essential for the efficientoperationofthefilter.

Overall, the conical-type filter is an effective and reliable filtration system that can be used in a variety of applications to remove contaminants from fluid streams. Its unique design, which includes welded inclined plates

and a flat plate, helps to ensure that the filter operates at peak efficiency, while also providing consistent and reliableperformanceovertime.

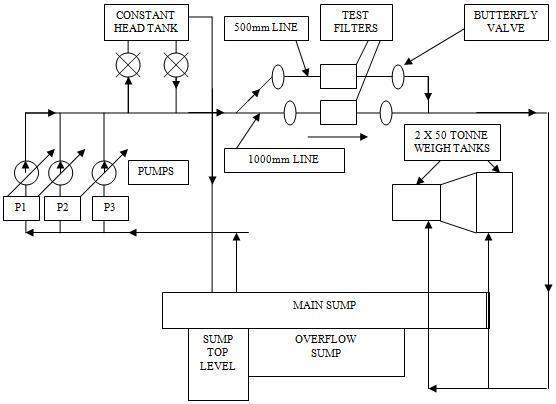
The test circuit at CWPRS, where the filter was put through its paces, complies with ISO: 4185 and provided an800m3capacitysumpthatservedasasourceofwater for three parallel, variable-speed DC motor-driven pumps (700 LPS, 30 mwc), which feed water at a constant flow rate either into the Constant Head Tank (CHT) or directly into the flow metre line. Two 1000mm-sized throttling valves are offered for series operation, providing a fine control for controlling the flow rate through the test element. Pumps with variable speeds and a throttle valve on the bypass line that connects the pump delivery manifold and suction manifold are additional controls for adjustingflowrate.

After passing through oneofthe test filter'sbranches, the flow enters a set of diverters that directs it in one direction to the sump and in another to the weigh tank. Additionally, it starts a high precision time counter that measures the length of time that water is diverted into a weighing system that consists of two weigh tanks, each with a capacity of 50 tonnes and mounted on load cells.

4. TEST CIRCUIT

In order to calibrate flow metres and determine the performance characteristics of other flow elements, such as valves and filters, the calibration laboratory at CWPRS, Pune, is outfitted with a primary gravimetric standard (Figure 2). The principle used in the circuit for flow measurement is to precisely weigh the amount of water passing through the flow element being tested at a constant flow rate over a precisely timed period. The fundamental way to determine flow rate is the mass of waterthathasbeendivertedtotime.

As a result, the time needed to gather the water in the weightankismeasuredwithaonemillisecondresolution. The net mass of water collected is the difference between the two mass measurements, or the original mass of the weigh tank before diversion of flow and the mass of the tankafterdiversionofflow.

5. INSTRUMENTATION

The details of instruments used and their accuracies areasfollows:

Flow-+0.3%bygravimetricmethod

Head-+0.1%byprecisionmanometer

Time-0.001secondwithdigitaltimer

Flowstabilityofcircuit-0.001%ofsetflowrate

Afiveandhalfdigit/timecounterwasusedtomeasurethe timeofdiversionintothemeasuringtank.Bychangingthe speed of the pumps or by adjusting valves that were mountedonthetestlinedownstreamofthefilter,theflow rate through the filter was adjusted to a desired value in thetestrangearoundthespecifiedflowrate.Therealflow ratewasmeasuredoncetheflowconditionhadstabilised. Near the rated flow rates as well as at different flow rate values,thepressureacrossthefilterwasmonitored.

6. CFD MODEL

The CFD model was set up using Ansys Fluent. The kepsilonmodelofturbulencewasemployed.TheReynolds-

averaged Navier-Stokes family of turbulence equations, whichmodelsallofturbulence'seffects,includesthetwoequationk-epsilonmodel.

Given that the model under consideration exhibits relatively small-scale flow phenomena and is predominantly characterized by straight flows, it can be inferred that the k-epsilon model is particularly wellsuited for simulating such flows. This is because the kepsilonmodelisknowntoperformwellincaseswherethe turbulence is relatively simple and the flow can be approximated as being isotropic and homogeneous. In suchscenarios,thek-epsilonmodelcaneffectivelycapture the dominant physical mechanisms responsible for turbulence and predict the fluid dynamics with a high degreeofaccuracy.

The mathematical model for the k-epsilon method is givenby:-

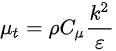
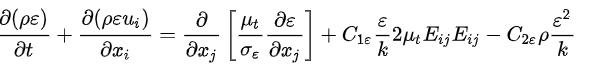
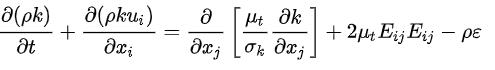
Forturbulentkineticenergyk, Fordissipation ε, Where,

is the velocity component in corresponding direction.

isthecomponentoftherateofdeformation.

istheeddyviscosity

Therestvaluesareconstantsandarepredefined.

Various vectors were set up for the computational fluid dynamics. The vectors were derived by analysing the workingconditionsofthefilter.

These velocity vectors represent the direction and magnitude of fluid flow at each point within the domain. Velocity vectors are used to track the movement of fluid particles and to identify regions of high or low flow.The velocityvectorwassetupinZ–axisandtherestaxeswere disabled.

Reynolds stress vectors describe the fluctuations in velocitywithinthefluidduetoturbulence.Reynoldsstress vectorsareusedtomodel theeffectsofturbulenceand to determinethelevelofmixingwithintheflow.Thevectors weresetupforobtainingfluctuationsinall3axes.

Vorticity vectors represent the local rotation of fluid particles within the domain. Vorticity vectors are often usedtoanalyzetheformationofeddiesorvorticeswithin the flow and to identify regions of high shear stress. The filter causes vortices in all 3 axes hence the respective vectorsweresetrespectively.

4. RESULTS AND CONCLUSION

The tests conducted on the divergent and convergent conical filters involved a comprehensive analysis of their filtering efficiency under different conditions. Specifically, thefiltersweretestedwith8Meshand40Meshvariations under both 100% clean and 50% clogged conditions. The purposeofthesetestswastoevaluatetheperformance of thefiltersintermsoftheirabilitytoremovecontaminants and to determine whether there were any noticeable differences between the divergent and convergent configurations. To support the experimental result, results, CWPRS also conducted CFD simulations using AnsysFluent.Thisapproachallowedthemtosimulatethe flow of fluids through the filters and to visualize the flow patterns under different conditions. The filter itself was designed using Creo Parametric, a powerful software packagethatiscommonlyusedforengineeringdesignand analysis

Overall, the combination of experimental testing and CFD simulations provided a comprehensive picture of the performance of the divergent and convergent conical filters.Theseresultscanbeusedtoinformthedesignand optimization of filtration systems in a range of industries, including water treatment, oil and gas, and pharmaceuticals.

To conduct the computational fluid dynamics (CFD) simulations, the filter assembly first meshed using Ansys Mesh. The housing of the filter was meshed using a quadrilateral mesh, while the filter itself was meshed using the tetrahedral meshing method. This combination of mesh types was chosen to ensure a high level of accuracy and efficiency in the simulations. Overall, the complete setup consisted of 17980 nodes, which were distributed across the various components of the filter assembly. The meshed components were then initialized and tested using Ansys Fluent, a widely used software package for CFD simulations. During the simulation process, the researchers monitored a range of variables, includingpressure,velocity,andturbulence,toanalyzethe behavior of the fluid as it passed through the filter assembly. These data were then used to calculate the

pressure drop across the filter in each configuration, as well astoevaluatetheoverall performance ofthefilter in terms of filtration efficiency and other key metrics. By using a combination of advanced meshing techniques and state-of-the-artsimulationsoftware,theCWPRSwereable togainvaluableinsightsintothe performanceofthefilter assembly and identify key factors that influence its behavior.

The rim of the filter was found to contribute to the pressure loss in both the divergent and convergent configurations. This may be due to the fact that the rim providesabarrierthatcreatesadditionalturbulenceinthe fluidflow,leadingtoincreasedfrictionandpressuredrop.

Understanding the specific factors that contribute to pressurelossindifferentfilterconfigurationsiscriticalfor optimizing filtration systems and ensuring their efficient operation. By identifying the sources of pressure loss, engineers and designers can develop strategies to minimize pressure drop and improve the overall performanceofthefiltrationsystem.

In addition to identifying the specific components of the filter assembly that contribute to pressure loss, the researchersalsoexploredtheeffectofvariousparameters on the performance of the divergent and convergent configurations. For example, they investigated the impact of mesh size and porosity on pressure drop and filtration efficiency.

Fig -3:Meshingdoneonthefilter

During the computational fluid dynamics (CFD) simulations, CWPRS observed a noticeable difference in the pressuredrop between the divergenceplacementand the convergent arrangement. Specifically, the pressure dropwasfoundtobegreaterinthedivergenceplacement than in the convergent arrangement. These findings are supported bythedata presentedinTable-1,whichclearly indicatesthevariationsinpressuredropbetweenthetwo configurations. It is worth noting that these results have important implications for the design and optimization of fluid systems, particularly in cases where minimizing pressuredropiscriticaltoachievingoptimalperformance. Furtherresearchwasconductedtoexploretheunderlying causesofthese observeddifferencesandtodevelop more effectivestrategiesforreducingpressuredropinthefilter.

The pressure loss in the divergent and convergent configurations was found to be influenced by different components of the filter assembly. Specifically, in the divergent configuration, the base plate was identified as themaincontributortothepressureloss.Thisislikelydue to the fact that the base plate provides a larger surface area for the fluid to pass through, which creates more friction and turbulence and ultimately results in a higher pressuredrop.

Ontheotherhand,intheconvergentconfiguration,the conical plate was found to be the primary source of gradient pressure loss. The conical shape of this plate causes the fluid to accelerate as it passes through the narrowest point of the filter, which leads to a drop in pressurealongthelengthoftheplate.

Their findings indicated that a higher mesh size and porosity generally resulted in lower pressure drop and improved filtration efficiency. However, it is worth noting that there may be a trade-off between filtration efficiency and pressure drop, as increasing the mesh size and porositycanalsoleadtoareductioninfilteringcapacity.

Furthermore, CWPRS found that the orientation of the filter assembly can also have an impact on its performance.Specifically,theyobservedthatchangingthe angle of the filter with respect to the flow direction can affect the distribution of flow and the resulting pressure drop.

Overall, these findings highlight the complex nature of filter performance and the need for a holistic approach to filtrationsystemdesignandoptimization.Byconsideringa range of factors, including component design, mesh size and porosity, and filter orientation, engineers and designers can develop more effective filtration systems that achieve optimal performance while minimizing pressuredropandotherundesirableeffects.

In the studies conducted it was found out that, the base plate and rim play a crucial role in determining the pressure drop across the filter. The base plate is the solid surface on which the filter media is mounted, while the rim provides the seal to prevent the bypass of the fluid aroundtheedgesofthefiltermedia.

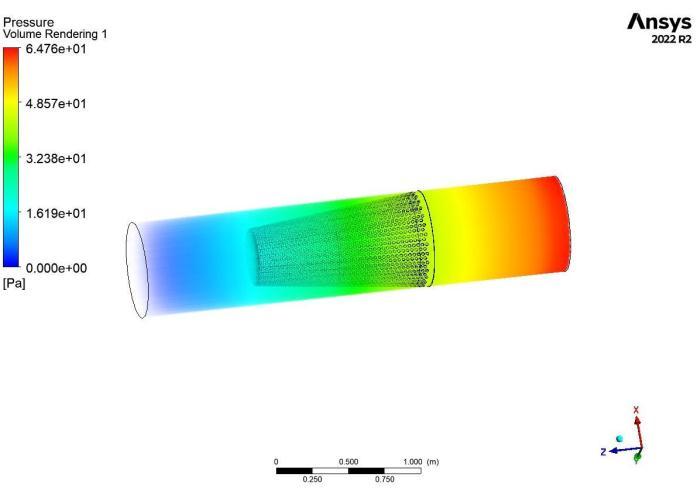
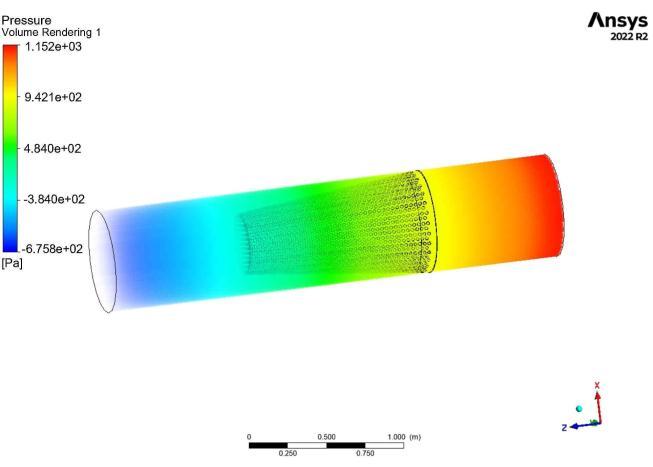
CleanCondition

Insummary,thebaseplateandrimofafilterplayacritical roleindeterminingthepressuredropacrossthefilter.The orientation of the fluid flow with respect to the filter mediamustbeconsideredinthedesigntoensurethatthe pressure drop is minimized, and that the efficiency of the filtration system is optimized. This is further highlighted intheCFDresults.

Inadivergentflow,thefluidflowisdirectlyperpendicular to the base plate, which results in the highest pressure dropacrossthefilter.Thisisbecausethefluidhastoflow through the narrowest part of the filter media, and the resistance offered by the filter is at its maximum in this orientation. Therefore, the design of the filter should take into consideration the orientation of the fluid flow to ensure that the filter media is not overloaded and to minimizethepressuredrop.

Incontrast,inaconvergentflow,thefluidflowissubjected to the gradient of the filter, which reduces the pressure drop across the filter. This is because the fluid flow is graduallycompressedasitpassesthroughthefiltermedia, which reduces the resistance offered by the filter. However, in convergent flow, the fluid flow eventually strikes the base plate, which can cause turbulence and resultinanincreaseinpressuredrop.

CloggedCondition

Whenafilterisinacloggedcondition,itsperformancecan beseverelyimpacted,and this isreflectedin the pressure drop across the filter. In the case of a clogged filter, the pressuredropisleastintheareawherethefilterissealed. This is because the area that is sealed does not allow any flow to pass through, resulting in a lower pressure drop comparedtotheotherpartsofthefilter.

RESULTSOBTAINEDBYTESTING(GravimetricMethod)

6. "Simulation of fluid flow in a conical filter element"byA.V.KozlovandA.N.Semenov

7. “Optimizationofhydraulicfilterdesignforheavyduty off- highway applications" by K. S. Kansara andK.H.Wu

8. "Effect of conical filter element geometry on hydraulic filter performance" by J. R. Younce and T.L.Simonson

9. "Hydraulic filter element with conical mesh for improvedperformance"byK.Y.Chiu,K.W.Wang, andC.Y.Huang

The results obtained from CFD simulations can show the areasofthefilterthataremostaffectedbyclogging.These areas may have higher pressure drops and may be more pronetodamageorfailure.

ACKNOWLEDGMENT

The authors are grateful to Dr R.S Kankara , Director CWPRS for giving guidance and permission to undertake the studies. The authors are thankful to Dr. Prabat Chandra,AdditionalDirectorCWPRSfortechnicalsupport and also thankful to colleagues who were associated with these investigations at various stages. The authors are gratefultoDr.Kkumarforguidanceandtechnicalsupport.

REFERENCES

1. Christopher Dickenson, T, “Filters and filtration Handbook,” Elsevier Advanced Technology, 4th edition,1997,UK.

2. Logsdon Gary S, “Filter maintenance and Operation Guidance Manual”, AWWA Research Foundation,2002,USA.‘

3. Peery RT. H. “Chemical Engineering Handbook”, 1990,UK.[5] Warring,R.H., “HydraulicHandbook, 8th edition, trade and Technical press Ltd”. 1983,England.

4. Asian Journal of Convergence in Technology Volume III, Issue III Research Paper by CWPRS scientistDr.KKumar

5. "Experimental analysis of hydraulic filter elements"byC.Contaldi,A.Maturo,andF.Oriani