Analysing the performance of Recommendation System using different similarity metrics

Analysing the performance of Recommendation System using different similarity metrics

2Associate Professor, Department of Computer Science and Engineering, GITAM University, Visakhapatnam, Andhra Pradesh, 530045, India.

3Professor, Department of Computer Science and Engineering, GITAM University, Visakhapatnam, Andhra Pradesh, 530045, India.

4Professor, Department of CS and SE, College of Engineering (Andhra University), Visakhapatnam, Andhra Pradesh, 530045, India

Abstract - Intoday'smoderneraofinformationtechnology, finding a favourite item in a large dataset has become an essential issue. So, there is a need for a more effective recommendation system with better performance. To achieve this, a Collaborative filtering recommendation system is proposed in this work. Here, the comparison is made with various similarity metrics like Pearson Correlation, Cosine Similarity, Jaccard Coefficient, MSD (Mean Squared Difference), Sorensen Dice Coefficient and SVD(SingularValueDecomposition)ontheMovielens100k dataset. It is observed that the Jaccard Similarity metric, compared to Pearson correlation and cosine similarity, producesbetteroutcomeswithimprovedaccuracyandless timecomplexity.

Key Words: Recommended System, Jaccard Index, Pearson Correlation, Cosine Similarity, Spearman rank Correlation, Sorensen Dice coefficient, Prediction, Recommendations.

1. INTRODUCTION

A type of system known as a recommendation system is utilizedforfilteringorsortinginformationwiththepurpose ofpredictingauser'spreferenceorratingforaspecificitem. Thesesystemsarecommonlyusedtoprovidesuggestions foritemssuchasbooks,TVshows,movies,music,andapps thatmaybeofinteresttoagroupofusers.

Togeneraterecommendations,thesystem analysesusers' past interests, which can be gathered either explicitly, throughuserratingsofitems,orimplicitly,bytrackinguser behaviour like purchasing history, browsing data, and downloadedapplications.Inaddition,thesystemmayutilize information from the user's profile, such as age, gender, nationality,preferences,andhabitsoftheirgroupofusers,to compareandpresentpersonalizedrecommendations.

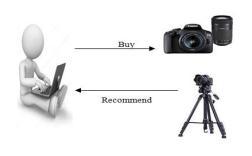
Fig.1. RecommendationSystem

In the depicted scenario, a user's purchase of a camera triggersarecommendationfromthesystemtopurchasea tripod.Therecommendationusestheuser'spreviousactions and preferences as a basis, which are used to suggest productsthatalignwiththeirinterests.Thisisanexampleof howrecommendationsystemsoperate.

1.1 Types

Intermsofrecommendationtechniques,thereexistvarious typesincluding:

Content-based:

Thistypeofrecommendationsystemreliesonuserreviews, ratings,andproductfeaturestogeneraterecommendations. Tofindsimilaritemstothosepreviouslylikedbytheuser, thesystemcalculatesthesimilaritybetweenitemsbasedon their associated features. The system then recommends items to users who have shown similar preferences. Recommendationsaregeneratedbyevaluatingsimilarities among items and considering the top-most regular items amongstneighbours.

Filtering

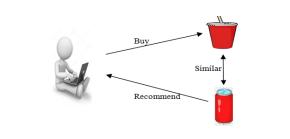
Inthegivenillustration,auser'spurchaseofjuiceprompts the recommendation system to suggest purchasing coke basedonthesimilarityoftheitems.Recommendationsare madebytakingintoaccounttheuser'spreviousbehaviour and preferences, demonstrating how content-based recommendationsystemsfunction.

Collaborative filtering:

Collaborativefilteringisastrategyusedtosuggestitemsto users by finding those with similar preferences and recommending items they have previously preferred. The system evaluates the similarity of users' preferences by examiningtheirratinghistory,alsoreferredtoas"people-topeoplecorrelation."Thisapproachiscommonlyemployedin Recommender Systems and is implemented using various methods.

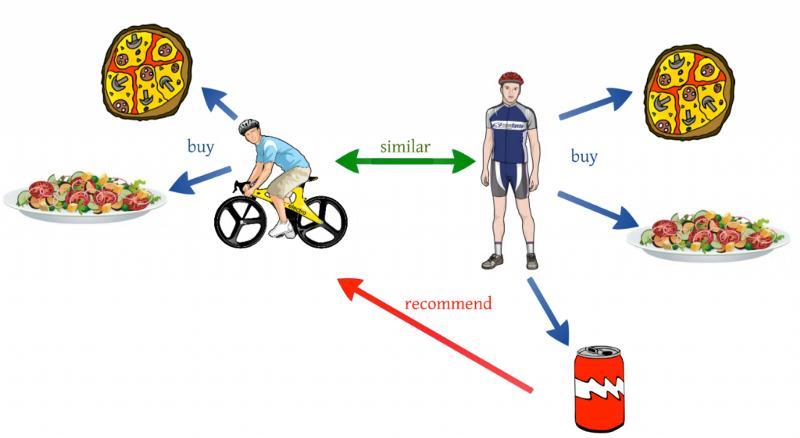
Neighbourhoodmethodsanditem-itemapproachesaretwo strategiesthatfocusontherelationshipsbetweenitemsor users in Recommender Systems. The item-item approach modelsauser'spreferenceforanitembasedontheirratings ofsimilaritems.However,thenearest-neighboursmethodis more widely used due to its efficiency, simplicity, and capacity to generate precise and personalized recommendations, particularly for smaller datasets. Additionally,avarietyofcollaborativefilteringalgorithms areavailabletoaccommodatelargerdatasetswithnumerous usersandagreaternumberofproductsthanitems.

Asshownintheabovefigure,UserAordersSaladandpizza, whileUserBlikestoorderSalad,pizzaandcoke.Bothusers haveorderedseveraltimesfromthesamefoodorderingapp and are given high ratings for their preferred items. The collaborative filtering system identified that User B has similarpreferencestoUser Aandsuggestedsomeoftheir favouriteitemstoUserA,whomaybemorelikelytoenjoy those items based on their past behaviour. Collaborative filtering helps to personalise the recommendations and makethemmorerelevantandappealingtoeachUser.Hence, thisishowthecollaborativefilteringrecommendedsystem works.

Hybrid recommender systems:

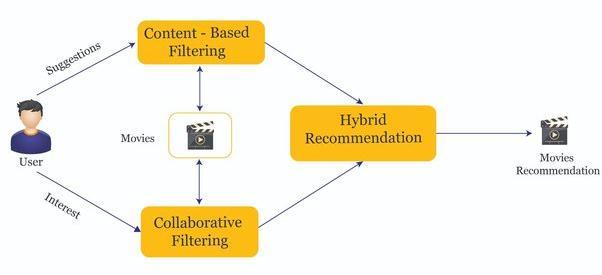
Recommender systems that combine content-based and collaborativefilteringtechniquesarereferredtoashybrid systems. This approach aims to take advantage of the strengthsofeachtechniquewhileaddressingitslimitations. The hybrid system works by using the strengths of one techniquetoovercometheweaknessesoftheother.

Forinstance,collaborativefilteringsystemsfacechallenges whenrecommendingnewitemsthatusersstillneedtorate. However, the content-based approach does not face this limitationsinceitreliesonitemfeaturesanddescriptions, whicharetypicallyreadilyavailable.Bycombiningthetwo techniques,thehybridrecommendersystemcanovercome thelimitationsofeachtechniqueandprovidemoreaccurate andpersonalisedrecommendationstousers.

As depicted in the preceding image, hybrid recommender systems utilize the advantages of content-based and collaborativefilteringmethodstoofferusersmoreprecise andvariedrecommendations.

1.3 Collaborative Filtering approach

User-to-User Collaborative filtering approach.

Theuser-to-userCollaborativeFilteringapproachiswidely used for generating recommendations based on the preferencesofotheruserswhosharesimilarinterestswith

thetargetuser.Itassumesthatuserswhohaveratedsimilar items in the past will likely rate future items similarly as well.

Togeneraterecommendations,thesystemfirstidentifiesthe most similar users to the target user based on their past ratings.Then,itconsiderstheratingsofthosesimilarusers for items that the target user has not yet rated to predict theirpotentialratings.Finally,thesystemgeneratesalistof top recommendations for the target user based on those predictedratings.

Inneighbourhoodalgorithms,thesystemselectsasubsetof userssimilartothetargetuserbasedonasimilaritymetric such as cosine similarity. The system then computes a weighted average of the ratings of those selected users to generate predictions for the target user. The weights assignedtoeachuseraretypicallybasedontheirsimilarity tothetargetuser.

Item-to-Item Collaborative filtering approach

The item-to-item Collaborative Filtering approach recommendsitemstousersbasedontheratingsthatusers have given to specific items. Instead of focusing on the preferences of other users, this approach analyses the similaritybetweenthetargetitemandthecollectionofitems thattheuserhasalreadyrated.

Togeneraterecommendations,thealgorithmusessimilarity measurestoidentifythekmostsimilaritemstothetarget item. It then computes the similarities and commonalities between the selected items to generate recommendations forthetargetuserbasedontheirpastratings.Thisapproach differs from the user-to-user Collaborative Filtering algorithm,whichfocusesonidentifyinguserswithsimilar preferencestothetargetuser.

As shown in Figure 5, there are two main approaches for generating recommendations: User-to-User and Item-toItemCollaborativeFiltering.

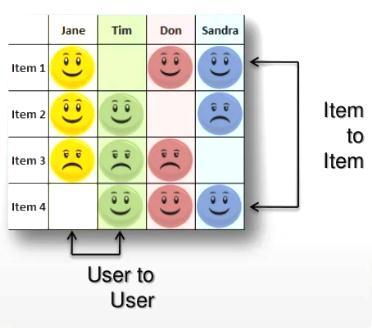
IntheUser-to-Userapproach,recommendationsaremade by identifying users who have similar preferences to the targetuser.Forexample,ifJaneandTimbothlikedItem2 anddislikedItem3,itsuggeststhattheymayhavesimilar tastes.Therefore,Item1mightbeagoodrecommendation for Tim. However, this approach may not be scalable for millionsofusers.

Ontheotherhand,theItem-to-Itemapproachrecommends itemsbasedontheirsimilaritytootheritemsthatusershave liked.Forinstance,ifTomandSandrabothlikedItem1and Item4,itsuggeststhatpeoplewholikedItem4willalsolike Item 1, and Item 1 will be recommended to Tim. This approachisscalabletomillionsofusersanditems,makingit apreferredchoiceforlarge-scalerecommendationsystems. Hence,theuser-to-userapproachcanbepracticalforsmaller datasetsbutcanbecomecomputationallyexpensivewhen dealingwithlargeamountsofdata.Incontrast,theitem-toitem approach is more scalable and can handle larger datasetsbyfocusingonitemsimilarity.

2. LITERATURE REVIEW

Resnick et al. [1] presented the user-to-user approach to collaborativefiltering,whererecommendationsforanactive useraregeneratedbyfindinguserswithsimilarhistorical ratingbehavioursandusingtheirratingsofitemsthat,the activeUserhasnotyetseen.Thesimilaritybetweenusers canbecalculatedusingvariousmetricslikecosinesimilarity orPearsoncorrelationcoefficient,whicharebasedon the users'historicalratingbehaviours.Afteridentifyingsimilar users, the weighted average of their ratings can be calculated,withtheweightsdeterminedbyhowsimilareach UseristotheactiveUser.

Breese et al. [2] proposed a prediction problem in collaborativefilteringandconductedanempiricalanalysisof prediction algorithms. The algorithm aims to predict the rating an active user will give an active item. To generate recommendations,thealgorithmreliesonhistoricaldataof ratingsandassociatedcontentofbothusersanditems.This data is used to make predictions about potential user preferencesanditempopularity.TheactiveUseristheUser for whom the prediction is made, and the active item is predicted. By analysing the logged data of user-item interactions,thesealgorithmsestimatetheratingtheactive Userwouldgivetheactiveitem.

InastudybyHerlockeretal.[3],theauthorsexploredthe critical decisions involved in evaluating collaborative filteringrecommendersystems.Theseincludedtheselection of user assignments to be evaluated, the types of analysis

anddatasetsused,andthemethodsofmeasuringprediction quality. To analyse the performance of different accuracy metricsonasingledomain,theauthorsreviewedprevious research and conducted their own experiments. They classified the different accuracy metrics into three equivalenceclassesandfoundthatthemetricswithineach classwerehighlycorrelated.However,theyalsofoundthat themetricsacrossdifferentclasseswerenotcorrelatedwith each other. The authors emphasized the importance of considering multiple evaluation techniques to provide a comprehensiveunderstandingofthesystem'sperformance.

InastudybyDeshpandeandKarypisetal.[4]proposeda methodforthemodel-basedrecommendationthatinvolves evaluating similarities between the items based on their attributes or features. They first identify how to calculate similarity between pairs of items using various methods, suchascosinesimilarityorPearsoncorrelationcoefficient. Subsequently,theyaggregatethesesimilaritiestocompute an overall similarity score between a recommended candidateitemandanitemtheuserhasalreadypurchased. By using this method, the system generates personalised recommendations for active users based on their past interactions.

Sarwar [5] conducted an analysis of different algorithms used for generating item-based recommendations. This analysisincludedexaminingtechniquesforcomputingitemitem similarities and strategies for obtaining accurate predictions. To evaluate the effectiveness of these algorithms, they were compared to the basic k-nearest neighbourapproach.Basedontheresultsofthestudy,itembasedalgorithmswerefoundtohavebetterperformancein terms of time compared to user-based CF algorithms. However,thestudyalsofoundthatuser-basedCFalgorithms provided better quality recommendations. The study highlightstheimportanceofconsideringbothperformance and recommendation quality when selecting an algorithm forgeneratingrecommendations.

Fkihetal.[6]reviewandcomparesimilaritymeasuresused inCollaborativeFiltering-basedRecommenderSystems.It categorises the most common similarity measures and providesanoverview.Theauthorsperformexperimentsto compare these measures using popular datasets and evaluation metrics. They find that the optimal similarity measuredependsonthedatasetandevaluationmetric.The paperalsorecommendsthemostsuitablesimilaritymeasure for each dataset and evaluation metric. This study is a valuable resource for researchers and practitioners in recommender systems who want to select the most appropriatesimilaritymeasuresfortheirCF-basedsystems.

Bell and Koren etal.[9]proposed a scalableapproachfor collaborativefilteringusingjointlyderivedneighbourhood interpolation weights. Their approach addressed the

limitationsoftraditionalcollaborativefilteringalgorithms, such as high computational costs and data sparsity, by deriving neighbourhood weights using a combination of user-to-user and item-to-item approaches. The proposed method was more accurate and scalable than traditional approachesonbenchmarkdatasets.Thepapercontributes to developing collaborative filtering algorithms for largescalerecommendationsystems.

Intheirstudy,Saranyaetal.[10]comparetheperformance ofvarioussimilaritymeasuresfortheCollaborativeFiltering (CF)technique.Foursimilaritymeasures,includingPearson Correlation Coefficient, Cosine Similarity, Mean Squared Difference,andAdjustedCosineSimilarity,wereevaluated usingtheMovieLensdataset.Thestudyaimedtodetermine whichsimilaritymeasureprovidesthebestperformancefor theCFtechnique.Theevaluationisbasedonthreemetrics: MAE,RMSEandPrecision.TheresultshowsthatthePearson Correlation Coefficient and the Cosine Similarity perform better than the other measures regarding accuracy and Precision. The study provides insights into selecting appropriate similarity measures for CF-based recommendationsystems.

3. Problem Identification & Objectives

3.1 Problem statement

The primary objective is to determine the most efficient methodofcomputingsimilaritybetweenusersanditemsin adataset.Varioussimilaritymeasures,includingtheJaccard coefficient, cosine similarity and correlation-based similarity,areusedtocalculatesimilarityandgeneratetop-N recommendationlists.Thegoalistoidentifywhichsimilarity measure offers the quickest and most efficient output for recommendingitems.

3.2 Motivation:

The increasing number of users on online sites such as Amazon and Netflix have led to a large user-item matrix, requiringtheefficientandquickgenerationofpersonalised recommendations. However, traditional collaborative filtering systems need help producing high-quality recommendations for users in the shortest time possible, especially for large datasets. Therefore, this study aims to comparetheefficiencyandadvantagesofdifferentsimilarity measures,includingtheJaccardcoefficient,cosinesimilarity, Pearsoncorrelation,MSDandadjustedcosinesimilarity,in generatingatop-Nrecommendationlist.

This study aims to identify the most efficient similarity measurethatcangenerateaccuraterecommendationseven for large datasets. User-based top-N recommendation algorithm is also explored as a potential solution to the challenges faced by traditional collaborative filtering

systems.Ultimately,therecommendeditemstousersshould satisfytheirpreferencesandinterests.

3.3 Objectives

Themaingoalsofthisstudyare:

1) To enhance the accuracy of the proposed recommendationsystem.

2) Toreducethetimecomplexityofthesystem.

3) To assess and contrast the performance of various

similaritymetricsinarecommendationsystem.

4) To identify the strengths and weaknesses of different similaritymetricsingeneratingrecommendations.

4. PROPOSED SYSTEM METHODOLOGY

The proposed system methodology uses a collaborative filteringapproach.Thesystemwillcollectandanalysedata from theuser’s profile,location, and interests. It will then determineparametersthatcanbeusedtocomparethisdata withothermembers'datainthedatabase.Thesystemwill search for similarities between users and other members, suchassharedinterestsorlocations.Thestepstoachieve thestudy'sobjectives:

Process:

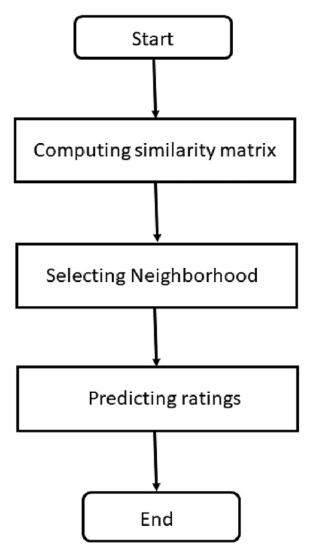
Tobuilda movierecommendersystemusinguser-to-user collaborative filtering method with the help of different similaritymetrics.

1) Prepare the data: Mergethemovieandratingdataintoa singledataframe,pivotthetabletocreateamatrixofusers and their movie ratings, and fill any missing values with zeros.

2) Compute user similarities: Calculate the similarity betweeneachpairofusersbasedontheirmovieratings.

3) Find similar users: identifyinguserswhosharesimilar preferencestothetargetuserbyselectingthekuserswith thehighestsimilarityscores

4) Predict ratings: Togenerateapredictionforeachmovie that a user has not yet rated, the algorithm calculates a weightedaverageoftheratingsgiventothatmoviebythek mostsimilarusers.

5) Generate recommendations: Recommend the top n movieswiththehighestpredictedratingstoeachuser.

Fig.6. FlowchartoftheCollaborative FilteringApproach

In Fig.6, it describes the flow of collaborative filtering approachanditsmajorfunctionality.

Theprocessflowdiagramdescribesthestepsinvolvedina recommendationsystemthatusestheKNearestNeighbour (KNN)approachtofindsimilarusersandrecommenditems tothem.Thestepsinvolvedare:

1) User Input: The user provides their User ID and some Factssuchasgender,age,andpincode.

2) Data Pre-processing: The raw data is pre-processed using NumPy and Pandas libraries. This step involves cleaningandtransformingthedataintoseparateframesthat canbeusedforfurtheranalysis.

3) K Nearest Neighbour (KNN): TheKNNapproachfinds similar users within a community/group. It involves selectingavaluefork(thenumberofnearestneighboursto consider)andcomputingthedistancebetweenusers.

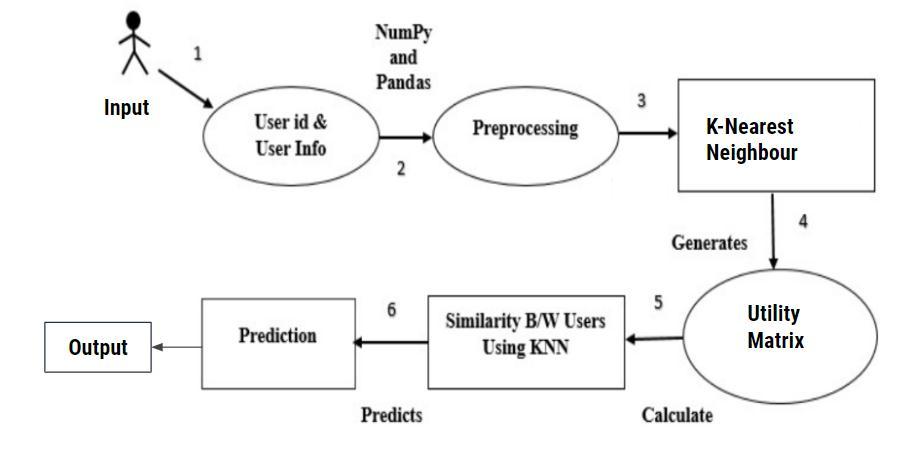
4) Utility Matrix: Autilitymatrixiscreatedafterapplying theKNNapproach.Thismatrixdefinestheaverageratingthe usergiveseachother.

5) User Similarity: User similarity is calculated using the utility matrix and Pearson correlation. This step involves calculatingthesimilaritybetweenuserstodeterminehow similartheirpreferencesare.

6) Recommendation: Thesystemusestheutilitymatrixand suggests items to the user based on the ratings of user’s similarity. The recommended items have received high ratingsfromsimilarusersbuthaveyettobeinteractedwith bytheuser.

Hence, the process flow diagram describes a recommendationsystemthatusescollaborativefilteringto recommenditemstousersbasedontheirsimilaritytoother userswithinacommunity/group.

Properties of similarity metrics

1)Non-negativity:Thesimilaritybetweenanytwoobjects mustbenon-negative.

S(X,Y)≥0forallXandY.

2)Symmetry:Thesimilaritybetweentwoobjectsshouldbe symmetric.

S(X,Y)=S(Y,X)forallXandY.

3) Reflexivity: Thesimilaritybetweenanobjectanditself shouldbemaximum.

S(X,X)=1forallX.

4)Triangleinequality:Thesimilaritybetweentwoobjectsx and z should be less than or equal to the sum of their similaritieswithathirdobjectY.

S(X,Z)≤S(X,Y)+S(Y,Z)forallX,Y,andZ.

5) Range normalisation: Similarity measures should be normalisedtoa certain range,often[0,1],tobecompared acrossdifferentdatasetsorapplications.

Similarity Metrics

Pearson Correlation:

PearsonCorrelationCoefficient(PCC)isusedtomeasurethe linearrelationshipbetweenthetwovariables.Inthecontext of recommendation systems, these two variables are the ratings two users give to the same items. The PCC value rangesbetween(-1,+1).Where,

-1=perfectlynegativecorrelation.

0=nocorrelation.

+1=perfectpositivecorrelation.

A positive value represents a positive correlation or a relationship in which two variables move in the same direction.Itisusedwhen

(1)Linearrelationship,

(2)Bothvariablesarequantitative,

(3)Normallydistributed

(4)TheyHavenooutliers.

Advantages of Pearson correlation coefficient

1) It is an accurate method of computing the correlation betweentwovariables.

2) The coefficient helps to determine the degree and strengthofthecorrelationbetweenthevariables.

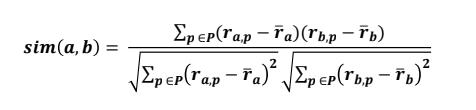
3)Itisstandardised,allowingfordirectcomparisonbetween differentdatasetsandvariables.

4)Itis robust tosmall amountsof noiseoroutliersin the data.

5) It can identify both positive and negative correlations betweenvariables.

Disadvantages of Pearson correlation coefficient

1)Pearson'scorrelationcoefficient(PCC)isunsuitablefor testingattributiveresearchhypothesesinvolvingonlyone variable.ItisbecausePCCisabivariatestatisticalmodelthat analysestherelationshipbetweentwovariables.

2)Itcannotdeterminethenonlinearrelationshipsbetween variables.

3) It does not distinguish between dependent and independentvariables.

4) PCC is sensitive to outliers in the data, which can significantlyaffectthecalculatedcorrelationvalue.

Cosine similarity:

Cosinesimilarityisapopularsimilaritymeasureutilizedin Collaborative Filtering to evaluate the similarity between

twosetsofratingvectors,whichcouldbetheratingvectors of two users or two items. It calculates the cosine of the anglebetweenthetwovectorsinamulti-dimensionalspace. By comparing the cosine similarity between two rating vectors, the Collaborative Filtering approach can identify userswhosharesimilartastesoritemsthatexhibitsimilar rating patterns. The cosine similarity score is bounded between -1 and 1, where a score of 1 represents identical vectors, -1 signifies diametrically opposed vectors, and 0 indicatesorthogonalorindependentvectors.

Advantages of Adjusted-cosine similarity

1)Overcomesthedrawbackofcosine-basedsimilarity

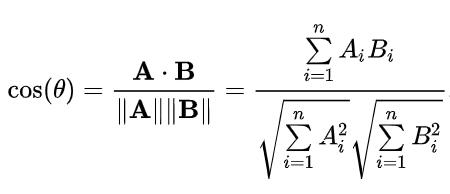
2)Itsubtractstheuseraveragefromeachco-ratedpair

3)Itconsidersthedifferencesinratingscalesacrossusers.

4) Iteffectivelyhandlessparsedata,wheremanyentriesin theuser-itemmatrixaremissing.

Advantages of cosine similarity:

1) Cosinesimilarityiscomputationallyefficientanddoes notrequirealotofmemory,whichmakesitsuitablefor largedatasets.

2) Itisscale-invariant,whichmeansthatitisnotaffected by the magnitude of the ratings, only their directions. Thispropertymakesitusefulforhandlingsparsedata anddatawithmissingvalues.

3) It is widely used in many applications, including text mining,imageanalysis,andrecommendationsystems.

Disadvantages of cosine similarity:

1) It does not take into account the magnitude of the ratings,onlytheirdirections.

2) Thiscanleadtoinaccuraciesifsomeuserstendtorate itemsmuchhigherorlowerthanothers.

3) It assumes that the ratings are distributed uniformly across all dimensions, which may not be the case in somedatasets.

4) It is sensitive to outliers, which can have a significant impactonthesimilarityscoresiftheyarenothandled properly.

Adjusted cosine similarity:

It is a modification of the cosine similarity measure that addressesitslimitations.InCollaborativefiltering,similarity betweenusersiscomputed based on the ratingmatrix. In contrast, in item-to-item Collaborative filtering, the similarityiscomputedbasedonthecolumns.However,the standard cosine similarity measure used in item-to-item Collaborative filtering does not consider user rating behaviourdifferences.

Spearman Rank Correlation

Spearman Rank Correlation is a similarity measure that computessimilaritybasedonrankingsratherthanratings, thuseliminatingtheneedforratingnormalization.However, thismethodisnotsuitableforincompleteorderings,evenif theratingsarecomparable.

Mean Squared Difference

TheMeanSquaredDifference(MSD)approachconsidersthe absolute ratings by calculating the mean of the squared differences between ratings instead of the traditional approachofconsideringthetotalstandarddeviations.This mean is used to determine the similarity between two vectors. A smaller value of the mean squared difference indicatesahighersimilaritybetweenthevectors.

Jaccard Similarity Coefficient:

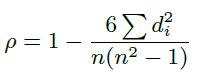
The Jaccard coefficient is a metric used to quantify the similarityand dissimilarity betweentwo sample sets. It is computedbydividingthesizeoftheintersectionofthesets by the size of their union. When both sets are empty, the coefficientis1.Thecoefficientrangesfrom0to1,where0 implies that there is no overlap between the sets, and 1 indicatesthatthesetsareidentical.

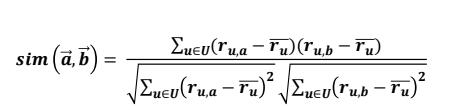
Where, J=JaccardSimilarity

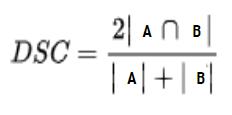
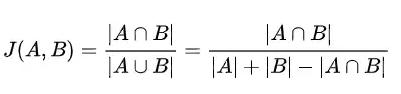
A=Set1

B=Set2

Advantages of the Jaccard Index:

1)Measuresthesimilaritybetweentwoasymmetricbinary vectorsorsets.

2)Thissimilaritymeasureisbeneficialwhenduplicates arenotnecessary.

Disadvantages of the Jaccard Index:

The Jaccard index has a significant disadvantage, mainly when applied to large datasets, as the data size strongly affectstheindex.Insuchcases,aslightchangeintheunion can significantly impact the index while keeping the intersectionthesame.

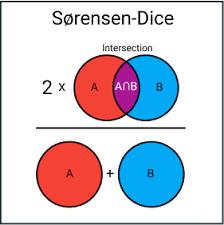
Sorensen–Dice coefficient:

TheSorensen-Dicecoefficientisasimilaritymeasureusedto comparesamplesets.ItisalsoreferredtoastheSorensenDiceindex,Dice'scoefficient,orDicesimilaritycoefficient. ThiscoefficientiscloselyrelatedtotheJaccardindexandis computedbydividingtwicetheintersectionoftwosetsby thesumoftheirsizes.

Sorensen-Dice index is more easily understood as the percentage of overlap between the two sets. This index is typically used to measure the similarity of two samples, particularlyinthecaseofdiscretedata.

Where

DSC=DiceSimilarityCoefficient

|A|,|B|=Thenumofelementsineachset.

|A∩B|=TheCommonnumofelements

Disadvantages of Sorensen–Dice coefficient:

1) Itweightseachitemdifferentlybasedonthesizeofthe relevantsetinsteadoftreatingthemequally.

2)Itdoesnotsatisfythetriangleinequality.Itisconsidered asasemi-metricversionoftheJaccardIndex.

4.3 Difficulty of the User-to-User Collaborative Filtering Algorithms

User-to-Usercollaborativefilteringalgorithmshavebecome popularinmanydomainsbuthaveseveralthingsthatcould be improved that make them more challenging to use effectively. These include sparsity in the data, scalability issues,lackofdiversityinrecommendations,thecoldstart problem,andprivacyconcerns.Whilethesealgorithmshave been successful, there is still a need to address these challengestoimprovetheiraccuracyandeffectiveness.

4.4 Proposed Improvement

Anapproachhasbeenproposedtoimprovethechallenges faced by user-to-user collaborative filtering algorithms. It analyses the user-item matrix using different similarity metrics to identify similarities and relationships among different products. The Jaccard index similarity metric providesmoreaccuraterecommendationstousersinless time.

Similarity measures like Pearson's correlation coefficient and cosine similarity are limited in their ability to make recommendations and are susceptible to the cold-start problem.Theproposedapproachusesco-relatedandnonrelated ratings to improve performance and enhance the qualityofrecommendations.

5. Implementation

TheSorensen-Dicecoefficientcomputesavaluebetween0 and1,where0representsnooverlapbetweentwosetsand 1indicatescompleteoverlap.UnliketheJaccardindex,the

This segment explains implementing a movie recommendationsystemusingPythonprogrammingwithK-

Nearest Neighbour. Implementing the system involves severalsub-sections:

Dataset: TheMovieLens100kdatasetisapopulardataset usedasastandardbenchmarkinthefieldofrecommender systems. It comprises 100,000 ratings of 1,682 movies, providedby943users.Theratingsarescoredonascaleof1 to5,with5beingthehighest.Demographicdataaboutthe users,includingtheirage,gender,occupation,andzipcode, isalsoincludedinthedataset,aswellasdetailsaboutthe movies,suchasthemovietitle,releaseyear,andgenre.

Data Cleaning: Beforebuildingthemodel,thedatamustbe pre-processedtocleanandtransformitintoausableformat. Itinvolveshandlingmissingdata,removingduplicates,and transformingitintoamatrixformsuitableforanalysis.

Model Analysis:Oncethedatahasbeencleanedandpreprocessed,itisnecessarytoanalyseittogaininsightsand determinetheappropriatemodel.Itinvolvesexploringthe relationships between variables, identifying trends, and selectingrelevantfeatures.

Model Building: In this case, the K-Nearest Neighbour algorithm predicts movie ratings based on similar users' preferences. The model is trained on the MovieLens 100k dataset, and its performance is evaluated using various metricssuchasRMSEandMAE.

Finally,themodelisusedtomakepredictratingsfornonrateditemsandtheresultsaredisplayedtotheuserinthe formofrecommendedmovies.

5.1 Technology

Python: It is a dynamically typed programming language used for web development, software, automation, data analysis, and visualisation. It is easy to learn and used by non-programmersforeverydaytasks.

NumPy: NumPyisaPythonlibrarythatenablesthecreation andmanipulationofmulti-dimensionalarraysandmatrices, with a rich set of high-level mathematical functions to facilitate tasks such as linear algebra, Fourier transforms, andarraymanipulation.

Pandas: A Python library for working with data sets, includinganalysis,cleaning,exploration,andmanipulation. Itprovidesfastandexpressivedatastructures.

Matplotlib: MatplotlibisaPythonlibrarythatfacilitatesthe creationofvisualizationsinvariousforms,includingstatic, animated,andinteractivegraphics.

Scikit-learn: Afreemachine-learninglibrarywithtoolsfor statisticalmodellingandmachinelearning.

Surprise: A Python library for building and evaluating recommender systems. It supports collaborative filtering andmatrixfactorisationtechniques,parallelprocessing,and hyperparametertuning.

Google Collaboratory: Google Collaboratory is a cloudbasedPythonIntegratedDevelopmentEnvironment(IDE) launchedin2017byGoogle,whichprovidesdatascientists with a platform to develop machine learning and deep learningmodels.Itofferscloudstoragecapabilitiestostore and share notebooks, datasets, and other files with collaborators.

6. Results and Discussions

6.1 Discussion

Example 1:SampleData(5*5)

Thesampledatasetconsistsofratingsforfiveitemsgivenby fiveuserswhereItem5isnotratedbyuserAlice.

Tab.1 User rating for 5 Items

Tab.1representstheuserratingsforfiveitems,whereAlice didnotprovidearatingforItem5.Thisstudyaimstopredict the rating for the non-rated item using the "User-Based CollaborativeFilteringApproach".Itusesdifferentsimilarity metrics, such as Pearson Correlation Coefficient, Jaccard Similarity Coefficient, and Sorensen Dice Coefficient, to determineusersimilarity.Basedonthesimilarityscore,the non-rateditemratingispredicted.

Similarity comparison

Tab.2 Users Similarity Comparison by using different similarity metrics

Tab.2comparesthesimilarityscoresbetweenAliceandthe other users in the data using three different similarity metrics:PearsonCorrelationCoefficient,JaccardSimilarity Coefficient,andSorensenDiceCoefficient.Thetableshows thatthesimilarityscoresbetweenAliceandUser1andUser2 arerelativelyhigh,indicatingastrongersimilarity.However, the Jaccard Similarity Coefficient and Sorensen Dice Coefficient give higher scores for Alice's similarity with User2andUser3.Basedonthesesimilarityscores,theKNN algorithmwillpredicttheratingforitem5.

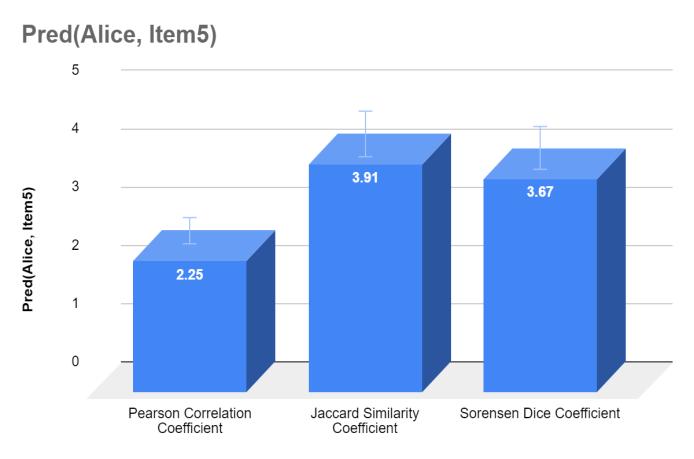
Tab. 3 shows that the predicted rating value for Alice and Item 5 is highest using the Jaccard Similarity Coefficient, followed by Sorensen Dice Coefficient, and then Pearson CorrelationCoefficient.

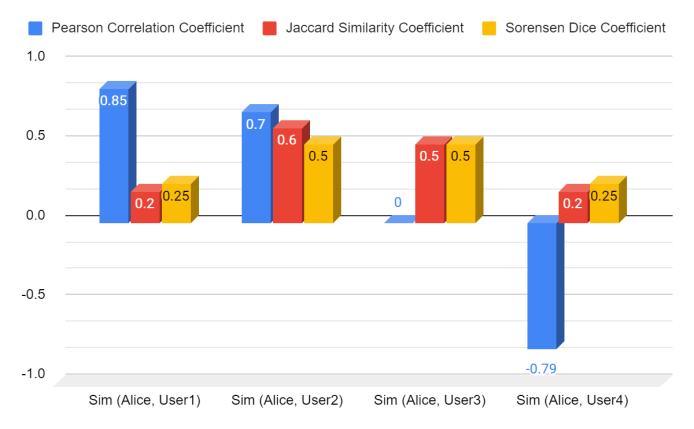
Infig.8,thex-axisshowstheusers,whilethey-axisshows3 the similarity score. Three different similarity metrics are used to calculate the similarity between Alice and other users. The bar chart shows that user 1 has the highest similarity score using the Pearson Correlation coefficient. Whereas, User 2 has the highest similarity score using Jaccard Similarity Coefficient. User 3 and user 4 have low similarity scores with Alice using Pearson Correlation CoefficientbuthaveaveragesimilarityscoresusingJaccard SimilarityCoefficientandSorensenDiceCoefficient.

InFig.9,acomparisonofthepredictedratingvaluesforthe non-rated item (Alice, Item 5) is presented using three different similarity metrics. The Jaccard Similarity Coefficientisobservedtoyieldthehighestpredictedrating valuefor(Alice,Item5),withavalueof3.91.

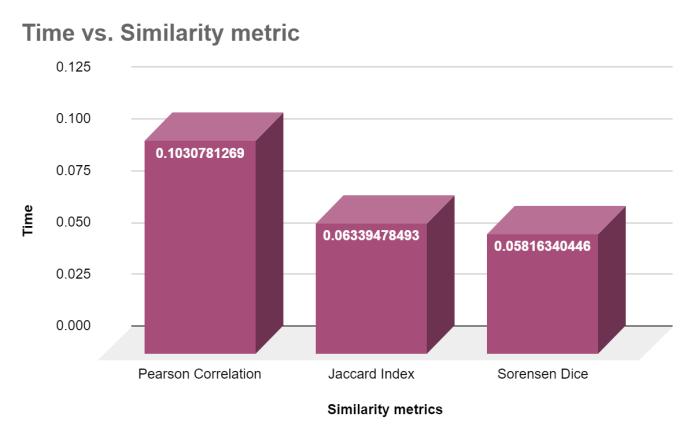
Fig.10 displays a bar chart where the x-axis shows the similarity metrics, and the y-axis shows time. The chart indicates that the Jaccard Similarity Coefficient takes less timethanthePearsonCorrelationCoefficient.

Example 2: Movielens100kDataset

TheMovieLens100Kdatasetiswidelyusedasa standard referenceforevaluatingcollaborativefilteringrecommender systems.Itcomprisesofratingsgivenbyuserstomovieson a 5-point scale, ranging from 1 to 5. The dataset contains 100,000 ratings and is made up of 943 unique users and 1682uniquemovies.Additionally,eachuserinthedataset hasratedaminimumof20movies.

When evaluating a filtering technique, statistical accuracy metricsareemployedtomeasureaccuracy.Thesemetrics directlycomparethepredictedratingswiththeactualuser rating.Commonlyusedstatisticalaccuracymetricsinclude Mean Absolute Error (MAE), Root Mean Square Error (RMSE),andCorrelation.

MAEisthemostpopularandwidelyused.Itmeasuresthe deviation of the recommendation from the user's specific value.

Tab.4comparestheRMSE(RootMeanSquaredError)and MAE(MeanAbsoluteError) valuesfordifferentsimilarity metrics. The metrics compared are Pearson Correlation, CosineSimilarity,JaccardCoefficient,MSD(MeanSquared Difference)andSVD(SingularValueDecomposition).

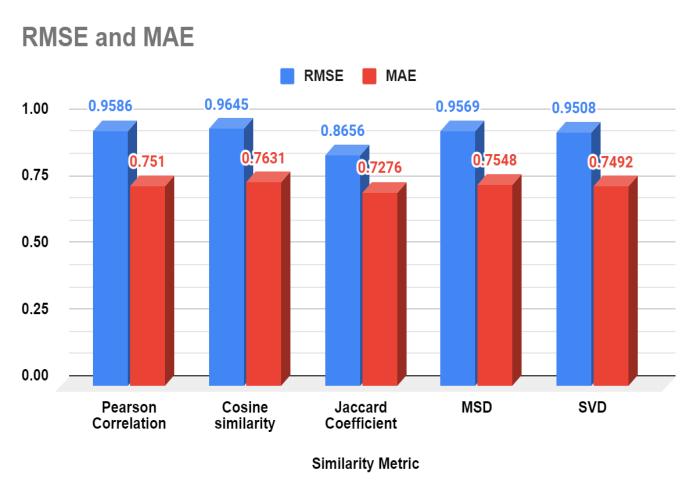
ThehighestvaluesforbothRMSEandMAEareobservedfor CosineSimilarity,followedbyPearsonCorrelationandMSD. ThelowestvaluesforbothmetricsareobservedforJaccard CoefficientandSVD.Hence, themetricswithhigherRMSE and MAE values indicate a larger prediction error, while lowervaluesindicatebetteraccuracy.

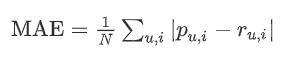
RootMeanSquareError(RMSE)metricgivesmoreweightto largerdeviationsinpredictionandisusedtoevaluatethe accuracyofrecommendationengines.ThelowertheRMSE value,thehighertheaccuracyoftheprediction.

6.2 Results : ComparisionTable

Fig.11 ShowsthebarchartcomparingRMSEandMAE valuesofdifferentsimilaritymetrics.

Fig.11 displays a bar chart showing Cosine Similarity's highestvaluesforRMSEandMAE.The JaccardCoefficient hasthelowestRMSEandMAEvalues,indicatingthatitisthe most accurate metric for predicting user-item ratings. However,thedifferencesbetweenthemetricsarerelatively small

Some of the Advantages of the Jaccard index:

TheJaccardindexhasseveraladvantages,including

1)Itcanmaketherecommendationsystemmorereliableby providingaccuratesimilarityscoresbetweenitemsorusers, whichcanthenbeusedtomakeaccuratepredictions.

2) It increases efficiency by reducing the number of comparisonstocalculatethesimilarityscoresbecausethe Jaccardindexonlyconsiderstheintersectionandunionof twosets,whichcanbecomputedefficiently.

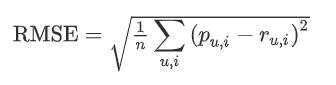
3) Execution is faster because it involves simple set operations,whichcanbecomputedquickly.

4) It gives accurate results when used appropriately, especiallyforsparsedatasetswithmissingratings.

TheJaccardsimilaritycoefficientperformswellintheuserbasedcollaborativefilteringapproachbecauseitfindsusers with similar preferences. It can help to predict accurate ratingsfornon-rateditems.

In the item-to-item collaborative filtering approach, the choiceofsimilaritymetricmaynotsignificantlyimpactthe predicted values because the focus is on finding similar itemsratherthanusers.However,theJaccardindexcanstill beausefulmetricinthiscontextbecauseitcanhelpidentify itemsthatarefrequentlyratedtogether,whichcanbeused tomakerecommendationsbasedonusers'ratingsofother items.

6.1 Comparison

Stitinietal.[31]Thepaper"InvestigatingDifferentSimilarity Metrics Used in Various Recommender Systems Types & Scenario Cases" explores the performance of different similaritymetrics.Theauthorsconductanempiricalstudy onfourtypesofrecommendersystems:user-to-user,itemto-item, content based, and hybrid. They compare the performanceofeightsimilaritymetrics:Pearson,Spearman, Cosine,Jaccard,Adjustedcosine,Euclidean,Manhattanand MeanSquaredDistance(MSD).

The study finds that the performance of the similarity metricsvariesfordifferenttypesofrecommendersystems and scenario cases. For user-to-user and item-to-item recommendersystems,CosineandJaccardsimilaritymetrics perform better than the other three metrics. For contentbased recommender systems, Pearson correlation and Cosinesimilarityperformthebest.Inhybridrecommender systems, the choice of similarity metric depends on the specificscenariocase.

Earlierstudiesonrecommendersystemscomparedvarious similarity metrics and found that the cosine and Jaccard metrics performed better than others in user-based recommendersystems.Thiscurrentpaperbuildsuponthat previousworkandconcludesthatthemodel'sperformance is optimal when using the Jaccard coefficient similarity metric.BasedonRMSE(0.8656)andMAE(0.7276)values, the Jaccard metric is shown to predict recommendations moreaccuratelythanallothersimilaritymetrics.

7. Conclusion & Future Scope

7.1 Conclusion:

Recommender/Recommendationsystemsarebecomingan essentialtoolforE-commerceontheweb.Theyhelpusersto finditemstheylikeandincreasesalesforbusinesses.With themassiveuserdatavolume,recommendersystemsneed newtechnologiestoimprovescalability.

This study presented and evaluated various similarity metricslikePearsonCorrelation,CosineSimilarity,Jaccard Coefficient,MSD(MeanSquaredDifference),SorensenDice Coefficient and SVD (Singular Value Decomposition) for User-to-usercollaborativefilteringrecommendersystems. TheresultsshowthattheJaccardindexcanperformwellfor large data sets while producing high-quality recommendations.

Hence,the Jaccardindex is useful when the data issparse and missing values are common. Its advantages include improvedreliability,increasedefficiency,fasterexecution, andaccurateresults.

7.2 Future Scope:

1)Enhancethesecuritymeasurestopreventfakeratingsor usermanipulation.

2) Enhance the evaluation approach for scenarios where therearenoratingsavailable.

 Adoptproactiverecommendationsystems.

 Utilize privacy-preserving recommendation systems.

3) Implement a Deep Neural Networks recommendation systemthatprovidesdynamicresults/recommendations.

8. REFERENCES

[1] Resnick, P., Iacovou, N., Suchak, M., Bergstrom, P., and Riedl, J. (1994). GroupLens: An Open Architecture for CollaborativeFilteringofNetnews.InProceedingsofCSCW '94,ChapelHill,NC.

[2] Breese, J.S., Heckerman, D., Kadie, C. (1998). Empirical analysisofpredictivealgorithmsforcollaborativefiltering. Proceedings of the 14th Conference on Uncertainty in ArtificialIntelligence.

[3]Herlocker, J.,Konstan,J.A.,Terveen,L.,Riedl,J.(2004). Evaluating collaborative filtering recommender systems. ACMTransactionsonInformationSystems(TOIS)22.

[4]Deshpande,M.,andKarypis,G.(2004).Item-basedtop-n recommendation algorithms. ACM Transactions on InformationSystem(TOIS),22(1),143–177.

[5]Sarwar,B.,Karypis,G.,Konstan,J.,andRiedl,J.(2001). Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th international conferenceonWorldWideWeb(pp.285-295).

[6] Fkih, F. (2021). Similarity measures for Collaborative Filtering-based Recommender Systems: Review and experimentalcomparison.JournalofKingSaudUniversity-

Computer and Information Sciences, 33(4), 431-449. https://www.sciencedirect.com/science/article/pii/S13191 57821002652?via%3Dihub

[7]D. Goldberg,D. Nichols, B.M.Oki, and D. Terry,“Using collaborative filtering to weave an information tapestry,” CommunicationsofACM,vol.35,no.12,pp.61–70,1992.

[8]ManosPapagelisandDimitris Plexousakis“Qualitative analysisofuser-basedanditem-basedpredictionalgorithms for recommendation agents” Engineering Applications of Artificial Intelligence 18 (2005) 781–789 www.elsevier.com/locate/engappai

[9] Bell, R., & Koren, Y. (2007). Scalable Collaborative FilteringwithJointlyDerivedNeighbourhoodInterpolation Weights. IEEE International Conference on Data Mining (ICDM’07),pp.43–52.

[10]Saranya,K.G.,SudhaSadasivam,G.,&Chandralekha,M. (2016). Performance Comparison of Different Similarity Measures for Collaborative Filtering Technique. Indian Journal of Science and Technology, 9(29), 1-7. DOI: 10.17485/ijst/2016/v9i29/91060

[11] A Case-Based Recommendation Approach for Market BasketDataAnnaGatziouraandMiquelSnchez-MarrIEEE INTELLIGENTSYSTEMS2015.

[12] Recommender Systems: An overview of different approachestorecommendationsKunalShah,AkshayKumar Salunke, Saurabh Dongare, Kisandas Antala SIT, Lonavala India2017

[13] Recommendation analysis on Item-based and UserbasedCollaborativeFilteringGarimaGupta,RahulKatarya, India

[14] Using collaborative filtering to weave an information Tapestry D. Goldberg, D. Nichols, B. M. Oki, and D. Terry, CommunicationsoftheACM,vol.35,no.12,pp.6170,1992

[15]Recommendersystems,Handbook,FrancescoRicci,Lior Rokach,BrachaShapira,PaulB.Kantor.Springer2010.

[16] Zhao, Zhi-Dan, and Ming-Sheng Shang. “User-based collaborative filtering recommendation algorithms on Hadoop.” In 2010 Third International Conference on KnowledgeDiscoveryandDataMining,pp.478-481.IEEE, 2010

[17] P. W. Yau and A. Tomlinson, “Towards Privacy in a Context Aware Social Network Based Recommendation System,” Privacy, Security, Risk and Trust (PASSAT) and 2011 IEEE Third International Conference on Social Computing (SocialCom), 2011 IEEE Third International Conference on, Boston, MA,2011, pp. 862-865. Doi:10.1109/PASSAT/SocialCom.2011.87

[18]Gao,Min,ZhongfuWu,andFengJiang.“Userrank for item-based collaborative filtering recommendation.” InformationProcessingLetters111,no.9(2011):440-446.

[19]Grcar,M.,Fortuna,B.,Mladenic,D.,Grobelnik,M.:k-NN versus SVM in the collaborative 3604iltering framework. DataScienceandClassificationpp.251260(2006).

[20] Hofmann, Collaborative filtering via Gaussian probabilisticlatentsemanticanalysis.In:SIGIR03:Proc.Of the 26th Annual Int. ACM SIGIR Conf. On Research and Development in Information Retrieval, pp. 259266. ACM, NewYork,NY,USA(2003).

[21]Bell,R.,Koren,Y.,Volinsky,C.:Modelingrelationshipsat multiple scales to improve the accuracy of large recommendersystems.In:KDD07:Proc.Ofthe13thACM SIGKDDInt.Conf.OnKnowledgeDiscoveryandDataMining, pp.95104.ACM,NewYork,NY,USA(2007)

[22]Wikipedialink

https://en.wikipedia.org/wiki/Collaborative_filtering

[23] Recommender Systems – The Textbook | Charu C.Aggarwal | Springer. Springer. 2016. ISBN 9783319296579.

[24]“AStudyofHybridRecommendationAlgorithmBased On User” Junrui Yang1, Cai Yang2, Xiaowei Hu3 2016 8th International Conference on Intelligent Human-Machine SystemsandCybernetics

[25]Gomez-Uribe,CarlosA.;Hunt,Neil(28December2015). “TheNetflixRecommenderSystem”.ACMTransactionson Management Information Systems. 6(4): 1–19. doi:10.1145/2843948

[26]AStudyofHybridRecommendationAlgorithmBased On User Xian University of Science and Technology Xian, China

[27] Crowe, N. (n.d.). Absolute bounds on set intersection and union sizes. Retrieved March 8, 2023, from https://faculty.nps.edu/ncrowe/intersect2.htm

[28]RecommenderSystemsinE-CommerceJ.BenSchafer, Joseph Konstan, John Riedl GroupLens Research Project DepartmentofComputerScienceandEngineeringUniversity ofMinnesotaMinneapolis,MN554551-612-625-4002

[29] Rajeev Kumar, Guru Basava, Felicita Furtado, "An Efficient Content, Collaborative – Based and Hybrid ApproachforMovieRecommendationEngine"Publishedin International Journal of Trend in Scientific Research and Development(ijtsrd),ISSN:2456-6470,Volume-4|Issue-3, April 2020, pp.894-904, URL: www.ijtsrd.com/papers/ijtsrd30737

[30]MaddaliSurendraPrasadBabu,andBodduRajaSarath Kumar.AnImplementationoftheUser-basedCollaborative Filtering Algorithm / (IJCSIT) International Journal of ComputerScienceandInformationTechnologies,Vol.2(3), 2011,1283-1286

[31] Stitini, O., Kaloun, S., & Bencharef, O. (2022). Investigating Different Similarity Metrics Used in Various Recommender Systems Types: Scenario Cases. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XLVIII-4/W32022, 327-334. doi:10.5194/isprs-archives-XLVIII-4-W32022-327-2022.

9. AUTHOR’S PROFILES

Kopanathi Sonali currently pursuing M.Tech- Data Science (CSE) from GITAM Institute of Technology,GITAM(Deemedtobe University), Visakhapatnam. Her areasofresearchworkaremachine learning and deep learning. Her areasofinterestareRecommended Systems,NeuralNetworksanddata science.

Dr.S.V.G.REDDY completedM-Tech (CST)fromAndhraUniversityand has obtained a PhD in Computer ScienceandEngineeringfromJNTU Kakinada. He is an Associate Professor, the Department of CSE, GIT,GITAMUniversity.Hisareaof research work is data mining, machinelearning and deep neural networks.HehasguidedvariousB. TechandM.Techprojectsandhas publicationsinseveraljournals.His areasofinterestaredrugdiscovery, computer vision, brain-computer interface,climatechangeandwaste management.

K. Thammi Reddy completed his PhD (computer science and engineering) during 2008 from JNTUHyderabad.Heisworkingas Professor,DepartmentofCSE,GIT and serving as Director, IQAC, GITAM University. His area of research work is data mining, machine learning and cloud computing with Hadoop. He has guided various B. Tech, M. Tech projects and had publications in several reputed journals and conferences.

V.ValliKumaricompletedherPhD (CSSE) from Andhra University during 2006. She is working as professor, Department of CSSE, college of engineering, Andhra University. Her area of interest is Software engineering, Network SecurityandCryptography,Privacy issues in Data Mining and Web Technologies. She has guided variousB.Tech,M.Techprojectsand hadpublicationsinseveralreputed journals and conferences. She receivedbestresearcherawardand othervariousawardsinthefieldsof teaching and research. She has undergone and completed various researchprojects.