IMPACT OF REDUCTION IN STIFFNESS OF SLAB ON THE BEHAVIOUR OF RCC STRUCTURE by IRJET Journal

IMPACT OF REDUCTION IN STIFFNESS OF SLAB ON THE BEHAVIOUR OF RCC STRUCTURE

Sneha S. Darekar1 , Prof. P. R. Barbude2 , Dr. S. A. Rasal3

1Post Graduate Student, Dept. of Civil Engineering, Datta Meghe College of Engineering, Airoli, Navi Mumbai 400708, Maharashtra, India

2Assistant Professor, Dept. of Civil Engineering, Datta Meghe College of Engineering, Airoli, Navi Mumbai 400708, Maharashtra, India

3 Assistant Professor, Dept. of Civil Engineering, Datta Meghe College of Engineering, Airoli, Navi Mumbai 400708, Maharashtra, India ***

Abstract – The various codes have suggested different values of stiffness modifiers for differentstructuralelementsin respect of serviceability and ultimate limit of the structure. The present work is carried out in order to incorporate the effect of crack section in structural analysis of the high-rise building (RCC) to attain the maximum resistance to earthquake loads and to protect building to some extent from earthquakes. A response spectrum analysis is carried out by using ETABS 18 software on four 3D models of same 32-story RCC building by considering the reduction in values of out of plane stiffness modifiers of all the slabs in each model, for the ultimate condition of the building. The results obtained are compared by considering parameters such as top storey displacement, story drift, major moment and required reinforcement percentage of shear walls at the base. According to analysis and design of model 4, it may be concluded that shear walls will be strengthened and welldesigned during seismic events and this will improve the seismic performance of the building.

Key Words: slabstiffness,stiffnessmodifier,cracksection effect

1. INTRODUCTION

Asheightofthebuildingincreases,havingadequatestrength andstiffnessisveryimportantforresistinglateralloadsand stabilityofthehigh-risebuilding.Contributionofstiffnessof structuralmembershasimpactontheoverallbehaviourof the building subjected to earthquake. For this study, the stiffness of slab (out of plane stiffness) is reduced further whilethestiffnessvaluesofremainingstructuralelements arekeptasmentionedinIS16700:2017.

In the present study a response spectrum analysis by ETABS 18 software is performed on four 3D models of 32-storyRCCbuildinginordertoincorporatetheeffectof crackapproximately,byfurtherreductioninstiffnessofslab element in each model for the ultimate condition of the building.

The Stiffness modifiers are the factors used to reduce stiffnessofconcretesectionsfortakingintoconsiderationthe

crackingofRCCsectionsinanalysisofthestructure.Stiffness modifiers are introduced to reduced moment of inertia of differentmembersduetocracking. TheTable-1showsthe stiffnessmodifiersgivenbythevariouscodesunderfactored loads.

Table -1: Stiffnessmodifiersgivenbydifferentcodes

Areaelementorshellelementhastwotypesofstiffnessesin planestiffnessandout-of-planestiffness.Inplanestiffness referredtoasf11,f22,f12andout-of-planestiffnessreferred toasm11,m22,m12.Inthisstudy,forslabelementtheinplane stiffness modifiers are taken as 0.25 as per Table 6crackedRCsectionpropertiesinIS16700:2017,Clauseno. 7.2,andtheoutofplanestiffnessmodifiersarereduced.Outof-planestiffnessmodifiersforslab areconsideredas0.25Ig (25%ofmomentofinertia)inmodel1,0.2Iginmodel2,0.1 Ig in model 3 and 0.01 Ig in model 4. For the remaining structural elements stiffness modifier values are taken as mentionedinIS16700:2017.

2. LITERATURE REVIEW

Theresearchworkwhichhasbeencarriedoutpreviouslyon stiffness reduction of reinforced concrete elements is reviewed.Aninvestigationofeffectofconcretecrackingon thelateralresponseofbuildingstructuresiscarriedoutby Ahmedet.al.(2008)(5).Theyexaminedtheeffectofconcrete crackingonitsstiffness.Theycarriedoutthepresentworkto study the quantitative effect of cracking and deflections amplificationontheresponseofRCCbuilding.Thebuilding

International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 10 Issue: 04 | Apr 2023 www.irjet.net p-ISSN: 2395-0072 © 2023, IRJET | Impact Factor value: 8.226 | ISO 9001:2008 Certified Journal | Page472

Codes StiffnessModifiers Slab Beam Column Wall IS16700:2017 0.25 0.35 0.7 0.7 IS1893:2016 - 0.35 0.7ACI318:2014 0.25 0.35 0.7 0.7 IS15988:2013 - 0.5 0.7 0.8

withdifferentaspectratioanddifferentrelativeheightare analyzed. They carried out analysis of structures using STAADPROsoftware.

Sang-Whan Han et.al. (2009) (6) developed equations for calculating slab stiffness reduction factor in the Effective beamwidthmodel(EBWM)withrespecttoappliedmoment (Ma)normalizedbycrackingmoment(Mcr)byconducting nonlinear regression analysis using stiffness reduction factors estimated from collected test results of 20 interior and10exteriorslab-columnconnectionspecimens.

D.P.N.Kontoni et.al. (2018)(11)performedatimehistory analysis by usingSAP2000software onthirteen modelsof 12-storyRCbuildingsinordertoillustratethecontributionof column stiffness and column cross sections (square or rectangular),beamstiffnessandslabstiffness,buildingfloor plans (square or rectangular) on building resistance to an earthquake. In order to investigate what percentage each typeofelementcontributestotheoverallperformanceofan high-rise building under seismic load, the stiffness of each type of element is reduced by 10% to 90%. From the literaturesurveyithasbeenobservedthat:

1. Slabstiffnesshasimpactonoverallbehaviorofbuilding subjectedtoearthquake.Inabsenceofstiffnessmodifiers, the structure would be stiffer and thus attract higher lateralforcesduetoearthquake.

2. Astheslabmomentduetolateralloadsincreases,more crackswill propagate intheslabsandtheslabstiffness willdecreaseduetocrackformation.Thus,thereduction in slab stiffness due to the effect of cracks should be reflectedintheanalysisofreinforcedconcretebuilding.

3. Ductile reinforced concrete structures experience large plasticdeformationsduringanearthquake.

4. Crackingduetoseismicshockaredifferentfordifferent configurationofstructureandtheirage.

5. Wecanincorporateapproximatelytheeffectofcrackin structuralanalysisofR.C.C.Buildingstofindresponsible response of the structure to ground movement by consideringvaluesofstiffnessmodifier.

3. MODELLING OF STRUCTURE

For the analysis high rise RC building, located in zone III havingirregularconfigurationintheplanofthebuildinghas been considered. The building comprising of Ground + 32 floors + Terrace. Total height of the building is 109.25 m fromfoundationtoterrace,withtypicalfloortofloorheight 3.05m.Totalplandimensionis36.7mx33m.Raftfoundation resting on rock/hard soil has been considered in the analysis. Structural system is a shear wall structure. A response spectrum analysis by ETABS 18 software was performedonfour3Dmodelsofsame32-storyRCCbuilding,

fortheultimateconditionofthebuildingi.e.underfactored loads. In the analysis of all four models only out-of-plane stiffness modifiers for slabs are changing and values of stiffnessmodifiersforotherstructuralelementsaresameas perIS16700:2017.

Model 1: Modelconsideringinplanestiffnessmodifiers(f11, f22,f12)&out-of-planestiffnessmodifiers(m11,m22,m12) forslabas0.25(asmentionedinIS16700:2017)

Model 2: Modelconsideringinplanestiffnessmodifiers(f11, f22,f12)forslabas0.25&out-of-planestiffnessmodifiers (m11,m22,m12)forslabas0.20

Model 3: Modelconsideringinplanestiffnessmodifiers(f11, f22,f12)forslabas0.25&out-of-planestiffnessmodifiers (m11,m22,m12)forslabas0.10

Model 4: Modelconsideringinplanestiffnessmodifiers(f11, f22,f12)forslabas0.25&out-of-planestiffnessmodifiers (m11,m22,m12)forslabas0.01

Figure 1 and 2 shows the mathematical model and the typicalfloorplanofETABSModel.

Fig-1: MathematicalModel

Thedetailsofthegradeoftheconcreteusedatvariousfloors aregiveninTable-2.

SeismicZoneFactor(Z) =0.16

ImportanceFactor(I) =1.2

ResponseReductionFactor(R)=4

4. RESULTS AND

The results obtained are compared by considering parameters such as top storey displacement, story drift, major moment and required reinforcement percentage of shearwallatbase.

Top Story Displacement:

Thedeflectionduetothedesignedlateralforceshouldnot exceed H/250, as earthquake is the governing factor. Therefore,themaximumpermissibleearthquakelimitinthis caseis109.25*1000/250=437mm

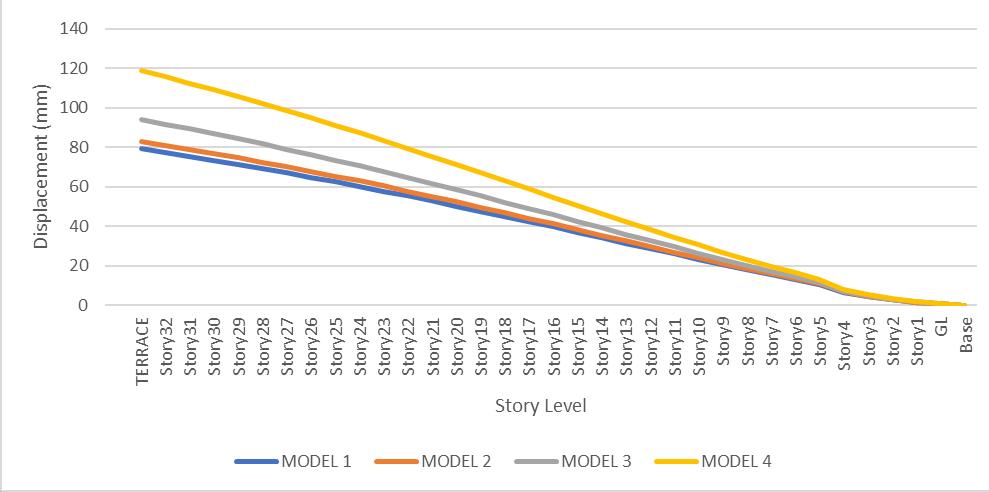
ThetopstoreydisplacementinXdirectionforallfourmodels is shown in Table-3. Also, the effect of top storey displacementinXdirectionispresentedinfigure3.

Structural Element CubeCompressiveStrength(fck)

Columns/ Shear

Walls

Beams andSlabs

Foundationto9th floor–60N/mm²(M60)

9th floorto20TH floor-50N/mm²(M50)

20th floortoTerracefloor-40N/mm²(M40)

Groundto9th floor-45N/mm²(M45)

10th floorto20TH floor-40N/mm²(M40)

21st floortoTerracefloor-30N/mm²(M30)

In the analysis, the floor slabs are assigned as shell (shell thin)elementandareconsideredassemirigiddiaphragms.

SteelReinforcementareThermo-MechanicallyTreatedbars.

Specified characteristic field strength (fy) is 500 N/mm². Modulusofelasticity(Es)is2.0x10^5Mpa.

BasicDesignWindSpeedis44m/sec.

DL=1.5to5.5KN/m^2(onvariousareasaccordingtousage)

LL=2to5KN/m^2(onvariousareasaccordingtousage)

SeismicloadsaredeterminedfromIS1893:2016(Part1),

Clauseno.7.6.2(a)basedonthefollowingparameters:

SeismicZone:III

ThetopstoreydisplacementinYdirectionforallfourmodels isshowninTable-4

Fig -2:TypicalFloorPlanofETABSModel Table -2: GradeofConcrete DISCUSSION

MODELNO. TopStoreyDisplacementInXDirection (mm) MODEL1 79.084 MODEL2 82.858 MODEL3 93.927 MODEL4 119.008

Table -3: TopStoryDisplacementinXDirection Fig-3: TopStoryDisplacementinXDirection

Also,theeffectoftopstoreydisplacementinXdirectionis presentedinfigure4.

Table -4: TopStoryDisplacementinYDirection

YDirection

Table3and4showsvaluesoflateraldisplacementattopof building due to earthquake in positive X and Y direction. FromthegraphsinFig3and4,itisobservedthatastheoutof-plane stiffness modifier of slab decreases the lateral displacementduetoearthquakeforcesinXandYdirection increases.

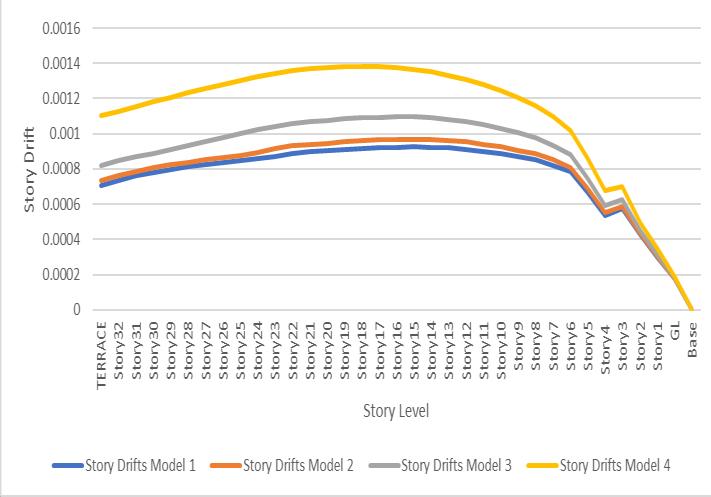
Story Drift:

Storydriftisthelateraldisplacementofastoryrelativetothe storybelow.Thestorydriftinanystoryduetothedesigned lateralforceshouldnotexceed0.004timesstoryheight(IS 1893-2002, clause 7.11.1). Story drift ratio is story drift dividedbythestoryheight. ThevaluesreportedinETABS are divided by story height. Therefore, the maximum permissibleearthquakelimitinthiscaseis0.004.

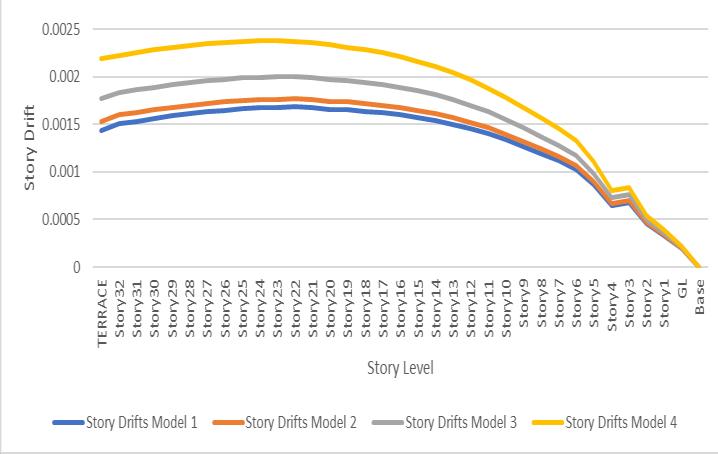
Table-5givesthevaluesofthestorydriftinXdirectionforall four models at different story level. Also the effect is illustratedinfigure5

MODELNO.

Displacementin

(mm) MODEL1 138.641 MODEL2 145.664 MODEL3 164.766 MODEL4 194.697

TopStorey

Fig-4:TopStoryDisplacementinYDirection

Story Level StoryDriftsinXDirection Model1 Model2 Model3 Model4 TERRACE 0.000707 0.000735 0.00082 0.001103 Story32 0.000736 0.000763 0.000845 0.001127 Story31 0.000761 0.000787 0.000868 0.001153 Story30 0.00078 0.000806 0.000888 0.001181 Story29 0.000796 0.000823 0.000909 0.001207 Story28 0.000811 0.000838 0.000932 0.001233 Story27 0.000824 0.000852 0.000955 0.001257 Story26 0.000836 0.000865 0.000978 0.001281 Story25 0.000848 0.000878 0.001 0.001304 Story24 0.000859 0.000896 0.001022 0.001325 Story23 0.000873 0.000915 0.001043 0.001344 Story22 0.000888 0.000931 0.00106 0.00136 Story21 0.000897 0.000941 0.00107 0.001369 Story20 0.000902 0.000946 0.001076 0.001374 Story19 0.00091 0.000954 0.001084 0.001379 Story18 0.000915 0.00096 0.00109 0.001381 Story17 0.00092 0.000965 0.001094 0.00138 Story16 0.000923 0.000968 0.001096 0.001375 Story15 0.000925 0.000969 0.001096 0.001365 Story14 0.000924 0.000968 0.001092 0.001352 Story13 0.00092 0.000963 0.001083 0.001333 Story12 0.000913 0.000954 0.00107 0.00131 Story11 0.000901 0.000941 0.001052 0.00128 Story10 0.000886 0.000925 0.00103 0.001244 Story9 0.00087 0.000907 0.001006 0.001204 Story8 0.000854 0.000887 0.000979 0.00116 Story7 0.000821 0.000852 0.000935 0.001096 Story6 0.000783 0.00081 0.000882 0.00102 Story5 0.000667 0.000689 0.000748 0.000861 Story4 0.000536 0.000552 0.000594 0.000675 Story3 0.000576 0.000589 0.000627 0.000702 Story2 0.000426 0.000434 0.000451 0.000495 Story1 0.000295 0.000301 0.000316 0.000347 GL 0.000178 0.000179 0.000182 0.000188 Base 0 0 0 0

Table -5: StoryDriftsinXDirection

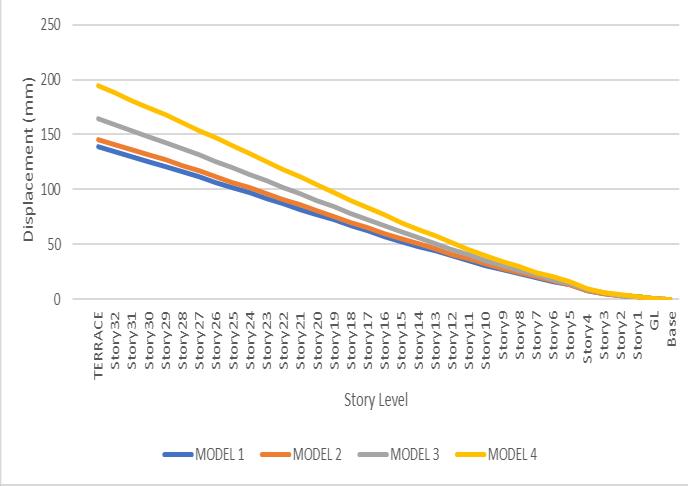
Fig-6:StoryDriftsinYDirection

FromtheTable5and6ithasbeenobservedthatastheoutof-planestiffnessofslabdecreasesthestorydriftsincreases. The values of story drifts are within limit. A comparative graphforMaximumstorydriftduetoearthquakeinXandY directionisshowninfigure5and6.

Shear wall moment at base:

Asstiffnessofslabdecreases,majormoment(M33)atbaseof some shear walls increases. Increasing moments in some shearwallsareshownhere.Table7,8and9givesmoments

Fig-5:StoryDriftsinXDirection Table-6givesthevaluesofthestorydriftinYdirectionforall four models at different story level. Also the effect is illustratedinfigure6.

StoryLevel StoryDriftsinYDirection Model1 Model2 Model3 Model4 TERRACE 0.001435 0.001524 0.001774 0.002189 Story32 0.001512 0.001598 0.001836 0.002227 Story31 0.001534 0.00162 0.00186 0.02255 Story30 0.001564 0.00165 0.00189 0.002283 Story29 0.00159 0.001676 0.001916 0.002308 Story28 0.001613 0.001699 0.001938 0.002328 Story27 0.001632 0.001718 0.001957 0.002345 Story26 0.001648 0.001734 0.001973 0.002359 Story25 0.001662 0.001748 0.001986 0.00237 Story24 0.001673 0.001759 0.001996 0.002377 Story23 0.001679 0.001765 0.002001 0.002378 Story22 0.001682 0.001768 0.002001 0.002372 Story21 0.001676 0.001761 0.001992 0.002357 Story20 0.001659 0.001744 0.001973 0.002334 Story19 0.001652 0.001734 0.001959 0.002311 Story18 0.001637 0.001718 0.001939 0.002283 Story17 0.00162 0.0017 0.001915 0.00225 Story16 0.001598 0.001676 0.001886 0.00221 Story15 0.001572 0.001647 0.001851 0.002162 Story14 0.00154 0.001613 0.001808 0.002107 Story13 0.001501 0.001571 0.001758 0.002042 Story12 0.001455 0.001521 0.001699 0.001967 Story11 0.0014 0.001463 0.00163 0.00188 Story10 0.001336 0.001395 0.00155 0.001781 Story9 0.001263 0.001317 0.001461 0.001674 Story8 0.001192 0.001241 0.001372 0.001569 Story7 0.001115 0.001161 0.001281 0.001457 Story6 0.001029 0.00107 0.001176 0.001331 Story5 0.000871 0.000902 0.000985 0.001106 Story4 0.000649 0.000671 0.000727 0.000809 Story3 0.000681 0.000704 0.000763 0.000838 Story2 0.000456 0.000469 0.000504 0.000546 Story1 0.000336 0.000344 0.000364 0.000392 GL 0.000196 0.000199 0.000204 0.000221 Base 0 0 0 0

Table -6: StoryDriftsinYDirection

atbaseofshearwallsW11(P13,P13A),W30(P63),W41(P51, P51A)respectivelyinallfourmodels.

From Tables 7, 8, 9 it is observed that as the out-of-plane stiffnessmodifierofslabdecreases,majormoment(M3)at baseofsomeshearwallsincreases.Theeffectisrepresented graphicallyinfigures7,8and9.

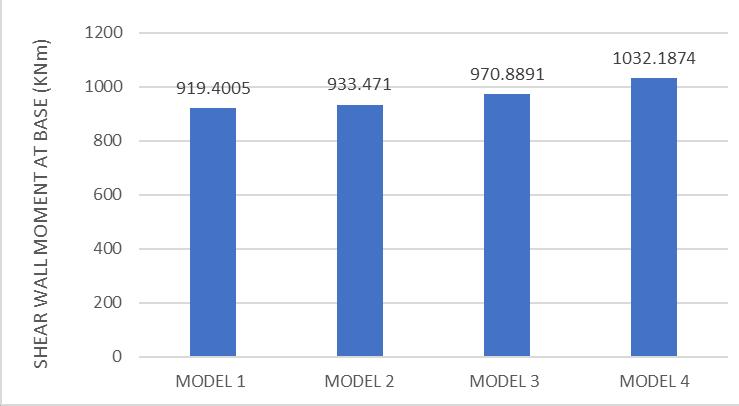
Table -7: MomentatBaseinShearWallW11(P13,P13A)

Pier

M3(KN-m)atGroundFloor

Fig-7:MomentatBaseinShearWallW11(P13,P13A)

Table -8: MomentatBaseinShearWallW30(P63) Pier

M3(KNm)atGroundFloor

Fig-8:MomentatBaseinShearWallW30(P63)

Table -9: MomentatBaseinShearWallW41(P51,P51A)

Pier Label M3(KNm)atGroundFloor

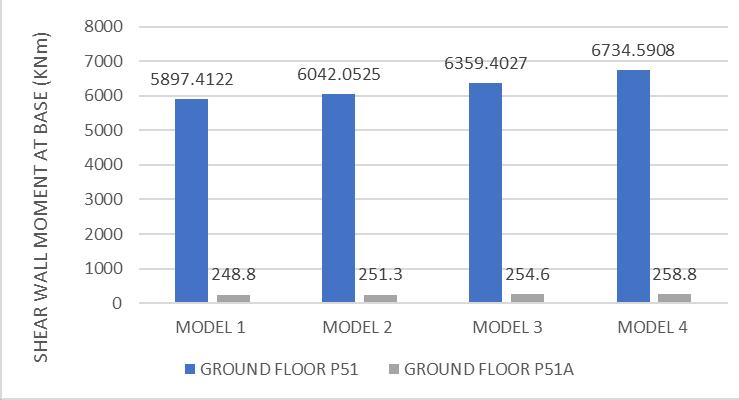
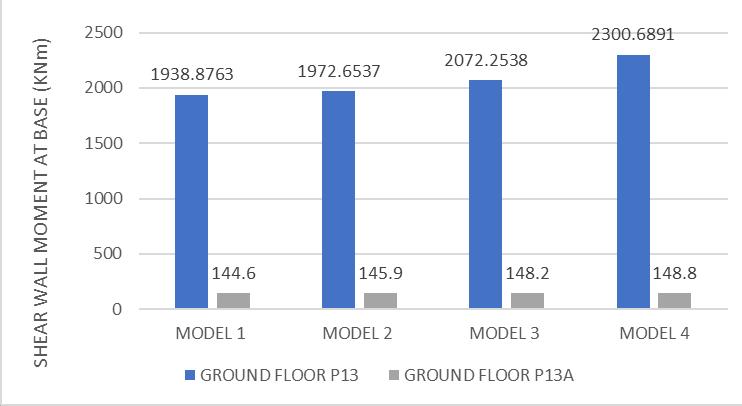
Fig-9: MomentatBaseinShearWallW41(P51,P51A)

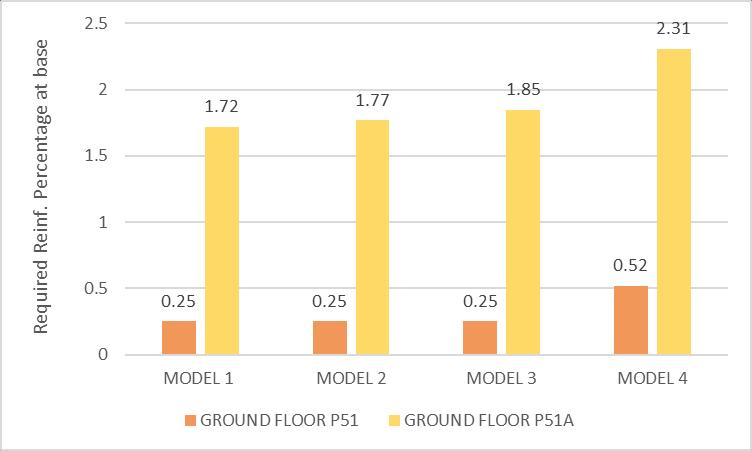
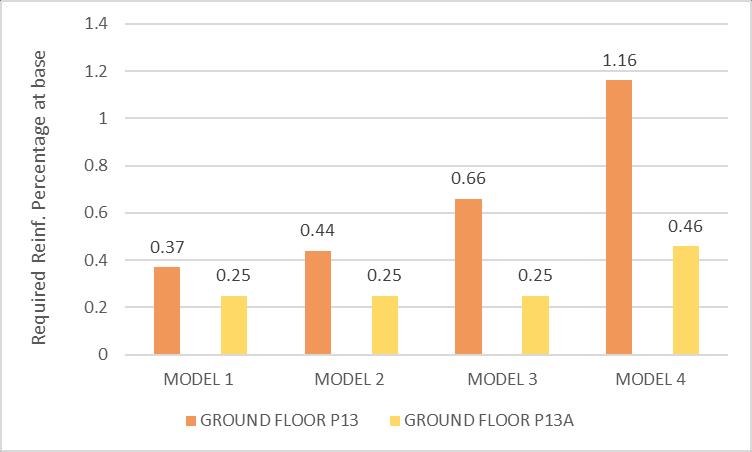
Required reinforcement percentage in shear wall at base:

Maximumrequiredreinforcement%inshearwalldepends on wind and earthquake loads anticipated at the location. Minimumrequiredreinforcement%inshearwallis0.25%. Graphshowsrequiredreinforcement%inaparticularshear wallatbaseinallfourmodels.

MODEL1 MODEL2 MODEL3 MODEL4 P13 1938.8763 1972.6537 2072.2538 2300.6891 P13A 144.6 145.9 148.2 148.8

Label

MODEL1 MODEL2 MODEL3 MODEL4 P63 919.4005 933.471 970.8891 1032.1874

Label

MODEL1 MODEL2 MODEL3 MODEL4 P51 5897.4122 6042.0525 6359.4027 6734.5908 P51A 248.8 251.3 254.6 258.8

Table -10: RequiredReinforcement%inshearwall W11(P13,P13A)atbase

From Tables 10 and 11 it is observed that as the stiffness modifierofslabdecreasestherequiredreinforcement%at baseofsomeshearwallsincreases.Hencesomeshearwalls shouldbestrengthenedbyadditionofsteelreinforcementto takehighermoments,sothattheyarenotunderdesignedin earthquake Figure10and11showsgraphicalrepresentation ofrequiredreinforcement%inshearwallsatbase.

5. CONCLUSIONS

From the present study following broad conclusions are drawn:

1. In the structural analysis of R.C.C. building model considered; effect of crack is incorporated approximatelybyfurtherreductioninstiffnessofslab element to attain the maximum resistance against earthquakes.

2. Stiffness modifiers are used to reduce out of plane stiffnessoftheslabelementbydecreasingmomentof inertiaupto20%,10%and1%.

3. Reducingoutofplanestiffnessofslabtolessthan10% theslabwillonlytransmitin-planeforcesandwillnot beabletocontributetoresistanybendingmoments.

Table -11: RequiredReinforcement%inshearwall W41(P51,P51A)atbase

4. Slabwillnottakepartinloadbearingandwholeload will directly transfer through the slab to supporting structural elements. Hence, beams located under the slabwillgeneratehighermoments.

Therefore,supportingstructuralelements(beams,shear walls) should be strengthened by addition of steel reinforcement to take higher moments, so that they are notunderdesignedinearthquake.

REFERENCES

[1] Park,R.,&Robertson,R.G.(1965).“Thelateralstiffness andstrengthrequiredtoensuremembraneactionatthe ultimate load of a reinforced concrete slab-and-beam floor”.MagazineofConcreteResearch,17(53),222–224. https://doi.org/10.1680/macr.1965.17.53.222

[2] Marti, P., & Kong, K. (1987). “Response of reinforced concreteslabelementstotorsion”.JournalofStructural Engineering, 113 (5), 976–993. https://doi.org/10.1061/(asce)07339445(1987)113:5 (976)

[3] Paulay, T. (2001). “A re-definition of the stiffness of reinforced concrete elements and its implications in seismic design”. Structural Engineering International, 11(1), 36–41.

https://doi.org/10.2749/101686601780324287

[4] Kim,H.-S.,&Lee,D.-G.(2005).“Efficientanalysisofflat slabstructuressubjectedtolateralloads”.Engineering

Pier Label RequiredReinforcement%inshearwallatbase MODEL1 MODEL2 MODEL3 MODEL4 P13 0.37 0.44 0.66 1.16 P13A 0.25 0.25 0.25 0.46

Fig-10:RequiredReinforcement%inshearwallW11(P13, P13A)atbase

Pier Label RequiredReinforcement%inshearwallatbase MODEL1 MODEL2 MODEL3 MODEL4 P51 0.25 0.25 0.25 0.52 P51A 1.72 1.77 1.85 2.31

Fig-11:RequiredReinforcement%inshearwallW41(P51, P51A)atbase

Structures", 27(2), 251–263. https://doi.org/10.1016/j.engstruct.2004.10.005

[5] Mohd,mohd&Khan,Dad&Wamiq,Muhammad.(2008). “Effect ofconcretecracking onthelateral response of RCC buildings”. ASIAN JOURNAL OF CIVIL ENGINEERING(BUILDINGANDHOUSING).9.25-34.

[6] Han, S.-W., Park, Y.-M., & Kee, S.-H. (2009). “Stiffness reduction factor for flat slab structures under lateral loads”.JournalofStructuralEngineering,135(6),743–750. https://doi.org/10.1061/(asce)st.1943541x.0000001

[7] Zhong,J.,Gardoni,P.,&Rosowsky,D.(2010).“Stiffness degradationandtimetocrackingofcoverconcretein reinforced concrete structures subject to corrosion.” Journal of Engineering Mechanics, 136(2), 209–219. https://doi.org/10.1061/(asce)em.1943-7889.0000074

[8] Vidović, D., Grandic, D., & Šćulac, P. (2012). Effective stiffness for structural analysis of buildings in earthquake. 4th International Conference Civil Engineering-ScienceandPractice.

[9] Yuan, H. J., Cao, L., & Deng, L. H. (2013). “Research on out-plane bending stiffness of multi-ribbed slab structure”.AdvancedMaterialsResearch,838-841,597–600.https://doi.org/10.4028/www.scientific.net/amr.8 38-841.597

[10] AthiraHaridasandS.ARasal(2022)“SeismicBehaviour of High Rise Building with Composite Shear Wall” International Journal of Innovative Research In Technology(ISSN:2349-6002),Volume8,Issue-11,pp 278–284

[11] HuzefaAttarwalaandS.A.Rasal(2022)“LateralDesign of Modern High Rise Structure Using Outriggers With Belt Truss System: An overview” Journal of Emerging Technologies and Innovative Research (JETIR) www.jetir.org Volume9,Issue4pp114-121

[12] Nguyen,M.C.,&Pham,P.T.(2017).“Aninvestigationon thebehaviourandstiffnessofreinforcedconcreteslabs subjectedtotorsion”.IOPConferenceSeries:Materials Science and Engineering, 164, 012017. https://doi.org/10.1088/1757-899x/164/1/012017

[13] Kontoni, D.-P. N., & Farghaly, A. A. (2018). “Stiffness effectsofstructuralelementsontheseismicresponseof RCHigh-RiseBuildings”.ArchivesofCivilEngineering, 64(1),3–20.https://doi.org/10.2478/ace-2018-0001

[14] Tena-Colunga, A., & Liga-Paredes, A. E. (2020). “Approximation of lateral stiffness for walls with two bands of openings considering slab stiffness effects” Journal of Building Engineering, 30, 101310. https://doi.org/10.1016/j.jobe.2020.101310

[15] SwikrutPatilandS.A.Rasal(2017),“BehaviourofBeamColumn Joint on Different Shapes of RC Framed Structures:AReview”,InternationalJournalofScience andResearch(IJSR).ISSN(Online):pp2319-7064,Vol. 6, issue-3, March 2017, www.ijsr.net, paper id: ART 20172238.

[16] Mithaiwala,M.E.,Patil,A.A.,&Khadake,D.V.(2020).“A ReviewonEffectofDifferentSetofStiffnessModifiers Varying Through Height of Structure on Analysis of Multi-Story R.C.C. Structure”. International Research JournalofEngineeringandTechnology(IRJET)Volume: 07Issue:08

[17] Aniket Kale and S.A. Rasal (2017), “Seismic and Wind Analysis of Multistorey Building: A Review” , International Journal of Science and Research (IJSR). ISSN (Online): pp 2319-7064, Vol. 6, issue-3, March 2017,www.ijsr.net,paperid:ART20172033.

[18] Gudmand-Høyer,T.(2004).“Stiffnessofconcreteslabs” Volume4.BYG.DTU.

[19] IS 456-2000, “Plain and Reinforced Concrete Code of Practice”, Bureau of Indian Standards, 4th revision, 2000.

[20] IS1893part1-2016,“CriteriaforEarthquakeResistant Design of Structure Part 1 General Provisions and Buildings”, Bureau of Indian Standards, 6th revision, 2016.

[21] IS 13920-2016, “Ductile Design and Detailing of Reinforced Concrete Structures Subjected to Seismic Forces-Code of Practice”, Bureau of Indian Standards, 1strevision,2016.

[22] IS 16700-2017, “Criteria for Structural Safety of Tall Buildings”,BureauofIndianStandards,2017.

[23] ACI318-19,“BuildingCodeRequirementsforStructural Concrete”,AmericanConcreteInstitute,2019.