MODIFIED GWO UPDATING PARAMETER FOR TUNING OF PITCH CONTROL OF FIXED SPEED WIND TURBINE
Aliyu Hamza SuleDepartment of Electrical Engineering, Hassan Usman Katsina Polytechnic, P.M.B. 2052, Katsina, Katsina State, Nigeria
Abstract - The Proportional and Integral (PI) controller found in the pitch control of the Wind Turbine has to be tuned to improve the pitch control performance. In this study, the updating parameter of the Grey Wolf Optimizer (GWO) was modified and the modified GWO was applied to tune the gains of the controller for improving the pitch control tuningresults. The controller tuning is formulated as the minimizationofthe Integral Time multiplied Square Error (ITSE) objective function under controller gains constraints. The modifiedGWO tuning results were validated through a comparison of its tuning results with that of GWO. The modified GWO exhibited faster convergence speed and provided better-tuned PI gains of the controller than the GWO. The faster settling time in pitch control of the Wind Turbine provided by the modified GWO can reduce the stress in the pitch control of the Wind Turbine compared to GWO
Key Words: Modified Grey Wolf Optimizer, updating parameter, tuning of pitch control, fixed speed wind turbine.
1. INTRODUCTION
The Grey Wolf Optimizer (GWO) is one of the populationbased algorithms which was developed by Mir Jalili [1]. It mimicstheleadershiphierarchyandhuntingstrategyofgrey wolves as one of the top predators in the food chain. The GWO applyits explorationand exploitation capabilities to findtheoptimalsolutiontoatuningproblem.Atthetopof thehierarchyofthewolvesistheαwolfwhichisthefittest wolfinthepacknormallyconsistingof5or12wolves.And nexttotheαwolfintheleadershiphierarchyistheβwolves which assist the α wolf. The δ wolves are the third in the leadershiphierarchy,andtheyshouldermoreresponsibility forsearchingforpreyandencouragingtherestofthewolves tofollowtheαwolf.Thelowestintheleadershiphierarchy arethe⍵wolves.Theirmovementsdependonhowtheyare instructedbythewolvesabovethemintheleadership[2]. One of the advantages of GWO is its simplicity. It only requires adjusting two parameters to overcome its nearoptimalconvergenceproblemandsharingknowledgeofthe searchspacebetweenitssearchagents.Also,adaptingthe values of vector A and operator a, ensures the efficient transitionofitsexplorationandexploitationbehaviour[1] However, the GWO has some limitations such as low accuracy and slow convergence speed [3] these led
researchers to conduct many studies to improve its performance.

TheaccuracyandconvergencespeedofGWOwasimproved by[3]throughthehybridizationofGWOwiththeModified DifferentialEvolution(MDE)algorithmtoformMDE-GWO. This improved the GWO search ability and local optimum avoidance.Theinfluenceofdominantwolvesinimproving thesearchingabilityoftheGWOwasstudiedin[4],where thedominantwolveswerevariedatthecommencementof every iteration. Furthermore, the dominant wolves were guidedbylearningdatainestablishingthethreedominant wolvesinthesubsequentgenerations.Thesemodifications of the GWO improved its performance in solving optimizationproblemsmorethanthestandardGWO.Thea andAparametersofaGWOweretunedin [5]toformthe modifiedGWO.Thisledtotheproperbalancebetweenits exploration and exploitation stages, consequently, the modified GWO to converged faster than the GWO. The authors[6]improvedthecapabilityofthefittestwolvesin thepacttooccupybetterpositionsduringiterations.Thisis achieved by balancing the exploitation and exploration stagesoftheGWO.Thesimulationresultshowsimproved performanceofAGCtunedwiththeModifiedGWOcompare withtheuntunedAGC.TheLévyflightandgreedyselection processes were embedded in the GWO [7] to modify its hunting stages This solves the problem of insuffient diversityofwolvesintheGWO.
Thelimitationofassigningalpha,betaanddeltawolveswith the same leadership superiority in the GWO updating positionmechanismwhichcontradictsthesocialleadership ofthewolveswassolvedin[3]throughhybridizationofthe GWO with Modified Differential Evolution to form MDEGWO.Itisobservedinthisstudytheupdatingmechanismof theGWO,wherethebestpositionsofAlpha(λ),Beta(β)and Delta (δ) wolves used to update the positions of the ω wolves,thethreebestwolveshaveequalinfluencesinthe updatingmechanism.Theequalinfluencehasviolatedthe social hierarchy of the wolves and the violation has the possibilityofnotprovidinganoptimalupdatingmechanism. Theobjectivesofthisstudyare:
1) TomodifytheupdatingparameteroftheGWO
2) To Formulate the transfer function of the closed-loop pitchcontrolsystemoffixed-speedWindTurbine.
3) TodeveloptheITSEobjectivefunctionforPIcontroller tuning in the pitch control of the fixed-speed Wind Turbine.
. The contribution of this study is the modification of updatingparameteroftheGWO,whichmodelstheupdating of wolves' positions from the best positions of α, β and δ wolves,andthisenhancedtheaverageconvergencespeedof the GWO. Furthermore, the modification of the GWO updating parameter provided better-tuned gains of the PI controllerinthepitchcontroloftheWindTurbinecompared to GWO. The structure of this paper consists of the introduction,principleofoperationofgreywolfoptimizer, methodology, results and discussion, conclusion, Acknowledgementandlistofreferences.
PRINCIPLES OF OPERATION OF GREY WOLF OPTIMIZER
The operation of GWO involved scouting, encircling and attackingpreybywolvesaredescribedinthissection.
Hunting the prey
Whilehunting,thegreywolvesidentifiedthepositionof thepreyandenclosedit.Thelocationsinthesearchspacefor thebestthreesolutionsto and gainsofthePIcontroller correspondtoα,βandδwolves.Theirpositionsrelativeto the prey position are presented in Equations (1) - (3). Equations(4)-(6)modelledthebestpositionsof and wolves from the prey, while Equation (7) represents the updating of positions of wolves from the positions of and wolves[8],[9]
Where isthedistanceofthewolvesfromtheprey, and arethepreyandgreywolfpositions,respectively.
Attacking and Searching for prey
Searching and attacking the prey correspond with the explorationandexploitationcapabilitiesofthegreywolves. The variable vectors and Equations, (9) and (8) are presented in Equations (10) and (11), respectively. If the valueofvectorAislessthan-1,thegreywolveswillattack theprey.Otherwise,theywouldsearchforabetterone.
Whenthewolvesarenearingtheprey,thisisequivalent tovaryingtheoperator from2to0,whilethevector is reducedtoa.Theoperators and liedbetween0and1.
METHODOLOGY
Themethodologyispresentedinthissection.
Description of PI pitch control of Wind Turbine

TheWindTurbineaerodynamicpowercanbecontrolled using different types of control methodologies. The dominant one is the PI controller pitch angle control[10] ThepitchcontrolsystemconsistsofthePIcontroller,pitch actuator, rate limiter and angle saturator. It is applied to limittheWindTurbine'smechanicalpoweroperatingaboveratedwindspeedtoratedpower[11]and[12]. Thecontrol objectiveistoadjustthepitchanglesothattheaerodynamic power is limited to rated power using the control law expressedbyEquation(12)[13], [14]
WhereKpand KIareproportionalandintegralgainsofthePI controller in the aerodynamic power control loop of the pitch control. While Pmec and Pnom are Wind Turbine aerodynamicpowerandnominalpower,respectively.
Encircling prey
The prey's encircling by the grey wolves is modelled usingEquations(8)and(9).
WhentheWindTurbine'spitchangleincreases,itleads tothelimitingofitsaerodynamicpowertotheratedvalue becauseofthenon-linearinverserelationshipbetweenthe pitchangleβandthepowercoefficientCp (λ,β)oftheWind Turbine.Atfullloadoperatingregion,thegeneratorofthe WindTurbinerunsattheratedspeedtogeneratetherated electricalpower .
Structure of the Optimization of PI pitch control of Wind Turbine.
TheblockdiagramoftheproposedOptimization-PIpitch controlstructureoftheWindTurbineisshowninFigure1.
ItconsistsofthePIcontroller,thepitchactuator(servomotor),andtheWindTurbineallconnectedinseries.Inthis study, the GWO and RGWO are proposed to fine-tune the gainsofthePIcontrollerinpitchcontrolofthewindturbine. DuringPIcontrollertuning,theGWO/RGWOtuningblockin Figure 1is responsible for tuning thecontroller'sgains. It continues to tune the gains of the PI controller while minimizingtheITSEofthepowererror ofEquation(13)at the input of the PI controller. The power error is the difference between the aerodynamic power ( ) of the WindTurbineanditsnominalpower( ).ThePIcontroller provides the pitch angle in mechanical degree presentedinEquation(14)tothepitchactuator.The drivesthepitchactuatortoobtain presentedin Equation(15),therequiredadjustmentofpitchangletothe rotorbladesoftheWindTurbine[15]
The transfer functions of the PI controller and pitch actuator are presented in Equations (16) and (17) respectively.TheFixedSpeedWindTurbineispresentedas asecond-ordertransferfunctioninEquation(18).Referto formethodofobtainingtheWindTurbinetransferfunction [16].Sincethosetransferfunctionsareforseriallyconnected components shown in Figure 2, their equivalent transfer functionispresentedinEquation(19).
WhereKistheopen-loopforwardgainoftheWindTurbine, isitsdampingratio,ωn isthenaturalfrequencyparameter andKp andKI aretheProportionalandIntegralgainsofthe PIcontroller.

Standard Objective Functions forControllerTuning







TheRGWOandtheGWOaremeta-heuristicalgorithms thatcanbeappliedasinstrumentsforcomputingthegainsof controllers in tuning problems. The standard objective functionsusedbyresearchersfortuningthegainsofthePI controller are the Integral Absolute of Error (IAE), the IntegralmultipliedTimeSquareofError(ITSE),theIntegral Square of Error (ISE), and the Integral Time multiplied AbsoluteofError(ITAE)[17],[18]. Thesearepresentedin Equations(20)-(23).
Formulation of the TransferFunction of the closedloop Pitch Control of Wind Turbine
ThefirststepintheproposedGWO/RGWOoptimizations forthePIcontrollerinthepitchcontroloftheFixedSpeed Wind Turbine is to formulate the transfer function of the closed-loopsystemconsistingofthecontroller,pitchcontrol and the Wind Turbine shown in Figure 2. It is a negative closed-loopsystem.
Where e(t) is the power error at the input of the PI controller, T is the simulation time, t is the instantaneous time,anddtisthesamplingtime.
Formulation of ITSE Objective Function for PI pitch Controller Tuning

Theobjectivefunctionisbasedonthepowererrore(t)at theinputofthePIcontrollerintheclosed-looppitchcontrol of Figure 3.6. The power error is already presented in Equation (13). Then the time domain power error was transformedintothes-planeusingtheLaplaceTransform andispresentedinEquation(24).Thepowererrorinthesplane of Equation (24) was utilized to develop the ITSE standardobjectivefunctionusedtotunethegainsofthePI controllerinthepitchcontrol.Thetuningismodelledusing Equation(25)tominimizeasingleobjectivefunctionMin: ITSEwithboundedEquationconstraints(26).
TheequalinfluencesofAlpha(λ),Beta(β)andDelta(δ) wolves in Equation (7) which model the updating of the positionsofwolveshaveviolatedthehierarchyclassofthe wolves and this has the possibility not to provide optimal tuningresults.Therefore,thevectorsum of , and wolves in the numerator of Equation (7) is modified by taking the square root of the sum as presented in Equation (27). The numeratorofEquation(7)wasreplacedwithEquation(27) toobtaintheResultantGreyWolfOptimizer(RGWO).
Optimal tuning of PI controller in pitch control
WhereTisthesimulationtime,tistheinstantaneoustime, anddtisthesamplingtime.
TheboundedconstraintsforthePIcontroller'soptimal tuningaretheupperandlowerboundsof thecontroller's ProportionalandIntegralgains.
Modifying the GWO updating parameter.
Theperformanceofmetaheuristicalgorithmsdependson tuning and control of their parameter [5] tuning and parametercontrol.Theupdatingpositionsofwolvesfromthe bestpositionsofAlpha(λ),Beta(β)andDelta(δ)wolvesis illustratedinFigure3.
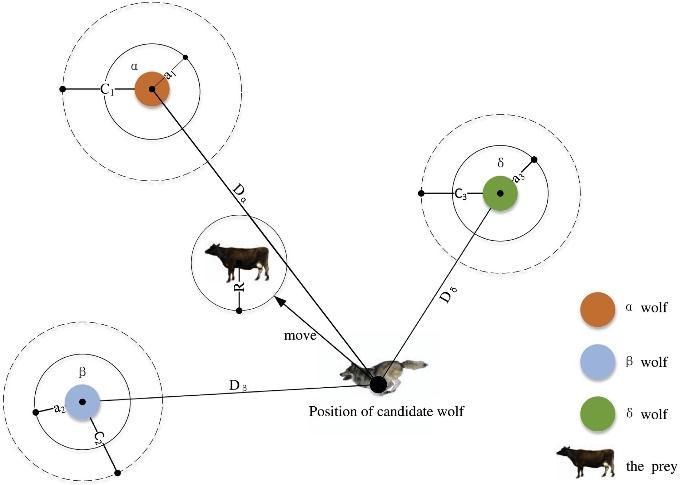
In this study, the GWO and RGWO were applied to tunethePIcontrollerinpitchcontrolofthethreemegawatts Squirrel Cage Induction Generator (3MW SCIG) Wind Turbine (see appendix). The number of variables to be optimized (dim)is 2, thatis the PI gains.Five number(5) wolveswereusedtofine-tunethegainsofthecontrollerby minimizing the ITSE objective function in 30 maximum number of iterations. The lower and upper bound constraintsweresetto0and25respectively.
Selected Parameters and Operators of the GWO and modified GWO.
TheselectedparametersandoperatorsoftheGWOand theRGWOalgorithmsforthefirstsearchspace[0,25][0,25] of and gains,selectedfortuningthePIcontrollerin pitchcontroloftheWindTurbinewerepresentedinTable1. ToruntheGWOandRGWOcodesforoptimaltuningofthe PI controller in the Wind Turbine pitch control, the controller'sproportionalandintegralgainsmustbeassigned as the position vectors, while the ITSE is assigned as the objective function. The GWO and RGWO execute steps to computethePIcontroller'soptimalgainswhilereducingthe power error at the controller's input with its upper and lowergainboundsasconstraints.
TUNING RESULTS AND DISCUSSION
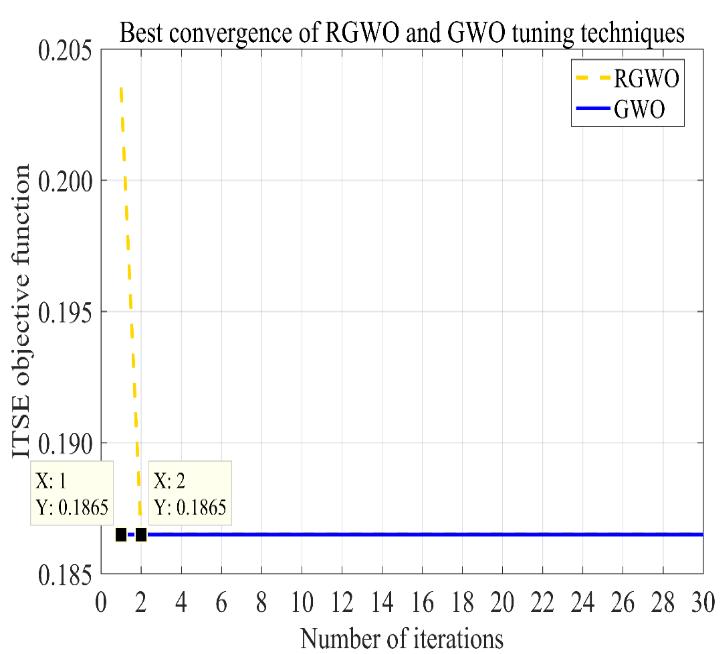
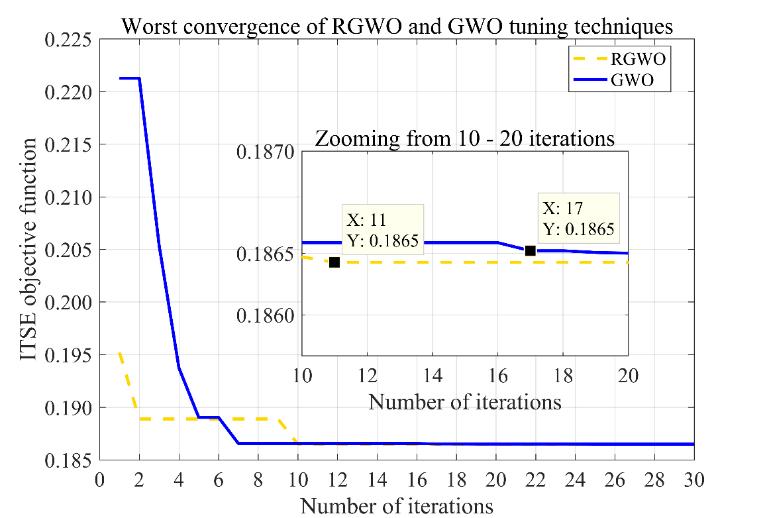
FromthebestcaseinTable2,theGWOconvergedinto theglobaloptimumof1.865x10-01inthe1st iterationwhile theRGWOconvergedinthe2nd iterationasshowninFigure 4. The worst convergence result is presented in Table 2, where the GWO converged into the global optimum of 1.865x10-01 inthe17thiterationwhiletheRGWOconverged inthe11th iteration.Theworst-caseconvergencecurvesof thetwotuningtechniquesareshowninFigure5.The
convergence results show that the GWO convergence speed is enhanced by modifying the GWO parameter for updatingthepositionsofthewolvesfromthebestpositions vectorsofα,βandδ andwolves.ConsideringTable2,the RGWOcomputedtheleastmeanvaluesof KP gainequalto 4.446whiletheGWOcomputedahigheraveragevalueofKP equalto5.00.
TheRGWOcomputedtheleastaveragevaluesofKPgains equalto11.884whiletheGWOcalculatedthehigheraverage valueKI equalto12.547.
Table- 2: TuningresultsforRGWOandGWOalgorithms
These tuning results obtained from RGWO and GWO indicate that replacing the numerator of best positions vectorsof and wolvesofEquation(7)oftheGWOwith avectorpresentedinEquation(27)toformtheRGWOhas increasedtheconvergencespeedofthe GWOandreduced thevaluesofthePItunedgainsobtainedfromtheGWO.

3. CONCLUSIONS
TheoptimaltuningofthePIcontrollerinpitchcontrolofthe windturbineusingGWOandRGWOisconducted,wherethe RGWO provided better-tuned gains and showed faster convergencethanGWO.Both GWOandRGWOdidnottrap intoalocaloptimumduringthetuningofthePIcontroller. Therefore, it can be concluded that the RGWO tuning techniqueisbetterthanGWO forthePIcontrollertuningin the pitch control of the Wind Turbine. The contributionof thisstudyisthemodificationofupdatingparameterofthe GWO parameter, which models the updating of wolves' positionsfromthebestpositionsofα,βandδwolves,and thisenhancedtheaverageconvergencespeedoftheGWO. Furthermore, the modification of the GWO updating parameterprovidedbetter-tunedgainsforthePIcontroller inthepitchcontroloftheWindTurbine.Thefastersettling timeinpitchcontroloftheWindTurbineprovidedbythe modifiedGWOcanreducethestressinthepitchcontrolof theWindTurbinecomparedtoGWO.
ACKNOWLEDGEMENT
The author wishes to acknowledge the support from the Universiti Teknologi Malaysia online literature and TETFundNigeriaforsponsoringtheconductofthisstudy.
REFERENCES
[1] S.Mirjalili,S.M.Mirjalili,andA.W.O.Lewis,“GreyWolf Optimizer,” Adv. Eng. Softw., vol. 69, pp. 46–61, 2014, doi:10.1016/j.advengsoft.2013.12.007.
[2] S.K.Verma,S.Yadav,andS.K.Nagar,“Optimizationof Fractional Order PID Controller Using Grey Wolf Optimizer,” J. Control. Autom. Electr. Syst.,vol.28,no.3, pp.314–322,2017,doi:10.1007/s40313-017-0305-3.
[3] J.LuoandZ.Liu,“Novelgreywolfoptimizationbasedon modified differential evolution for numerical function
optimization,” Appl. Intell.,vol.50,no.2, pp. 468–486, 2020,doi:10.1007/s10489-019-01521-5.

[4] F.B.Ozsoydan,“Effectsofdominantwolvesingreywolf optimizationalgorithm,” Appl. Soft Comput. J.,vol.83,p. 105658,2019,doi:10.1016/j.asoc.2019.105658.
[5] N.Mittal,U.Singh,andB.S.Sohi,“ModifiedGrey Wolf Optimizer for Global Engineering Optimization,” Appl. Comput. Intell. Soft Comput.,vol.2016,pp.1–16,2016, doi:10.1155/2016/7950348.
[6] S.Padhy,S.Panda,andS.Mahapatra,“AmodifiedGWO technique based cascade PI-PD controller for AGC of powersystemsinpresenceofPluginElectricVehicles,” Eng. Sci. Technol. an Int. J.,vol.20,no.2, pp. 427–442, 2017,doi:10.1016/j.jestch.2017.03.004.
[7] A. A. Heidari and P. Pahlavani, “An efficient modified grey wolf optimizer with Lévy flight for optimization tasks,” Appl. Soft Comput. J.,vol.60,pp.115–134,2017, doi:10.1016/j.asoc.2017.06.044.
[8] S. Yadav, S. K. Verma, and S. K. Nagar, “Optimized PID ControllerforMagneticlevitationSystem,”in 4th IFAC Conference on Advances in Control and Optimization of Dynamical Systems, 2016, vol. 49, no. 1, pp. 778–782, doi:10.1016/j.ifacol.2016.03.151.
[9] T.Han,X.Wang,Y.Liang,Z.Wei,andY.Cai,“Anovelgrey Wolf optimizer with random walk strategies for constrained engineering design,” 2018 ACM Int. Conf. Proceeding Ser., pp. 1–6, 2018, doi: 10.1145/3148453.3306270.
[10] Z. Civelek, E. Çam, M. Lüy, and H. Mamur, “Proportional-integral-derivative parameter optimisationofbladepitchcontrollerinwindturbines by a new intelligent genetic algorithm,” IET Renew. Power Gener.,vol.10,no.8,pp.1220–1228,2016,doi: 10.1049/iet-rpg.2016.0029.
[11] T. L. Van, T. H. Nguyen, D. Lee, and S. Member, “AdvancedPitchAngleControlBasedonFuzzyLogicfor Variable-Speed Wind Turbine Systems,” IEEE Trans. ENERGY Convers.,vol.30,no.2,pp.578–587,2015,doi: 10.1109/TEC.2014.2379293.
[12] D. Pathak and P. Gaur, “A fractional order fuzzyproportional-integral-derivative based pitch angle controller for a direct-drive wind energy system,” Comput. Electr. Eng., vol. 78, pp. 420–436, 2019, doi: https://doi.org/10.1016/j.compeleceng.2019.07.021.
[13] G.B.GenovJ,VenkovG,“Modellingandcontrolofa wind turbine,” Inf. Technol. Control, no. July, pp. 1–9, 2012.
[14] M. K. Dhar, M. Thasfiquzzaman, R. K. Dhar, M. T. Ahmed,andA.AlMohsin,“Studyonpitchanglecontrol ofavariablespeedwindturbineusingdifferentcontrol strategies,” in 2017 IEEE International Conference on Power, Control, Signals and InstrumentationEngineering (ICPCSI), 2017, pp. 285–290, doi: 10.1109/ICPCSI.2017.8392258.
[15] M.Q.Duong,F.Grimaccia,S.Leva,M.Mussetta,and E. Ogliari, “Pitch angle control using hybrid controller foralloperatingregionsofSCIGwindturbinesystem,” Renew. Energy, vol. 70, pp. 197–203, 2014, doi: 10.1016/j.renene.2014.03.072.
[16] C.Jauch,S.M.Islam,P.Sørensen,andB.BakJensen, “Design of a wind turbine pitch angle controller for powersystemstabilisation,” Renew. Energy,vol.32,no. 14, pp. 2334–2349, 2007, doi: 10.1016/j.renene.2006.12.009.
[17] S. Soued, M. A. Ebrahim, H. S. Ramadan, and M. Becherif,“Optimalbladepitchcontrolforenhancingthe dynamic performance of wind power plants via metaheuristicoptimisers,” IET Electr. Power Appl.,vol. 11, no. 8, pp. 1432–1440, 2017, doi: 10.1049/ietepa.2017.0214.

[18] A.MadadiandM.M.Motlagh,“OptimalControlofDC motor using Grey Wolf Optimizer Algorithm,” Tech. J. Eng. Appl. Sci.,vol.4,pp.373–379,2014.

[19] P.Niu,S.Niu,N.liu,andL.Chang,“Thedefectofthe Grey Wolf optimization algorithm and its verification method,” Knowledge-Based Syst., vol. 171, pp. 37–43, 2019,doi:10.1016/j.knosys.2019.01.018.
BIOGRAPHY
Dr AliyuHamzaSuleisaPrincipalLecturer Depart.ofElect.Eng'gatHUKPolytechnic Katsina. He obtained a Ph.D. in Electrical Engineering in 2021 from UTM, Malaysia. HisresearchinterestsincludeOptimization of Power System using Metaheuristic Optimizers, Integration of RES in Power System, Power System Stability and Control
APPENDIX
Table-3: SCIG Wind Turbine, Grid, Transformer and Line parameters[13] SCIG
