Development of an Explainable Model for a Gluconic Acid Bioreactor and Profit Maximization through G

Development of an Explainable Model for a Gluconic Acid Bioreactor and Profit Maximization through Grey Wolf Optimizer Trained Artificial Neural Network Technique

Abstract - The current study focuses on building a model of a laboratory scale bioreactor using a grey wolf optimizer trained ANN approach, then optimizing it for profit maximization. The glucose to gluconic acid bioprocess was employed as a case study. The fermenter is a multiphase enzymatic bioreactor and developing a viable first principlebased model is difficult due to its complexity; on the other hand, data-driven models lack explanability.Asaresult,inthis study, a general methodology was developed in which a datadriven technique such as the grey wolf optimizer trained ANN technique was used as a modelling tool, and the model was then post-processed to increase themodel'sexplainability.The model was chosen for its ability to accurately describe the underlying physics of the system. It was subjected to optimization after the establishment of an acceptable model. The goal of this study was to maximize gluconic acid yield, which has a substantial impact on the process' profitability. Using an evolutionary algorithm on the created model, an ideal solution was determined.

Key Words: Grey wolf optimizer trained ANN technique; Bioprocess;Modelling;Optimization;Geneticalgorithm

1.INTRODUCTION

The business environment has altered drastically in the previous decade as a result of severe worldwide competition. Because of globalisation, chemical process industriesareseeingtheirprofitmarginserodeasaresultof moreharshcompetitioninavolatilemarket.Theonlywayto properly mitigate these challenges is to improve process efficiencythroughyieldmaximisationthroughtechnological innovation. Chemical companies all around the world are seekingfornewandinnovativewaystosavecostsandboost revenues. The application of artificial intelligence-based techniques to extract value from huge amounts of experimental data through data mining and knowledge discovery is one of the most intriguing creative tactics to investigate.

Chemicalbioreactorsarecatchingtheinterestofscientists who are looking for new methods to make money. The reactoristheonlymajorpieceofmachinerythataddsreal valuetorawmaterialsbyturningthemintofinishedgoods. In this aspect, reactor optimization has a tremendous potentialimpactonoverallprofitability[1].Asafirststepin

optimizing the bioreactor, modelling complex systems of chemical processes is critical. In biochemical reactions, complex reaction kinetics and thermodynamics were involved. Building a credible phenomenological model for bioreactors is a time-consuming and difficult task that requires a detailed grasp of heterogeneous catalytic behavioursuchasmassdiffusionandcatalystdeactivation, among other things. Furthermore, in laboratories, various parameterssuchasagitationspeed,temperature,negative influence of toxins contained in incoming gas, diffusional coefficients, and others affect reaction rate, yield, and selectivity,theprocessesofwhichareunknown.Asaresult, the reactor's optimization is hampered by a lack of understandingofchemicalreactiondynamics.Forsafetyand dependabilityconcerns,mostchemicalbioreactorsremaina black box, and scientists do not tamper with them. This causes bioreactors to operate inefficiently, which has a considerableinfluenceontheprofitability.Asaresult,inthe chemical sector, reactors are viewed as an unknown territory. A minor increase in catalyst selectivity and reactionyield,ontheotherhand,hasamajorimpactonraw materialconsumptionandoverallprofitabilityinlarge-scale operations.[1].

To derive the kinetic equation of a given biochemical reaction, laboratory scale kinetic analysis is typically performed in a very ideal and controlled context. The applicability of such an approach for kinetic modelling of bioreactorsisquestionableduetothepresenceofpoisons and inert in input gases, and the varying heat and mass transferenvironment.Furthermore,chemicalengineersare unwilling to commit adequate time and effort to a full examinationofthesecomplexreactionmechanismsdueto the restricted market window for chemical goods. As a result,analternativestraightforwardmethodistodevelop approximatedreactormodelsforthesecomplicatedreaction systems using a data-driven effective computational strategy,whichcanthenbeusedtooptimizethereactorand increaseprofit.

The key challenge is figuring out how to leverage this plethora of data to produce more money, because most chemical laboratories collect and store vast volumes of reactorinputandoutputoperationaldata.Dataisthenew oil,anddata-drivenmodellingtoolssuchasartificialneural networks(ANN)andsupportvectormachines(SVM)arethe

newICenginesofourday.Inthelastdecade,ANNandSVR have become very popular black box modelling methodologies,withanumberofapplicationsdevelopedfor biochemical reactors. Engineers, on the other hand, reject ANN and SVM models because they are difficult to understandandprovideablackboxmodel.TheANNmodel offers no insight into the underlying physics of chemical reactors.

Despiteitshighpredictioncapacity,themodelsuffersfrom explainability limits because it produces a black box type equation consisting of a complex sigmoidal function with several tuning elements known as weights and biases. To acquirebetterunderstandingandprofit,processengineers preferintelligibleequationsindifferential/algebraicform thatrelateoutputvariablestoinputfeatures.Aclosedform equation that can describe the effect of key process parametersontheoutputvariableispreferredinthecreated model.SVMandANNbothhavethedifficultyofproviding closed form explainable equations that are portable and simpletoimplementinaDCSsystem.Gaininginsightsand obtaining a closed form explainable model equation is crucialforengineerstoacceptthemodel'suseinreallife

Despite the ANN's outstanding prediction skills, there are fewusesofthistechnologyinchemicalreactionengineering workinbiochemicalreactors.Anattemptwasmadeinthis work to use ANN modelling on a gluconic acid bioreactor. OneofthemainobjectivesofthisstudyistoconverttheANN modelintoanexplainableclosedformequation,whichwill givecrucialinformationaboutthereactor'sphenomenology. ThesecondpurposeofthisprojectistotraintheANNmodel usingfreshlyfoundnature-inspiredgreywolfoptimization methodologies. Learning is a vital part of every neural network,andithaspiquedtheinterestofmanyresearchers. Inmostapplications,thetraditional[7]orupgraded[8–10] Back-Propagation (BP) algorithm is employed to train feedforward neural networks(FNNs).TheBP method isa gradient-basedalgorithmwithsomeflaws,includingdelayed convergence [11] and a proclivity to stay stuck in local minima[12].DuringthelearningprocessofFNNs,thegoalis toidentifythebestcombinationofconnectionweightsand biases to achieve the least amount of error. FNNs, on the otherhand,frequentlyconvergeonpointsthatarethebest answer locally but not worldwide. In other words, rather than the global minimum, learning methods lead FNNs to local minima. According to [13], the BP algorithm's convergenceisstronglydependentontheweights,biases, andparameters'initialvalues.Learningrateandmomentum aretwoofthesecharacteristics.Apopularapproachinthe literatureistoenhancetheproblemsofBP-basedlearning algorithmsbyusinguniqueheuristicoptimizationmethods orevolutionaryalgorithms.

Someoftheheuristicoptimizationapproachesusedtotrain FNNs include Simulated Annealing (SA) [13,14], Genetic Algorithms(GAs)[15],ParticleSwarmOptimization(PSO)

algorithms[16–20],MagneticOptimizationAlgorithm(MOA) [21],andDifferentialEvolution(DE)[22].Somealgorithms, suchasSAandGA,canreducethechance oflocal minima trapping, but they still have poor convergence rates, accordingto[11].

Despite the widespread usage of meta-heuristics in ANN learning, none of them has done well in all applications. Existingmetaheuristicsalsohaveanumberofflaws[23-27], suchasslowconvergencespeed,trappinginlocalminima, long computational time, tuning many parameters, and a difficult encoding scheme. As a result, it appears that boostingtheefficiencyofANNlearninginvariousdomains requireseitherimprovingtheperformanceofexistingmetaheuristics or proposing new ones. [18] presented GWO, a new stochastic and metaheuristic optimization technique. The efficacy of the GWO approach for training FNNs is studiedinthiswork.

Because of its financial importance in global markets, the current study chose to model a gluconic acid bioreactor. Gluconic acid is used as the metal supplement of calcium, iron,etc.inpharmaceuticalsandasanacidulentinthefood industry. It also finds applications as a biodegradable chelatingagent,filler,metalcleaner,dyestabilizer,andinthe textile industry for removing instructions. A reliable first principle-basedmodelisrarelyaccessibleintheliterature duetoalackofunderstandingandcomplexityofmultiphase enzymaticreactionsoccurringingluconicacidbioreactors. Datadrivenmodellingisapotentialalternativestrategydue tothevastamountofbioreactoroperatingparameterdata available after multiple runs. The current project aims to make use of a huge amount of process data to create a frameworkforconvertingthedata'sinformationintoprofit.

The study's next goal is to use the developed model to increasethegluconicacidfactory'sprofit.Thisisperformed by optimizing the input process parameters utilising a model-based, nature-inspired metaheuristic optimization methodinordertoenhancegluconicacidyield(i.e.,reactor performance).TheGAisusedtoimprovetheinputspaceof thebioreactor’sANNmodelinordertogiveparetooptimum solutions that achieve the objective in the most efficient mannerpossible.

2. Case study of gluconic acid bioreactor

2.1. Background

Because of the lack of understanding and complexity of multiphase catalytic processes in lab scale batch reactors, trustworthyfirstprinciple-basedmodelsarehardtocome by.Datadrivenmodellingisafeasiblealternativestrategy duetothevastamountofreactoroperatingparameterdata availablefrombioreactors.Thecurrentprojectaimstomake useofahugeamountofprocessdatatocreateaframework forconvertingthedata'sinformationintoprofit.

2.2. Reactions:

Commercially,gluconicacidisproducedprimarilyusing two biological methods,but moreexpensivechemical and electrochemicalwaysarealsoavailable.Themostprevalent biochemical approaches are freecell fermentation and immobilisedenzyme-basedglucosebioconversion(glucose oxidase,GOD,ofAspergillusnigerandGluconobacter).The GOD converts glucose to glucono-d-lactone, which is then hydrolyzedbylactonasetogluconicacid.Producinggluconic acid with immobilised enzymes is a costly and timeconsumingtechniqueduetoobstaclesintheimmobilisation andseparationphases;extradifficultiesdevelopasaresult of denaturization of the enzymes. During free-cell fermentation,myceliaareexposedtoavarietyofmassand heat-transfer stresses. Mechanical agitation aids in the removaloftheserestrictions,butitcreatesaturbulentflow thatcanresultincelldisintegration,cellfractureorsurface erosion, and pellet breaking. As a result, there may be a suddenorgradualdeclineincellularactivity.Ontheother hand,fermentationofgluconicacidbycellsimmobilisedona support matrix under submerged conditions is a costeffectiveandefficientmethod.

Gluconic Acid Yield= (Moles of gluconic acid produced)/(Moles of glucose consumed)(1)

2.3. Process flow diagram

A new batch fermentation procedure for producing gluconicacidfromglucosehasrecentlybeendevised,withA. niger immobilised on a cellulosic fabric support matrix generatinghigheryields.Theenhancedoverallproductivity ofthistechniqueismostlyduetotheincreasedinteraction between dissolved oxygen and the fungal mycelia. To optimisetheaforementionedreaction,acontinuoussubstrate dripping mechanism (see Figure 1) is used instead of the mechanical agitation used in free-cell fermentation. As a result,thebioreactor'syielddeterminesthetotalprofitability.

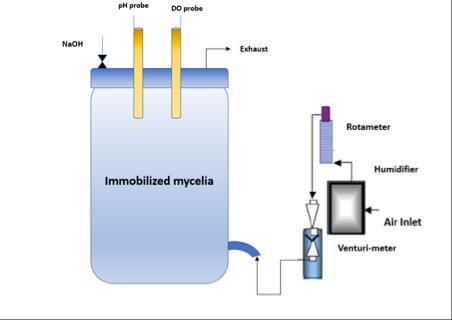
2.4. Production Objectives

Thepurposeofthisresearchistodevelopamathematical model of the new glucose to gluconic acid batch fermentation process and to discover the best process conditions for higher gluconic acid yield. The fermenter model was built using experimental data that took into account the impacts of substrate (glucose), biomass, and dissolved oxygen levels. Figure 1 depicts the complex reactionandmasstransferpathwaysinvolvedintheglucose togluconicacidbioconversionusingA.nigerimmobilisedon cellulosemicrofibrils.Becausethephysicochemicalevents thatdrivebioconversion,aswellasthekineticandtransport mechanismsthatfollowthem,arepoorlyunderstood.

3. Background materials

Thispartdiscussesthefundamentalbackgroundmaterials required for a complete understanding of the proposed method. The Multi-layer perceptron (MLP) as a Feedforwardneuralnetwork(FNN)isintroducedfirst,followed by GWO approaches, which are then compared to the suggested technique for MLP learning in bioreactors modelling.MLPnetworkisfollowedbyabriefdiscussionof thehybridANNandGWOtrainingmethod.

Thefeed-forwardneuralnetwork(FFNN)isoneofthemost common ANNs and receives a lot of academic attention because of its ability to map any function to an unlimited degree of precision. The multi-layer perceptron has been employedinavarietyofsectors,includingfinance,medicine, engineering,geology,physics,andbiology.Nonlinearprocess modelling, fault diagnostics, and process control are all commonapplicationsinthefieldofchemicalengineering.

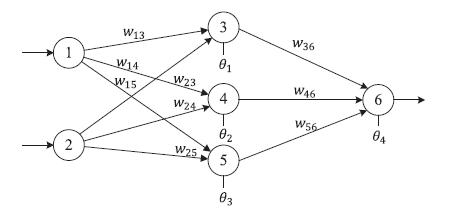
As shown in Figure 2, MLP contains one input layer that receivesexternalinputs,oneormorehiddenlayers,andone output layer that displays the results. All levels, with the exception of the input layer, are made up of processing nodes and activation functions. The input layer provides data, and the network nodes perform calculations in successivelayersuntileachoutputnodereceivesanoutput value.

3.1. Training of ANN by GWO

There are three techniques to train FNNs with a heuristic algorithmingeneral.Theidealmixofweightsandbiasesfor aFNNwiththeleastamountoferrorisfirstdiscoveredusing heuristictechniques.Second,inordertofindtheappropriate structure for a FNN in a specific situation, heuristic approachesareapplied.Finally,anevolutionaryalgorithm can be used to tune the parameters of a gradient-based learningsystem,suchasthelearningrateandmomentum.

In the first scenario, the structure is fixed before training FNNs.Thegoalofatrainingmethodistofindagoodvalue forallconnectionweightsandbiasesinordertolowerthe FNNs'totalerror.Inthesecondinstance,theFNNstructures are different. A training technique is applied to a FNN to determinetherightstructureforagivenproblem.Change the structure of the FNN by manipulating the connections between neurons, the number of hidden layers, and the numberofhiddennodesineachlayer.

ThefirsttechniqueinthisstudyisusedtoapplyGWOtoa FNN;theseoperationsarereferredtoashybridFNN-GWO. TheFNN'sstructureisfixed,andtheGWOmethodchoosesa setofweightsandbiasesthatgivestheFNNtheleastamount of error. In order to design FNN-GWO, the following fundamentalfeaturesmustbedefined.InFNN-GWO,builda fitness function based on the FNN's mistake before evaluatingagents'fitness.Second,anencodingstrategyfor theFNN-GWOagentsshouldbedevisedtoencodetheFNN's weightsandbiases.Theseelementsaredescribedinfurther depthbelow.

3.1.1. Fitness function

Thefitnessfunctionusedinthisarticle[10]hasthefollowing formula:

InFigure2,whichhastwolayers,thenumberofinputnodes isequalton,thenumberofhiddennodesisequaltoh,and thenumberofoutputnodesisequaltom.(oneinput,one hidden,andoneoutputlayer).Attheendofeachlearning period, the output of each hidden node is calculated as follows: ,j= 1,2,…,h (2)

In ,nisthenumberoftheinputnodes, wij is the connection weight from the ith node in the input layer to the jth node in the hidden layer, Ɵj is the bias (threshold)ofthejth hiddennode,andxiistheith input.

After calculating outputs of the hidden nodes, the final outputcanbedefinedasfollows:

, k = 1,2, …, m, (3)

wherewkjistheconnectionweightfromthejth hiddennode tothekthoutputnodeandƟk isthebias(threshold)ofthe kth outputnode.

Finally,thelearningerrorE(fitnessfunction)iscalculatedas follows:

whereqisthenumberoftrainingsamples, isthedesired outputoftheith inputunitwhenthekth trainingsampleis used,and istheactualoutputoftheith inputunitwhen the kth training sample is used. Therefore, the fitness functionoftheithtrainingsamplecanbe definedasfollows:

3.1.2

Encoding strategy

FollowingthespecificationoftheFNN-GWOfitnessfunction, the next step is to select an encoding technique for each FNN-GWO agent to encode the FNN's weights and biases. There are three approaches to encode and express the weightsandbiasesofFNNsforeachagentinevolutionary algorithms, according to [10]. These are the methods of vector,matrix,andbinaryencoding.Eachagentisencoded asavectorinvectorencoding.Duringtraining,eachagent reflects all of the FNN's weights and biases. Each agent is encoded as a matrix in matrix encoding. Because we're interested in training FNNs, we've employed the matrix encoding technique in this piece. An example of this encoding strategy for the FNN of Figure 2 is provided as follows:

whereW1isthehiddenlayerweightmatrix,B1isthehidden layerbiasmatrix,W2istheoutputlayerweightmatrix, is thetransposeofW2,andB2 isthehiddenlayerbiasmatrix.

3.2. Grey Wolf Optimization (GWO): at a glance GWO, a new stochastic and metaheuristic optimization technique, was introduced by [28]. GWO's purpose is to mimicthecooperativehuntingbehaviourofgreywolvesin thewild.Thegreywolfpack'shierarchicalorganisationand predation behaviour are promoted by this bionic optimization approach, in which the wolves take prey by surrounding,haunting,andattackingitunderthecommand ofthetopgreywolf[31].Thetopthreegreywolveswerethe targetofthislarge-scalesearchmethodology,buttherewas nowaytoeliminatethem.Theoptimizationtechniquediffers fromothersintermsofmodelling.AsshowninFigure3,it producesastricthierarchicalpyramid.

following equations are proposed for mathematically modelling.

Thetypicalsizeofagroupis5-12persons.Thelayer,which consistsofamaleandfemaleleader,isthemostpowerful andcapablememberoftheteamwhenitcomestomaking decisionsonpredationandotheractivities.Thesecondand thirdlayersofthehierarchy,respectively,areincharge of aidinggrouporganisationsintheirbehaviour.Thebottomof thepyramid,oftenknownas,ishometothemajorityofthe world's population. They are largely responsible for satisfying the entire pack by maintaining the dominance hierarchy,regulatingthepopulation'sinternalconnections, andcaringfortheyoung[28].GWOmathematicalmodelling:

ThemainkeypointoftheGWOmodelisthesocialhierarchy, encircling,hunting,attackingandsearchingprey.

A. Socialhierarchy

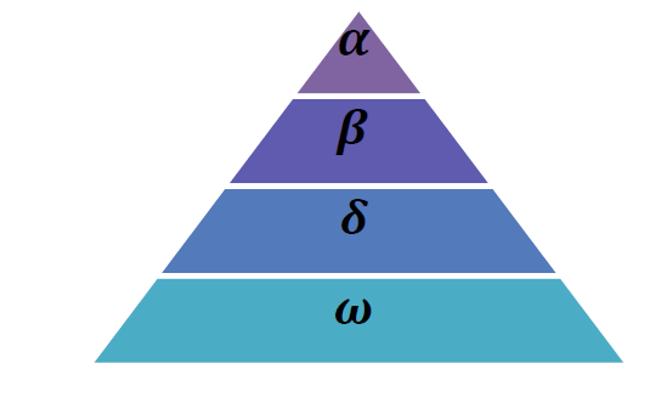
Inthe model of GWO,α isconsideredas fittestsolution.β and δ are considered as second and third best solution, respectively.Therestofthesolutionsareassumedtobeω.

B. Encircling

Atfirst,thelocationofthepreyisdeterminedandduringthe hunting process grey wolves encircled the prey. The

Where is the number of current iterations, is the position vector of one grey wolf, is the next positionvectoritarrives, isthepositionvectorofthe prey, and arecoefficientvectorswhichareevaluatedas follows:

and arerandomvectorsin[0,1],aisdecreasingvalue duringthe iterationin[0,2], typically (Iis themaximumnumberofiterations).

Inthisconcept,greywolvesmovearoundthebestsolution inhyper-cubes withinan n dimensional spaceand able to detectthepositionofthepreyandencircleit.

C. Hunting

Greywolveshavetheabilitytohuntpreywiththeguidance of alpha after encircling the prey. The beta and delta also take part in the hunting procedure on occasion. The first three best solutions in the mathematical stimulation of huntingbehaviourupdatethepositionofothersearchagents (including the omegas). In this approach, the following equationsareproposed.

D. Attackingprey(exploitation)

Grey wolves complete the hunting phase and ready to capture the prey. For the purpose of mathematically modelling,thevalueof graduallydecrease.Therefore,the fluctuationrateof isalsodecreasedby . where a is decremented from 2 to 0 over the course of iterations.Whentherandomvaluesof ,thenext positionofsearchagentcanbeinanypositionbetweenits current position and the position of the prey. When ,the greywolveswoulddivergefrom the prey to achieveglobalsearchandwhen ,thegreywolves wouldconvergetowardsthepreyandcompleteit.

E. Searchingprey(exploration)

GWOalgorithmusesanefficientexplorationmethodologyby allowing its search agents to update their position on the basisofalpha,beta,deltaandattackstowardstheprey.This mechanismcreatesagooddiversityintheproblemsearch space.Greywolvesarestayawayfromeachotherforglobal searchofpreyandclosetoeachotherforattackingtheprey. For ,valuesbetween1and-1aretaken. vectorisalso favouredtheexplorationtechniqueandrandomvalues are used. After generating the random population, alpha, betaanddeltadeterminedthepositionofthebestprey.For selectionof explorationand exploitation,thevalue of is decreasedfrom2to0respectively.

The GWO algorithm terminates when the criterion is satisfied.Thismetaheuristicapproachisappliedinvarious real-world problems because of its efficient and simple performanceabilitybytuningthefewestoperators[28-32].

3.3. Hybrid learning of GWO and FNN network

Inthissection,GWOisusedtolearnFNN.Ahybridlearning of GWO and FNN networks (GWO-FNN) is utilised to increase the network's accuracy. The algorithm will simultaneously determine the set of weights and their relatedaccuracybytrainingthenetwork.TheFNNnetwork's network weights and biases can be expressed as a Ddimensional vector. The vector for FNN is defined by Equation 16. To optimize the FNN weights using GWO methods,eachparticle'sdimensionisregardedasavectorD.

D=(Input×Hidden)+(Hidden× Output)+Hidden bias + Outputbias, (16)

whereInput,HiddenandOutputarereferredthenumberof inputs, hidden and output neurons of FNN network respectively. Thenumberofbiasesinthehiddenandoutput layers is also known as Hidden bias and Output bias. A datasetiscollected,normalized,andreadtobegintheGWOFNN. Following that, the appropriate number of inputs, output, and hidden neurons are specified to establish the particle dimension as Equation (5). The population is

initialized,andthetrainingerrorisdeterminedasafitness function following FNN training. Every particle (wolf) modifies its velocity and position based on training error. ThenewplacesrepresenttheFNNnetwork'snewweights, which are supposed to minimize the fitness function. The fitnessfunctioniscomputedbasedontestseterror.These stepswillgoonuntilmeetingstopconditions.

4. MATHEMATICAL MODELLING OF BIOPROCESS

4.1. Selection of input and output variables for modelling

Because reactor yield has such a large impact on overall profitability, it is kept as an output variable. All reactor operational factors that could affect yield are stored as a "wish list" of input variables. Initially, all bioreactor experimental data was acquired. Following that, all of the input factors that could affect the output variable were recorded after speaking with a technical specialist. After that, a cross-correlation analysis was carried out. This methodwasusedtodeterminethecorrelationcoefficientsof eachinputvariablewiththeoutputvariable,aswellasthe interinputcross-correlationcoefficients.

The following criteria are used to shortlist the input variables.

(i) Foraparticularinputvariable,thereshouldbehigh cross-correlation coefficient with output variable.

(ii) Thevaluesofcross-correlationcoefficientsofinter inputvariablesshouldbelow.

(iii)Theinputsetofvariableswerekeptasminimumas possibletoavoidcomplexityofthemodel. Based on the above criteria 3 input variables are finally shortlistedandtabulatedinTable1.

Variables used in modeling Data Range

Input Variables

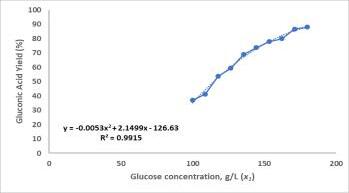
Glucoseconcentration,g/L(x1) 100.0–180.0

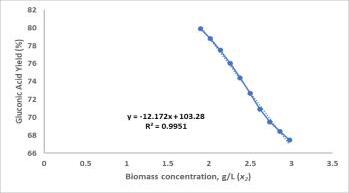
Biomassconcentration,g/L(x2) 1.00–3.00

Dissolved oxygen concentration, mg/L (x3) 10.0–60.0

Output Variables

GluconicAcidYield,%(Y1) 5.9–94.58

4.2. Data collection, Data cleaning and removal of outliers

TheGWO-FNNbasedmodelfortheglucosetogluconicacid bioprocess was created using experimental input-output data from the fermenter. In this study, the gluconic acidproducingstrainAspergillusnigerNCIM545wasemployed. The spore germination media, growth medium, and cellulosic fibre support have all been well reported previously.

The quality of data used to build a data-driven model is widelyacceptedasdeterminingthemodel'squality.Because noisyanderroneousdatacanhaveamajorimpactonmodel performance, data quality is an important consideration when employing data driven modelling. Due to the high number of process data, this research developed an automateddatacleaningtechniquethateliminatestheneed for human intervention. In this work, the data was preprocessedusingmultivariatePrincipalComponentAnalysis (PCA). An automated MATLAB-based system was built to buildamultivariatestatisticalvectorcalledt-squaredfrom the operating dataset. The corresponding rows in the tsquared vector with values over the 95th percentile was thereforeconsideredoutliersandwereeliminatedfromthe dataset.

4.3. Modelling through FNN-GWO algorithm

AnANN-basedmodelwasbuiltusingthecleanseddata.The dataset,whichincludedeightinputvariablesandtwooutput variables(Table1),wasdividedintoatrainingset(80%of the total data) and a test set (the remaining 20%). (20 percentofthetotaldata).Thetrainingdatasetwasusedto buildthemodelbymaximisingthefitnessvalue,andthetest data set was used to cross-validate the result. Cross-main validation's purpose is to improve the model's generalizability.

TheFNN-GWO-basedmodelwasdevelopedusingMATLAB 2019acode.Themean-squarederror(MSE)betweenactual andprojectedoutputswasemployedasthefitnessfunction inthisstudy,andtheprogrammewasruninsuchawaythat theMSEvaluewasminimized.Duetothestochasticnature of the ANN, the software was run 100 times to create the model.

4.4. Optimization through Genetic Algorithm

Themodelisthenutilizedtooptimizethebioreactorprocess parameters once a trustworthy and accurate bioreactor model has been built. The goal is to find the best process conditions for maximal bioreactor profitability. In other words,theoptimizationalgorithmshouldaimforthehighest possiblereactoryield.

Amulti-objectivegeneticalgorithmisutilisedinthisstudyto establishabalancebetweentwoopposinggoals.Thegenetic

algorithm(GA)hasshowntobeapowerfuloptimizationtool that has been applied to a wide range of technical and medicalapplications.

ForimplementationofGAalgorithm,anobjectivefunction wasdevelopedwhichisasfollows(Equation17):

F1(x) = 1/Y1(x) (17)

where Y1(x) isthe function ofthemodel corresponding to gluconic acid yield. Therefore, in GA F1(x) has to be minimizedinordertomaximizetheyieldofthebioprocess.

5. Results and discussions

5.1. Performance of FNN-GWO model

The major purpose of this study is to create an accurate, simple, portable, and easy-to-understand closed model equationforabioreactor.

ThevaluesofANNparametersrequiredformodellingwere determinedusingatrial-and-errorapproachandaliterature review. In the current work, the number of nodes in the hidden layer fluctuates consistently from 5 to 25, and the FNNGWOapproachisusedtofindtheappropriateweights andbiasthatproducethelowestMSEbetweenactualand anticipatedoutputeachtime.

Shortlisting the models: Tochoose a valid model froma pooloflikelycandidatesorrepresentativemodelequations with varying degrees of complexity and accuracy, the followingcriteriawereused:

(i) Simplicity:Themodelshouldbeasstraightforward aspossible.Modelcomplexitywasdetermined bythenumberofnodesinthehiddenlayer.

(ii) Predictionaccuracy:Thegapbetweenexpectedand actualyield.

(iii)Thefundamentalphysicsoftheprocessshouldbe captured in the model equation. To put it anotherway,modelequationsshouldincludea physical understanding of the system under investigation rather than just a prediction relationship.Thisisanimportantconsideration forbuildingrealisticreactormodels.

explainable to engineers. Equation is simple and contains termsorparametricco-efficientwhichthrowlightsrelative importance of each parameter on the overall yield if they deviatefromthisbasevalue.Also,itindicateswhetherthe effectofeachparameterislinearornon-linear.

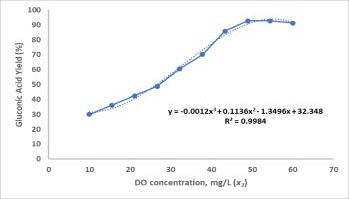
Equation 18 is then used to predict yield of experimental dataandpredicted,andactualyieldiscompared.Prediction erroris0.42%andR2 is0.99.Thislowvalueofprediction errorandhighvalueofR2 signifiesthatdevelopedequation (equation18)ishighlyaccurateandreliable.

time. Due to unavailability of an explainable model, since scientists have no idea about optimal solution, experimentalists try to optimize the process heuristically basedontheirexperienceandknowledge. Theonlyaction scientistmustdoistoruntheGAwithproperboundinrealtime, and GA will provide a set of optimum operating conditionsthatthescientistneedstosetintheexperiment.

6. Conclusion

Fromtheexistingoperatingdata,thisstudyusesArtificial Neural Networking to construct an accurate model of a gluconic acid bioreactor. An ANN creates a closed model equation that is portable and may be used in a control system. The true value of this research is that it has produced an explainable model equation that is very accurate and provides insights into the process. The produced model equations are based on the underlying physicsoftheprocessandareinlinewiththeobservations and experiences of the experimentalist. After that, the developedmodelequationsareusedtoconstructoptimum solutionthatoptimizegluconicacidyieldandthus ensure profitmaximization.

5.2. Optimization

5.2.1. Optimization through GA

Oncethereliablemodelsweresuccessfullydeveloped,the models were subjected to optimization. Purpose of optimizationistofindtheoptimumvalueofrectoroperating parameterstoachievemaximumgluconicacidyield.Oneof thecriticaltasksforoptimizationofanyprocessisfixingof searchspaceatwhichtheoptimalprocessconditionsareto befoundout.Therefore,beforerunningtheoptimizationa lowerboundandupperboundoftheprocessvariableswere fixedinconsultationwithscientists.Thelowerbounds(LB) andupper bounds(UB)consideredinthiscasehave been depictedinTable4.

References

1. Lahiri,SandipK. ProfitMaximizationTechniquesforOperatingChemical Plants.JohnWiley&Sons,2020.

2. Lakshminarayan an, S., Fujii, H., Grosman, B., Dassau, E., Lewin, D.R., 2000. New product design via analysis of historical databases. Comput. Chem. Eng. 24, 671–676. https://doi.org/10.1016/S0098-1354(00)00406-3

3. Grosman, B., Lewin, D.R., 2002. Automated nonlinear model predictivecontrolusinggeneticprogramming.Comput. Chem. Eng. 26, 631–640. https://doi.org/10.1016/S0098-1354(01)00780-3

4. Searson, D., Willis, M., Montague, G., 2007. Co-evolution of nonlinearPLSmodelcomponents.J.Chemom.21,592–603. https://doi.org/10.1002/cem.1084

With the help of GA tool in MATLAB, the optimum experimental conditions were found out which gives the gluconicacidyieldof99.59%(Table5).Themainadvantage ofsuchastudyisthatitgivestheexperimentalengineersa strategy to run the reactor in optimum condition in real-

5. Barati, R., Neyshabouri,S.A.A.S.,Ahmadi,G.,2014.Developmentof empiricalmodelswithhighaccuracyforestimationof drag coefficient of flow around a smooth sphere: An evolutionary approach. Powder Technol. 257, 11–19. https://doi.org/10.1016/j.powtec.2014.02.045

6. Floares, Alexandru G., and Irina Luludachi. "Inferring transcriptionnetworksfromdata."SpringerHandbook

ofBio-/Neuroinformatics.Springer,Berlin,Heidelberg, 2014.311-326.

7. Horne, B.G., 1993.Progressinsupervisedneuralnetworks.Signal Process.Mag.IEEE10,8–39.

8. Hagan, M.T., Menhaj, M.B., 1994. Training Feedforward Networks with the Marquardt Algorithm. IEEE Trans. Neural Networks 5, 989–993.

https://doi.org/10.1109/72.329697

9. Adeli,H.,Hung, S.L., 1994. An Adaptive Conjugate Gradient Learning Algorithm.Appl.Math.Comput.62,81–102.

10. Zhang,N.,2009. Anonlinegradient method with momentum for twolayer feedforward neural networks. Appl. Math. Comput. 212, 488–498.

https://doi.org/10.1016/j.amc.2009.02.038

11. Zhang, J.R., Zhang,J.,Lok,T.M.,Lyu,M.R.,2007.Ahybridparticle swarm optimization-back-propagation algorithm for feedforward neural network training. Appl. Math. Comput. 185, 1026–1037.

https://doi.org/10.1016/j.amc.2006.07.025

12. Gori,M.,Tesi,A., 1992. On the problem of local minima in backpropagation.IEEETrans.PatternAnal.Mach.Intell. https://doi.org/10.1109/34.107014

13. Shaw, D., Kinsner, W., 1996. Chaotic simulated annealing in multilayer feedforward networks. Can. Conf. Electr. Comput. Eng. 1, 265–269. https://doi.org/10.1109/ccece.1996.548088

14. Koh,C.S.,Hahn, S.Y.,1994.DetectionofMagneticBodyusingArtificial Neural Network with Modified Simulated Annealing. IEEE Trans. Magn. 30, 3644–3647. https://doi.org/10.1109/20.312730

15. Montana, D.J., Davis,L.,1989.TrainingFeedforwardNeuralNetworks

UsingGeneticAlgorithms.Proc.11thInt.Jt.Conf.Artif. Intell.-Vol.189,762–767.

16. Kiranyaz, S., Ince, T., Yildirim, A., Gabbouj, M., 2009. Evolutionary artificialneuralnetworksbymulti-dimensionalparticle swarmoptimization.NeuralNetworks22,1448–1462. https://doi.org/10.1016/j.neunet.2009.05.013

17. Settles, M., Rylander, B., 2002. Neural network learning using particleswarm optimizers.Adv.Inf.Sci.SoftComput. 224–226.

18.

Zhang,C.,Li,Y., Shao,H.,2000.Anewevolvedartificialneuralnetwork anditsapplication. Proc. WorldCongr. Intell.Control Autom. 2, 1065–1068. https://doi.org/10.1109/wcica.2000.863401

19. vandenBergh, F., Engelbrecht, A.P., 2000. Cooperative Learning in Neural Networks using Particle Swarm Optimizers. SouthAfricanComput.J.26,84–90.

20. Zhang,C.,Shao, H.,Li,Y.,2000.Particleswarmoptimizationforevolving artificialneuralnetwork.Proc.IEEEInt.Conf.Syst.Man Cybern. 4, 2487

2490. https://doi.org/10.1109/icsmc.2000.884366

21. Mirjalili, S., Sadiq,A.S.,2011.MagneticOptimizationAlgorithmfor training Multi Layer Perceptron. 2011 IEEE 3rd Int. Conf. Commun. Softw. Networks, ICCSN 2011 42–46. https://doi.org/10.1109/ICCSN.2011.6014845

22. Si,T.,Hazra,S., Jana,N.D.,2012.Artificialneuralnetworktrainingusing differential evolutionary Algorithm for classification. Adv. Intell. Soft Comput. 132 AISC, 769–778. https://doi.org/10.1007/978-3-642-27443-5_88

23. Leung,Y.,Gao,Y., Xu, Z. Ben, 1997. Degree of population diversity - A perspective on premature convergence in genetic algorithmsanditsMarkovchainanalysis.IEEETrans. Neural Networks 8, 1165–1176.

https://doi.org/10.1109/72.623217

24. Hrstka, O., Kučerová,A.,2004.Improvementsofrealcodedgenetic algorithmsbasedondifferentialoperatorspreventing prematureconvergence.Adv.Eng.Softw.35,237–246.

https://doi.org/10.1016/S0965-9978(03)00113-3

25. Liang, J.J., Qin, A.K.,Suganthan,P.N.,Baskar,S.,2006.Comprehensive learning particle swarm optimizer for global optimizationofmultimodalfunctions.IEEETrans.Evol. Comput. 10, 281–295. https://doi.org/10.1109/TEVC.2005.857610

26.

Gao,W.feng,Liu, S. yang, Huang, L. ling, 2012. Particle swarm optimizationwithchaoticopposition-basedpopulation initializationandstochasticsearchtechnique.Commun. Nonlinear Sci. Numer. Simul. 17, 4316–4327.

https://doi.org/10.1016/j.cnsns.2012.03.015

27. Moslemipour,G., Lee, T.S., Rilling, D., 2012. A review of intelligent approachesfordesigningdynamicandrobustlayouts in flexible manufacturing systems. Int. J. Adv. Manuf. Technol.60,11–27.https://doi.org/10.1007/s00170011-3614-x

28. Mirjalili, S., Mirjalili,S.M.,Lewis,A.,2014.GreyWolfOptimizer.Adv. Eng. Softw. 69, 46–61. https://doi.org/10.1016/j.advengsoft.2013.12.007

29. Faris,H.,Aljarah, I.,Al-Betar,M.A.,Mirjalili,S.,2018.Greywolfoptimizer: a review of recent variants and applications. Neural Comput. Appl. 30, 413–435.

https://doi.org/10.1007/s00521-017-3272-5

30. Saremi, S., Mirjalili, S.Z., Mirjalili, S.M., 2015. Evolutionary populationdynamicsandgreywolfoptimizer.Neural Comput. Appl. 26, 1257–1263. https://doi.org/10.1007/s00521-014-1806-7

31. NadimiShahraki, M.H., Taghian, S., Mirjalili, S., 2021. An improvedgreywolfoptimizerforsolvingengineering problems. Expert Syst. Appl. 166, 113917. https://doi.org/10.1016/j.eswa.2020.113917

32. Mirjalili, S., Saremi, S., Mirjalili, S.M., Coelho, L.D.S., 2016. Multiobjective grey wolf optimizer: A novel algorithm for multi-criterionoptimization.ExpertSyst.Appl.47,106–119.https://doi.org/10.1016/j.eswa.2015.10.039

33. Singh Cheema, J.J., Sankpal, N. V., Tambe, S.S., Kulkarni, B.D., 2002. Geneticprogrammingassistedstochasticoptimization strategiesforoptimizationofglucosetogluconicacid fermentation. Biotechnol. Prog. 18, 1356–1365. https://doi.org/10.1021/bp015509s

34. Pal,S.,&Lahiri, S. K. (2022). Grey wolf optimizer trained ANN technique for development of explainable model of commercialethyleneoxidereactorandmulti-objective optimizationtomaximizeprofit.

35. Pal, S., Chowdhury,S.,Hens,A.,&Lahiri,S.K.(2022).Artificial intelligence based modelling and multi-objective optimizationofvinylchloridemonomer(VCM)plantto strikeabalancebetweenprofit,energyutilizationand environmental degradation. Journal of the Indian ChemicalSociety,99(1),100287.

36.

APPENDIX:

ExperimentalDataUtilizedforBuildingGPBasedModel