Estimation of Air-Cooling Devices Run Time Via Fuzzy Logic and Adaptive Neuro-Fuzzy Inference System
Dina Husham Alatraqchi1 , Laith A. Mohammed21 PG Student, Dept. of Computer Engineering, College of Technical Engineering, Mosul, Iraq
2 Dr, Dept. of Computer Engineering, College of Technical Engineering, Mosul, Iraq ***
Abstract - Inthis paper, fuzzy logic controller andadaptive neuro-fuzzy inference system (ANFIS) methods were applied to develop a run time control system for air-cooling devices. The system uses the current temperature and door state of the room as input variables and predicts the optimum runtime for the device. For the fuzzy logic controller, three different membership functions were assessed and their performance was evaluated. The triangular membership function displayed superior performance for the current case. The ANFIS model was developed and validated via various validation parameters to ensure it has the abilityto estimate theruntime accurately. The obtained ANFIS model showed significant validation parameters for both the training and test set. Also, the ANFIS model was superior to the fuzzy logic controller in terms of determining the optimum run time. Thus, the ANFIS modeling approach can be used as an efficient and accurate method to develop systems for controlling the run time of air cooling devices.
Key Words: Fuzzy logic, ANFIS, Embedded system, Microcontroller,Fuzzycontroller.
1. INTRODUCTION
For many years, the fuzzy logic controller has been an important and popular method [1]. Due to the imprecise nature of computer-assisted control issue solutions, the fuzzy logic controller was created. Fuzzy logic controller deals with data and processes it in a manner similar to human thinking [2]. The fuzzy logic implies human-like reasoning for determining the optimum solution. Unlike classiclogicsystemswherethevaluesareconsideredonly exact (i.e. true or false), fuzzy systems allow vague representation via fuzzy sets of the input values [3]. The inferenceinfuzzysystemsusesasetof pre-definedIF-THEN rulestodecidetheoutputvaluefromtheinputs.Anexample ofafuzzyrulewouldbe;IFtheTemperatureisCOLDTHEN Run Time is SHORT [4]. The output of a fuzzy system is defuzzified toa crisp value thatcan be used in real-world applications.Themainadvantageofusingfuzzysystemsis that their structure is relatively simple and intuitive for humans. Also, the system can be easily adjusted and modified as required [5, 6]. The Adaptive neuro-fuzzy inferencesystem (ANFIS)isa hybridlearningsystemthat combines the fuzzy logic systems and neural network
characteristics [7]. The ANFIS modeling uses training data combined with a set of fuzzy logic rules to produce a machine learning model that can be used for making predictions of the output variable from the values of the inputvariables[8].Duetotheabilityofneuralnetworksto adjust and learn the data, the ANFIS approach can provide more powerful predictions compared to mere fuzzy logic systems[9].
Various studies have been reported in the literature that involvesusingANFISandfuzzylogicsystemsinair-cooling devices-related applications. For instance, Soyguder et al. [10] developed an expert system that includes ANFIS and fuzzylogicoptimizationtocontrolheating,ventilationand air-cooling (HVAC) systems. Their system mainly focused on controllingthehumidityandthetemperatureoftheHVAC. The obtained ANFIS models were validated and showed low error in terms of estimating the required parameters for controllingthesystem.

Inanotherstudy,Al-Jarrahetal.[11]developedanalgorithm viaANFISmodelingthatfocusedoncontrollingair-cooling systemsatdifferentpressurevalues.ThebuiltANFISmodel was evaluated and assessed using experimental test data. The predictions of the model were compared to the real values and the computed error parameters indicated a reliableandpredictivemodelformanagingtheperformance ofair-conditionersatdifferentpressurevalues.
In this study, we use the fuzzy logic system and ANFIS modelingmethodstodevelopasystemthatcanpredictthe optimum run time for air-conditioners using the current roomtemperatureandthedoorstateofthechamberasthe input variables. The current temperature of the room is a commonfactortoconsiderwhendeterminingtheoptimum runningtime.Also,consideringthatroomswithopeneddoor requirealongerperiodofaircoolingduetothefasterheat transfer, the door state was added as another factor for determiningtheruntime.
2. METHOD
Two different approaches were used to build a run time predictionsystemforair-coolingdevices,namelythefuzzy logicsystemandtheANFIS.Thedatasetusedcomposedof 100recordsoftemperatureanddoorstateasinputvariables
andtheoptimumruntimeofairconditionerastheoutput variable. The implementation of the software was carried out via the Python programming language, using mainly the NumPy package for array-based and numerical operations [12]. Also, the Matlab package was used for generating theplots of the results [13]. In the upcoming sections, a brief description o-f each method will be providedalongsidethe proceduresusedindevelopingthe systems.
2.1 Fuzzy Logic:
Thefuzzylogicsystemswork-flowcanbebroadlydivided intothreedistinctsteps,namely,thefuzzificationoftheinput, the application of the IF-THEN set of rules and the defuzzification step [3]. The steps of the fuzzy system are illustrated in Figure 1. In the upcoming sections, a brief descriptionofeachstepisprovidedalongsidetheprocedure appliedforthecurrentcase.
2.1.1 Input Fuzzification
Initially,asetoflinguisticvariablesisdefinedbasedon
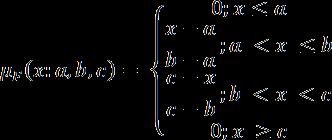

thecurrentapplication,thoselinguisticvariablesareusedin the IF-THEN rules evaluation [14]. For example, for the temperatureinputvariable,fivedifferentlinguisticvariables aredefined;VeryCold,Cold,Warm,HotandVeryHot.Based on the numerical value of the input temperature, each of those linguistic variables will be assigned a fuzzy value (rangingfrom0to1)[15].Forthispurpose,amembership function is used. There are various types of membership functions with different shapes such as triangular and trapezoidal membership functions [16]. The membership function converts the input value to a fuzzy value via a specificmathematicalequation,forexample,theequationof thetriangularmembershipfunctionisdepictedin(1)and (2).Threevalues representingtheupper,lowerandmedium values of each linguistic variable are also taken intoconsideration [17, 18]. Table 1 shows the linguistic variablesofthetemperatureinputvariableaswellasthea, b and c values required by the triangular membership functionequationforcomputingthefuzzyvalue.
In this study, three different membership functions were used and tested on the data, namely, the triangular, trapezoidalandGaussianmembershipfunctions,whichare widelyusedindifferentfuzzylogicapplications[19-21].The shape of each membership function is shown in Figure 2. Each membership function was assessed by making predictions of the output variable (the run time) and comparedwiththeexperimentaloptimumvalue.Themean absoluteerror(MAE)parameterwascomputedforeachone andcomparedwithoneanother.Thelowerthevalueofthe MAE parameter the more accurate and reliable the membershipfunctionisconsideredtobe[22].
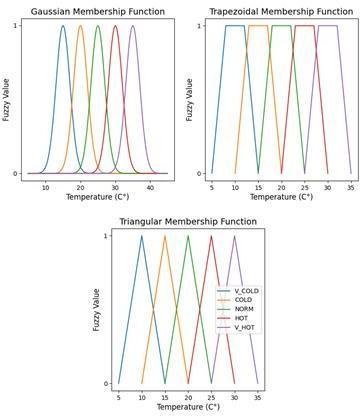
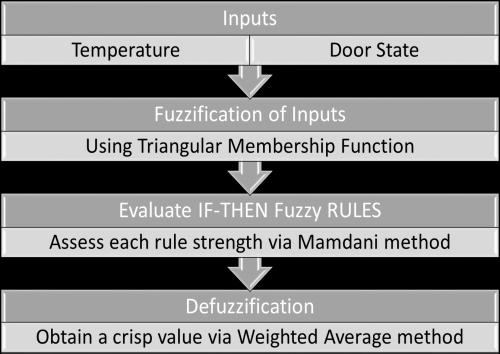 Fig-1:Work-flowdiagramofthefuzzylogicsystem.
Fig-1:Work-flowdiagramofthefuzzylogicsystem.
2.1.2.IF-THENrules
After the input fuzzification stage which determines the degreeofmembershipofeachinputlinguisticvariable,the next stage involves the evaluation of rules using IF-THEN statements[5].Forexample,IFTemperatureisCOLDAND DoorStateisOPENTHENRunTimeisLONG.Toassessthe strengthoftheserules,thedegreeofmembershipobtained fromtheinputfuzzificationisused.Thesetofrulesusedin thecurrentfuzzysystemisshowninTable2.
Table-2:Thesetofrulesimplementedinthefuzzylogic system
Where isthestrengthof eachruleandXiis the maximum value used in the triangular membership function.Thismethodyieldsresultsthataresimilartothe commonlyusedcenterofareamethods,however,itdemands lesscomputationsandiseasiertoimplement[25,26].
2.2.AdaptiveNeuro-FuzzyInferenceSystem(ANFIS)
TheANFISmethodcombinesthefuzzylogicsystemand theneuralnetworkapproachestoprovideamoreefficient predictionsystem[8].Inparticular,itusesthecharacteristics of the fuzzy logic including the input fuzzification via a membershipfunctionandtheIF-THENrulesevaluationas wellasthelearningabilitiesofneuralnetworks.Thismakes thesystemmoreaccurateandrobustwithhigherefficiencyin terms of learning the data and making better predictions [27].
2.2.1.Structureandlayers
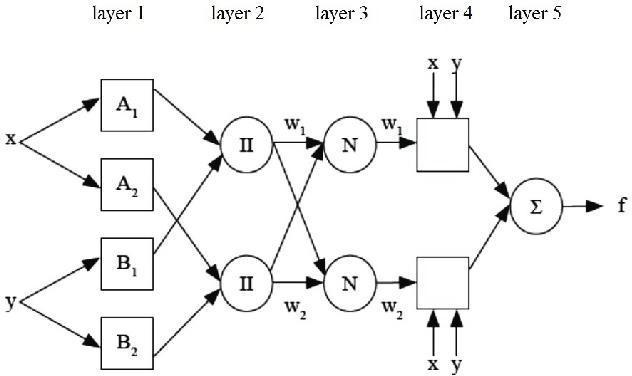
Considering that ANFIS is a neural network, it is composed of layers and nodes connected by edges that representweights.Theinputvariablesaretransferredand modifiedastheypassthroughthelayersofthenetworkto producetheoutputvalue.Theweightsareupdatedduring thetrainingprocessofthenetworktoadjustthedata[28]. The general structure of the ANFIS network is shown in Figure3.
Therearedifferentmethodstocomputethestrengthofeach rule. The method applied in the current system is the Mamdani method [23]. This method simply takes the minimumstrengthoftherulesintheinferencesystem.For example,intheruleIFTemperatureisVERYCOLDANDDoor Stateis OPEN THEN Run TimeisVERYLONG.IftheVERY COLD and OPEN fuzzy values are 0.7 and 0.4, the VERY LONG is assigned the minimum value which is 0.4. The outputofthisstageisastrengthvalueofeachrule,whichis used in the next stage which involves defuzzification to obtainthecrispoutputvalue[3,24].
2.1.3.Outputdefuzzification
Following the evaluation of the rules using the IF-THEN statements,theoutputisastrengthofeachlinguisticoutput variable, which is a fuzzy value. The last step is the defuzzificationoftheobtainedvaluestogetacrispoutput value [25]. There are various methods for performing defuzzification.Inthecurrentsystem,theweightedaverage method is adopted, which is simple and effective. The equation used for computing the crisp value using this methodisshownin(3)[26].

TheANFISstructureconsistsof5differentlayers.Thefirst layeristhemembershipfunctionlayer,inwhichtheinput variables arefuzzified via themembershipfunction equation toproducethemembershipdegreevalue.Thesecondlayer uses the output of the first layer (the membership degree values) to compute the firing strength of each linguistic variableinthesecondlayer,whichwillberequiredforthe rules evaluation by the subsequent layers of the network [29].Thethirdlayeristhenormalizationlayer,inwhichthe weightsarenormalized,thismakesthevalueofeachweight in the range [0, 1]. The fourth layer carries out the rules evaluation to determine the strength of each rule to the overalloutput.Thefifthlayerusesasummationmethodfor thevaluesobtainedfromthepreviouslayertodeterminethe finaloutputvalue[30].
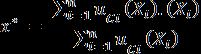
2.2.2.Modeltrainingandvalidation
TotrainandvalidatetheANFISmodel,theoveralldatawas dividedintotwodifferentsets,namely,thetrainingsetwhich wasusedfortrainingandthemodelandthetestsetwhich wasusedforevaluationofthemodelperformance[31].The training process of the ANFIS involves a running of the networkforseveralepochs(cycles),duringeachepoch,the error of the network prediction is computed via a cost function and the weights of the network are updated to minimize the error [32]. The root means squared error (RMSE)wasusedasthecostfunction[33].Todeterminethe optimumnumberofepochs,thenetworkswereallowedto runfor1000epochsandtheerrorwascomputedaftereach epoch. Thenumberof epochsthat correspondstothelowest error is considered to be the optimum epoch number for trainingthenetwork.
After training the model, the test set was used to assess the ability of the model to make predictions. The modelwasappliedtopredicttheruntimeofthetestset,and theerrorbetweenthemodel’spredictionandtherealvalue was measured. The coefficient of determination (R2), the MAE and the RMSE were calculated, which are commonly used validation parameters to assess the performance of machinelearningmodels[22,33,34].
3.2Hardwareimplementation
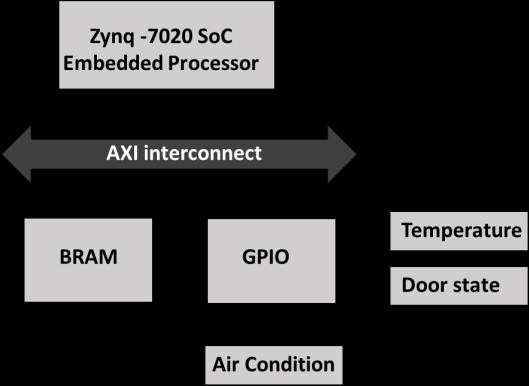
Considering thatthepurpose ofthe developedsoftwareisto controlaircoolingdevices,thedevelopedANFISmodelwas installed and tested on a Field-Programmable Gate Array (FPGA) embedded system [35]. The hardware part of the systemiscomposedofZynq-7020FPGAprocessorwiththe AXI BRAM memory and AXI GPIO, these components are availablein the Vivadointegrated development environment (IDE),thehardwarestructureisshowninFigure4.
For implementing the software part of the system, the softwaredevelopmentkit(SDK)toolswereused,whichare availableintheVivadoIDE[37].
3.RESULTS AND DISCUSSION
3.1.Fuzzylogicsystem
The three built fuzzy logic systems were evaluated by predicting the output variable (run time) using the temperature anddoorstateasinput variables.Theoutputof eachsystemwascomparedtotheoptimumruntimeandthe errorofpredictionwasmeasured.Theerrorplotofthethree systemsisdepictedinFigure5.Ascanbeseen,thetriangular membership function showed the lowest MAE value (4.766), which indicates a lower prediction error compared to the other two membership functions. The trapezoidal and Gaussian membership functions had higher MAE values (4.812 and 5.025, respectively) which reflects lower prediction accuracy compared to the triangular membership function.
The hardware architecture includes two ports, a memory blockRAMwith64KBsizeandBRAMController.BRAMdata is accessed within single cycle latency. Advanced Xilinx Interconnects (AXI) is introduced to the system hardware to act as bus system. The general purpose input/output (GPIO) unitprovidesahardwareinterfacebetweentheprocessor system AXI and the sensors (temperature and door state sensors)[35,36].
Chart-1:membershipfunction(MAE)
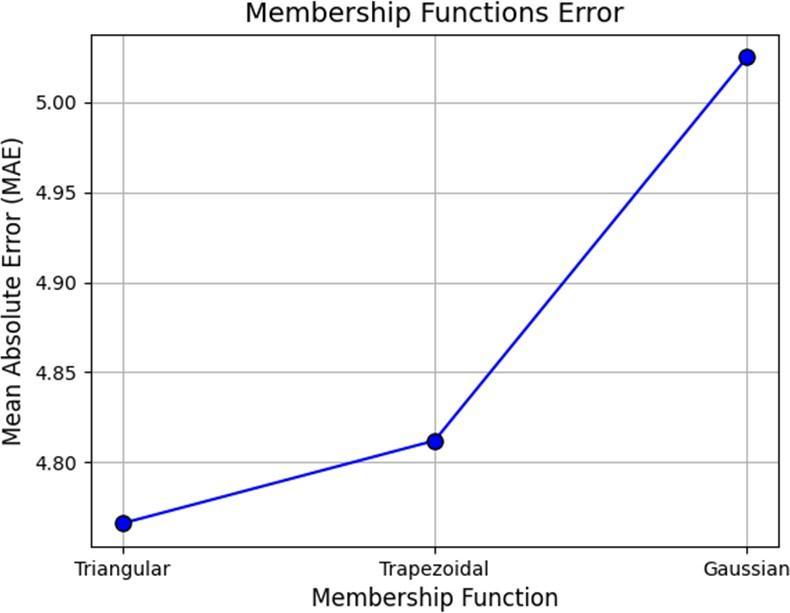
Considering that the triangular and trapezoidal membershipfunctionshavesimilarshapesaswellasinput parameters compared to the Gaussian membership function [18,19],itcanbeseenthattheyaremoresuitableforthis typeofapplication,astheybothshowedlowerandsimilar errorrate.Thetriangularmembershipfunctionwasfurther used as the membership function in the ANFIS model development as it displayed better prediction ability in comparisontotheothertwomembershipfunctions.
3.2. ANFIS model
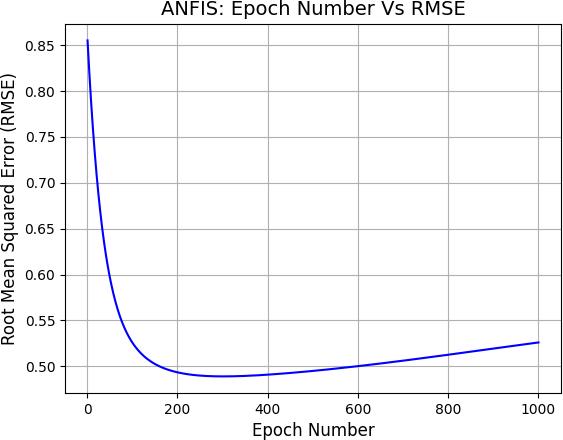
TheANFISmodelwasbuiltusingthetriangularmembership function and the set of rules previously described. The optimum number of epochs was determined to be 300 epochsbasedontheRMSEvalues.Figure6showsthechange intheRMSEvaluesasthenumberofepochsprogresses.As canbeseen,initiallytheRMSEvaluedropsfairlyquicklyas themodelislearningthedata,thenataroundepoch200the
 Fig-4 Thestructureofthedesignedhardware.
Fig-4 Thestructureofthedesignedhardware.
RMSEvaluebecomes morestable and drops moreslowly. At aroundepoch300theoptimumnumberofepochsisreached astheRMSEvaluebeginstoincreaseafterthisepoch,which indicatestheoccurrenceofover-fittingofthemodeldueto large number of epochs. The RMSE valuecontinues to increase afterward which is expected due toover-training of thenetwork.
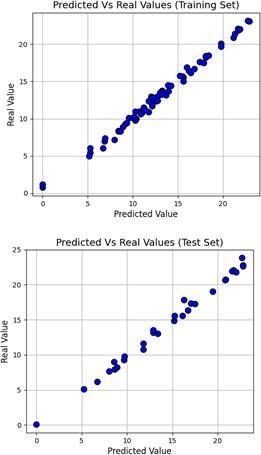
The model obtained at 300 epochs was validated by assessingitsabilitytopredicttheoutputvariable(runtime) ofthetestsetcompounds.Thevalidationparameterswere computed for the training and the test set compounds. However,thetrainingsetvalidationparameterscannotbe consideredreliableasthemodel wasfitandtrainedusing thisset.Ontheotherhand,thevalidationparametersofthe testsetareconsideredreliableasthedatawasnotinvolved inthetrainingofthemodel,andreflectsthemodel’sability to make predictions on unseen data. Table 3 shows the validationparametersandtheircorrespondingvalues.The R2valueforboththetrainingandtestsetwasclosetothe optimumvalueof1, whichshowsthatthemodelcanexplain the variancein the output variable using theinput variables. TheMAEvaluesforthetrainingandtestsetwere0.338and 0.413, respectively, which are both low and indicate the model can make accurate predictions. As expected the trainingsetMAE value wasslightlylowerbecausethe model wasfitusingthetrainingsetdataandhencethelowererror isexpected[34].TheRMSEvaluesshowedasimilartrendto theMAEvalues.Figure7showsthepredictedoutputbythe modelagainsttheactualvalueforboththetrainingandtest set.

Comparing the ANFIS model performance with the fuzzy logic system shows that the ANFIS model is significantly superior in termsofaccurateprediction.For instance,the MAEvaluesoftheANFISmodelandthebestobtainedfuzzy logicsystem(thetriangular membershipfunctionsystem) are0.338and4.766,respectively,whichreflectsthehigher accuracyoftheANFISmodel.Thiscanbeattributedtothe factthattheANFISmodelcanlearnthedataandadjusttoit to make better predictions due to its neural networks paradigm,whichismoreflexiblecomparedtothemerefuzzy logicsystemsthatuseonlyasetoffixedrulesevaluationto estimatetheoutputvalue[8,10,27].
4. CONCLUSION
The fuzzy logic system and ANFIS approaches were conducted to develop fuzzy logic systems and an ANFIS modeltopredicttheoptimumruntimeofairconditioners using the current temperature and door state as input variables. Three different membership functions were examined and their performance was assessed. The triangular membership function displayed better results compared to the trapezoidal and Gaussian membership functions. The obtained ANFIS model showed superiority overthefuzzylogicsystemsintermsofpredictionaccuracy as demonstrated by the lower error rates. Overall, the ANFISmodel proved to be highly efficient and accurate for application in run-time control of air-conditioning systems.
REFERENCES
[1] L.A.Zadeh,"Fuzzylogic,"Computer,vol.21,no.4,pp. 83-93,1988.
[2] F. M. McNeill and E. Thro, Fuzzy logic: a practical approach.AcademicPress,2014.
[3] K. Tanaka and K. Tanaka, An introduction to fuzzy logicforpracticalapplications.Springer,1997.
[4] J. C. Mugisha, B. Munyazikwiye, and H. R. Karimi, "Design of temperature control system using conventional PID and Intelligent Fuzzy Logic controller,"in2015Internationalconferenceonfuzzy theory and its applications (iFUZZY), 2015: IEEE, pp. 50-55.
[5] S. Basu, "Realization of fuzzy logic temperature controller," International Journal of Emerging Technology and Advanced Engineering, vol. 2, no. 6, pp.151-155,2012.
[6] A.D.M.Africa,A.M.J.L.Divino,andK.A.B.HartiganGo, "Fuzzy Logic Temperature Control: A feedback control system implemented by fuzzy logic," InternationalJournal,vol.8,no.5,2020.
[7] J.-S. Jang, "ANFIS: adaptive-network-based fuzzy inferencesystem,"IEEEtransactionsonsystems,man, andcybernetics,vol.23,no.3,pp.665-685,1993.
[8] D. Karaboga and E. Kaya, "Adaptive network based fuzzyinferencesystem(ANFIS)trainingapproaches:a comprehensive survey," Artificial Intelligence Review,vol.52,no.4,pp.2263-2293,2019.
[9] T. Mote and S. Lokhande, "Temperature control system using ANFIS," International Journal of Soft Computing and Engineering, vol. 2, no. 1, pp. 22312307,2012.
[10] S. Soyguder and H. Alli, "An expert system for the humidity and temperature control in HVAC systems using ANFIS and optimization with Fuzzy Modeling Approach," Energy and Buildings, vol. 41, no. 8, pp. 814-822,2009.
[11] R. Al-Jarrah and M. Al-Jarrah, "Developed adaptive neuro-fuzzy algorithm to control air conditioning systematdifferentpressures," InternationalJournal ofEngineering,ScienceandTechnology,vol.5,no.4, pp.43-59,2013.

[12] S.VanDerWalt,S.C.Colbert,andG.Varoquaux,"The NumPy array: a structure for efficient numerical computation," Computing in science & engineering, vol.13,no.2,pp.22-30,2011.
[13] J.D.Hunter,"Matplotlib:A2Dgraphicsenvironment," Computinginscience&engineering,vol.9,no.03,pp. 90-95,2007.
[14] F. Herrera, E. Herrera-Viedma, and L. Martínez, "A fuzzylinguisticmethodologytodealwithunbalanced linguistic term sets," IEEE Transactions on fuzzy Systems,vol.16,no.2,pp.354-370,2008.
[15] Z. Xu, "Group decision making with triangular fuzzy linguistic variables," in International Conference on Intelligent Data Engineering and Automated Learning,2007:Springer,pp.17-26.
[16] M.-S. Chen and S.-W. Wang, "Fuzzy clustering analysisforoptimizingfuzzymembershipfunctions," Fuzzysetsandsystems,vol.103, no.2,pp.239-254, 1999.
[17] W. Pedrycz, "Why triangular membership functions?," Fuzzy sets and Systems, vol. 64, no. 1, pp.21-30,1994.
[18] O. A. M. Ali, A. Y. Ali, and B. S. Sumait, "Comparison betweentheeffectsofdifferenttypesofmembership functions on fuzzy logic controller performance," InternationalJournal,vol.76,pp.76-83,2015.
[19] A. Barua, L. S. Mudunuri, and O. Kosheleva, "Why trapezoidal and triangular membership functions work so well: Towards a theoretical explanation," 2013.
[20] J. Zhao and B. K. Bose, "Evaluation of membership functions for fuzzy logic controlled induction motor drive," in IEEE 2002 28th Annual Conference of the IndustrialElectronicsSociety.IECON02,2002,vol.1: IEEE,pp.229-234.
[21] A.M.Ajofoyinbo,V.O.Olunloyo,andO.Ibidapo-Obe, "On development of fuzzy controller: The case of gaussian and triangular membership functions,"
Journal of Signal and Information Processing, vol. 2, no.04,p.257,2011.
[22] C. J. Willmott and K. Matsuura, "Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance,"Climateresearch,vol.30,no.1,pp.7982,2005.
[23] A.FernándezandF.Herrera,"Linguisticfuzzyrulesin data mining: follow-up Mamdani fuzzy modeling principle," in Combining Experimentation and Theory:Springer,2012,pp.103-122.
[24] O. Cordón, "A historical review of evolutionary learningmethodsforMamdani-typefuzzy rule-based systems: Designing interpretable genetic fuzzy systems," International journal of approximate reasoning,vol.52,no.6,pp.894-913,2011.
[25] J. J. Saade and H. B. Diab, "Defuzzification techniques for fuzzy controllers," IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 30, no.1,pp.223-229,2000.
[26] F. Smith and Q. Shen, "Selecting inference and defuzzification techniques for fuzzy logic control," in UKACCInternationalConferenceonControl'98(Conf. Publ.No.455),1998,vol.1:IET,pp.54-59.
[27] M.Elsisi,M.-Q.Tran,K.Mahmoud,M.Lehtonen,and M. M. Darwish, "Robust design of ANFIS-based blade pitch controller for wind energy conversion systems against wind speed fluctuations," IEEE Access, vol. 9, pp.37894-37904,2021.
[28] O.OpeyemiandE.O.Justice,"Developmentofneurofuzzy system for early prediction of heart attack," International Journal of Information Technology and ComputerScience,vol.4,no.9,pp.22-28,2012.
[29] O. C. Abikoye, E. O. Popoola, T. O. Aro, and V. O. Popoola,"AdaptiveNeuro-FuzzyInferenceSystemfor HIV/AIDS Diagnosis, Clinical Staging and Regimen Prescription," Computer Science & Telecommunications,vol.51,no.1,2017.
[30] A.Abdel-Aleem,M.A.El-Sharief,M.A.Hassan,andM. G. El-Sebaie, "Implementation of fuzzy and adaptive neuro-fuzzy inference systems in optimization of productioninventoryproblem,"AppliedMathematics
&InformationSciences,vol.11,no.1,pp.289-298, 2017.
[31] J.-S. Jang, "Input selection for ANFIS learning," in ProceedingsofIEEE5thinternationalfuzzysystems, 1996,vol.2:IEEE,pp.1493-1499.
[32] L.Naderlooetal.,"ApplicationofANFIStopredict crop yield based on different energy inputs," Measurement,vol.45,no.6,pp.1406-1413,2012.
[33] W. Wang and Y. Lu, "Analysis of the mean absolute error(MAE)andtherootmeansquareerror(RMSE) in assessing rounding model," in IOP conference series:materialsscienceandengineering,2018,vol. 324,no.1:IOPPublishing,p.012049.

[34] H.DetteandA.Munk,"Validationoflinearregression models,"AnnalsofStatistics,pp.778-800,1998.
[35] M. R. Khalil and L. A. Mohammeed, "Embedded processor system for controllable period-width multichannel pulse width modulation signals," TELKOMNIKA (Telecommunication Computing ElectronicsandControl),vol.19,no.1,pp.220-228, 2021.
[36] G. Nhivekar, S. Nirmale, and R. Mudholker, "Implementationoffuzzylogiccontrolalgorithmin embedded microcomputers for dedicated application," International Journal of Engineering, ScienceandTechnology,vol.3,no.4,2011.
[37] T.Feist,"Vivadodesignsuite,"WhitePaper,vol.5,p. 30,2012.
