Issuu

BUTLLET Í

DE LA SOCIETAT CATALANA DE MATEMÀTIQUES

Institut d’Estudis Catalans

Volum 33 ● Número 1 ● Juny 2018

BARCELONA 2018

©delsautorsdelsarticles

EditatperlaSocietatCatalanadeMatemàtiques ﬁlialdel’Institutd’EstudisCatalans CarrerdelCarme,47 08001Barcelona

Textrevisatlingüísticament perlaUnitatdeCorrecciódelServeiEditorialdel’IEC.

Imprèsa Ediciones Gráficas Rey, SL

ISSN:0214-316-X DipòsitLegal:B19272-1987

Sónrigorosamentprohibides,sensel’autoritzacióescritadelstitularsdel copyright,lareproducciótotaloparciald’aquestaobraperqualsevolprocedimentisuport,incloent-hilareprograﬁa ieltractamentinformàtic,ladistribuciód’exemplarsmitjançantllogueroprésteccomercial,la inclusiótotaloparcialenbasesdedadesilaconsultaatravésdexarxatelemàticaod’Internet. Lesinfraccionsd’aquestsdretsestansotmesesalessancionsestablertesperleslleis.

ButlletídelaSocietatCatalanadeMatemàtiques Vol.33,núm.1,2018

Índex

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi L’aportaciódeVicentCasellesalmóndelesmatemàtiques il’aplicacióalprocessamentd’imatges..............................................5

JoanCarlesNaranjo

PonceletalapresódeSaratov......................................................43 XavierXarles Elsprimers,desvelats...............................................................57

ButlletídelaSocietatCatalanadeMatemàtiques Vol.33,núm.1,2018.Pàg.5–41. DOI:10.2436/20.2002.01.78

L’aportaciódeVicentCasellesalmón delesmatemàtiquesil’aplicació alprocessamentd’imatges

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

Resum: Enaquesttreballesfaunrepàsdelescontribucionsmésimportantsde VicentCasellesalcampdelesmatemàtiquesilasevaaplicacióalsmodelsdeles imatges.Lessevesaportacionsvarencobrirtotunventallmoltample,desdelarecerca mésbàsica,coméselcasdelasevacontribucióalesEDPnolinealsial’estudianalític delmodeldelavariaciótotal(TV),finsalesaplicacionsalprocessamentd’imatges.Les seccionscorresponen,encertamanera,alesàreesenlesqualsvatenirunaparticipació méssignificativa.Mésconcretament,enlapartderecercabàsica,lesaportacions enl’estudidelfuncionaldelavariaciótotal,lesequacionsquasilinealsfortament degeneradesilesequacionsambfluxlimitat.Ienlapartdelesaplicacionsalcamp delprocessamentd’imatges,hemtriattrestemesenelsqualsCasellesvacontribuir demaneramoltsignificativa:ladetecciódecontorns,elproblemadelainterpolacióo inpainting ilaformalitzaciómatemàticadelateoriadelcolor.

Paraulesclau: anàlisifuncional,variaciótotal,EDPnolineals,processamentd’imatges, detecciódecontorns,interpolació,teoriadelcolor.

ClassiﬁcacióMSC2010: 68T99,46Txx,35K93.

1Introducció

perColomaBallester

Aquesttreballpreténserunaaproximacióalesaportacionsmésimportantsque ensvadeixarVicentCasellesenlasevaexcepcionalobracientíficamatemàtica. L’obradeCasellesvaserimmensailessevesaportacionsvarencobrirtotun ventallmoltample,desdelarecercamésbàsicafinsalmóndelesaplicacions enelcampdelprocessamentd’imatges.CommoltbédiuJ.M.Mazónalfinal delasevapartdinsaquestmateixtreball,alasecció2,VicentCasellestenia unaculturaiunaformaciómatemàtiquesexcepcionals;vaserunad’aquestes personesquedeixenpetjada,unacapacitatdetreballinfinita,enpartdegudaal seuinterèsperqualsevoltemaqueselipoguésplantejar.Però,almateixtemps, eraunapersonamolthumanaigenerosa,ambquieraagradablecompartir puntsdevistasobretemeshumansicientífics.

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

Desdelpuntdevistadelarecercabàsicaienlasevaprimeraetapa,vegeu lasecció2,elsseusesforçosesvarendirigircapalateoriad’operadors positiusenreticlesdeBanachienlesequacionsenderivadesparcialsno lineals.Posteriorment,imotivatperlesaplicacionsalcampdelarestauració d’imatges,ensvaendinsar,juntamentambF.AndreuiJ.M.Mazón,enl’estudi analíticsobreelfuncionaldelavariaciótotal(TV).Lessevesaportacionsvaren serclauperentendreelcomportamentilespropietatsdelﬂuxvariaciótotal. Dinslamateixalínia,elsseusestudisenelcampdelesequacionsquasilineals fortamentdegeneradesienlesequacionsambﬂuxlimitatvarensermolt importantsperdesencallaralgunsproblemesclàssicsenaquestcamp.

D’altrabanda,elsgransavençosenelcampnoudelprocessamentide l’anàlisimatemàticad’imatgesnoespodenentendresenselesaportacions deCaselles.Unaimatgeenescaladegrisos f potmodelar-secomunafunció escalardeﬁnidaenundomini R delplaeuclidià, f : D→ R.Enelcasd’una imatgeencolor,lafunció f seriaunafunciódeﬁnidaeneldomini R delpla, queagafaelsseusvalorsdins R3 .

Enl’aplicaciódelesmatemàtiquesalprocessamentd’imatges,undelsprimersproblemesquevaconsiderarCasellesvaserladetecciódecontornso corbesqueseparenregionshomogèniesd’unaimatge;vegeulasecció4.Laseva solució,donadaperunageodèsicaenunespaideRiemannilasevaanàlisimatemàtica,vaserfonamentaleneltractamentdelproblema.Unaaltraaplicació alcampdelesimatgesenlaqualvatreballarvaserlainterpolaciód’imatges (problemadel’inpainting);vegeulasecció3.Enaquestaaplicació,esconeixel valord’unaimatgeenunsubconjuntdelseudominiillavorselproblemaés trobarunaimatgedeﬁnidaentoteldominiiquecoincideixiambladonadadins elsubconjuntoriginal.VicentCasellespotserconsideratundelsfundadors d’aquestcamp,alqualvacontribuirengranmanerabasant-seenlainterpolació geomètricaitextural.Finalment,hemconsideratl’aplicacióalesimatgesencolor,alaqualCasellesvadonarunimpulsenlasevaformalitzaciómatemàtica; vegeulasecció5.Enunprimertreball,CasellesiSapirovanutilitzarprincipis variacionalsperferunainterpretaciónovadel’equalitzacióperhistograma, quevaserutilitzadaposteriormentperconstruirunmarcvariacionalperal realçamentdelcolorinspiratenlespropietatsdelsistemadelavisióhumana. DosmomentsimportantsenlavidaacadèmicadeVicentCaselles.

1.1Ressenyabiogràﬁca

VicentCasellesCostavanéixerl’agostdel1960aGata,pobledelacomarcade laMarinaAlta,alPaísValencià,benalavoradelMontgó,lamuntanyamítica quedominalacomarcailasevamariperalaqualVicentteniatantd’apreci. Elseuparetreballavaalcampilasevamareregentavaunatendafamiliarde queviuresiarticlesdiversosenlaqualespodiatrobardesdemoixamaialtres saladuresdepeixfinsamitjons.Enlasevainfànciaijoventutfeiatotelque estavaalessevesmansperaconseguirbonaliteraturaibibliografiaespecialitzada,totilesdificultatsdel’Espanyad’aquellaèpoca.Vatreballaralcamp ialacooperativadeGataalsestiusperpagar-seelsestudisielsllibres.Va acabarlallicenciaturadematemàtiquesalaUniversitatdeValènciai,posteriorment,el1985,eldoctorat;vaobtenirtantelPremiExtraordinariFideCarrera comeldedoctorat.Vacontinuarestudiantendiversesuniversitatseuropees:a Alemanya,alMathematischesInstitutderUniversitätTübingen,iaFrança, al’UniversitédeFranche-Comté(Besançon)ial’UniversitéParis-Dauphine.CasellesvaocuparplacesenlesuniversitatsdeValència,Franche-Comté,Illes BalearsiPompeuFabra,oneracatedràticdematemàticaaplicada,ivafer estadesdediversaduracióendiversoscentrescomUCLA(EUA),l’Université Paris-Dauphine,l’ÉcoleNormaleSupérieureParis-Saclay(abansENSCachan), l’InstitutHenriPoincaré,l’UniversitéParis-VI(totesaFrança)il’Universität Tübingen(Alemanya).Enparal lelalasevaactivitatinvestigadoraidocenta laUPF,CasellesvaserdirectorcientíficdelGrupd’ImatgeiGràficsdelCentre TecnològicBarcelonaMedia(aradinsEurecat),desd’on,enrelacióestretaamb elsectorempresarial,vadesenvoluparnovesaplicacionsdelprocessament d’imatgesadiversossectorsindustrialscomaralatelevisióoelcinemadigitals.Ambtresllibrespublicats,mésdedos-centsarticlesd’investigació,dues patents,ladirecciódedissettesisdoctoralsil’edicióderevistesdeprestigii referènciainternacional,elstreballsdeVicentCaselleshantingutunainfluènciaconsiderableilihandonatunreconeixementinternacional.Provad’aixòés quevaserconferenciantconvidatencongressoscoml’InternationalCongress ofMathematiciansel2006,l’InternationalCongressonIndustrialandApplied Mathematicsel2011iel6èEuropeanCongressofMathematicsel2012.Caselles varebrenombrososreconeixementsalasevaactivitat.Aescalanacional,cal destacarlaDistinciódelaGeneralitatdeCatalunyaperalaInvestigació2002; elPremiFerranSunyeriBalaguer2003;ladistincióICREAAcademia2009.A escalainternacional,podemdestacarelSIAM(SocietyforIndustrialandApplied Mathematics)OutstandingPaperPrize2008(perl’aportaciódelfonamentteòric delmètodeproposatperRudin,OsheriFatemi,detallatenlasubsecció2.2); elTestofTimeAwarddelaInternationalConferenceonComputerVision el2011(peltreball«Geodesicactivecontours»detallatenlasecció4;elguardó reconeixlesaportacionsrellevantsquehantingutimpactealllargdeltemps enl’àmbitdevisióperordinador);elSIAMActivityGrouponImagingScience prizeel2012(perl’articleaIEEE-PAMI«Aperceptuallyinspiredvariational frameworkforcolorenhancement»detallatenlasecció5),il’AdvancedGrant

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

del’EuropeanResearchCouncilaﬁnalsdel2012,perdesenvoluparunprojecte d’investigacióquenovapoderacabarjaquevamorirel14d’agostdel2013. D’altrabanda,VicentCasellesestavaentusiàsticamentimplicatenladocència, atotselsnivells,tantenl’aprenentatgeactiuiprofundenelsgrausialtres titulacions,d’algunadelesqualsenvaliderarlacreació,comenprogramesde doctoratienelsestudiantsdedoctorat.

Esquerra:El1984o1985,ambJoanBisquertalacasetadelsMiralbons. Dreta:Al6èEuropeanCongressofMathematicsaCracòviael2012.

Coms’haesmentat,l’obracientíficamatemàticadeVicentCasellesésexcepcional.Lapersonatambéhoera.Elseuentusiasme,culturaihumanitat sónqualitatsdeCasellesdestacadespelsqueelconeixien.Peraixòacabarem aquestabreuressenyabiogràficaambuntextseuescritamàundiaquejugàvemaescriurebiografies.Entred’altres,livaigdemanarqueescrivíssobresi mateixivaredactarelquesegueix.M’hasemblatadequatilleialambquiera ellrecuperaraquesttext,transcritsensecapmodificació:

VicentCasellesCostavanéixeraGatael10d’agostde1960.Malgratqueavui totestrobacercantainternet,ésacteprotocolarifer-neunsketchdelaseva biografia.VicentésprofessordeMatemàticaAplicadaalaUniversitatPompeu Fabra(Barcelona).Desprésdeseguirl’escolaaGatafinsals10anys,vaseguir l’acadèmiadepreparaciódelbatxilleratlliurequehihaviaaGata,dels11als 13anys.Dels14anysifinsquasials17vacursarelbatxilleratal’InstitutRoc ChabàsaDénia.Al’octubrede1977vaentraralaFacultatdeMatemàtiques delaUniversitatdeValència,onvaseguirelprimercursdeformapresencial. Percircumstànciespersonals,elscursossegon,terceriquartelsvaseguirdes delacasaquetenialafamíliaalcarrerSignes69,onaraviuelseugermà JuanCasellesCosta.Aquestsvarenseranysdelamàximallibertatbàsicament dedicatsal’estudiiapassejosvespertinsperlaFontdelaMata(quintresor)junt ambenVicentSabater,onvaigpoderdisfrutardelalecturadelsgransclàssics delesmatemàtiquesidelafísica,gustquesemprem’haacompanyat.Elcinquè curs,el1981–1982,vatornaralauniversitat.Durantelstresanyssegüents,va cursareldoctorat,estudiantfísicaalmateixtemps.Enaquestsanys,vaigfer coneixençadeJoanBisquert,actualmentunfísicaplicatalaUniversitatJaumeI

deCastelló,ambmoltaaltaconsideració.Durantelsestius,jotreballavaala casetadelsMiralbonsquemiraalMontgó(quintresor)iJoanveniatambéa estudiarallà.Ellhocomparavaal’esglèsiadelParePere.Al’acabareldoctorat, vapassardosanysaTübingen(Alemanya),dosanysaBesançon(França),un anyaMadrid(fentelserveimilitar),miganyaParís,vuitanysaPalma,i,a partirdelcurs1999–2000,alaUniversitatPompeuFabra,essentalavegada asiduvisitantdeParísiPisa.AlaUPFhatreballatdesdellavors.Actualmentés tambédirectorderecercadelGrupd’ImatgedelaFundacióBarcelonaMedia, ontreballaendiversosprojectesindustrialsambempreses,entreellesamb Mediapro(queté,perexemple,LaSexta).

2L’aportaciódeVicentCasellesenlarecercabàsicadeles matemàtiques perJoséM.Mazón

2.1Introduccióal’obradeVicentCaselles

VoldriacomençaragraintalaSocietatCatalanadeMatemàtiquesl’oportunitat queembrindaperescriureaquestarticlesobreunapartdel’obramatemàtica deVicentCaselles,aquellaqueésmésproperaalsmeusinteressosinvestigadors,enunapartdelaqualvaigtenirelprivilegidecol.laborarambell.

Uncopacabadalallicenciatura,VicentCasellesvacomençaraferlatesi doctoralsotaladirecciód’AntonioMarquina.Vadefensarlatesi,titulada «SobrelateoriadeRadon-NikodymiPerron-Frobeniusdelsoperadorspositius» el1985.Vaigtenirl’honordeformarpartdeltribunalquelavajutjar.Aquesta tesis’emmarcaenelcampdel’anàlisifuncional,mésconcretamentenla teoriad’operadorspositiusenreticlesdeBanach.Enaquesttreballjas’hi veulaprofunditatdelsraonamentsmatemàticsdeCaselles.Finalitzadala tesi,CasellesvaferunaestadapostdoctoraldedosanysalaUniversitatde Tübingen,onvaseguirtreballant,ambelgrupdelprofessorSchaefer,en lateoriad’operadorspositiusenreticlesdeBanachilasevarelacióambla geometriadelsespaisdeBanach.Algunesdelessevescontribucionsaaquesta teoriaestanrecollidesenlespublicacions[49,50,51,52,53,54,55,7].

El1987CasellesesvatraslladaraBesançon,onvaromandretresanys. Aquícomença,sotaladirecciódelprofessorPhilippeBénilan,atreballaren elcampdelesequacionsenderivadesparcialsnolineals,campquemaiva abandonarencaraqueméstardesdediquésmoltintensamentatreballar enelprocessamentd’imatges.EnlasevaetapadeBesançonobtéresultats importantssobreequacionsdeprimerordreiladualitatentrelleisescalars deconservacióilesequacionsdeHamilton-Jacobi[69, 56].Enaquestaprimera etapadecanvicapalesEDPnolinealsCasellesnoabandonalarecercaenteoria espectrald’operadorspositius.Enaquestcampvadirigirlasevaprimeratesi doctoral,aFrancescAràndiga,ambelqualvacontinuartreballantenaquest temaﬁnsa1994.AlgunsdelsseusresultatsambAràndigaestrobena[19, 20].

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

El1990CasellestornaaEspanya,mésconcretamentalaUniversitatde lesIllesBalears,onaviatvaobtenirunaplaçadeprofessortitularionva romandrenouanys.EnelDepartamentdeMatemàtiquesiInformàtica,alqual esvaincorporar,hihaviaunpetitgrupderecercaenprocessamentd’imatges, lideratpelprofessorfrancèsJean-MichelMorel.Casellesaviatvacomençar atreballarenaquesttema,hivatrobarelqueestavabuscantdesdelaseva èpocad’estudiant:untemadegranprofunditatmatemàticaiambaplicacions pràctiquesimportants.Desdellavorsvadedicarelsseusmàximsesforçosa treballarenaquestcamp,onvaarribaraserundelslídersinternacionals.

2.2L’aportaciódeVicentCasellesalmodeldelavariaciótotal(TV)

Elsprimersaintroduirlavariaciótotalenmodelsderestauraciód’imatges vanserL.Rudin,S.OsheriE.Fatemienelseutreball[98].Alaﬁdelsanys norantahihaviaunaliteraturaextensasobremètodesnumèricsiaplicacionsal processamentd’imatgesdelsnousmodelstractatsa[98],perònohihaviacap resultatanalític.FuensantaAndreuijovamtenirelprivilegidetreballaramb Casellesenelproblemadelaminimitzaciódelavariaciótotal.Laprincipal diﬁcultatambquèensvamtrobarvaserferunainterpretaciócorrectade l’operadordiferencial

queapareixenl’equaciód’Euler-Lagrangeassociadaalfuncionald’energiadel modeldeL.Rudin,S.OsheriE.Fatemi.Desprésd’unsanysdetreball,a[5], aconseguimdonarunconcepteadequatdesoluciódelproblemadeNeumann associatal’operador (1),peralqualproveml’existènciailaunicitatdesolucions,aixícomelcomportamentasimptòtic.Amés,trobemsolucionsexplícites queposendemanifestladinàmicaespecialdelessolucionsd’aquestproblema. Posteriorment,imotivatsperunmodelinteressantperalproblemad’inpainting (reconstrucciód’unapartd’unaimatge),introduïta[24],estudiemelproblema deDirichletassociatal’operador (1).Lespropietatsqualitativesdelfluxvariació totallesestudiema[6],encol laboracióambIldefonsoDíaz,onestablimqueles solucionsdelproblemadeNeumannaconsegueixenlamitjanadeladadainicial entempsfinit,fenomenquejas’haviaobservatnumèricament.Elproblemade CauchyelvaestudiarCasellesa[31],encol.laboracióambGiovanniBellettini iMatteoNovaga,on,amésdeveurequeelproblemaestàbenposatenel sentitdeHadamard,s’estudial’evoluciódelsconjuntsdeperímetrefinit,i esdemostraqueenelcasbidimensionalelsconjuntsqueevolucionensense deformar-sesónelsdenominats conjuntscalibrables enlateoriageomètricade lamesura.

Elsconeixementsitècniquesobtingutsenl’estudidelﬂuxvariaciótotalens vanpermetreestudiara[8]i[9]problemesparabòlicsquasilinealsassociats afuncionalsd’energiaambcreixementlinealal’inﬁnit,mésconcretament

problemesdelaforma

= div a(x,Du) a Q = (0, ∞) × Ω, u(t,x) = ϕ(x) sobre S = (0, ∞) × ∂Ω, u(0,x) = u0(x)x ∈ Ω,

amb a(x,ξ) =∇ξ f(x,ξ),on f ésunfuncionalambcreixementlinealen ξ quan ξ →∞.Undelsexemplesmésrepresentatiuséselfuncionald’àrea f(ξ) = 1 + ξ 2,l’operadordiferencialassociatdelqualéseldelessuperfíciesmínimes.

Elsresultatsanteriorsielsobtingutssobreelﬂuxvariaciótotalsónlabase delamonograﬁa[10],amblaqualel2003vamobtenirelpremiFerranSunyer iBalaguer.

Casellesteniaungranconeixementdelespropietatsfinesdelesfuncionsde variaciófitadaidelateoriageomètricadelamesuraienaquestcampvacollaborarintensamentambunadelesescolesméspotents,ladePisa,fundada perI.deGiorgi.Lasevaprimeracol laboracióambaquestaescolaésuntreball important,encol.laboracióambLuigiAmbrosio,SimonMasnouiJean-Michel Morel[4],enelquals’estudialanociódeconnexiódesdelpuntdevistadela teoriageomètricadelamesura,ielsresultatsteòricsques’obtenens’apliquen aproblemesdelprocessamentd’imatges.Desprésd’aquestaprimeracol.laboracióambmatemàticsdel’escoladePisa,larelaciódeCasellesambmembres d’aquestaescolahaestatmoltintensaifructífera,especialmentambGiovanni BellettiniiMatteoNovaga,ambelsqualsa[32]obtenensolucionsexplícitesdel problema ∆1u = u,solucionsquedescriuenelcomportamentasimptòticde lessolucionsdelproblemadeCauchyassociatalfluxvariaciótotal.Com unaaplicacióobtenensolucionsexplícitesdelproblemade denosing (netejat d’imatges).AlgrupanterioresvaincorporarAntoninChambolledel’École Polytechniqueiambellsobtédostreballsimportants[29, 30]sobrel’evolució desubconjuntsconvexsde RN permitjàdelacurvaturamitjanacristal.lina, i.e.,atravésdelfluxgradientdelfuncionald’energiadesuperfíciedefinitper Pϕ(E) := ∂E ϕ0(νE )dH N 1 (νE éslanormalunitàriaa ∂E),

on ϕ0 : RN → [0, ∞) ésunafunciópositivamenthomogèniadegrau1talque {ϕ0 ≤ 1} ésunpoliedre.A[29]provenl’existènciaiunicitatdesolucions d’aquestfluxquanladadainicialésunconjuntcompacteconvexadmissible de RN .Comaconseqüència,resolenunproblemaproposatperAlmgren-TaylorWangel1993[1].A[30],entrealtresresultats,esdemostraquesiladada inicialésuncosconvex C i C(t) éslasoluciódelfluxanterior,imposantque espreservielvolum,estéque C(t) convergeixrespectedeladistànciade Hausdorff,quan t →∞,auntraslladatdelaformadeWulffdevolum |C|, i.e., aunasoluciódelproblemademinimització

inf{Pϕ(E) : |E|=|C|}, on ϕ(ξ) := sup{ η,ξ : ϕ0(η) ≤ 1}.

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

Unaltretreballinteressant,sorgitdelasevacol.laboracióambChambolle iNovagaés[31],enquèestudienlaregularitatdelessolucionsdelproblema d’eliminaciódelsorolld’unaimatgepermitjàdelavariaciótotal.Mésprecisamentobtenen,peradimensionsmenorsoigualsque7,quesi u ésunmínim delfuncional

i f ∈ C 0,β(Ω),0 ≤ β ≤ 1,aleshores, u ∈ C 0,β(Ω).

Encol.laboracióambundelsseusdoctorands,FrançoisAlter,iambAntonin Chambolle,a[3]generalitzenelsresultatsbidimensionalsobtingutsa[31]ifan unacaracteritzaciódelsconjuntsconvexoscalibrablespermitjàdelacurvatura delasevafrontera.

Enlateoriadelsconjuntsconvexos,unaclassemoltimportantsónels anomenats conjuntsdeCheeger,quesónelsqueminimitzenlaproporció entreelseuperímetreielseuvolum.Mésprecisament,donatunconjuntﬁtat Ω ⊂ RN ,lasevaconstantdeCheegeresdeﬁneixcom

UnconjuntdeCheegerde Ω ésqualsevolconjunt G ⊆ Ω queminimitza(3).

ElsconjuntsdeCheegertenenunpaperimportantenmoltscamps,per exemple,enelcomportamentasimptòticdelessolucionsdel’equaciód’evolucióambcurvaturamitjanaconstant,enelproblemad’autovalorsassociatalflux variaciótotal,enproblemesdedissenyòptim,etc.Elproblemadelaunicitat delsconjuntsdeCheegereraunproblemaobertimportant.Aquestproblema vaserresoltperCaselles,ChambolleiNovagaa[62],quevansuposarque Ω ésuniformementconvexideclasse C 2.Lasoluciódefinitivavaserobtinguda perCasellesencol.laboracióambFrançoisAlter,a[2],enquèprovenquedins decadacosconvexnotrivialde RN existeixunúnicconjuntdeCheegerque, amés,ésconvexideclasse C 1,1.L’extensiód’aquestresultatalcontextdels espaisdeGauss n-dimensionalsialsespaisdedimensióinfinitadeWienerva serdutaatermea[70].

2.3L’estudidelesequacionsquasilinealsfortamentdegenerades

Desprésdelsnostrestreballssobrelavariaciótotalilesequacionsdetipus (2), comencemaestudiarequacionsquasilinealsfortamentdegenerades,l’operador diferencialdelesqualsésdelaforma div a(u,Du) amb a(z,ξ) =∇ξ f(z,ξ),i ambellagrangià f quesatisfà,fonamentalment,lacondició

C0 ξ − D0 ≤ f(z,ξ) ≤ M( ξ + 1). (4)

Equacionsd’aquesttipusapareixenenmoltsproblemesfísics,com,perexemple,enlafísicadelplasma.Noobstantaixò,laliteraturamatemàticasobre aquesttipusd’equacionserapràcticamentinexistentilaqueexistia,dostreballsdeMichaelBertschiRobertaDalPasso[37, 74]iundePhilippeBlanc[39],

eraendimensió1.Perestudiaraquestproblemausemelmarcdelesequacionsd’evoluciógovernadesperoperadorsacretius,amblaqualcosavamhaver d’estudiarprimeramentelproblemael.líptic.Aixòhovamfera[11].Elproblema mésdifícilvaser,denou,interpretarcorrectamentl’operadordiferencial.Pera aixòvamhaverdedesenvoluparuncàlculfuncionalinspiratenelsfuncionals d’energiarelaxatsestudiatsperl’escoladecàlculdevariacionsdePisa.Ambels resultatsd’aquesttreballielteoremadeCrandall-Liggett,aconseguima[13] demostrarqueelproblemadeNeumannassociatal’operador div a(u,Du) està benposat.

Unavegadaresoltaquestproblema,vamtenirconeixementdeltreballde YannBrenier[40],enelqualdedueix,permitjàdelateoriadeltransport optimaldemasses,iusantunafunciócostquepenalitzal’evolucióauna velocitatmésgranqueunaconstantpreﬁxada,l’equacióquevadenominar equaciórelativistadelacalor.L’equacióvaserproposadaprimeramentper PhilippeRosenaua[97],perdonarunarespostaalproblemadelavelocitatde propagacióinﬁnitadel’equaciódelacaloridelesequacionslinealsdedifusió. Aquestaequació

téassociatellagrangià

quenosatisfàlacondició (4).ComassenyalaBreniera[40],l’equaciórelativista delacalorésunaentrelesnombroses equacionsdedifusióambﬂuxlimitat usadesenlateoriadelaradiacióhidrodinàmica[91],unexempledelaqualés

quevaserproposadaperR.Wilson.

A[12]estudiemelproblemadeCauchyperaunaclassegeneraldeproblemesquasilinealsfortamentdegeneratsdelaforma

on0 ≤ u0 ∈ L

=∇ξ f(z,ξ).Lahipòtesiprincipalsobre f ésquetinguielcreixementlineal

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

peracada (z,ξ) ∈ R × RN ,ifuncionscontínuesipositives C0, D0, M0, amb C0(z)> 0peracada z ≠ 0.Ellagrangià (6),aixícomelcorresponenta l’equació (7),satisfà (9).Comaconseqüènciadelsresultatsde[12],trobemque elproblemadeCauchyperal’equació (5) estàbenplantejat.Encol laboració ambSalvadorMoll,provema[16]quelessolucionsdelproblemadeCauchyper al’equació (5) tenenvelocitatdepropagació c,queéslaconstantqueapareix al’equació,ia[17]veiemqueelproblemadeDirichletperal’equació (5) està benposat.

Heurísticamentveiemquesiesfatendir c →∞ al’equació (5),s’obté l’equacióclàssicadelacalor.Lademostraciórigorosa,defet,estàllunydeser trivialivaserobtingudaperCasellesa[57].

Elconceptedesoluciód’entropiaperalproblemadeCauchyperal’equació (5) ésbastantcomplicatitècnic;penseu,perexemple,queladerivada temporalésunelementdeldualdel’espai L1(0,T ; BV(RN )) jaquelessolucions tenenfrontsdediscontinuïtatqueesmouenalavelocitat c.Noobstantaixò,en l’article[14]esvanobtenirunsresultatsderegularitatquevanpermetreferuna caracteritzacióbastantnaturaldelessolucionsd’entropia.Casellesa[58]va milloraraquestresultativadeduirqueelconjuntdesaltconstadefrontsque espropaguenalavelocitatdonadaperunacondiciódetipusRankine-Hugoniot, cosaqueposademanifestelcaràcterhiperbòlicdel’equació(5).

Elprimermodeldefrontsdepropagaciópermitjàd’equacionsdereacciódifusióésladenominada equaciódeFisher-Kolmogorov ut = D∆u + ku(1 u), (10)

queigualquel’equaciódelacalortévelocitatdepropagacióinﬁnita.A[15]vam proposarcomamodelalternatiualclàssicdeFisher-Kolmogorov,l’equació

Demostremqueperadadesinicials0 ≤ u0 ≤ 1,elproblema (11) téunasolució d’entropiaúnica,lavelocitatdepropagaciódelaqualestàlimitadaper c. Usantelconceptedesoluciód’entropiaintroduïta[15],J.Campos,P.Guerrero, Ó.SáncheziJ.Solera[47]fanunestudidelesonesviatgeresde (11),enel casunidimensional,idemostrenquehihaonesviatgeresquesónsolucions d’entropiadiscontínuesiqueviatgenavelocitat c. UnaltredelstemesenquèCasellesvatreballarvaserenlesequacionsde difusióambﬂuxlimitatenmedisporososodedifusióràpida.A[59]estudiael problema

= div a(u,DΦ(u)) a QT = (0,T) × RN , u(0,x) = u0(x) pera x ∈ RN , (12)

on0 ≤ u0 ∈ L1(RN ) ∩ L∞(RN ), a(z,ξ) =∇ξ f(z,ξ),amb f quesatisfàcondicionsdeltipus (9) i Φ : [0, ∞) → [0, ∞) ésunafuncióestrictamentcreixentamb Φ(0) = 0, Φ, Φ 1 ∈ W 1,∞([a,b]),0 <a<b.Uncasparticularimportantés l’equació ut = α div

Λ(u)DΦ(u) 1 + β|DΦ(u)|2   (13)

peralaqualdemostrapropietatsderegularitaticaracteritzalacondició d’entropiamitjançantunacondiciódetipusRankine-Hugoniot,iobtéqueel frontdediscontinuïtatsdelasoluciód’entropiaesmouavelocitat v = Λ(u+(t)) Λ(u (t)) u+(t) u (t) .

Hihaduesmaneresd’escriureequacionsambﬂuxlimitatenmedisporosos odedifusióràpida,asaber: ut = div

. (14)

Lademostraciórigorosadelaconvergència,quan c →∞,delesequacions anteriorsalesequacionsclàssiquescorresponents ut = div(um 1Du),ut = div(uDum), (15)

respectivament,vaserfetaperCasellesa[60].A[46],vaestudiaralcostatde JuanCalvopropietatsderegularitatdelesequacions (14),itambévaveure queelproblemadeCauchyperal’equació (14) estàbenposatenelrangdela difusióràpida,0 <m< 1;elcasdemedisporosos, m ≥ 1,estàtractata[12].

A[18]esfaunestudinumèricdel’equació (14) queposaenevidènciaque l’evoluciódelessolucionsnumèriquesestàcaracteritzadapertresfases.Enla primera,elperﬁldelasoluciócanvia,peròelsuportnoesmou.Enunasegona fase,lasoluciódesenvolupadiscontinuïtatsdinsdelseusuportilespropaga entempsﬁnitcapalafrontera.Finalment,quans’haformatladiscontinuïtat desaltalafrontera,elsuportcomençaacréixeriapareixunfrontdiscontinu. L’estudinumèricdel’equaciórelativistadelacaloridel’equació (14),enelcas unidimensional,elvaduratermeCasellesalcostatdeJ.A.CarrilloiS.Moll a[48].Aquestestudivaserampliata[45].

L’estudidelesonesviatgeresperal’equació (14),ambuntermedereacció comeldel’equació (11),l’hanfetrecentmentJ.Calvo,J.Campos,V.Caselles, Ó.SáncheziJ.Solera[44],ihanobtingutquepera m> 1,amésdels tipusd’onesviatgeresqueestenenpera m = 1,apareixendosnoustipus d’onesviatgeres:unesquesóncontínuesperònosuausiunesaltresquesón discontínuesal’interiordelsuport,laqualcosaconstitueixunprimerexemple d’unasoluciód’unaequacióparabòlicanolinealambunadiscontinuïtata l’interiordelseusuport.Un survey excel.lentdelsresultatssobreequacions

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

ambﬂuxlimitatenmedisporososobtingutsperCasellesencol.laboracióamb elgrupderecercaenEDPdeGranada,estrobaa[43].

Amésdelamonografia[10],Casellesésautordeduesmonografiesmés, unaencol.laboracióambMarcBernotiJean-MichelMorel[33],sobretransport òptimenxarxes,enlaqualfanuntractamentmatemàticunificatdelsplansde tràfic;iunaaltraencol.laboracióambPasceleMonasse[71],sobreladescripció geomètricadelesimatgespelseumapatopogràfic,ambmoltesaplicacionsala visióperordinador.

Emsentomoltorgullósd’havercol.laboratambVicentCasellesdurantmés devintanys.Hetingutlasortdetreballarambunmatemàticqueposseïa unaculturaiunaformacióexcepcionals.Amés,desdelpuntdevistahumà Vicenteraunapersonaextremamentgenerosa,compartialessevesidees ambqualsevolcompanyqueestiguésinteressateneltema,senselímitsni imposicions.LapetjadahumanaimatemàticadeVicentCasellesserà,entre nosaltresienlacomunitatmatemàticamundial,absolutamentperdurable.

3ContribucionsdeVicentCasellesalainterpolació d’imatges perPabloArias

UndelsinteressosprincipalsdeVicentCasellesalllargdelasevacarrerava serelproblemadelainterpolaciód’imatges.Unaimatgeenescaladegrisos potmodelar-secomunafuncióescalardeﬁnidaenundominirectangular R delplaeuclidià.Suposemqueconeixemelvalord’unaimatgeenunsubconjunt delseudomini D⊂R.Anomenem f : D→ R aquestsvalorsconegutsi O laregiód’interpolació, i.e. O=R\D.Elproblemaés,llavors,trobaruna imatge u : R→ R quecoincideixiamb f a D.Perconcretarelproblemacal donarunanocióprecisadelqueentenemperimatge.Unaimatgeésuna funciómoltcomplexaenlaqualcoexisteixenzonesregulars,discontinuïtats, texturesambpatronscomplexosaleatorisi/ofractals.Unmodelmatemàtic peralainterpolaciód’imatgeshadecapturaraquestsfenòmensisercapaçde reproduir-losambrealisme.Lestècniquesexistentspodenseparar-seenles anomenadesd’inpainting geomètric(olocals)ilestexturals(onolocals).

Elsmètodesd’inpainting geomètricpressuposenalguntipusderegularitat sobrelaimatgeiusenpercompletar-lamecanismesdepropagaciói/odifusió, engeneralmitjançantEDP.Delainformaciódisponiblea D,aquestsmètodes utilitzensolamentaquellaqueestrobaalvoltantde ∂O,d’aquíelterme local. Aquestestècniquesfuncionenbéperaimatgessensetextures(perexemple, regularsatrossos)iperadominisd’interpolaciópetits.

Elsmètodesd’inpainting texturalfuncionencopiantfragmentsdelapart coneguda D a O.Esdiuentambé mètodesperpegats o nolocals (patch-based methods enanglès).Perlasevacapacitatperreproduirtexturessolenobtenirresultatsmoltmésrealistesqueelsdelestècniqueslocals,iaméspoden

aplicar-seadominisd’interpolaciómésgrans.Sónmètodesmésaviatalgorísmicsilasevamodelitzaciómatemàticaésmésdifícil.

Desdeﬁnalsdeladècadadelsnoranta,elsmodelsmatemàticsd’interpolaciód’imatgesvananarevolucionant,aixícomlasevacapacitatdegenerar resultatscadavegadamésrealistesapartirdemenysquantitatdedades.Vicent Casellespotconsiderar-seundelsfundadorsd’aquestcampivacontribuiren granmaneraalseudesenvolupament(tantalainterpolaciógeomètricacoma latextural).

3.1 Inpainting geomètric

ElprimertreballdeCasellessobreeltemaesvapublicarel1998,ambMoreli Sbert[72],is’hiestudiaelproblemad’interpolarunafunciócontínuaapartirde valorsconegutsalafrontera(unacorbadeJordantancada).Elresultatprincipal ésunacaracteritzaciódelsinterpoladorsquecompleixenunasèriederequisits (axiomes)naturals,quecorresponenapropietatsd’invariància(aisometriesi homotècies,iacanvisd’escalaaﬁns)itresaxiomesbàsicssobreladependència ambladadadefrontera:asaber (i) monotoniapelquefaalesdadesdefrontera, (ii) regularitat(dependènciacontínuadeladadaenundominiinﬁnitesimala travésdelessevesderivadesprimeresisegones), (iii) idempotència(si u ésel resultatdel’interpoladora O,i u elresultata O ⊂O usant u comadadade frontera,aleshores u = u|O ).

Suposantquelesdadesdefronterasóncontínues,esdemostraqueels interpoladorsquecompleixenelsaxiomessónsolucionsdeviscositatdel’EDP parabòlicasegüenta O:

G(A) = 0, amb A = uξξ uξη uξη uηη ,

on ξ =∇u/|∇u| éselcampdedireccionsdelgradient, η = ξ⊥ eldelescorbes denivelli G ésunafunciónodecreixenttalque G(aB) = aG(B) pera a ∈ R. Enelcasque G siguidiferenciableal’origen,lesopcionseslimitenencaramés: G(A) = tr(BA) amb B unamatriunonegativa.Aquestresultatmostraqueno hihagairesopcionsperinterpolarraonablement u apartirdelsseusvalorsen lafrontera.Comacasosparticularsdelcas G diferenciable,hihal’estimador harmònic ∆u = 0,el p-laplacià,elmovimentpercurvaturamitjana uηη = 0,iel ∞-laplaciàoAMLE(absolutelyminimizingLipschitzextensions),que corresponaimposarqueladerivadasegonaenladirecciódelgradientsigui nul.la.Aquestúltimpermet,amés,especiﬁcarelvalordelafuncióenpunts aïllats.L’article[72]éslaprimeraaplicaciódel’AMLEalprocessamentd’imatges. EndostreballsposteriorsdeVicentCasellesambMarceloBertalmío,Laura IgualiOliverSanders’esténaquestateoriaaxiomàticaaimatgesdeﬁnidesen superfícies[99,65].

Elsinterpoladorsestudiatsa[72]estanlimitatsennoconèixer-selesderivadesdelafuncióquecalinterpolar.Enlaliteraturasesoldistingirun tipusespecíﬁcdeproblemad’interpolació,enelquallapartconeguda D és

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

unconjuntobertonesconeixenlesderivadesde u.Típicament,eldomini d’interpolació O consisteixenalgunesregions,lafronteradelesqualsésuna corbaregularoregularatrossos.Unexempled’aquesttipusd’interpolacióés quanvolemeditarunaimatgellevant-neunobjecte.Aquestproblemaesconeix perdiversosnoms,elsméscomunssón inpainting, desoclusió, emplenat (ﬁll-in) i eliminaciód’objectes

Elprimerarticled’inpainting geomètricvaserescrittambéel1998,per MasnouiMorel[90].Elsautorsproposeninterpolarlaimatgereconstruintles corbesdenivellinterrompudesper O.Lacorbadenivell λ esdeﬁneixcomla fronteradelconjuntdenivellsuperiora λ,quedenotem Γλ ={x ∈R : u(x) ≥ λ}.Suposantquelescorbesdenivellsónregularsenl’oclusió O,elsautors proposenminimitzarl’energiasegüentperacadacorbadenivell

on s éslalongitudd’arci κ(s) ≥ 0lacurvatura.L’energiatéparàmetres p ≥ 1, α,β> 0.MasnouiMorelpresentenenelseuarticleunalgorismeenginyós percalcularunòptimglobalaplicableúnicamentalcas p = 1.Enaquestcas, l’energiaesredueixalalongituddelacorbaméslavariaciótotaldel’angledel vectortangent,ilescondicionsdevoraadmesessónlesposicionsdelsextrems delacorba.Lacorbaòptimaéssimplementelsegmentderectaqueconnecta totsdosextrems,laqualcosaòbviamentnogaranteixlacontinuïtatdelvector delacorbadenivellalafrontera.Enlaﬁgura1escomparal’AMLEproposata[72]ambl’interpoladordeMasnouiMorel.Mésinteressantéselcas p> 1, enelquall’energiaadmetcomacondicionsdefronteralaposicióiladirecció tangentdelsextremsdelacorba,cosaquepermetestendrecontínuamentel vectortangent.Elcas p = 2corresponal’energiaelàsticad’Euler,usadaper modelarlaﬂexiómecànicadebigues.MasnouiMorelestudienaquestcas,però senseresoldre’lnumèricament.

Figura 1: Comparacióentrel’AMLE[72]il’algorismedeMasnoui Morel[90].ElresultatdeMasnouiMorelpotserdiscontinu.

EltreballdeMasnouiMorelproposaunadescomposiciódelproblema deminimitzarl’energia E(u) endos:lainterpolaciódelescorbesdenivell (morfologiadelaimatge)ilapropagaciódelsnivellsdegrisalllargdelescorbes

denivellinterpolades.Aquestaideaformapartd’unafilosofiapromogudaper Caselles,ColliMorelqueidentificalescorbesdenivell(ilessevessingularitats) comaprimitivesbàsiquesdelesimatges[63].Granpartdeldesenvolupament posteriordelcampsegueixaquestaidea.

L’any2000,Bertalmío,Sapiro,CasellesiBallestervanpublicarelfamós article«Imageinpainting»[36],quevadonarelnomalproblema.Aquesttreball presentaunaEDPevolutivaquebuscaemulareltreballdelsrestauradorsd’art enlarecuperaciódellacunesenpinturesmuralsalfresc. Inpainting éselnom enanglèsqueelsrestauradorsdonenaaquestatasca.L’EDPbuscapropagar una«mesuradelasuavitat»delaimatgealllargdelescorbesdenivelldela imatgebuscada u.Lamesuradesuavitatproposadapelsautorsésellaplacià, laqualcosadonallocaunaEDPdetercerordre: ut =∇⊥u ·∇∆u + ν div(g(|∇u|)∇u).

Elsegonmembredelcostatdretésuntermededifusiónolineal,inclòs permillorarl’estabilitatnumèricadel’EDP.Lanolinealitat g éspositivai decreixent,ambl’objectiudereduirladifusióenzonesdegradientaltpera preservarlesvoresdelsobjectes.Espresentaunadiscretitzaciódel’EDPusant diferènciesfinites,is’obtenenresultatsquealseumomentvanservisualment impressionants(figura2).L’article[36]éselprimerenproposarunaEDPpera inpainting,ivatenirunagraninfluènciaenelstreballsposteriors.Noobstant això,lessevessolucionsmanquendelainterpretabilitatgeomètricadela interpolacióperelàstiquesd’Euler.

Figura 2: Undelsresultatspresentatsa[36].

Apartirdel2001Ballester,Bertalmío,Caselles,SapiroiVerderavanpublicar unasèriedetreballsenelsqualsesproposaminimitzarunarelaxacióde l’energiaelàsticad’Euler[28, 24, 27].Introdueixenuncampvectorial θ : R→ R2 sobreelqualimposenque θ(x) ·∇u(x) =|∇u(x)| i |θ(x)|≤ 1.Ésadir, θ corresponalcampdedireccionsde ∇u.Elsautorsargumentenquesi u ésla funciócaracterísticad’unconjunt Γ llavors R |div (θ)|p|∇u| dx = ∂Γ |κ(s)|p ds.

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

Enfunciód’aquestaobservacióproposenl’energiasegüent: E(u,θ) = R |div (θ)|p(a + b|∇uσ |)dx + ν R (|∇u|− θ ·∇u)dx,

on a,b,ν> 0, p ≥ 1i uσ = u ∗ gσ éslaimatgeconvolucionadaambunnucli gaussià.Elsautorsprovenl’existènciadesolucionsdevariacióﬁtadapera p> 1. Laconstant a ielﬁltratdelaimatgesónnecessarisperalaprova.Lasegona integralforçaqueelcamp θ coincideixiambladirecciódelgradient.Aquest articlevaserelprimeraresoldrenumèricamentl’energiaelàsticad’Eulerper a p> 1(ounarelaxaciód’aquesta).Laintroducciódelcamp θ dedireccionsdel gradienttécomaobjectiuobtenirunaequaciód’Euler-Lagrangeméssimple.Les derivadessegonesde u,necessàriespercalcularlacurvatura,s’expressencom aderivadesdeprimerordrede θ,cosaquedonallocaunaequaciódesegon ordre.Sinoesfesaquestarelaxació,l’EDPresultantseriadequartordre(amés denolineal)i,pertant,moltmésdifícilderesoldrenumèricament.Recentment, altresautorshanproposatalgorismesnumèricsràpidsperal’elàsticad’Euler usantmètodesmodernsd’optimitzacióambrestriccions.Aquestestècniques explotenelmateixprincipid’introduirvariablesauxiliarsutilitzatperCaselles ielsseuscol.laboradorsunsquinzeanysabans.

Entreballsposteriors,aquestatècnicavaserestesapertractarimatges3D[26]ipercompletarforatsensuperfíciestriangulades[103,64].

Figura 3: Notacióperal’inpainting textural,iresultatobtinguta[23].

3.2 Inpainting textural

L’inpainting texturalesvadesenvoluparenparal.lelal’inpainting geomètric.La ideafonamentalvaserproposadaperEfrosiLeungel1999a[77]enelcontext desíntesidetextures.Aquíesbuscaresoldreelproblemasegüent:donadauna imatgeexempled’unatextura,generarunaimatgediferentquesiguipercebuda comsifosdelamateixatextura.EfrosiLeungvanproposarunalgorismemolt simplequevasuperarsigniﬁcativamentelsresultatsobtingutsﬁnsalmoment, entermesdelaqualitatvisualdelestexturesgenerades.Peracadapíxel x de latexturaquecalsintetitzar,se’ntriaunenlatexturad’exempleentreaquells

quetinguinunveísemblatalde x.Elsveïnsusatssónquadrats,perexemple de7per7píxels,iesdiuenpegats(patches enanglès).

Denotaremper pu(x) elpegatde u centraten x,ésadir, pu(x) = u|x+P ,on P éseldominidelpegat:unquadratdecostat s centratenl’origen.Deﬁnirem, amés,elsconjunts O=O+P delscentresdelspegatsqueintersequen O,i D=R\ O eldelspegatsconeguts(ﬁgura3).

Laideadecompararelspegatsperdeﬁnirunamesuradesemblançaentre píxelsvatenirungranimpacteiràpidamentvaseradoptadaperalaresolució demoltsaltresproblemes.EfrosiLeungvanserelsprimersaaplicar-laal problemad’inpainting.Elprimermodelvariacionalqueformalitzavaaquestes ideesvaserproposatcincanysdesprésperDemanet,SongiChana[75]:

E(u,ϕ) = O P (u(x + h) f(ϕ(x) + h))2 dhdx.

Lavariable ϕ ésun mapadecorrespondències ϕ : R→ D queassociaacada posiciódelaimatgeunaposiciósobrelapartconeguda D.S’imposacoma restriccióque ϕ|D = idD.L’energiapenalitzaperacada x ∈ O,lanorma L2 entre pu(x) i pf (ϕ(x)),elpegatconeguta ϕ(x).Demanet,SongiChanrestringeixenlaimatgeinterpolada u aser u(x) = f(ϕ(x)),ésadir, u(x) escalcula copiantelvalorde f enlaposiciócorresponentsegons E(u,ϕ) ésdifícildeminimitzar.Posteriorment,altresautorssuprimeixenlarestricciósobrelaimatge u,ioptimitzenl’energiaalternantminimitzacionsen en ϕ [104, 86].Aquestsenfocamentsconsiderenlesimatgesdiscretitzades, perlaqualcosanopermetenestudiarlaregularitatdelessolucions.

Figura 4: Filasuperior:Resultatsobtingutsa[23]amblesnormes L2 i L1 entrepegatsde u (laimatge),inormes L2 i L1 entreelspegatsde ∇u Filainferior:Resultatsambelmodelquepenalitzalanorma L2 entre pegatsde u

Entreel2009iel2011,CasellesvapublicarambArias,FaccioloiSapirouna sèriedetreballsenelsqualsesproposais’analitzaunafamíliadefuncionals peral’inpainting percòpiadepegats[22, 78, 23].Aqueststreballsestan inspiratsenunalgorismedereducciódesorollpermitjanesnolocalsintroduït

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

perBuades,ColliMorela[41].Apartird’unaimatge f contaminadaambsoroll blancadditiu,s’aproximalaimatgeoriginal u perunamitjanaponderadadels píxelsde f : ˆ u(x) = R w(x,y)f(y)dy.Elpes w(x,y) ponderalacontribució de f(y) alamitjana,iésunafunciódecreixentdeladistància L2 entreels pegatscentratsen x ien y: w(x,y) ≈ exp 1 T pf (x) pf (y) 2 2

GilboaiOsher[82]assenyalenquelesmitjanesnolocalsminimitzenel funcional

E(u) = R R w(x,y)(u(x) f(y))2 dydx.

Enaquestaformulacióelspesos w escalculenapartirdelaimatgesorollosa.En elproblemadel’inpainting aixònoéspossible,jaquenoconeixemelspegats a O.ElmodelproposatperVicentCasellesicoautorsbuscaestimar,juntament amblaimatge,elspesos w : O× D→ R quemesurinlasemblançaentreels pegatssintetitzatsen O ielsconegutsen D:

ET (u,w) = O D w(x,y) pu(x) pf (y) 2 2 dydx TH(w),

amblarestriccióque w(x, ·) sumi1sobre D.Elterme H(w) mesural’entropia delspesos w.Perminimitzarl’energias’alternenminimitzacionsen u ien w Amésd’introduirelterme entropia al’equacióanterior,unaaltramodiﬁcació pelquefaalfuncionaldeGilboaiOsherésquelesdiferènciesentrepíxels sesubstitueixenperladistància L2 entrepegats.Aixòtécomaconseqüència queenminimitzarrespectede u,mantenintﬁxoselspesos w,esrealitzi unamitjananolocaldepegatssencersenllocdepíxels.Enminimitzaren w s’obtenenpesoscomelsusatsperBuades,ColliMorel.Elparàmetre T controla laselectivitatd’aquestspesos.Si T →∞, w(x, ·) tendeixaunadistribució uniformesobre D,ienminimitzaren u ompliremcada u(x) comunamitjana detota D.Si T → 0elspesosconcentrenlasevamassaenelspegatsde D més propersalpegata x.Aquestéselcasrellevantperalproblemad’inpainting,en elqualesbuscacopiartrossosdelapartconegudadelaimatgesensefer-nela mitjana.

Usantaltresdistànciesentrepegatsespodendeﬁnirdiversosfuncionalsque donenllocaalgorismesd’inpainting ambdeterminadespropietats.Elsautors considerenlanorma L1,lanormalitzaciódelaqualpelquefaa u donalloca unamitjananolocalponderada,inormes L2 i L1 entrepegatsdelesimatges degradients ∇u i ∇f .Aquestsmodelspermetencopiara O gradientsde f ques’integrenperobtenir u,resolentunaEDPa O ambcondicionsdeDirichlet u(x) = f(x) a ∂O.Enlaﬁgura4escomparenelsresultatsobtingutsamb diferentsmodels.Enlaimatgehihaunsofàquetravessaunatransiciógradual d’il.luminació.Elsmètodesquecopienpegatsde u propaguenelsextrems clarifoscigenerenunatransicióabrupta,mentrequeelsmètodesbasatsen gradientsaconsegueixenunatransicióregular.

A[21]s’estudienelsfuncionalsproposats(ambl’excepciódelqueusala norma L1 delgradient)pera T> 0,iesproval’existènciadesolucionsregularsi

laconvergènciadel’algorismedeminimitzaciócapaunpuntcrític.Quan T → 0, elsautorsdemostrenqueelsfuncionals,basatsennormes L2, Γ -convergeixen aunaenergiasimilaraladeDemanet,SongiChan,enaquestesnormesels pesos w convergeixenaunmapadecorrespondències ϕ,iestableixenun vincleentreelsmodelsnolocalsd’inpainting ielsdereducciódesoroll.Sobre el Γ -límit T = 0provenquehihasolucionsambmapesdecorrespondències ϕ quesónlímituniformedefuncionsdevariacióﬁtada,encaraqueassenyalen queenelsexperimentsmoltesvegadess’obtenenmapes ϕ quesóntranslacions atrossos,laqualcosasuggereixquelaregularitatde ϕ podriasermésforta.

3.3Extensionsaimatgesdeﬁnidesenvarietats

Enelsúltimsanys,Casellesesvainteressarperestendrealgunsmodelsd’interpolacióidifusióaimatgesdefinidessobrevarietatsriemannianes.Lamotivació éslad’obteniroperadorsanisotròpicsperaunaimatgedotant-lad’unamètricaqueentinguiencomptelageometria.A[42]esproposaunenfocament axiomàticperdefinirespaisd’escalesd’imatgesdefinidessobrevarietatsriemannianes.Elresultatésunasèried’EDPquegenerenespaisd’escalesanisotròpiques.A[25]s’estudiaelproblemadecompararpegatsdeduesimatges ambmètriquesriemannianesdiferents,aplicantl’enfocamentaxiomàticala funciódesemblançaentreveïnsdelesduesimatges.Elcaslineals’estudia enmésdetalla[80],onamésesmostracomespotusaraquestformalisme perdefinircriterisdesemblancesinvariantsafins.Aquestscriterisvanser usatsdesprésperproposarunalgorismed’inpainting quepotcopiarpegats modificatsmitjançantunatransformacióafí[79].

4L’aportaciódeVicentCasellesalproblemadeladetecció decontornsenunaimatgedigitalapartirdelescorbes geodèsiques perBartomeuColl

Undelsproblemesclàssicsenelprocessamentd’imatgeséselproblemade ladetecciódecontornso,equivalentment,trobarlescorbesofronteresque separenregionshomogèniesd’unaimatge.Aquestvaserundelsprimers problemesenquèVicentCasellesvatreballarenelcampdelprocessament d’imatgesapartird’unaformulacióclàssicadelproblemaproposadacomuna minimitzaciód’undeterminatfuncionald’energiaperKass etal. [85].Enuna primeraaproximació,Casellesvavolerentendreicomprendrebéelmodel d’energiapersabercomhopodiainterpretarapartirdelateoriad’evolució decorbesiﬂuxosgeomètrics.Enunprimertreballconjunt[61],Caselles etal. proposenunmodeldonatperunﬂuxqueevolucionasegonsunaEDP,basat enelmovimentdelacurvaturamitjana,elqualpermetcanvisautomàticsen latopologiadel’objecte,amésdepoderdetectarsimultàniamentisensecap coneixementprevidiversosobjectesdelaimatge.Posteriorment,enunsegon treballconjuntambKimmeliSapir[66],provenqueelmodelclàssicd’energia

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

ésequivalentatrobarunacorbageodèsicaenunespaideRiemannambuna mètricaqueesderivadelamateixaimatge.Aixòsigniﬁcaque,enundeterminat marc,ladetecciód’unafronterapotserconsideradaequivalentalcàlculd’una corbadelongitudmínimaponderada.Aquesttreballvamarcarunaﬁtaenel problemadeladeteccióosegmentaciód’objectesenunaimatge,ivaserun delsméscitatsenaquestaàrea.

4.1ElmodelgeodèsicdecontornsactiusdeCaselles,KimmeliSapiro L’aproximacióclàssicaalproblemaproposadaperKass etal. a[85],anomenada de contornsactius (o snakes enanglès)perlaformadel’evoluciódelescorbes, estàbasadaenladeformaciód’uncontorninicial C0 capalafronterade l’objectequeesvoldetectar.Aquestscontornsactiussónexemplesdetècniques demodelsdedeformaciód’objectesbasatsenlaminimitzaciód’unaenergia; vegeu[38,102].

Elfuncionald’energiarelacionatamblacorbaplana C queactuasobrela imatge I vedonatper

on α, β i λ sónconstantsrealspositives.Elsdosprimerstermescontrolenla regularitatdelscontornsques’handedetectar(energiainterna),mentrequeel tercertermeéselresponsabled’atreureelcontorncapal’objectedelaimatge (energiaexterna).

EneltreballdeCaselles etal. [66]elsautorss’adonenqueaquestaformulaciótambéfuncionaamb β = 0ienaquestcasespotestendrealapart dedetecciódecontornssiagafemunafunció g : [0, +∞) → R+ estrictament decreixenttalque g(r) → 0quan r →∞.Pertant, −|∇I| espotsubstituir per g(|∇I|)2 is’obtéunaenergiamésgeneral,donadapelfuncionalsegüent

Amés,elfuncional (17) noésintrínsec,jaquedepèndelaparametrització q, laqualésarbitrària.Peròpodemdeﬁnirunanovaparametrització q = φ(r), φ : [c,d] → [0, 1], φ > 0,laqualcosapermettrobarunasolucióescollintuna parametritzacióquesíqueésintrínsecaalacorba.

ElpassegüentdeltreballdeCaselles etal. [66]ésprovarquelasolucióen laminimitzaciódel’energiadelmodel (17) vedonadaperunacorbageodèsica enl’espaideRiemanninduïtperlamateixaimatge I.Recordemqueuna corbageodèsicaésuncamídedistànciamínima(local)entrepuntsdonats. Llavors,perprovarquelasolucióésunacorbageodèsicaenl’espaideRiemann, Caselles etal. usenelprincipiclàssicdeMaupertuisperasistemesdinàmics (Dubrovin etal. [76]).Aquestprincipiensdonalasoluciódelproblemade l’energiaenlaformad’unacorbademínimadistànciaponderadaentrepunts donats.

Ambtotaixò,Caselles etal. [66]provenqueelproblemademinimitzar (17) estransformaenunproblemadecalcularunageodèsicaenunespaideRiemann,segonsunanovamètrica,elqualésequivalentatrobar

Perresoldre (18),unamaneradefer-hoésemprarelmètodedeldescensdel gradientenlasevaversióràpida,apartirdel’equaciód’Euler-Lagrangede (18). Llavorsladeformaciódelacorbainicial C(0) = C0 capaunmínim(local)del funcional(18)hadeseguirl’equaciód’evolució

on κ éslacurvaturaeuclidianai N éselvectornormalalacorbaqueapunta capal’interiorde C.

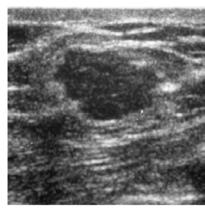
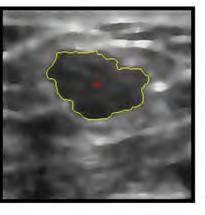
Figura 5: Enaquestexemple,l’algorismedeCaselles etal. enspermet ladeteccióautomàticadelsnòdulsdemama.

4.2Interpretaciódelﬂuxgeodèsicapartirdelsconjuntsdenivell

Lainterpretaciódel’equació (19) passaperl’aproximaciódelsconjuntsde nivell(vegeuOsheriSethian[92,101]),talcomesdescriuseguidament. Suposemquelacorba C ésunconjuntdenivelldelafunció u : [0,a] × [0,b] → R i,pertant, u donaunarepresentacióimplícitadelacorba C.Aquesta representacióésintrínseca(nodepèndeparàmetres)itambétélapropietat quetopologiesdiferentsdelconjuntdenivellzeronoimpliquentopologies diferentsde u.Ésfàcilveurequesilacorbaplana C evolucionasegonsl’equació Ct = βN peraunacertafunció β,llavorslafunció u esdeformad’acord ambl’equació ut = β|∇u|,on β escalculasobreelsconjuntsdenivell.

Basant-nosenl’expressió (18) iinserintl’evolucióde C enl’equació (19) dinsde u,obtenimqueresoldreelproblemageodèsicésequivalentacercar

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

lasolució u del’estatasimptòtic, ∂u(t) ∂t = 0,del’equaciód’evoluciósegüent, ambcondicióinicial u(0,C) = u0(C),

=|∇u| div g(I) ∇u |∇u| =

g(I)|∇u|κ +∇g(I) ·∇u. (20)

Elterme g(I)|∇u|κ+∇g(I)·∇u ésl’equaciód’Euler-Lagrangedelfuncional (18) amblacorba C representadapelconjuntdenivellde u ilacurvatura κ calculada sobreelsconjuntsdenivellde u.

Figura 6: Exempledel’aplicaciódelmodelgeodèsicdeCaselles,Kimmel iSapiro,enladetecciód’unalesiócutània.

4.3Ladetecciódelafronteraapartirdel’evoluciódelsconjuntsde nivell

Enelseuprimertreballdinselcampdelesimatges,VicentCasellesvaproposar unaequacióbasadaenelmovimentdelacurvaturamitjanasobrelescorbes denivelld’unafunció u peraladetecciódelscontorns.Enaquesttreball, Caselles etal. [61]proposenelmodeld’EDPsegüentperadetectarlafrontera d’unobjecte O ut = g(I)|∇u| div ∇u |∇u| + ν = = g(I)(κ + ν)|∇u|, (21) on ν ésunaconstantpositivareali g(I) éslafuncióqueatural’evolucióde lacorbaquanarribaalafronteradel’objecte.Uncasparticularseriaagafar g(I) = 1 1+|∇I|p ,on ˆ I ésunaversióregularitzadade I,perexemple,laconvolució amblagaussiana,i p = 1, 2.Aquestmodeld’evoluciótambévaserproposat perMalladi etal. [88,89]alamateixaèpoca.

Lainterpretaciógeomètricaqueespotferdel’equació (21) éslasegüent.El ﬂux ut = (κ + ν)|∇u|

descriudequinamaneracadaundelsconjuntsdenivell C de u evoluciona segonsl’equació

Ct = (κ + ν)N ,

on N=− ∇u |∇u| éselvectornormalalacorbaqueapuntacapal’interiorde C. AquestaequacióvaserproposadaperprimeravegadaperOsheriSethian[92, 101],onesfeiaunestudicompletsobrel’anàlisinumèricadel’equació.Noteu quequanlacurvaturas’anul.la(perexemple,quanpassemperlafronterad’un objectelaconvexitatdelqualcanvia),elterme νN actuacomunavelocitat constanti,pertant,lacorbasegueixlasevaevolució.Enaquestcas,elterme develocitatconstantempenylacorbacapendins(ocapafora)iéscrucialen elmodel (21) perpermetrecapturarformesnoconvexesapartirdecorbes inicialsconvexes.

Enelcasparticular ν = 0,l’equaciód’evoluciódecadaundelsconjuntsde nivell C de u vedonadaper

Ct = κN , anomenadaequaciódel fluxeuclidiàdelacalor (Euclidianheatflow),coneguda perlessevespropietatsgeomètriquesderegularització.Elfluxfadecréixer lacurvaturatotal,aixícomtambéelnombredezerosdelasegonaderivada (zero-crossings)ielsvalorscríticsdelacurvatura(màximsimínims).La«força» donadaperlacurvatura κ actuacomlaforçainternaenelmodelclàssic (16), mentrequeelfluxeuclidiàdelacalor Ct = κN ésexactamentelfluxde regularitzaciódelacurvaturaquereemplaçaeltermederegularitzaciód’ordre méselevatenelmateixmodel(16).

Sicomparemelsmodelsdonatsperlesequacions (20) i (21),ensadonemde ladesapariciódelterme ∇g(I) ·∇u enlaprimeraformulaciódelmodel (21). Aquesttermeatreulacorbacapalesfronteresdelsobjectes(∇g apuntacapa lameitatdelafrontera),amésdepermetreladetecciód’objectesnoconvexos. Noteuqueenelprimermodellacorbas’aturaquan g = 0iaquestfetnoméses donaencontornsideals(quanestéunafrontera«nítida»ambungradientde valoraltconstant),mentreque,enelcasgeodèsic,elterme ∇g(I) ·∇u és degranajudaquanlafronteradel’objectetévariacionsaltessobreelsvalors delgradient.Unaltreavantatged’aquestnoutermeésquepodemeliminar parcialmentlanecessitatdelavelocitatconstantdonadaper ν enelmodel (21) perdetectarobjectesnoconvexos,jaqueintrodueixunparàmetreextra.

Enelcasqueesvulguiafegiralmodelgeodèsicaquestaforçaconstantde caraaincrementar,perexemple,lavelocitatdeconvergència,podemconsiderar elterme νg(I)|∇u| comunlligamd’àreaenelproblemageodèsic (18),on ν éselmultiplicadordeLagrange.Enaquestcass’obtél’equació

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

obélasevaversióapartirdelmovimentdelsconjuntsdenivell

Ct = g(I)(ν + κ)N− (∇g(I) N )N , (23)

anomenadapelsautorsdeltreball[66] modelgeneraldelscontornsactius geodèsics.

Figura 7: Exempledel’aplicaciódel’algorismedeCaselles etal. on lacondicióinicialésinterioral’objecte(ﬁgurasuperior)oexteriora l’objecte(ﬁgurainferior).

Basant-seenlateoriadesolucionsdeviscositat[73],Caselles,Kimmeli Sapiroprovenelteoremasegüentd’existènciaiunicitatdesolucióperalmodel generalgeodèsic (22).Enl’enunciat, BUC(R2) denotaelconjuntdelesfuncions uniformementcontínuesacotadessobre R2

Teorema 1. Sigui W 1,∞ l’espaidelesfuncionsLipschitzﬁtadesen R2.Suposem que g ≥ 0 ésunafunciótalque supx∈R2 |Dg1/2(x)| < ∞ i supx∈R2 |D2g(x)| < ∞.

Sigui u0 ∈ BUC(R2) ∩ W 1,∞(R2).Aleshores

(1)L’equació (22),admetunaúnicasoluciódeviscositat

u ∈ C([0, ∞) × R2) ∩ L∞(0,T ; W 1,∞(R2)

peratot T< ∞.Améssatisfà

inf u0 ≤ u(t,x) ≤||u0 v0||∞.

(2) Sigui v ∈ C([0, ∞) × R2) lasoluciódeviscositatde (22) corresponentala condicióinicial v0 ∈ C(R2) ∩ W 1,∞(R2).Llavors

||u(t,.) v(t,.)||∞ ≤||u0 v0||∞

peratot t ≥ 0.Aquestfetprovaquel’únicasolucióésestable.

4.4ExtensiódelmodelCaselles-Kimmel-Sapiroalcasdeladetecció d’objectes3D

Basant-seeneltreball[67],Caselles etal. estenenelresultatdelscontorns actiusgeodèsicsalcas3Dapartirdelaconstrucciód’unmodeldesuperfícies deformablesqueesmouencapalsobjectes3Dqueesvolendetectar.Aquesta deformacióésobtingudaapartirdelaminimitzaciód’unfuncionaldetal maneraqueelseumínimlocals’agaﬁalafronteradel’objecte;vegeu[102, 38]. EnelstreballsdeCasellesencol.laboracióambKimmel,SapiroiSbert[68, 67], elmodel3Dproposatesbasaenelmovimentdelacurvaturaielcàlcul delessuperfíciesambàreamínima,conegudescomasuperfíciesminimals. Aixòsigniﬁcaquedetectarl’objecteésequivalentatrobarunasuperfícied’àrea ponderadaminimal,onelpesvedonatperlamateixaimatge.Mésconcretament iextrapolantlaideadelcas2D,estractademinimitzar l’àreaponderada

AR = g(I)da,

on da ésl’elementd’àreai g(I) ésunafunciópes,positivaidecreixent,igual queperalcasd’unaimatge.

Figura 8: Esquerra:Exempled’aplicaciódel’algorismeenladetecció3D basaten[67, 68]dedostorusenganxats.Dreta:Exempledel’evolució capaladetecciód’untumorenunaimatgeMRI.

L’equaciód’Euler-Lagrangede AR donallocalﬂux

∂S

∂t = (gH−∇g∇· N )N ,

on S éslasuperfície3D, N éselvectornormalunitarialasuperfíciequeapunta al’interiori H ésigualaduesvegadeslacurvaturamitjanade S.Delamateixa maneraqueenelcas2D,s’obtéunaequaciód’evolucióperalconjuntdenivell k, u = k,onlasuperfícied’evolucióestàdeﬁnidaper S(t) ={x : u(t,x) = 0},la qualésestable,robustaipermettambécanvisdelatopologiadelasuperfície durantelprocésdedeformació.

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

5SobrelacontribuciódeVicentCasellesalprocessament d’imatgesencolordemodelsvariacionalsinspirat enlavisióhumana

perEdoardoProvenzi

5.1Introduccióalcolor

El1997,CasellesiSapirovanutilitzarprincipisvariacionalsperferunainterpretaciónovadel’equalitzacióperhistogramad’unaimatgedigital.Elseu treball,profundid’unmèritindiscutible,vaserutilitzatunadècadaméstard perconstruirunmarcvariacionalperalrealçamentdelcolorinspiratenles propietatsdelsistemadevisióhumà.Acontinuacióendescriuremelsresultats corresponents.

5.2ElfuncionaldeCaselles-Sapiroperal’equalitzaciód’histograma

Fixemlanotació.Sigui Ω ⊂ Z2 el dominiespacial d’unaimatgedigital, |Ω| és elnombredepíxelsdelaimatge,lescoordenadesespacialsdelaqualseran denotadesper x ≡ (x1,x2) i y ≡ (y1,y2).Sempreconsideraremun rang dinàmicnormalitzat a [0, 1],demaneraqueuna funciód’imatgeRGB serà denotadaper I : Ω → [0, 1] × [0, 1] × [0, 1], x (IR(x),IG(x),IB (x)),oncada componentescalardeﬁneixelnivelld’intensitatdelpíxel x ∈ Ω enelcanal vermell,verdiblau,respectivament.Noésimportantespeciﬁcaruncanalde colorparticular,aixíquedenotaremqualsevoldelscomponentsescalarsdela imatgesenzillamentper I(x)

Recordembreumentquèésl’equalitzaciód’histograma.Sigui λ ∈ [0, 1] un nivelld’intensitatgenèric,llavorsl’histogramanormalitzat de I calculata λ és:

h(λ) = 1 |Ω| card{x ∈ Ω | I(x) = λ},λ ∈ [0, 1], (24)

i.e. la probabilitatdetrobarunpíxelambintensitatiguala λ; card éselcardinal delconjuntentreclaus.

L’histogramaacumulatiu de I calculata λ, H(λ),és:

H(λ) = 1 |Ω| card{x ∈ Ω | I(x) ≤ λ},λ ∈ [0, 1], (25)

i.e. la probabilitatdetrobarunpíxelambintensitatmenoroigualque λ.

Esdiuqueunaimatgeés equalitzada si cadanivelltélamateixaprobabilitat d’aparèixer, i.e. si h(λ) ≡ 1,peratot λ,quenaturalmentpotsertraduïtala condiciósegüental’histogramaacumulatiu: H(λ) = λ,peratot λ.

Ésfàcildeprovar(vegeu, e.g. [83])quelatransformacióde [0, 1] ensimateix donadaper λ → H(λ) ésl’aplicacióméssimplequeimplemental’equalització del’histograma.

VicentCasellesiGuillermoSapiroenelseuarticle[100]vanferunainterpretacióvariacionaldel’equalitzaciódel’histograma.Elsseusresultatsespoden

resumirdelamanerasegüent.Donatunfuncional Ehisteq(I) ≡ 2 x∈Ω I(x) 1 2 2 1 |Ω| x∈Ω y∈Ω |I(x) I(y)|, (26)

si I∗ = argminI Ehisteq(I),aleshores I∗ téhistogramaequalitzat, i.e. H(I∗(x)) = I∗(x) peratot x ∈ Ω

Amés,si I0 éslaimatgeoriginal,llavorselproblemadevalorinicialperal descensdelgradient

∂t I =−δEhisteq(I), I(0) = I0, ténomésunasolució,on t éselparàmetred’evoluciódel’esquemadedescens delgradientiteratiui δ representalaprimeravariaciódelfuncional. Ehisteq(I) s’anomenarà funcionaldeCaselles-Sapiro d’araenendavant.

Lainterpretaciódel’energiafuncional Ehisteq(I) entermesdelescaracterístiquesdelaimatgeéscrucial.Primerdetot,femnotarquepodemescriure

Ehisteq(I) = D 1 2 (I) C(I), on

D 1 2 (I) = 2 x∈Ω I(x) 1 2 2 i C(I) = 1 |Ω| x∈Ω y∈Ω |I(x) I(y)|.

Pertant,laminimitzacióde Ehisteq(I) = D 1 2 (I) C(I) s’assoleixatravésdela minimitzacióde D(I) ila maximitzacióde C(I) (degutalsignemenysdavant d’aquestaquantitat).

Elsigniﬁcatdelsdostermesfuncionalséselsegüent:

• D 1 2 (I) s’anomena termededispersióquadràticaglobal alvoltantdelnivell degrismitjà1/2iesminimitzaquan I(x) ≡ 1/2peratot x ∈ Ω, i.e. la minimitzaciód’aquesttermetendeixaconvertir I enunaimatgeuniforme engris;

• C(I) s’anomena termedecontrastglobal ilasevamaximitzacióampliﬁca elcontrastglobaldelaimatge I,expressadapelconjuntdediferènciesen valorabsolut |I(x) I(y)|.

Així,l’argumentminimitzadordelfuncionaldeCaselles-Sapiroéslaimatgeque corresponal’equilibriòptimentre dosefectesoposats:perunabanda,laminimitzacióde D 1 2 (I) tendeixa ﬁxartotselsnivellsalgrismitjà 1/2però,del’altra banda,laminimitzacióde C(I) tendeixa separarelsnivellsd’intensitatl’unde l’altre,tantcomsiguipossible.L’equilibrientrelesduesaccionscontraposades indueixal’equalitzaciódel’histograma.

Unaconseqüènciapràcticad’aquestresultatésque,aplicantperexemple latècnicadedescensdelgradientperminimitzar Ehisteq(I),hompotpararel procésdeminimitzacióabansd’assolirl’equalitzaciócompleta,iaconseguir pertantuna equalitzacióparcial que,noobstantaixò,potserútilperevitar elrealçamentexcessiutípicd’imatgessubexposades(vegeu[83]peramés detalls).

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

Tanmateix,peralspropòsitsdeprocessamentdelcolordelaimatge,les conseqüènciesmésimportantsd’aquestresultatsónteòriques:defet,tal comveuremenlaproperasecció,podemmodiﬁcarelfuncional Ehisteq(I) detalmaneraqueelprincipid’equilibribàsicdel’equalitzaciódel’histogramaesconserva,peròpodemcanviarlaformaanalíticadelstermes D 1 2 (I) i C(I) inspirant-nosenlescaracterístiquesdepercepciódelavisióhumana.La imatge I∗ minimitzadoradelfuncionalmodiﬁcatésunaversiócorrectorade colordelaimatgeoriginalguiadaperlespropietatsdepercepciódelsistema visualhumà.

5.3ModiﬁcaciódelfuncionaldeCasellesiSapiroambcaracterístiques depercepcióhumana

L’enllaçentrelainterpretacióvariacionaldel’equalitzaciódel’histogramai lespropietatsdelsistemavisualhumàrauenelfetquetambélapercepció visualescaracteritzaperl’equilibrientreduesaccionsoposades,peròamb algunesdiferènciesimportants.Acontinuació,veuremaquestessemblancesi diferències.

Primerdetot,quanenstrobemimmersosenunaescenavisual,lanostra visiós’adaptaperpercebremodulacionsalvoltantdelaluminànciamitjanade l’escena,unapropietatanomenada adaptacióvisual,quepotserconsiderada l’anàlogadel’acciódeltermededispersió.

Llavors,persegmentarmillorl’objecte,elnostresistemavisualintensiﬁca elcontrastd’unamaneraquedepèndel’espai.Enelsentitdelesimatges,el canvidecontrastpotserdegutal’aplicaciód’unoperadorglobalqueactuï sobretotalaimatgeobéqueelcanvidecontrastsiguilocal(operadorlocal queactuaenunentorndecadapunt).

Finalment,hihaduescaracterístiquesparticularsquenosónconsiderades dinsdel’histogramad’equalització:laconstànciadelcolorilalleideWeberFechner.Laprimerapropietatesrefereixal’habilitatdepercebreelsmateixos colorssotail.luminantsdiferents,mentrequeelsegonpotsermésomenys descritcomlarespostalogarítmicadelavistahumanaacanvisd’intensitatde lallum.

A[93],esvademostrarque,pertaldetenirencompteaquestespropietats, eltermedecontrast C(I) del’energia Ehisteq(I) s’hademodiﬁcardelamanera següent:

C ϕ w (I) = x∈Ω y∈Ω w( x y )ϕ min(I(x),I(y)) max(I(x),I(y)) , on w ésunafunciódecreixentdeladistància x y entrepíxels,cosaque donallocaltermedecontrast,i ϕ ésunafunciódiferenciablemonòtona creixent,elsigniﬁcatdelaqualdiscutiremméstard.

Elquocient min(I(x),I(y))/ max(I(x),I(y)) ésinvariantrespectedelscanvisd’il.luminaciódeltipus I(x) λI(x),on λ> 0ésl’efected’unil.luminant uniformenoneutre.Pertant, C ϕ w (I) estàenlalíniadelaconstànciadecolor,i

espotdemostrartambé(vegeu[93]unaltrecop)queaquestaformade C ϕ w (I) éscoherentamblalleideWeber-Fechner.

C ϕ w (I) ésnodiferenciableperlapresènciaamagadadelvalorabsolutenles expressions min i max,peròespotregularitzar,demaneraqueeltermedel contrastregularitzatsiguidiferenciable.Vegeu[93]peramésdetalls.Aquesta primeravariació δC ϕ w (I) éssempreunafuncióde1/I(x),iaixòimplicaque, siesvolmantenirlacoherènciadimensional,noespotutilitzarméselterme quadràticdedispersió.Untermededispersiócoherentambladimensióve donatperl’entropia:

α,β(I) = α x∈Ω µ log µ I(x) (µ I(x)) + + β x∈Ω I0(x) log I0(x)

Aleshores,l’energiaglobalqueadaptaelfuncionaldeCaselles-Sapiroales propietatsdelavisióhumanaés Eϕ w,α,β = Dα,β(I) + C ϕ w (I). A[93]esvademostrarque,sotaunescondicionsadequadespera α i β, unesquemadedescensdelgradientsemiimplícitpera log I,inicialitzatamb laimatgeoriginal,convergeixal’únicaimatgequeéspuntﬁxde Eϕ w,α,β.Una anàlisidetalladad’aquestalgorismeestrobaa[81].Alaﬁgura9esveuen resultatsd’aquestalgorisme.

Figura 9: Esquerra:Imatgesoriginals.Dreta:Resultatdel’algorisme variacionalamb ϕ = id iunaeleccióadequadadeparàmetres.Notemel realçamentdelcontrastilareducciódelrepartimentdelcolor.

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

Desd’unpuntdevistateòric,ésinteressantremarcarque,sitriem ϕ = id, lafuncióidentitat,aleshoresl’algorismevariacionalcorresponentésunaversió simètricacontínuadel’algorismeoriginalRetinex[87, 95, 34],mentreque siposem ϕ = log,aleshoresobtenimunaversióvariacionaldel’anomenat algorismed’ACE [96,35].

Finalment,caldirqueelmarcvariacionalqueacabemdediscutirvainspirar unaformulacióbasadaenondetes[94]iunainvestigaciómésgeneralde fenòmensperceptualsicognitiusquedepenendelcontext[84].

Referències

[1] Almgren,F.;Taylor,J.E.;Wang,L. «Curvature-drivenﬂows:avariationalapproach». SIAMJ.ControlOptim.,31(2)(1993),387–438.

[2] Alter,F.;Caselles,V. «UniquenessoftheCheegersetofaconvexbody». NonlinearAnal.,70(1)(2009),32–44.

[3] Alter,F.;Caselles,V.;Chambolle,A. «Acharacterizationofconvex calibrablesetsin RN ». Math.Ann.,332(2)(2005),329–366.

[4] Ambrosio,L.;Caselles,V.;Masnou,S.;Morel,J.-M. «Connectedcomponentsofsetsofﬁniteperimeterandapplicationstoimageprocessing». J.Eur.Math.Soc.(JEMS),3(1)(2001),39–92.

[5] Andreu,F.;Ballester,C.;Caselles,V.;Mazón,J.M. «Minimizingtotal variationﬂow». DiﬀerentialIntegralEquations,14(3)(2001),321–360.

[6] Andreu,F.;Caselles,V.;Díaz,J.I.;Mazón,J.M. «Somequalitative propertiesforthetotalvariationﬂow». J.Funct.Anal.,188(2)(2002), 516–547.

[7] Andreu,F.;Caselles,V.;Martínez,J.;Mazón,J.M. «Theessential spectrumofAM-compactoperators». Indag.Math.(N.S.),2(2)(1991), 149–158.

[8] Andreu-Vaillo,F.;Caselles,V.;Mazón,J.M. «Existenceanduniquenessofasolutionforaparabolicquasilinearproblemforlineargrowth functionalswith L1 data». Math.Ann.,322(1)(2002),139–206.

[9] Andreu,F.;Caselles,V.;Mazón,J.M. «Aparabolicquasilinearproblem forlineargrowthfunctionals». Rev.Mat.Iberoamericana,18(1)(2002), 135–185.

[10] Andreu-Vaillo,F.;Caselles,V.;Mazón,J.M. ParabolicQuasilinear EquationsMinimizingLinearGrowthFunctionals.Basilea:Birkhäuser Verlag,2004.(ProgressinMathematics;223)

[11] Andreu,F.;Caselles,V.;Mazón,J.M. «Astronglydegeneratequasilinear equation:theellipticcase». Ann.Sc.Norm.Super.PisaCl.Sci.(5),3(3) (2004),555–587.

[12] Andreu,F.;Caselles,V.;Mazón,J.M. «TheCauchyproblemfora stronglydegeneratequasilinearequation». J.Eur.Math.Soc.(JEMS),7(3) (2005),361–393.

[13] Andreu,F.;Caselles,V.;Mazón,J.M. «Astronglydegeneratequasilinear equation:theparaboliccase». Arch.Ration.Mech.Anal.,176(3)(2005), 415–453.

[14] Andreu,F.;Caselles,V.;Mazón,J.M. «Someregularityresultsonthe ‘relativistic’heatequation». J.DiﬀerentialEquations,245(12)(2008), 3639–3663.

[15] Andreu,F.;Caselles,V.;Mazón,J.M. «AFisher-Kolmogorovequation withﬁnitespeedofpropagation». J.DiﬀerentialEquations,248(10) (2010),2528–2561.

[16] Andreu,F.;Caselles,V.;Mazón,J.M.;Moll,S. «Finitepropagation speedforlimitedﬂuxdiﬀusionequations». Arch.Ration.Mech.Anal., 182(2)(2006),269–297.

[17] Andreu,F.;Caselles,V.;Mazón,J.M.;Moll,S. «TheDirichletproblem associatedtotherelativisticheatequation». Math.Ann.,347(1)(2010), 135–199.

[18] Andreu,F.;Caselles,V.;Mazón,J.M.;Soler,J.;Verbeni,M. «Radially symmetricsolutionsofatempereddiﬀusionequation.Aporousmedia, ﬂux-limitedcase». SIAMJ.Math.Anal.,44(2)(2012),1019–1049.

[19] Aràndiga,F.;Caselles,V. «Approximationsofpositiveoperatorsand continuityofthespectralradius». J.OperatorTheory,26(1)(1991), 53–71.

[20] Aràndiga,F.;Caselles,V. «Approximationsofpositiveoperatorsand continuityofthespectralradiusII». Math.Z.,209(4)(1992),547–558.

[21] Arias,P.;Caselles,V.;Facciolo,G. «Analysisofavariationalframework forexemplar-basedimageinpainting». MultiscaleModel.Simul.,10(2) (2012),473–514.

[22] Arias,P.;Caselles,V.;Sapiro,G. «Avariationalframeworkfornon-local imageinpainting».A: EnergyMinimizationMethodsinComputerVision andPatternRecognition.Berlín;Heidelberg:Springer,2009,345–358. (LectureNotesinComputerScience;5681)

[23] Arias,P.;Facciolo,G.;Caselles,V.;Sapiro,G. «Avariationalframework forexemplar-basedimageinpainting». Int.J.Comput.Vis.,93(3)(2011), 319–347.

[24] Ballester,C.;Bertalmio,M.;Caselles,V.;Sapiro,G.;Verdera,J. «Filling-inbyjointinterpolationofvectorﬁeldsandgraylevels». IEEE Trans.ImageProcess.,10(8)(2001),1200–1211.

[25] Ballester,C.;Calderero,F.;Caselles,V.;Facciolo,G. «MultiscaleanalysisofsimilaritiesbetweenimagesonRiemannianmanifolds». MultiscaleModel.Simul.,12(2)(2014),616–649.

[26] Ballester,C.;Caselles,V.;Verdera,J. «Avariationalmodelfordisocclusion».A: Proceedings2003InternationalConferenceonImageProcessing.Vol.2.Piscataway,NJ:IEEESignalProcessingSociety,2003,III–677–80.

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

[27] Ballester,C.;Caselles,V.;Verdera,J. «Disocclusionbyjointinterpolationofvectorﬁeldsandgraylevels». MultiscaleModel.Simul.,2(1) (2003),80–123.

[28] Ballester,C.;Caselles,V.;Verdera,J.;Bertalmio,M.;Sapiro,G. «Avariationalmodelforﬁlling-ingraylevelandcolorimages».A: ProceedingsEighthIEEEInternationalConferenceonComputerVision.ICCV 2001.Vol.1.Piscataway,NJ:IEEESignalProcessingSociety,2001,10–16.

[29] Bellettini,G.;Caselles,V.;Chambolle,A.;Novaga,M. «Crystalline meancurvatureﬂowofconvexsets». Arch.Ration.Mech.Anal.,179(1) (2006),109–152.

[30] Bellettini,G.;Caselles,V.;Chambolle,A.;Novaga,M. «Thevolume preservingcrystallinemeancurvatureﬂowofconvexsetsin RN ». J.Math. PuresAppl.(9),92(5)(2009),499–527.

[31] Bellettini,G.;Caselles,V.;Novaga,M. «Thetotalvariationﬂowin Rn». DiﬀerentialEquations,184(2)(2002),475–525.

[32] Bellettini,G.;Caselles,V.;Novaga,M. «Explicitsolutionsoftheeigenvalueproblem div Du |Du| = u in R2». SIAMJ.Math.Anal.,36(4)(2005), 1095–1129.

[33] Bernot,M.;Caselles,V.;Morel,J.-M. OptimalTransportationNetworks. ModelsandTheory.Berlín:Springer-Verlag,2009.(LectureNotesinMathematics;1955)

[34] Bertalmío,M.;Caselles,V.;Provenzi,E. «IssuesaboutRetinextheory andcontrastenhancement». Int.J.Comput.Vis.,83(1)(2009),101–119.

[35] Bertalmío,M.;Caselles,V.;Provenzi,E.;Rizzi,A. «Perceptualcolor correctionthroughvariationaltechniques». IEEETrans.ImageProcess., 16(4)(2007),1058–1072.

[36] Bertalmío,M.;Sapiro,G.;Caselles,V.;Ballester,C. «Imageinpainting».A: SIGGRAPH’00.Proceedingsofthe27thAnnualConference onComputerGraphicsandInteractiveTechniques.NovaYork:ACM Press/Addison-WesleyPublishingCo,2000,417–424.

[37] Bertsch,M.;DalPasso,R. «Hyperbolicphenomenainastronglydegenerateparabolicequation». Arch.RationalMech.Anal.,117(4)(1992), 349–387.

[38] Blake,A.;Zisserman,A. VisualReconstruction.Cambridge,MA:MIT Press,1987.(MITPressSeriesinArtiﬁcialIntelligence)

[39] Blanc,Ph. «Ontheregularityofthesolutionsofsomedegenerateparabolicequations». Comm.PartialDiﬀerentialEquations,18(5–6)(1993), 821–846.

[40] Brenier,Y. «ExtendedMonge-Kantorovichtheory».A: OptimalTransportationandApplications.Berlín:Springer,2003,91–121.(LectureNotesin Math.;1813)

[41] Buades,A.;Coll,B.;Morel,J.-M. «Anon-localalgorithmforimagedenoising».A: 2005IEEEComputerSocietyConferenceonComputerVision andPatternRecognition.Vol.2.Piscataway,NJ:IEEESignalProcessing Society,2005,60–65.

[42] Calderero,F.;Caselles,V. «MultiscaleanalysisforimagesonRiemannianmanifolds». SIAMJ.ImagingSci.,7(2)(2014),1108–1170.

[43] Calvo,J.;Campos,J.;Caselles,V.;Sánchez,O.;Soler,J. «Flux-saturated porousmediaequationsandapplications». EMSSurv.Math.Sci.,2(1) (2015),131–218.

[44] Calvo,J.;Campos,J.;Caselles,V.;Sánchez,O.;Soler,J. «Pattern formationinaﬂuxlimitedreaction-diﬀusionequationofporousmedia type». Invent.Math.,206(1)(2016),57–108.

[45] Calvo,J.;Campos,J.;Caselles,V.;Sánchez,Ó.;Soler,J. «Qualitative behaviourforﬂux-saturatedmechanisms:travellingwaves,waitingtime andsmoothingeﬀects». J.Eur.Math.Soc.(JEMS),19(2)(2017),441–472.

[46] Calvo,J.;Caselles,V. «Local-in-timeregularityresultsforsomeﬂuxlimiteddiﬀusionequationsofporousmediatype». NonlinearAnal.,93 (2013),236–272.

[47] Campos,J.;Guerrero,P.;Sánchez,Ó.;Soler,J. «Ontheanalysisof travelingwavestoanonlinearﬂuxlimitedreaction-diﬀusionequation». Ann.Inst.H.PoincaréAnal.NonLinéaire,30(1)(2013),141–155.

[48] Carrillo,J.A.;Caselles,V.;Moll,S. «Ontherelativisticheatequationinonespacedimension». Proc.Lond.Math.Soc.(3),107(6)(2013), 1395–1423.

[49] Caselles,V. «AcharacterizationofweaklysequentiallycompleteBanach lattices». Math.Z.,190(3)(1985),379–385.

[50] Caselles,V. «OnirreducibleoperatorsonBanachlattices». Nederl.Akad. Wetensch.Indag.Math.,48(1)(1986),11–16.

[51] Caselles,V. «Ontheperipheralspectrumofpositiveoperators». Israel J.Math.,58(2)(1987),144–160.

[52] Caselles,V. «Dunford-PettisoperatorsandtheRadon-Nikodýmproperty». Arch.Math.(Basel),50(2)(1988),183–188.

[53] Caselles,V. «AshortproofoftheequivalenceofKMPandRNPinBanach latticesandpredualsofvonNeumannalgebras». Proc.Amer.Math.Soc., 102(4)(1988),973–974.

[54] Caselles,V. «AnextensionofAndo-Krieger’stheoremtoorderedBanach spaces». Proc.Amer.Math.Soc.,103(4)(1988),1070–1072.

[55] Caselles,V. «AcharacterizationofdualBanachlattices». Nederl.Akad. Wetensch.Indag.Math.,51(1)(1989),35–47.

[56] Caselles,V. «ScalarconservationlawsandHamilton-Jacobiequationsin one-spacevariable». NonlinearAnal.,18(5)(1992),461–469.

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

[57] Caselles,V. «Convergenceofthe‘relativistic’heatequationtotheheat equationas c →∞». Publ.Mat.,51(1)(2007),121–142.

[58] Caselles,V. «Ontheentropyconditionsforsomefluxlimiteddiffusion equations». J.DifferentialEquations,250(8)(2011),3311–3348.

[59] Caselles,V. «Fluxlimitedgeneralizedporousmediadiﬀusionequations». Publ.Mat.,57(1)(2013),155–217.

[60] Caselles,V. «Convergenceofﬂux-limitedporousmediadiﬀusionequationstotheirclassicalcounterpart». Ann.Sc.Norm.Super.PisaCl.Sci.(5), 14(2)(2015),481–505.

[61] Caselles,V.;Catté,F.;Coll,T.;Dibos,F. «Ageometricmodelforactive contoursinimageprocessing». Numer.Math.,66(1)(1993),1–31.

[62] Caselles,V.;Chambolle,A.;Novaga,M. «UniquenessoftheCheeger setofaconvexbody». PaciﬁcJ.Math.,232(1)(2007),77–90.

[63] Caselles,V.;Coll,B.;Morel,J.-M. «AKanizsaprogramme».A: VariationalMethodsforDiscontinuousStructures.Basilea:Birkhäuser,1996, 35–55.(Progr.NonlinearDiﬀerentialEquationsAppl.;25)

[64] Caselles,V.;Haro,G.;Sapiro,G.;Verdera,J. «Ongeometricvariational modelsforinpaintingsurfaceholes». Comput.Vis.ImageUnd.,111(3) (2008),351–373.

[65] Caselles,V.;Igual,L.;Sander,O. «Anaxiomaticapproachtoscalar datainterpolationonsurfaces». Numer.Math.,102(3)(2006),383–411.

[66] Caselles,V.;Kimmel,R.;Sapiro,G. «Geodesicactivecontours». Int. J.Comput.Vis.,22(1)(1997),61–79.

[67] Caselles,V.;Kimmel,R.;Sapiro,G.;Sbert,C. «Minimalsurfaces:a geometricthree-dimensionalsegmentationapproach». Numer.Math., 77(4)(1997),423–451.

[68] Caselles,V.;Kimmel,R.;Sapiro,G.;Sbert,C. «Minimalsurfacesbased objectsegmentation». IEEETrans.PatternAnal.Mach.Intell.,19(4)(1997), 394–398.

[69] Caselles,V.;Klaiany,C. «Existence,uniquenessandregularityfor Kruzkov’ssolutionsoftheBurger-Carleman’ssystem». Ann.Fac.Sci. ToulouseMath.(5),10(1)(1989),93–104.

[70] Caselles,V.;Miranda,M.,Jr.;Novaga,M. «TotalvariationandCheeger setsinGaussspace». J.Funct.Anal.,259(6)(2010),1491–1516.

[71] Caselles,V.;Monasse,P. GeometricDescriptionofImagesasTopographicMaps.Berlín:Springer-Verlag,2010.(LectureNotesinMathematics;1984)

[72] Caselles,V.;Morel,J.-M.;Sbert,C. «Anaxiomaticapproachtoimage interpolation». IEEETrans.ImageProcess.,7(3)(1998),376–386.

[73] Crandall,M.G.;Ishii,H.;Lions,P.-L. «User’sguidetoviscositysolutionsofsecondorderpartialdiﬀerentialequations». Bull.Amer.Math. Soc.(N.S.),27(1)(1992),1–67.

[74] DalPasso,R. «Uniquenessoftheentropysolutionofastronglydegenerateparabolicequation». Comm.PartialDiﬀerentialEquations,18(1–2) (1993),265–279.

[75] Demanet,L.;Song,B.;Chan,T. «Imageinpaintingbycorrespondence maps:adeterministicapproach». UCLACAMReport,03-40(2003),1–17.

[76] Dubrovin,B.A.;Fomenko,A.T.;Novikov,S.P. ModernGeometryMethodsandApplications.PartI.TheGeometryofSurfaces,TransformationGroups,andFields.NovaYork:Springer-Verlag,1984.(Graduate TextsinMathematics;93).[TraduïtdelrusperRobertG.Burns]

[77] Efros,A.A.;Leung,T.K. «Texturesynthesisbynon-parametricsampling».A: ProceedingsoftheSeventhIEEEInternationalConferenceon ComputerVision.Vol.2.Piscataway,NJ:IEEESignalProcessingSociety, 1999,1033–1038.

[78] Facciolo,G.;Arias,P.;Caselles,P.;Sapiro,G. «Exemplar-basedinterpolationofsparselysampledimages».A: EMMCVPR’09.Proceedingsof the7thInternationalConferenceonEnergyMinimizationMethodsinComputerVisionandPatternRecognition.Berlín;Heidelberg:Springer-Verlag, 2009,331–344.(LectureNotesinComputerScience;5681)

[79] Fedorov,V.;Arias,P.;Facciolo,G.;Ballester,C. «Aﬃneinvariant self-similarityforexemplar-basedinpainting».A: Proceedingsofthe11th JointConferenceonComputerVision,ImagingandComputerGraphics TheoryandApplications.Vol.3.Setúbal,Portugal:ScienceandTechnology Publications,Lda,2016,48–58.

[80] Fedorov,V.;Arias,P.;Sadek,R.;Facciolo,G.;Ballester,C. «Linear multiscaleanalysisofsimilaritiesbetweenimagesonRiemannianmanifolds:practicalformulaandaﬃnecovariantmetrics». SIAMJ.Imaging Sci.,8(3)(2015),2021–2069.

[81] Ferradans,S.;Palma-Amestoy,R.;Provenzi,E. «Analgorithmicanalysisofvariationalmodelsforperceptuallocalcontrastenhancement». IPOLJ.ImageProcess.Online,5(2015),219–233.

[82] Gilboa,G.;Osher,S. «Nonlocallinearimageregularizationandsupervisedsegmentation». MultiscaleModel.Simul.,6(2)(2007),595–630.

[83] Gonzalez,R.C.;Woods,R.E. DigitalImageProcessing.2aed.Upper SaddleRiver:PrenticeHall,2002.

[84] Gronchi,G.;Provenzi,E. «Avariationalmodelforcontext-driveneﬀects inperceptionandcognition». J.Math.Psych.,77(2017),124–141.

[85] Kass,M.;Witkin,A.;Terzopoulos,D. «Snakes:Activecontourmodels». Int.J.Comput.Vis.,1(4)(1988),321–331.

[86] Kawai,N.;Sato,T.;Yokoya,N. «Imageinpaintingconsideringbrightness changeandspatiallocalityoftexturesanditsevaluation».A: Proceedings PSIVT2009:AdvancesinImageandVideoTechnology.Berlín;Heidelberg: Springer,2009,271–282.(LectureNotesinComputerScience;5414)

P.Arias,C.Ballester,B.Coll,J.M.MazóniE.Provenzi

[87] Land,E.H.;McCann,J.J. «LightnessandRetinextheory». J.Opt.Soc. Amer.,61(1)(1971),1–11.

[88] Malladi,R.;Sethian,J.A.;Vemuri,B.C. «Evolutionaryfrontsfor topology-independentshapemodelingandrecovery».A: ComputerVision-ECCV’94.Berlín;Heidelberg:Springer,1994,1–13.(LectureNotes inComputerScience;800)

[89] Malladi,R.;Sethian,J.A.;Vemuri,B.C. «Shapemodelingwithfront propagation:alevelsetapproach». IIEEETrans.PatternAnal.Mach.Intell., 17(2)(1995),158–175.

[90] Masnou,S.;Morel,J.-M. «Levellinesbaseddisocclusion».A: Proceedings1998InternationalConferenceonImageProcessing.ICIP98 Vol.3.Piscataway,NJ:IEEESignalProcessingSociety,1998,259–263.

[91] Mihalas,D.;Mihalas,B.W. FoundationsofRadiationHydrodynamics NovaYork:OxfordUniversityPress,1984.

[92] Osher,S.J.;Sethian,J.A. «Frontspropagationwithcurvaturedependent speed:AlgorithmsbasedonHamilton-Jacobiformulations». J.Comput. Phys.,79(1988),12–49.

[93] Palma-Amestoy,R.;Provenzi,E.;Bertalmío,M.;Caselles,V. «Aperceptuallyinspiredvariationalframeworkforcolorenhancement». IEEE Trans.PatternAnal.Mach.Intell.,31(3)(2009),458–474.

[94] Provenzi,E.;Caselles,V. «Awaveletperspectiveonvariational perceptually-inspiredcolorenhancement». Int.J.Comput.Vis.,106(2) (2014),153–171.

[95] Provenzi,E.;DeCarli,L.;Rizzi,A.;Marini,D. «Mathematicaldeﬁnition andanalysisoftheRetinexalgorithm». J.Opt.Soc.Amer.A,22(12) (2005),2613–2621.

[96] Rizzi,A.;Gatta,C.;Marini,D. «Anewalgorithmforunsupervised globalandlocalcolorcorrection». PatternRecognitionLett.,24(11)(2003), 1663–1677.

[97] Rosenau,P. «Tempereddiﬀusion:Atransportprocesswithpropagating frontandinertialdelay». Phys.Rev.A,46(1992),7371–7374.

[98] Rudin,L.I.;Osher,S.;Fatemi,E. «Nonlineartotalvariationbasednoise removalalgorithms». Phys.D,60(1–4)(1992),259–268.

[99] Sander,O.;Caselles,V.;Bertalmio,M. «Axiomaticscalardatainterpolationonmanifolds».A: Proceedings2003InternationalConferenceon ImageProcessing.Vol.2.Piscataway,NJ:IEEESignalProcessingSociety, 2003,III–681–4.

[100] Sapiro,G.;Caselles,V. «Histogrammodificationviadifferentialequations». J.DifferentialEquations,135(2)(1997),238–268.

[101] Sethian,J.A. «Numericalalgorithmsforpropagatinginterfaces: Hamilton-Jacobiequationsandconservationlaws». J.DiﬀerentialGeom.,31(1)(1990),131–161.

[102] Terzopoulos,D.;Witkin,A.;Kass,M. «Constraintsondeformablemodels:Recovering3dshapeandnonrigidmotion». ArtiﬁcialIntelligence, 36(1)(1988),91–123.

[103] Verdera,J.;Caselles,V.;Bertalmio,M.;Sapiro,G. «Inpaintingsurface holes».A: Proceedings2003InternationalConferenceonImageProcessing Vol.3.Piscataway,NJ:IEEESignalProcessingSociety,2003,II–903–6.

[104] Wexler,Y.;Shechtman,E.;Irani,M. «Space-timecompletionofvideo». IEEETrans.PatternAnal.Mach.Intell.,29(3)(2007),463–476.

P.Arias

CMLA

UniversitéParisSaclay France pablo.arias@cmla.ens-cachan.fr

C.Ballester

Dept.deTecnologiesdelaInformacióilesComunicacions UniversitatPompeuFabra Barcelona,Spain coloma.ballester@upf.edu

B.Coll

Dept.deMatemàtiquesiInformàtica UniversitatdelesIllesBalears EscolaPolitècnicaSuperior 07122 Palma,Spain tomeu.coll@uib.cat

J.M.Mazón

Dept.d’AnàlisiMatemàtica UniversitatdeValència 46100 Burjassot,Spain Jose.M.Mazon@uv.es

E.Provenzi

IMBInstitutdeMathématiquesdeBordeaux UniversitéBordeaux,UMR 5251 France

edoardo.provenzi@u-bordeaux.fr

ButlletídelaSocietatCatalanadeMatemàtiques Vol.33,núm.1,2018.Pàg.43–55. DOI:10.2436/20.2002.01.79

PonceletalapresódeSaratov

JoanCarlesNaranjo

...j’auraispuintitulercetouvrage,purementmathématique, Mémoiresd’outre-tombe;c’est,eneﬀet,lefruitdesméditations d’unjeunelieutenantdugénie,laissépour mortsurlefunestechampdebataillede Krasnoï,nonloindeSmolensk,... (delprefaci d’Applicationsd’analyseetdegéométrie J.-V.Poncelet)

Resum: PonceletvaserunmilitarfrancèsquevaformarpartdelestropesnapoleòniquesquevanperdrelabatalladeKrasnialacampanyadeRússia.Durantel seucaptiverialapresódeSaratov,basant-seenelrecorddeleslliçonsinspiradores deGaspardMongeal’ÉcolePolytechnique,vareﬂexionarsobreelsfonamentsdela geometriaprojectivaienvadonarunpuntdevistaoriginalqueacabaràtenintunagran inﬂuènciaeneldesenvolupamentdelageometriaalllargdelsegle xix.Entreelsseus resultats,elmésconegutésl’anomenat porismadePoncelet,queestudial’existència depolígonsambvèrtexsenunacònica C icostatstangentsaunaaltracònica D en funciódelaposiciórelativade C i D.Enaquestarticlerepassemalgunsfetsdelavida dePonceletidonemlaidead’unademostraciódelporisma.

Paraulesclau: geometriaprojectiva,còniques,porismadePoncelet.

ClassiﬁcacióMSC2010: 01A55,14N05,14N15.

1Ponceletilageometriaprojectiva

Tothomcreaapartirdelqueconeix.Permoltoriginalquesiguilapropostai nouelllenguatgeresultaimpossibledesfer-sedelesparaulesidelsconceptes

Aquestarticleesbasaenlalliçóinauguraldelcursacadèmic2017–2018delaFacultatde MatemàtiquesiInformàticadelaUniversitatdeBarcelona,impartidaperl’autor.

JoanCarlesNaranjo

apresosiquesónpartdelmotlledel’obranova.Encaraméssiparlemde matemàtiques.ComjaensfeianotarNewton:ésdifícilmirarllunysenseposar elspeussobrelesespatllesdelsqueensprecedeixen.QuanJean-VictorPoncelet, unjovetinentdel’exèrcitnapoleònicformatal’ÉcolePolytechnique,ésfet presonerdesprésdelabatalladeKrasnidedicaelseutempsalapresóde Saratovaestudiarlespropietatsdelesﬁguresgeomètriques.Recordemles sevesparaules:

...privéqu’ilétaitdetoutlivre,detoutinstrumentdeprécision,difficilesàse procurerdanscettevilledeSaratoff,d’ailleursdépourvuealorsdebibliothèques scientifiques.Onnedoitdoncpass’attendreàrencontrericicommelerefletou l’écholointaindesprofondstravauxanalytiquesdesEuler,desBernouilli,des Huygens,desNewton,desd’Alembert,etc.,nimêmedestravauxplusrécentset nonmoinsadmirablesdesLagrange,desLegendre,desLaplace,desMongeet deleursdisciples,travauxquin’avaientlaisséaucunetracedanssamémoireau milieudespérilsetdesangoissesd’unaussimalheureuxdébutdanslacarrière desarmes.

Ésadir,quetotiserunhomebeninformatdelsavençosanticsirecents elseuaïllamenteldesproveeixdelesfontsbibliogràﬁquessobrelesquals puguibasarelsseusestudis.Enelsseustreballsnoméstrobarem,diuell, ecos llunyans d’aquestesobresfonamentals.Lesmatemàtiquesquerecordatenen lesarrelsenleslliçonsinspiradoresdeMonge.Aquestseràelseupuntde partidaaSaratov.Elseumotllementalseràlageometria.

PercomprendrequèfaPonceletalapresódeSaratovicomhiarribaﬁns allàcalentendreelmomenthistòricenquèvaviureiquinavaserl’evolucióde lageometriaenelsseglesprecedents.

Jean-VictorPoncelet(1788–1867).

Ponceletneixunanyabansdel’esclatdelaRevolucióFrancesa,esdevenimentquemarcaràlavidadetotselsmatemàticsdelasevageneracióidela

precedent.Unabonapartdelsmillorsmatemàticsdel’èpocaestrobenaFrança el1789imoltsesposicionenpolíticament,algunsmoltactivament.EspecialmentsigniﬁcantéselcasdeGaspardMonge,ques’integradinsdelmoviment jacobíiocupacàrrecsdediversaimportànciadurantladècadadelsnoranta,i arribaaserministredeNapoleóiundelshomescapdavantersenlasevaexpedicióafricana(vaserelprimerpresidentdel’Institutd’Egipte).Mongeparticipa activamentenlacreaciódel’ÉcolePolytecniquein’esdevéeldirector.Està consideratl’inventordelageometriadescriptivaifaaportacionsimportants aldesenvolupamentdelageometriadiferencialidelateoriad’equacionsen derivadesparcials.

D’altrabanda,l’estatdelageometriaalfinaldelsegle xviii éshereudels desenvolupantsfonamentalsdel’inicidelsegle xvii.Aladècadadel1630, desprésdelarecuperaciódelamatemàticagregadurantelRenaixement, hihadosfets,gairebéparal.lels,quehandetenirunagraninfluènciaenel devenirdelageometriaienlasevaexplosiócomaciènciaconnectadaamb l’àlgebra,l’aritmètica,l’anàlisiilafísicadurantelssegles xix i xx.Elprimer éslapublicacióde LaGéometrie deDescartes,enquès’introdueixelconcepte moderndecoordenadescartesianes.L’èxitd’aquestatecnologianovíssimava serimmediatcombésabem.Ambpocadiferènciadetemps,Desarguespublica diversostreballssobrelespropietatsprojectivesdelesfiguresforçaignorats enelseumoment.TansolsPascalsegueixlarutadeDesarguesisemblaque durantunsegleimiglaconsideraciódelageometriaprojectivacomuna branca«especialitzada»enproblemesconcrets(propietatsqueesmantenen perprojecció)esmantindrà.FinsaPoncelet.

Jean-VictorPonceletnovaserunmatemàticprofessionalsinóunmilitar.Es vaformaral’ÉcolePolytechnique,onvarebreleslliçonsdegeometriadeMonge quetantl’influiran.EnacabarelsestudisvatornaraMetz,lasevaciutatnatal, pertreballareneldissenydelesfortificacionsdelaciutat.Cridatafiles,va formarpartdelestropesnapoleòniquesqueanavenalaconquestadeRússia. Tenia24anysquanvacaureferitalabatalladeKrasnilatardordel1812, unadelesmésgransdesfetesdel’Exèrcitfrancèsenaquellacampanya.Vaser empresonataSaratovielseucaptiverivadurarunanyimig;vanecessitar gairebésismesosperrefer-sedelesferides.Desprésdelacapitulacióde Napoleó,laprimaveradel1814,totselspresonersdeguerravanseralliberatsi PonceletvatornaraFrançapelseupropipeu.

Durantl’estadaaSaratovvadedicarelseutempsaensenyarmatemàtiques aaltrespresonersiaferrecercaengeometria.Comenaltrescasosalllargdela història(J.LerayoW.Rudin,perexemple),semblaquel’ocupacióintel.lectual, docentoderecerca,permetevadir-sedel’empresonamentfísic.Enelcasde Poncelet,l’aïllamentelvaportara«repensar»iaredescobrirelsfonamentsdela geometriaqueconeixiairecordava.Lasevainventivaioriginalitatconverteixen unexercicid’evasiómentalenungircopernicàenlaconcepciódelageometria projectiva.

JoanCarlesNaranjo

Lessevesinvestigacions,plasmadesanysméstard,el1882,enel Traité despropriétésprojectivesdesﬁgures (vegeu[9]),suposenlafonamentacióde lageometriaprojectivamoderna.Elprincipidedualitat,perexemple,apareix perprimeravegadaenaquesttractat.LesaportacionsposteriorsdeMöbius, VonStaudtiPlückerconnectaranlageometriaprojectivaamblestècniques analítiquesmitjançantlaintroducciódelescoordenadeshomogènies,itot plegatconstitueix(amblesaportacionsdelateoriadefuncionsalgebraiques d’AbelideRiemann)elfonamentsobreelqualesdesenvolupaicreixelque avuiconeixemcoma geometriaalgebraica.

2ElporismadePoncelet

EntreelsresultatsquePonceletdemostraenelseutractat,elmésrecordatés aquestapetitajoia:

PorismadePoncelet. Siguin C i D duescòniquesnodegeneradesdelpla projectiu(complex)sensecappuntdetangènciaentreelles.Suposemqueexisteix unpolígonde n costatsambvèrtexsa C icostatstangentsa D.Aleshorespera totpunt P de C existeixuntalpolígonqueté P entreelsseusvèrtexs.

Diremqueunpolígoncomeldel’enunciatésun n-polígondePonceletper a (C,D).Així,siunpentàgoncomeldeldibuixexisteix,aleshorestindrem inﬁnitspentàgons(5-polígonsdePoncelet).Ésmés,podremposarunvèrtexen laposicióqueensvinguimésdegust.

Unamaneradereformularl’enunciatéslasegüent:consideremunpunt p1 delacònica C itracemdesd’aquestpuntunarecta t1 tangenta D.Diem p2 l’altrepuntdetalldelarecta t1 amb C.Aradibuixeml’altratangenta D que passaper p2 ianomenem p3 elnoupuntdetallamb C,etc.

Elporismaensdiuquesialcapde n passostornemalpuntinicial,aleshores elmateixpassaràsicomencemlaiteracióenqualsevolaltrepunt.Pertant, l’existènciade n-polígonsdePonceletnomésdepèndelaposiciórelativadeles duescòniquesinopasdelpuntinicial.Observemquel’aﬁrmacióesfapera un n concret;potpassar(ipassa,comesdeduiràdelademostracióquefarem mésendavant)queexisteixin n-polígonsdePonceletiencanvinon’hihagi peraunaltrevalor m.Tambéésplausiblequenon’hihagiperacapvalor de n.Calfernotarqueelsdibuixosqueapareixenmésamuntsónunamica enganyosos:comqueestemtreballantsobreelscomplexosisuposemqueles còniquesnotenenpuntscomunsamblamateixatangent,aleshoresenrealitat lescòniques C i D estallentransversalmenten4puntsdiferents.

Elsignificatdelaparaula porisma mereixunamicad’atenció.Enlamatemàticamoderna,almenysdesdeSteiner,s’enténqueésunarelacióquesesatisfà peraunranginfinitdevalorsperònomésenpresènciad’unacertacondició. Ésadir,unporismaésunproblemaperalqualobéhihainfinitessolucionso bénon’hihacap,depenentdesisesatisfàunadeterminadacondició.Noés ladefinicióqueapareixalsdiccionaris(quanhiapareix),enquècuriosament podemllegiraccepcionsdeltipus«conjuntdecorol.larisqueesdedueixendela demostraciód’unteorema»quesemblenallunyadesdel’úsrealquetrobema labibliografiamatemàtica.Laparaulajaestrobaenlesobresdelsmatemàtics grecsfinsalpuntqueEuclidesvaescriuretresllibressobreporismesquehan desaparegut.Pappus(sis-centsanysposterioraEuclides)diuessencialmentel següent:

Elsporismesnosónformalmentniteoremesniproblemes,sinóqueocupen unaposicióintermèdiaentretotsdos,demaneraqueelsseusenunciatspoden serenformadeteoremesodeproblemes.[...]Peròésclarapartirdeles deﬁnicionsqueelsanticsgeòmetres[sic]entenienmoltmillorladiferència entrelestresclasses:enunteoremacalia provar elqueesproposava,enun problemas’haviade construir elqueesproposavai,ﬁnalment,enunporisma s’haviade trobar elqueesproposava.

JoanCarlesNaranjo

UnprecedentdelresultatdePonceletésla fórmuladeChapple,erròniamentatribuïdaaEulerdurantmoltdetemps.Responaunapreguntamolt natural:donatsdoscercles,uncontingutdinsl’altre(vegeueldibuix),enquines condicionsexisteixuntriangleinscritenuncercleicircumscrital’altre?La respostaéslafórmulaesmentada,queinvolucraladistància a entreelsdos centres,elradi r delcercleinteriorielradi R delcercleexterior: a2 = R2 2rR Observemqueenlarelaciónohiintervécapdadasobreeltriangle,comper exemplelaposiciód’undelsvèrtexs.Aixòésaixíperquèuncopsatisfeta larelacióexisteixeninﬁnitstrianglesinscritsicircumscritsalhora.Enunciat d’aquestamaneraésclaramentunporismaieldePonceletn’ésunaamplíssima generalització.

3Lacarta

Abansdedonarunademostraciódelporismafemunadarreraal lusióhistòrica apartird’unarticlemoltrecent.Alaintroduccióde[10]esdiu:

DuringhislasttriptoMoscow,thesecondauthorofthisarticlecameinto possessionofaremarkablemathematicalletter.Thecustodianoftheletter,a Russianbusinessmanwhowishedtoremainanonymous,presentedtheletter toTabachnikovattheendofhislecture[...]andexplainedthattheletterhad beenwrittenbyhisgreat-great-greatgrandfather,KonstantinShestakov,shortly afterhehadbeendischargedfromtheRussianArmyduringtheNapoleonic War.

Laprimerapartdel’articleéselcontingutd’aquestacartaquevaarribara lesmansdeTabachnikovd’unamanerataninusual.ElquehiexplicaKostantin Shestakovéspartdelessevesexperiènciescomamilitard’altagraduació destinataSaratovdurantelperíodeenquèPoncelets’hitrobapresoner.Ens diuqueallàlavidaeraduraperatothomdegutalfredintens,iqueamésa mésnohihaviacapaltreentretenimentquebeureenlestrescantinesquehi haviaalpoble.Reconeixques’halliuratdecaureenaquestarutinaalcohòlica perquèhatingutlasortquelihanassignatcomaassistentpersonalunjove

tinentfrancès,Poncelet,enamoratdelesmatemàtiques,queelfapartícipdeles sevesrecerques.Enparticular,liexplicaelseuporisma,queeldeixafascinat. Finsalpuntqueellmateix,tambéaﬁcionatalageometria,inicialesseves pròpiesinvestigacions.

Lacartaestàadreçadaalseugermàisuposadamentnoesvaarribaraenviar mai.Enrealitat,ésunapeticiód’ajuda.Ellhaviacomençataestudiar,fent càlculsenexemplesconcrets,comesmovienelsbaricentres(ialtrescentres demasses)dels n-polígonsdePonceletenmoureelsvèrtexs.Conjecturava queesmouensobreunacònicaperònovasaberdonar-neunademostraciói... quanescriulacartaPonceletjanohiés.Laraóperlaqualvapensarenelseu germàeraquesabiaquehaviaanatal’institutambunestudiantbrillantque esdevinguéprofessoruniversitariaKazan;estractavanimésnimenysquede Lobatxevski!Elseuprecésqueutilitziaquestcontacteperdemanarajudaper trobarunademostració.

SchwartziTabachnikovresolenlespreguntesqueproposaelmilitarrusi hopubliquenjuntamblahistòriadelacarta.

4Idead’unademostraciódelporisma

Elquepresentemacontinuacióésunadelesmoltesdemostracionsdelporisma, probablementunadelesmésdirectes,queinvolucratansolsalgunsfetsbàsics devariablecomplexaidelateoriadesuperfíciesdeRiemann.

Recordemquetotacònicanodegeneradatéassociadaunaaltracònica, anomenada cònicadual,queparametritzal’envolventdelacònica,osiguiel conjuntdetoteslesrectestangentsalacònica.Ditd’unaaltramanera,ﬁxada lacònica(vistacomunaequaciódesegongrauhomogèniaentresvariables), elscoeﬁcients (A,B,C) delesrectes Ax + By + Cz = 0tangentsalacònica tambésatisfanunaequaciódesegongrauhomogènia.

Considerem C i D duescòniquesnodegeneradesisigui D∗ lacònicadual de D.Deﬁnimelconjuntsegüent: S ={(p,l) ∈ C × D∗ | p

JoanCarlesNaranjo

Notemquelesprojeccionsencadafactorproporcionensenglesaplicacions deﬁnidesen S iambimatge C i D∗,respectivament.Lesdenotemper

π1 : S → C,π2 : S → D∗ .

Ésbenconegutquelescòniquescomplexesprojectivesnodegeneradessón superfíciesdeRiemanndegènerezero,ésadir,esferes.Lesfibresdeles aplicacions πi sónfàcilsd’entendre:fixatunpunt p ∈ C hihaexactament doselementsen S, (p,l), (p,l ) talsque π1(p,l) = π1(p,l ) = p,on l, l són lesduesrectesper p quesóntangentsa D.Diemque π1 ésunaaplicacióde grau2.Observemquehihaexactament4puntsde C,quetambésóna D, peralsquals l = l .Diemquesónpuntsderamificacióde π1.Unaanàlisi semblantpodemfer-ladel’aplicació π2,tambédegrau2iamb4puntsderamificació.Usantlesduesaplicacionsésfàcildeduirque S ésunasuperfíciede Riemanncompactaiconnexai,enparticular,unasuperfícietopològicaconnexa, compactaiorientable.Percalcular-neelgènereusemelresultatsegüent:

FórmuladeRiemann-Hurwitz(engrau 2). Sigui f : S1 → S2 unaaplicaciódegrau2entresuperfíciesdeRiemanndegèneres g(S1) i g(S2) amb r puntsderamiﬁcació.Aleshores2g(S1) 2 = 2(2g(S2) 2) + r .

Enelnostrecas(f = π1, S1 = S i S2 = C)tenimque r és4i,comhem dit,elgènerede C és0.Pertant, g(S) = 1,ésadir, S ésuntor,oditd’una altramanera,elproductededuescircumferències.L’estructuradegrupde lacircumferència S 1 ⊂ C induïdapelproductedenombrescomplexesdota també S d’estructuradegrup.

Unfetfonamentalperalademostracióésque S estàdotadadedues involucions σ i τ,ésadir,duesaplicacionsholomorfes σ,τ : S → S queno sónlaidentitatperòsatisfanque σ 2 = τ 2 = IdS .Lesdeﬁnicionssónmolt simples: σ aplicaunelement (p,l) ∈ S al’element (p ,l),on p ésl’altretall de l i C; τ aplica (p,l) ∈ S al’element (p,l ) on l ésl’altratangenta D que passaper p.

(p,l) ∈ S σ(p,l) = (p ,l) τσ(p,l) = (p ,l )

Lacomposiciódelesduesinvolucionsrealitzal’accióquehemexplicatquan hemditqueelporismaespotentendrecomunprocésiteratiu.Enparticular,la iteraciócomençadaenelpunt p ∈ C tornaalmateixpuntdesprésde n passos (osigui,existeixun n-polígondePonceletpera (C,D) demaneraque p sigui undelsseusvèrtexs)siinoméssi

(τ ◦ σ)n(p) = p.

Necessitemaraellemasegüentqueésforçaconegutiqueadmetremsense demostració.

Lema 4.1. UnainvolucióenunasuperfíciedeRiemanndegènere 1 ésuna translacióobéunatranslaciómultiplicadaper 1

Notemquelestranslacionsnotenenpuntsfixos,mentrequelesnostres involucionsentenen.Perexemple,si p ∈ C ∩ D iprenemcoma l latangent a D en p,elpunt (p,l) de S ésfixper σ .Ésadir,queelspuntsderamificació de π1 sónpuntsfixosdelainvolució σ .Deixemallectorelpetitexercicide trobarpuntsfixosper τ.Endefinitiva, σ i τ sóndelaforma IdS seguides d’unatranslaciói,pertant, τ ◦ σ ésunatranslacióen S,osigui τ ◦ σ = tα,on: tα : S → S,p tα(p) = p + α.

Aixílacondició (τ ◦ σ)n(p) = p esreescriucom nα = 0,queésindependent delpunt p.Aixòacabalademostraciódelporisma.

Aquestademostracióestàdesenvolupadaambtotdetall,incloseslesbases delateoriadesuperfíciesdeRiemann,enelllibre[5].Laideadelademostració ésdegudaaP.GriﬃthsiJ.Harris(vegeu[7]i[8]).

Observacions

a) El1913Gerbaldi(vegeu[3])vacalcularelnombredecòniques C delfeix generatper C i D peralesqualshiha n-polígonsdePonceletpera (C ,D) Aquestnombreéslameitatdelnombredepuntsde n-torsióprimitius d’unacorbael.líptica.Aixòesdedueixfàcilmentdelademostracióque hemdonat.

b) Delademostraciótambéesdesprènquenoéscompatiblel’existència de n ide m-polígonsdePonceletpera C, D si n i m sónprimersentre si.Tambés’obtéquesilatranslació τ ◦ σ noésdetorsió,nohihaurà n-polígonsdePonceletperacap n.

c) CayleyvarespondreunstrentaanysdesprésdeltractatdePonceletauna preguntanaturalqueesderivadelporisma:espotdonarunacondició explícitaperal’existènciad’un n-polígon?Lasevarespostaéslasegüent: anomenem MC i MD lesmatriussimètriquesassociadesalescòniquesi consideremelpolinomidetercergrau:

p(x) := det(xMC + MD).

JoanCarlesNaranjo

ConsideremeldesenvolupamentdeTaylordelafunció p(x) en x = 0:

0 + A1x + A2x2 + A3x3 +···

Cayleydemostraqueexisteixun n-polígondePonceletpera (C,D) si inoméssi:

Alacúbicaplana y 2 = p(x) sel’anomena cúbicadeCayley.Ambunamica defeinaespotprovarquelasuperfíciedeRiemann S delademostració ésisomorfaalacompletacióprojectivadelacúbicadeCayley.

5Altresdemostracionsialtresporismes

LademostracióoriginaldePoncelettéduesparts:laprimeraéslacomprovació ambcoordenadesenelcasdecerclesilasegonaéslageneralitzacióacòniques qualssevolmitjançantdeterminadestransformacionsprojectives(projeccions centrals).Pelcamíutilitzaelcontrovertit«principidecontinuïtat»queté moltprotagonismeenelseutractat.Probablementperquèaquestprincipi novaseradmèspermoltsmatemàticsdel’èpocahivahaverintentsde demostracióalternatiusdemoltstipus.UndelsmésconegutséseldeJacobi: construeixunafuncióel.lípticaassociadaalproblemaperalcasdedoscercles. Lademostraciódelporismautilitzapropietatsformalsd’aquestesfuncions. Nombrosostreballsdel’èpocaintentenestendrelesideesdeJacobialcas general.AltresdemostracionsigeneralitzacionsvanserdonadesperLebesgue, Halphen,Hurwitz...(vegeu[3]).

Durantelsegle xx l’interèspelporismanodecau,comdemostren,per exemple,lesfórmulesdeGerbaldi.Alsanyssetanta,dostreballsdeGriﬃthsi Harrisatreuendenoul’atenciósobreeltema.Nonomésdonenduesdemostracionspuramentalgebraiques(unadelesqualshempresentataquí),sinóque generalitzenelporismaalcasdeplanstangentsaquàdriquesdel’espai.Enels anysnoranta,BarthiMichel(vegeu[2])relacionenl’existènciadepolígonsde Ponceletambpropietatsdemodelsplansdecertescorbesmodulars.

AbandadelporismadeGriﬃthsiHarrisentrobemmoltsd’altresalaliteratura,algunsdemoltclàssics.UndelsmésinteressantséseldeWeyrreferenta sistemesdegeneratriusdeduesquàdriques.Enl’article[1]esdemostraaquest porismais’obtéeldePonceletcomacorol lari.Moltsporismesclàssicstenen aveureamblesanomenades sèriescirculars (teoremadelzig-zag,porisma d’Emch...);undelsmésestèticséseldeSteiner,quepassemaenunciaramb detall.

Anomenem cercle qualsevolequaciódelaforma

a(x2 + y 2) + bx + cy + d = 0,a,b,c,d ∈ C

Lescoordenadeshomogènies (a : b : c : d) deﬁneixenl’espaiqueparametritza aquestscercles,queésunespaiprojectiu P3.Fixatuncercle C,elconjunt delscerclestangentsa C ésuncon QC ⊂ P3.Donatunaltrecercle D,els cons QC , QD estallenenduescòniques C1, C2.Enpoquesparaules,elconjunt delscerclestangentsadoscerclesdonatss’agrupenenduesfamílies,cadascuna parametritzadaperunacònica.Perexemple,eneldibuixsegüentprenemun cercled’unadelesfamílies(diguem-ne

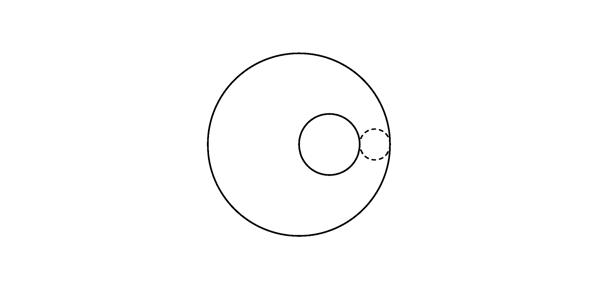
CDS1

Ésfàcilvisualitzarcomsónelscerclesdel’altrafamília,laparametritzada per C2:sóncerclestangentsa enelseuinterior.

Perseguirendavantsuposemﬁxadalafamília C1 entotalaconstrucció.A continuació,triemunaltrecercle S2 en C1 (automàticamenttangenta C ia D) quetambésiguitangenta ;n’hihadosdepossibles,delsqualsentriemun:

CDS1

JoanCarlesNaranjo

Considerem S3 ∈ C1 tangenta S2.Aral’eleccióésúnicasidemanemno tornarenrere,ésadir,que S3 ≠ S1.Seguintaquestmètodeconstruïmuna successiódecercles S ,S ,S ,S ∈ C :

S’obtéelresultatsegüent:

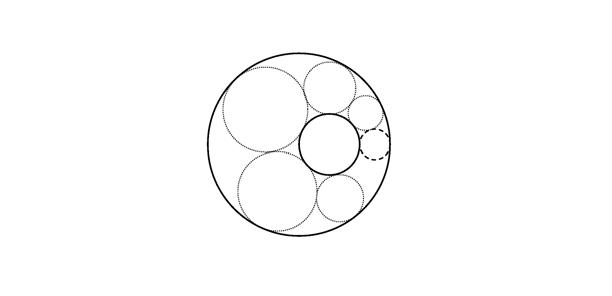
PorismadeSteiner. Silasuccessiódecerclesdescritaanteriormenttanca desprésde n passos,osigui S1 = Sn,aleshoreshofasempre,independentment delcercle S1 inicialmentescollit.

Espotdonarunademostraciód’aquestporismamoltsemblantalaquehem donatdeldePoncelet(vegeu[1]).

6Comentarisbibliogràﬁcs

PeraprofundirenelcontexthistòricimatemàticdelavidadePonceletprobablementlareferènciaméscompletasigui[6];l’abastdelllibreésmoltmés ampliqueaquestperíodejaquedescriul’evoluciódelageometriaalllargde totelsegle xix.L’article[3],publicatenduesparts,contéunaaproximació matemàticamoltexhaustivaalporismairecullprecedents,provesdediversostipus,generalitzacionsiinfluènciesenresultatsrecents;labibliografia éscompletíssima.Enelsarticles[7]i[8]hihaunademostraciópurament algebraicogeomètricasenseutilitzarmètodestranscendents.Tambéhiapareix unageneralitzaciódelporismaal’espaidedimensió3.Recollintelmateix puntdevista,quasivintanysdespréstrobem[1],enquèesrecullendiverses generalitzacionshistòriquesiresultatsrelacionats.Espresentenidemostren sotaunmarcunificat.

LaiteracióqueapareixenelporismadePonceletestàemparentadaamb algunsproblemesclàssicsdesistemesdinàmics,especialmentl’anomenat «problemadelsbillarsel líptics».Untractamentintroductoriaaquestproblema espottrobaralﬁnaldelllibre[5].Peraunestudimésprofundellectorespot adreçara[4].

Referències

[1] Barth,W.;Bauer,Th. «Poncelettheorems». Exposition.Math.,14(2) (1996),125–144.

[2] Barth,W.;Michel,J. «ModularcurvesandPonceletpolygons». Math. Ann.,295(1)(1993),25–49.

[3] DelCentina,A. «Poncelet’sporism:alongstoryofreneweddiscoveries,II». Arch.Hist.ExactSci.,70(2)(2016),123–173.

[4] Dragovi´c,V.;Radnovi´c,M. PonceletPorismsandBeyond.Integrable Billiards,HyperellipticJacobiansandPencilsofQuadrics.Basilea:Birkhäuser/SpringerBaselAG,2011.(FrontiersinMathematics)

[5] Flatto,L. Poncelet’sTheorem.Providence,RI:AmericanMathematical Society,2009.

[6] Gray,J. WorldsoutofNothing.ACourseintheHistoryofGeometryinthe 19thCentury.2aed.Londres:Springer-VerlagLondon,Ltd.,2011.(Springer UndergraduateMathematicsSeries)

[7] Griffiths,P.;Harris,J. «APoncelettheoreminspace». Comment.Math. Helv.,52(2)(1977),145–160.

[8] Griffiths,P.;Harris,J. «OnCayley’sexplicitsolutiontoPoncelet’sporism». Enseign.Math.(2),24(1–2)(1978),31–40.

[9] Poncelet,J.V. Traitédespropriétésprojectivesdesﬁgures.París:Gauthier-Villars,1822.[Reeditatenlacol.lecció«LesGrandsClassiques Gauthier-Villars»]

[10] Schwartz,R.;Tabachnikov,S. «CentersofmassofPonceletpolygons, 200yearsafter». Math.Intelligencer,38(2)(2016),29–34.

DepartamentdeMatemàtiquesiInformàtica UniversitatdeBarcelona

Spain

jcnaranjo@ub.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.33,núm.1,2018.Pàg.57–80. DOI:10.2436/20.2002.01.80

Elsprimers,desvelats

XavierXarles

Resum: L’objectiuprincipaldel’articleésintroduirdemanerainformalunpunt devistaprobabilísticenladistribuciódelsnúmerosprimers,quepodriaexplicarper quèalgunesdelesconjecturesmésconegudessobreelsprimerssóncertes.També presentemalgunesideesqueexpliquenperquèaquestaaproximacióreﬂecteixencerta maneral’autènticadistribuciódelsprimers.Pelcamíintroduïmalgunsdelsresultats mésrecentssobreelsprimersdegutsaGreen,Tao,ZhangiPolymath.

Paraulesclau: primers,funciózeta,ènuplesprimeres,pseudoaleatori,conjecturade Goldbach,conjecturadeDePolignac,teoremadeZhang.

ClassiﬁcacióMSC2010: 11-02,11A41,11P32.

1Introducció

Elsnúmerosprimersestrobenentreelsobjectesmatemàticsméssimples imésestudiats.Però,alhora,encararomanencobertsperunveldemisteri. Sembladifícilconciliarelfetquesiguinunobjectetanelementalialhoratan esmunyedíscomperestarpoblatdemultituddeconjectures.

Enaquestbreuarticlevoldriaexplicarque,defet,coneixemmoltbéels númerosprimers,quepodemdonarmoltsdetallssobrelasevadistribució idecidirambmoltaaproximacióquantsnúmerosprimershihacomplintuna propietatdeterminada,encaraquesovintnosabemcomdemostrarlesnostres aﬁrmacions(que,d’altrabanda,podemveriﬁcarnumèricament).Ditd’unaaltra manera,coneixemmoltbél’estructurasubjacentdelconjuntdelsnúmeros primers,totiquedevegadesnoentenimdemostracionsformalmentcorrectes.

Aquestarticleesbasaenlalliçóinauguraldelcursacadèmic2017–2018delsgrausdematemàtiques,físicaimatemàtiques,estadísticaaplicadaiestadísticaaplicadaisociologiadela UniversitatAutònomadeBarcelona,impartidaperl’autor.

Elpuntclau,ialhorasorprenent,éslanaturalesaaparentmentaleatòriadels númerosprimers,totiestarperfectamentdeterminats.Diemqueelsnúmeros primerstenenunadistribuciópseudoaleatòria:esdistribueixendelamateixa maneraquehofariennúmerosescollitsal’atzarseguintunesrestriccions bàsiqueselementals.

Exposarembreumentunmodelaleatori(essencialmentdegutaHaraldCramer),explicantl’heurísticaqueeljustiﬁca,iendeduiremconjecturesdegudes aHardyiaLittlewood.Alﬁnalparlaremdelsavençosrecentsenlademostració d’algunsd’aquestsresultats.

Potserpotsorprendreallectorquediguiquehihamatemàticsqueconeixen moltbéalgunfenomendelqualnotenenunademostració;semblaqueaixò xoquiamblaideamoltestesaqueelsmatemàticsnoenscreiemresqueno estiguirigorosamentdemostrat.Peròlamajoriadematemàticsprofessionals queconec(notots!)creuenlaveracitatdelesconjecturesméspopularsimés profundes,inoperquèalguness’hagincomprovatnumèricament(totique aixòtambéhiajuda),sinóperquèsónconseqüènciadecerteshipòtesismolt profundesquehomveucomanaturals,seguramentboniquesenuncertsentit delaparaula,difícild’explicarperòmoltvívid,iquealhoraexpliquenresultats conegutsielsdonenunsentit.

Exordi

Totidedicar-meal’aritmèticadesquevaigcomençarlatesi(opotserunparell d’anysabans),elsnúmerosprimersnohanestatmaiunsobjectesenelsquals pensésgaire.Defet,durantmoltsanysdelamevarecerca,elsnúmerosprimers erentansolsunalletra,habitualment p,avegades q,sovint ,quesortiaarreu enelsarticlesillibresquellegia,ienelsproblemesenquètreballava.Una anècdotafamosad’AlexanderGrothendieckil lustraforçabélamevarelació d’aleshoresambelsnúmerosprimers.Lallegendaexplicaqueenunaconversa ambunaltrematemàtic,durantlaqualGrothendieckutilitzavatotal’estonaun númeroprimer p indeterminat,l’interlocutorlivademanarsipodiaagafar unnúmeroprimerparticular.Grothendiecklivapreguntarsiesreferiaaun númeroprimerconcret,idesprésvadir:«D’acord,agafael57».1

Lamevarelacióambelsprimers,però,vaanarcanviantperdiversosmotius. Primer,gràciesalSeminarideTeoriadeNombresdeBarcelona(UB-UAB-UPC), enelquall’any2005vàremestudiarelsmètodesdegarbell,ienconcretla demostraciódelteoremadeChen.Ambl’ajudadeJorgeJiméneziFernando Chamizovaigpoderentendreforçamillord’onsortialaconjecturaexplícita delsnúmerosprimersbessons.TambéhedemencionarAndrewGranville,tant pelsseusarticlesdedivulgaciócompelsdiversosmissatgesintercanviatsal llargdelsanys.

Ensegonlloc,iseguramentdegutalapublicaciódelamevalliçóinaugural sobrelaconjecturaABC,vaigcomençararebremissatgesoﬁnsitotvisites

1Aquestl’anomenenel primerdeGrothendieck

aldespatxdepersones(desd’aﬁcionatsﬁnsamatemàticsmésprofessionals) queemfeienpreguntessobrenúmerosprimers,m’explicavenresultatsque havienobtingutom’enviavenescritsambmètodesodemostracions.Apartir deferconsultes,dellegirarticlesidepensar-hisovintemvaigferunaidea forçabonadequèsesabiaferalapràcticaambelsnúmerosprimers,ialhora dequèsabiarealmentlagentdelmeuvoltant.

2Quantsprimershiha?

Undelsresultatsclàssicsdelesmatemàtiquesambunademostraciómés conegudaipopularésprobablement2 degutaEuclides[6].És,sensecapdubte, unadelesprimeresdemostracionsrealmentinteressantsquehomveuquan començaaestudiarmatemàtiques.

Teorema 2.1. Hihainﬁnitsnúmerosprimers.

Percert,sovints’explicalaideaequivocadaqueEuclidesvademostrarel seuteoremaperreduccióal’absurd.Però,defet,elquevademostrarésque, donatqualsevolconjuntfinitfixatdenúmerosprimers,hihaunnúmeroprimer (calculable!)nocontingutenelconjuntfixat.

Totiquehompodriapensarqueelresultatd’Euclidesrespondeltotala preguntadequantsnúmerosprimershiha,defetnoensdonacapindicació sobrecomesdistribueixenelsprimers.Perexemple,noresponalapreguntade quantsnúmerosprimersrealmenthihaamb,posem,1000xifresdecimals.Si bééscertqueespotextreuredelademostracióunafitainferiorperalnombre deprimersinferiorsaunnúmerodonat x,laques’obtéd’aquestamanera estàmoltllunydelarealitat.Esvahaverd’esperaraLegendre,queel1797va conjecturarquehihaviaaproximadament n/(log(n) + A) númerosprimersinferiorsa n,peracertaconstant A (queellvaestimaren A =−1.08366d’acord ambunestaulesdeprimersquetenia).3 Defet,Gaussjahaviaconjecturatuns anysabans,el1792,quanteniasetzeanys,4 unresultatanàlegperòamb A = 0. SemblaqueGaussvadeduirlasevaconjecturaestudianttaulesdeprimers de1000en1000(pertaldesuavitzarels«errorsexperimentals»)finsadeduir quelaprobabilitatqueunnúmeromenorque n siguiprimerésasimptòticament1/ log(n).AixíhodescriualacartaescritaalseualumneJ.F.Enckelanit deNadaldel1849,enquèexplicacomvaferaquestaextrapolació(vegeula figura1).

2 Elprimertestimoniescritdelteoremaquetenimésseu,peròelselementsd’Euclidesrecollien moltsdelsresultatsdematemàtiquesconegutsﬁnsaquellmomentinopodemdescartarque l’autororiginalsiguiunaltre.

3Usarélogperadenotarellogaritmeneperià.

4AgraeixoaJ.Girbauquem’ajudésaconﬁrmaraquestfet.

Figura 1: ExtractedelacartadeGaussaEncke.

AquestaconjecturavaserdemostradasimultàniamentidemaneraindependentperJacquesHadamard[11]iCharles-JeandelaValléePoussin[4] l’any1896,basant-seenlesideesintroduïdesperP.L.Txebixev5 isobretoten lesdeG.F.B.Riemann.

Teoremadelsnúmerosprimers. Sidenotemper π(x) laquantitatdenúmerosprimersmenorsoigualsque x,amb x ≥ 2,aleshores

π(x) ∼ x log(x)

Lanotació f(x) ∼ g(x) perafuncionsdevariablerealvoldràdirque lim x→∞ f(x) g(x) = 1,

totiquelainterpretaremdientque f(x) i g(x) són,pera x grans,aproximadamentiguals.

Podeminterpretaraquestresultatcomunaestimacióaproximadadela probabilitatqueunnúmeroentersiguiprimer.Aquestaestimacióésmés exactaamesuraqueelnúmero n esfamésgran.Hoposaréenformade principi.

Principi 2.2. Laprobabilitatqueunenterentre 1 i n siguiprimerésaproximadament 1 log(n)

3Elsnúmerosprimersilafunciózeta

Lademostracióméshabitualdelteoremadelsnúmerosprimerspassaper veureprimerquelafunciózetadeRiemann,deﬁnidaperunasumainﬁnita,

ζ(s) := ∞ n=1 1 ns ,

5Sí,éselmateixquevademostrarladesigualtatdeTxebixevenprobabilitat.

on s ∈ C ésunnúmerocomplexambpartreal > 1(pertalquelasumasigui convergent),espotestendreaunafuncióatotselscomplexosaexcepcióde l’1,inotécapzeroambpartrealiguala1.Quelafuncióespotestendreatots elscomplexoshovademostrarelmateixRiemann,quealhoravaferlahipòtesi (oconjectura)quetotselszerosambpartrealpositivatenenlapartrealigual a1/2(lafamosíssimahipòtesideRiemann).

Pertaldecomprendre,niquesiguidemaneraintuïtiva,compotserque laquantitatdenúmerosprimerstinguialgunarelacióamblalocalitzaciódels zerosd’aquestafunciócomplexa,elquefaremprimeréssimplificarl’afirmació delteoremadelsnúmerosprimers.Sienllocdecomptarelsnúmerosprimers finsa x,elscomptemperòaraacadaprimer p liassignemelpes log(p), aleshoresobtenimlafunció

Θ(x) := p≤x log(p),

ques’anomenalafunció Θ deTxebixev.Elqueensdiuelteoremaaleshoresés quelagràﬁcadelafunció Θ(x) éscomlarecta y = x,osigui Θ(x) ∼ x.

Ara,quinarelacióhihaentreque Θ(x) ∼ x ilaposiciódelszerosdela funciózeta?DoncsjustamentaixòéselquevadescobrirRiemannamblaseva famosafórmulaexplícita(quenovaserdemostradarigorosamentfinsmés endavant,el1895,pervonMangoldt).Perapoderescriure-lacorrectament necessitemmodificarlleugeramentlafunció Θ(x),demaneraquenocanviarà elseucomportamental’infinit,peròestornaràunamicamésllisa.

Modiﬁcaremlafunció Θ deTxebixevendospassos:primerposantel pes log(p) nonomésalsnúmerosprimers p,sinótambéalessevespotències pn;obtenimlafunció

Ψ (x) := pn≤x log(p) (onelsumatoriesmouentreelsprimers p ielsenters n ≥ 1),anomenadala Ψ deTxebixev.Seguidament,encanviaremelvalorenelspuntsonhihaunsalt (lespotènciesdelsprimers pn),posantcomavalorelvalormitjàdelsalt:per tant,deﬁnim Ψ0(x) := Ψ (x) si x noésiguala pn,on p ésprimeri n ≥ 1enter, i Ψ0(pn) := Ψ (pn) 1/2log(p).Ésfàcilveure(deveritat!)que Θ(x) ∼ Ψ0(x).

Figura 2: La Ψ deTxebixev.

Ara,lafórmulaexplícitadeRiemannensdiuque

Ψ0(x) = x ρ xρ ρ log(2π) 1 2 log(1 x 2),

onelsumatoriéssobreelszeros ρ delafunciózetadeRiemannambpartreal positiva(tambédits zerosnotrivials).Observeuque log(2π) = ζ (0) ζ(0) ,cosaque d’algunamanerajustiﬁcal’apariciód’aquestnúmeroalafórmula.

Elpuntclaudelademostraciódelteoremadelsnúmerosprimersésveure quetotselszerosambpartrealpositivadelafunciózetadeRiemanntenen lapartrealmenorque1.Defet,sisabéssimquetotselszerosnotrivials tenenpartrealiguala1/2,aleshoresdeduiríemque

i,pertant,que

|Ψ0(x) x|= O(√x log(x)), cosaqueensdiuquinésl’errorquefemquanaproximemlafunció Ψ0(x) per x Delamateixamanera,lacertesadelahipòtesideRiemannensdonariaunaﬁta moltbonadel’errorfetenaproximar π(x) per x/ log(x)

Arabé,d’onsurtlafórmulaexplícita?Doncssurtessencialmentd’expressar lafunciózetadeRiemanncomaproductededuesmaneresdiferents:com aproductesobreelsprimers,perunabanda(elproducted’Euler),icoma productesobreelsseuszeros,perl’altra(elproductedeWeierstrass).En aplicarladerivadalogarítmicaalsdoscostatsdelaigualtat,obtenimdues fórmulespera ζ(s)/ζ (s),ilaidentitatqueresultajacontélainformació buscada,peròenscalextreure-la.Perfer-hointegremcontralafunció xs /s ihi apliquemelteoremadelsresidusdeCauchy.

Perexemple,lafunció 1 2 log(1 x 2) surtdelsaltreszerosdelafunciózeta (elszerostrivials),quesónelsentersparellsnegatius,jaque

1 2 log(1 x 2) = ∞ n=1 x 2n 2n , aixíquelafórmulaexplícitadefetespotescriurecom Ψ0(x) = x

ζ (0) ζ(0) , onara ρ esmoudinsde tots elszerosdelafunció ζ,ila x corresponaconsiderar xξ /ξ,on ξ esmoudinsdetotselspolsde ζ (quenomésn’hihaun, iés ξ = 1).

Enpodeutrobarmoltsmésdetallsiunainformaciómoltexhaustivaen l’articledeJ.Querdel2007publicatal ButlletídelaSocietatCatalanade Matemàtiques [17].

4Conjecturesambnúmerosprimers

Totssabemquehihamultituddeconjecturessobrenúmerosprimers,ialgunessón,defet,delesmésfamosesdelesmatemàtiques.N’explicaremalgunes, toticórrerelriscd’avorrirellector.

Nohesabuttrobarelnomdelapersonaquevaformularlaprimeraconjectura.6 Enl’argotdel’oﬁcidiemqueés«folklore»,enelmateixsentitque diemquecertconteocertacançóhosónquannosabemquienvaserl’autor original.

Conjecturadelsprimersbessons. Hihainﬁnitsprimers p talsque p + 2 és primer.

Elsparellsdenúmerosprimers p i q talque q = p + 2s’anomenen primers bessons.Perexemple,lesparellesdeprimersbessonsinferiorsa100són (3, 5),(5, 7),(11, 13),(17, 19),(29, 31),(41, 43),(59, 61),(71, 73).

ConjecturadeGoldbach. Totnúmeroenterparell ≥ 4 éssumadedosnúmerosprimers.

GoldbachvaconjecturarenunacartaaEulerel1742quetotnúmeroenter (positiu)erasumadecomamolttresnúmerosprimers(totiqueellconsiderava elnúmero1comanúmeroprimer).Eulermateixvadir«quetotnúmeroparell éssumadedosnúmerosprimershoconsiderounteorematotalmentcert,toti quenoelpucdemostrar».

Laconjecturasegüentésunageneralitzaciónaturaldelaconjecturadels primersbessonsfetaperDePolignacel1849.

ConjecturadeDePolignac. Donatunnúmeroparell n,hihainﬁnitsnúmerosprimers p talque p + n éstambéprimer.

Observeuquelacondicióque n siguiparellésnecessària,jaquesi n és senari p ésprimersenar,aleshores p + n ésparellinopotserprimer.

Perexemple,pera n = 4lesparellesobtingudesamb p ≤ 100són

(3, 7),(7, 11),(13, 17),(19, 23),(37, 41),(43, 47),(67, 71),(79, 83),(97, 101), ipera n = 6(elsanomenats primers«sexy»)n’hihaforçamés:

(5, 11),(7, 13),(11, 17),(13, 19),(17, 23),(23, 29),(31, 37),(37, 43), (41, 47),(47, 53),(53, 59),(61, 67),(67, 73),(73, 79),(83, 89),(97, 103).

Explicaremaquestfenomenaparentmentsorprenentmésendavant.

LaconjecturasegüentésatribuïdaaLegendre.

ConjecturadeLegendre. Peratotnúmeroenter n ≥ 2,hihaalgunnúmero primer p talque n2 <p<(n + 1)2

6 Totiquesemblaqueelprimerautilitzarelnomde primersbessons vaserP.Stäckelel1916, A.DePolignacjahaviaaﬁrmatlasevaconjecturamésgeneralel1849[5].

Hompotveureque,defet,nonoméséscertaperaalgunprimer,sinó quehoésperamolts.Perexemple,si n = 100,hiha1228númerosprimers entre1002 i1012.Semblacuriósque,totiquealapràcticaesperemunnombre creixentdeprimersentre n2 i (n + 1)2,siguemincapaçosdedemostrarque n’hihaalmenysun!

Finalment,enunallistaquevaferLandauel1912delsproblemesinatacables hiapareixlaconjecturasegüent:

Conjecturadelsprimersvoraquadrats. Hihainﬁnitsnúmerosprimers delaforma n2 + 1,pera n unenter(parell).

Perexemple,ﬁnsa10000hihaelsprimersvoraquadratssegüents:5,17, 37,101,197,257,401,577,677,1297,1601,2917,3137,4357,5477,7057, 8101i8837.

Veuremcommoltesd’aquestesconjecturesestaníntimamentrelacionades, ique,defet,sónconseqüèncianaturaldelahipòtesiquediuqueelsnúmeros primersestandistribuïtscomsifossinnúmerosaleatorissotaunescertes restriccions.

5Tenirconjecturesnovoldirnosaberres: elscasosconeguts

Apartdemoltsresultatsnumèricsqueencertamanerapodrienreaﬁrmarles conjecturesanteriors,tenimtambéresultatsteòricsobtingutsenselsdarrers anysques’hiaproximenforça.

Perexemple,sabemquelaconjecturadelsprimersbessons(iladeDePolignac)éscertasipermetemnonomésnúmerosprimers,sinónúmerosquesón productedecomamoltdosprimers(anomenatsavegades quasiprimers).

Teorema 5 1 (Chen). Peratotnúmeroparell n,hihainﬁnitsnúmerosprimers p talque p + n ésprimeroproductededosprimers.

Enelmateixarticle[2]esprovaquelaconjecturadeGoldbachéscertapera númerosprougrans(moltgrans!)siamésespermetqueundelsdosnúmeros siguiquasiprimer.Podeuveuretambéelvolumcorresponentdel19èSeminari deTeoriadeNombresdeBarcelona[10].

Teorema 5.2 (Chen). Totnúmeroparellprougranéssumad’unnúmeroprimeriunnúmeroqueésprimeroproductededosprimers.

ElmateixChenvademostrarl’any1975a[3]laconjecturadeLegendreper aquasiprimersenllocdeprimers.Utilitzantunargumentsimilar,H.Iwaniec vademostrarquehihainﬁnitsquasiprimersvoraquadrats[13].

TambésabemquelaconseqüènciasegüentdelaconjecturadeGoldbach (que,defet,s’anomenavala conjecturadèbildeGoldbach)éscerta.

Teorema 5 3 (Vinogradov,Helfgott). Totnúmerosenar(> 5)éssumade tresnúmerosprimers.

ElteoremavaserdemostratperI.M.Vinogradov[19]el1937peraun númerosenarmésgranqueunnúmeroexplícitenorme(massagranpera permetrelacomprovaciónumèricadelteoremaperalsnúmerosméspetits),7 i,desprésdemilloressubstancialsenelsmètodes,H.Helfgott,unmatemàtic peruà,elvapoderprovarperatotselsnúmerosl’any2013.

FinalmentdestacoelteoremarecentdeY.Zhang,quevaanunciarel2013,i vasermilloratsubstancialmentperMaynardiPolymath.Alesúltimesseccions discutiréaquestúltimresultat,iexplicaréalgunesanècdotesalseuvoltant.

Teorema 5.4 (Zhang,Maynard,Polymath). LaconjecturadeDePolignacés certaperaalgun 2 ≤ n ≤ 246.

6Tenirconjecturesnovoldirnosaberres: lesconjecturesquantitatives

Totiqueespodriapensarquenopodemdemostrarquehihainﬁnitsprimers bessonsperquèsónforçaescassos,oquenosabemlaconjecturadeGoldbach perquèelsnúmerosparellssónsumadedosprimersdepoquesmaneres,de fet(semblaque)totelcontrariéscert:hihamoltessolucionsenambdóscasos.

L’any1923,G.H.HardyiJ.E.Littlewoodvanconjecturar,basant-seenuna anàlisiheurísticadeladistribuciódeprimers,fórmulesaproximadesperal nombredeprimersbessonsinferiorsoigualsa x [12].

G.H.HardyiJ.E.Littlewood.

Conjectura 6.1. Sidenotemper π2(x) laquantitatdenúmerosprimersbessonsméspetitsque x,aleshores

Laconstant Π2 s’anomenala constantdelsprimersbessonsdeHardyLittlewood. Delamateixamanera,vanconjecturardequantesformesespotescriure unnúmeroparellcomasumadedosnúmerosprimers.

Conjectura 6.2. Sidenotemper G2(n) laquantitatdeparellesdenúmeros primers (p,q) talsque n = p + q,on n ésunnúmeroparell,aleshores

Observeuquealaconjecturahiapareixaltravegadalaconstant Π2

Defet,hihaversionsquantitativesdelaconjecturadeDePolignac,que comentaremmésavall,aixícomdelesaltresconjectures,enlesqualsnohi entrarem.

Lapreguntaclaués:podemdonarunaexplicacióuniﬁcadadetotesaquestes conjectures,ialhoraexplicarperquèsónplausibles?

Veuremqueésperfectamentpossiblefer-hopartintd’unasuposiciómolt natural:elsnúmerosprimersescomportencomanúmerosaleatorisseguint unmodeldeterminat.

7L’heurísticadelsprimers

AnalitzaremlafórmulaconjecturadaperHardyiLittlewoodperalnombrede primersbessons.

Partimdelteoremadelsnúmerosprimers,quejustiﬁcaquelaprobabilitat queunnúmeroentre1i n siguiprimerés«aproximadament»iguala1/ log(n).

Laideaésquesielfetque p siguiprimerésindependentdelfetque p + 2 siguiprimer,laprobabilitatque p i p + 2siguinprimersalhorahadeserel productedelesprobabilitatsrespectives,i,pertant,1/(ln(n))2 peralsnúmeros entersal’interval [1,n].

Perònosónindependents,jaquesi p ésprimer, p + 2éssenar,i,pertant, ésmésprobablequesiguiprimer.Delamateixamanera,si p = 3m + 1és primer,aleshores p + 2noésprimer,jaque3eldivideix.

Perpodertreure’nunafórmula,elquefaremésunmodel«aleatori»més aproximat,quedependràd’unenter w «petit»,iuncopentinguemconseqüènciesfaremellímitquan w creix.

Perexemple,elmodelamb w = 2consisteixadirquelaprobabilitatqueun número n siguiprimerés0si n ésparell,i2/ log(n) si n éssenar(donatque unnúmeroprimermésgranque2maiésparell).

Elmodelperaun w generaléselsegüent:diremquelaprobabilitatqueun número n siguiprimerés0siésdivisibleperunprimer p ≤ w,iés

enaltrecas.

Aracalcularemelnombredeprimersbessonsenaquestmodeldepenent de w,sotalahipòtesid’independènciamencionadaabans.Obtenim

onelfactor2ésdegutalfetquesi p ésprimer,aleshores p + 2éssenar,iel factor p 2 p ésdegutalfetquesitenim p númerosconsecutius,només p 2 podenserelprimermésgrand’unaparelladeprimersbessons(jaqueelsque sóncongruentsamb0oamb2mòdul p nohopodenser).Fixeu-vosaraqueen ferellímitquan w vaainﬁnitobtenim

i,pertant,lafórmuladelaconjectura.

Unaaltrainterpretació,potserméssenzilla,éslasegüent:donatqueels esdevenimentsque p siguiprimerique p + 2siguiprimernosónindependents, hemd’afegir-hiunfactordecorrecció,tenintencompteladivisibilitatmòdul primers q «petits».Laprobabilitatque q divideixiunenter n és1/q;per tant,laprobabilitatquenohofaciés1 1/q.Pertant,laprobabilitatque dosentersescollitsal’atzarnosiguindivisiblespera q és (1 1/q)2.Ara, laprobabilitatque q nodivideixini p ni p + 2éslaprobabilitatque p ≡ 0, 2 (mod q),queés,peraunnúmeroal’atzar,iguala1 2/q si q> 2,i1/2 si q = 2.Pertant,elfactordecorreccióquecalposarpera q = 2és

ipera q> 2de

Ladivisibilitatperprimersdiferentssónclaramentcondicionsindependents (pelteoremaxinèsdelesrestes),aixíquecalprendreelproductedelsfactors decorrecció.Finalment,hihaelproblemadeﬁnsaquinsprimerspetitscal considerar,però noimporta,jaqueelproductedelsfactorsdecorrecciópera totselsprimers«grans»ésmoltpropera1inoalteraelresultat.

8Unexemple:laconjecturadeDePolignacquantitativa

Comqueseguramentl’argumentheurísticanteriornoushadeixatdeltot convençuts(hefetelquehepogutperatransmetrelaideaenpoquesparaules), intentaréexplicar-vosunargumentsimilarperòméssenzillquerelaciona laconjecturadelsprimersbessonsambladeDePolignacperaunnúmero parell n qualsevol.Primerdescriuremunaconseqüènciadecertesconjectures deHardyiLittlewoodmésgeneralsquelesconjectures6.1i6.2.

Conjectura 8.1. Donatunnúmeroparellqualsevol n,denotemper πn(x) el nombredeprimers p ≤ x talque p + n ésprimer.Aleshores

(x), on q esmoudinsdelsprimerssenarsquedivideixen n Perexemple,laconjecturaensdiriaque π2(x) i π4(x) són(aproximadament)iguals,iencanvi π6(x) éseldoblede π2(x),i,pertant,hihaeldoble deprimerstalsque p + 6ésprimerquedeprimerstalsque p + 2ésprimer.

Laconjecturalapodemcomprovarperaalgunsvalorsde n.Perexemple, π2(100) = 8, π4(100) = 9i π6(100) = 17.I π2(1000) = 35, π4(1000) = 42i π6(1000) = 74.D’altrabanda,aixònoensexplicaperquè π2(x) i π4(x) són aproximadamentiguals,però π6(x) ésaproximadamenteldoble.

Unargumentheurísticquehojustiﬁcaéselsegüent:si a ésunnúmeroa l’atzar,aleshores3téprobabilitat2/3dedividir a o a + 2,perònomés1/3de dividir a o a + 6,pertant,elsegonparelltéeldobledeprobabilitatd’estar formatperdosprimers.

Elmateixtipusd’argumentjustiﬁcalaconjecturaengeneral.

9Elsprimerssónpseudoaleatoris

Ésclarqueelsnúmerosprimersnosónaleatorisencapsentitdelaparaula: estanperfectamentdeterminats!Quèvolemdir,pertant,quandiemquesón pseudoaleatoris?Volemdir,perexemple,queelspodemdescriureutilitzant modelsaleatoris,iobtenirrespostesques’ajustenproubéalarealitata preguntesqueenspodemformular.

Perexemple,sisabéssimqueelsprimersesdistribueixenaleatòriament ambdensitatalvoltantde x igual1/ log(x) (queésunaaltramaneradeparlar delaprobabilitatdeserprimer),aleshoresuncàlculelemental(quenofarem) ensdonariaquelafórmuladelsnúmerosprimersméspetitsoigualsa x esdevé

π(x) = x 1 dt log(t) + O(√x log(x)), onelsegonterme«d’error»ensdiuquel’errorquefemenaproximaruna funcióperl’altreésméspetitqueunaconstantpera √x log(x)

Doncsresultaqueaquestafórmula,deduïdadelasuposicióqueelsprimers segueixenunadistribucióaleatòria,és,defet,comjahemcomentatabans, equivalentalahipòtesideRiemann.

Algúpodriapensarquesemblapocplausiblequesitriemnúmerosaleatòriamentacabaremtenintprounúmerosmoltapropentreells(queéselque ensdiulaconjecturadelsprimersbessons),peròtotprobabilistaexpertsap queaixòésunaintuïciófalsa!Sihomescullprounúmerosal’atzar,hihauna probabilitatforçaaltaquealgunsacabinsentpropersentresi.L’únicquecal tenirencompteésqueelsprimersnopodenestar«massaaprop»,jaqueno podenestaradistància1(osenar),permotiusaritmètics.

Unaaltramanerad’entendreperquèelsprimersescomportencoma númerosaleatorisambcertesrestriccionsésdirque,defet,coneixemtotesles restriccionsquehiha,iquenohihaconspiracionsocultesentreells.

Perexemple,imaginemquefoscertqueelsnúmerosprimersprougrans sempreacabessinen1enbase3(osigui,fossincongruentsamb1mòdul3). Aleshoreslaconjecturadelsprimersbessonsnopodriasercerta,jaqueencap parelladeprimersbessons p i p + 2podenserelsdosnúmeroscongruents amb1mòdul3.Peròresultaquesabemqueaquestahipòtesiésfalsa!De fet,sabemqueésfalsaentotabase:hihainﬁnitsprimersacabatsenla xifra b<a enbase a semprequenohihagicapnúmeroquedivideixi a i b alhora.AquestésunteoremadegutaDirichletquecomentaremmésendavant (vegeuelteorema12.2),iquedefetdiuqueaméselsprimersesdistribueixen demaneraequiprobableperacada a entoteslespossiblesterminacions b primeresamb a.Perexemple,tenimqueunaquartapart(aproximadament) delsprimersacabenen1,unaaltraen3,unaaltraen5iunaúltimaen7. Podeminterpretarque,defet,Vinogradov[19]vapoderdemostrarelseu teoremagràciesalfetquel’úsdel’anàlisideFourierielmètodedelcercle(degut aHardyiLittlewood,peròaparentmentbasatenunaideadeRamanujan)8 li permetéprovarquenohihaviaaltresconspiracionsquepoguessinferfalsa laconjecturadèbil(oternària)deGoldbach.Aixòéselquearaperarasom incapaçosdeferenelcasdelaconjectura(binària)deGoldbach.

10Defet,podemdemostrarqueelsprimersgairebéhosón, depseudoaleatoris

L’abrildel’any2004,BenGreeniTerenceTaovanenviaral’arxiudepreprints arxiv unarticleenquèesdemostravaunaconjecturaplantejadafeiamésde 230anyssobreelsnúmerosprimers[9].Elseuresultateraquehihasuccessions denúmerosprimersarbitràriamentllarguesenprogressióaritmètica.

Perexemple,quen’hihadellargada3ésfàcil:3,5i7(ambraó2).Ide llargada4també:5,11,17,23ambraó6,quedefetespotallargarunpasmés amb29.Dellargada10hiha199,409,619,829,1039,1249,1459,1669,1879, 2089ambraó210.Lasuccessióaritmèticadeprimersexplícitamésllargaque esconeixtélongitud26.

8 Podeuveurelapel lícula L’homequeconeixial’inﬁnit enquès’explicaambdetalllesrelacions entreells.

ElquevarendemostrarGreeniTaoésque,totiquenolessabemtrobar explícitament,n’hihadellargadatangrancomvulguem.Iperprovar-hovaren veurequeelsprimersespodenaproximarforçabéperconjuntspseudoaleatoris.

LademostraciódeGreeniTaocomençavaestenentelfamósresultatde Szemerédisobreprogressionsaritmètiques.Recordemqueladensitat(superior) d’unsubconjunt A delsnúmerosnaturals N estàdeﬁnidaper

δ(A) := limsup N→∞ |A ∩{1,...,N}| N .

Teorema 10.1 (Szemerédi). Siunsubconjunt A ⊂ N delsnúmerosnaturalsté densitatsuperior δ(A)> 0,aleshores A contésuccessionsaritmètiquesarbitràriamentllargues.

Ensagradariapoderaplicarelteoremaalconjuntdelsnúmerosprimers, peròresultaqueaquestconjunttédensitat0.

Laideaésveurearaqueelssubconjuntsdelsnaturalsque,totitenir densitat0,tenenuncomportament(pseudo)aleatori,tambécompleixenel teoremaanterior.

Engeneral,podemdeﬁnirladensitatrelativade A ⊂ S ⊂ N com

δS (A) := limsup N→∞ |A ∩{1,...,N}| |S ∩{1,...,N}| .

ElteoremarelatiudeSzemerédiquevarendemostrarGreeniTaodiuelmateix, peròaraperaconjuntspseudoaleatoris.

Teorema 10.2. Si S ⊂ N satisfàunacondiciódepseudoaleatorietatdeterminada, aleshorestotsubconjunt A ⊂ S amb δS (A)> 0 contésuccessionsaritmètiques arbitràriamentllargues.

Aquestresultat,compodeuveure,nofareferènciaalsnúmerosprimers. Defet,elqueestractadeveureésqueelconjunt A espotaproximarenun certsentitperunconjunt A de N ambdensitatpositiva,detalmaneraqueel nombredeprogressionsaritmètiquesen A ien A sónigualsexcepteperun factordenormalitzaciócontrolat.

Pertaldedemostrarelresultatquevolienrespectedelsnúmerosprimers, aGreeniaTaojasolselsquedavaconstruirunconjuntpseudoaleatori(en elsentitdelteoremaanterior)denúmeros«gairebéprimers»,demaneraque continguéselsnúmerosprimersambdensitatpositiva.9 Aquestconjuntes construeixcomençantperampliaradequadamentelsprimerspertalqueno hihagilesrestriccionsaritmètiquesquehemtrobatabans,comaraquetot primer = 2éssenar.Osigui,trobantunconjuntqueesdistribueixidemanera prouuniformemòdul n peratot n,peròquealhoracontinguielsnúmeros

9 Defet,elconjuntqueconsiderenestàdirectamentrelacionatambelsquasiprimers,osigui productesd’unodosprimers.

primersambdensitatpositiva.Idespréscalampliar-lounamicaméspertalde complirlacondiciónecessàriadelteorema.Persermésprecisos,elqueesfaés treballarnoambconjunts,sinóambconjuntsambpesos,cosaquesimpliﬁcala demostració.Noexplicaremaquíaquestaconstrucció,ques’haanatsimpliﬁcant enelsdarrersanys.

Defet,TaoiZiegler,l’any2008,varenmillorarnotablementelteorema10.2[18],demostrantqueperatot k ≥ 1itotacol.lecciódepolinomis P1(x),...,Pk(x) ∈ Z[x] ambcoeficientsentersisensetermeconstant(osigui que P1(0) =···= Pk(0) = 0),hihainfinitsenters m i n ≥ 1demaneraqueels números m + Pi(n) pera i = 1finsa k sóntotsprimers.Elcasdelteoremade Green-Taocorresponaprendreelspolinomis Pi(x) = (i 1)x.Noteuquela condiciósobreeltermeconstantnohauriadeseressencial,sinóunademenys restrictivaqueexploraremalasecciósegüent,iaquíjustamentésonrauel puntfeble(perdir-hod’algunamanera)delresultat.Perexemple,l’enunciat delteoremadeTaoiZiegleramb k = 2ielspolinomis P1(x) = 0i P2(x) = 2 (quenocompleixenlesseveshipòtesis)éslaconjecturadelsprimersbessons.

11Constel.lacionsdeprimers

Simireutaulesdeprimers,veureuquedetantentantapareixenprimers consecutiusambunitats1,3,7i9.Perexemple,11,13,17i19;101,103,107 i109,i191,193,197i199.Aquestssónexemplesdeconstel.lacionsdeprimers dediàmetre4.

Aixícomhemvistquepertalquehihagiinfinitsprimers p talque p+n sigui primerenscalque n siguiparell,tambéenspodempreguntarquintipusde condicionsnaturalshihasobreunallistad’enters0 ≤ n1 <n2 < ··· <nd per talquehipuguihaverinfinitsnúmerosenters x talsque x + ni siguinprimers peratot i ∈{1,...,d}.Aixòcorrespondriaaentendrequinescondicionss’han deverificarpertalqueunresultatequivalentaldeTaoiZieglerdelasecció anterior,peròaraperapolinomisconstants,puguisercert.

Elpuntclauquecalobservar,quegeneralitzaelfetquesi n éssenar, aleshoresdelparell p, p + n,n’hihaunqueésmultiplede2,éselsegüent:si hihaunnúmeroprimer q talque q divideix (m + n1) ··· (m + nd) peratot m ∈ Z,aleshoresnohipothaverinﬁnitsenters x amb x + ni primerperatot i, jaquealmenysunseràdivisibleper q.Untalnúmeroprimer q l’anomenarem una obstruccióalpatró

0 ≤ n1 <n2 < <nd.

Perexemple,nohipothaverinﬁnitsprimers p talque p + 2i p + 4siguin ambdósprimers.Defet,nomésn’hihaun: p = 3,amb p + 2 = 5i p + 4 = 7. Aixòésdegutalfetque3sempredivideix m(m + 2)(m + 4) peratot m ∈ Z; osiguique3ésunaobstruccióperalpatró0 < 2 < 4.Encanvi,nohihacap númeroprimer q quedivideixi f(n) := n(n + 2)(n + 6) peratot n,fetque podemcomprovarfàcilment,jaque f(1) = 21i f(2) = 26,quesónprimers entreells.

Unpatró

0 ≤ n1 <n2 < ··· <nd quenotinguicapobstrucció q ésuncandidatpossibleatrobarinﬁnitsenters x talsque x + ni ésprimerperatot i,o,ditd’unaaltramanera,quehihagi inﬁnitesdàtuplesdeprimersseguintelpatródonat.I,efectivament,aixòésel queprediul’heurísticaielmodelaleatori.Aquestaconjecturavaserformulada perDicksonel1904.

Conjecturadelesènuplesprimeres. Donatunpatró 0 ≤ n1 <n2 < ··· < nd senseobstruccions,hihainﬁnitsenters x ≥ 1 talsque x + ni ésprimerpera tot i = 1,...,d.

Ditd’unaaltramanera,elconjuntdevalorsentersquegenerenprimers seguintunpatródonatésinﬁnit.Sideﬁnim

Pn1<n2<···<nd := x ∈ Z≥1 : x + ni ésprimerperatot i ∈{1,...,d} , aleshoreslaconjecturaensdiuque Pn1<n2< <nd ésunconjuntinﬁnit.De fet,comabans,hihaunaconjecturaexplícitaqueensdeterminademanera asimptòticaquantselementstindria Pn1<n2< <nd ﬁnsaun y donat(aixòho veuremalaproperasecció).

Observeutambéqueenspodemreduiraconsiderarelspatronsamb n1 = 0, ialeshoreselquebusquemsónnúmerosprimerstalsque p + ni ésprimer peratot i = 2,...,d,osiguiqueelconjuntanteriorésunsubconjuntdels númerosprimers.

Donatunpatró0 = n1 < ··· <nd,enspodempreguntarperaun d ﬁxat quinésel nd méspetitdemaneraqueobtinguemunpatrósenseobstruccions. Perexemple,si d = 2elpatróméspetités0 < 2,isi d = 3,tenimdospatrons 0 < 2 < 6i0 < 4 < 6amb n3 = 6.Una constel.laciódeprimers dediàmetre d ésunpatrósenseobstruccionsdediàmetre d amb nd mínim.Perposar-neun exemplemés,unaconstel.lacióambdiàmetre4tépatró0 < 2 < 6 < 8(queens donarienelsexemplesanteriorsdeprimersconsecutiusacabatsen1,3,7i9),i unadediàmetre5és0 < 4 < 6 < 10 < 12.Espotveurequeperatot d ≥ 3hi hamésd’unaconstel.laciódediàmetre d

Laconjecturaanteriornoestàdemostradaperacappatrósenseobstruccions,peròelresultatdeZhang,queveuremmésendavant(teorema13.2),dona unaaproximacióaaquestaconjectura:apartird’uncertvalorde d explícit, sienllocdedemanarquehihagi d primersnomésdemanemquen’hihagi2, aleshoreselconjuntcorresponentcontéinﬁnitsenters.

12LahipòtesiH

HompotgeneralitzardemaneranaturallaconjecturadeDicksonprenentpolinomisirreductiblesambcoeﬁcientsentersqualssevol(enllocdelspolinomisde grau1delaforma x + a del’enunciat),cosaques’anomenatambéla hipòtesiH deSchinzel (amblaversióexplícitadeBatemaniHorn).

Conjectura 12 1 (HipòtesiH). Siguin f1(x),...,fm(x) ∈ Z[x] polinomisirreductiblesambcoeficientsentersicoeficientdegraumàximpositiu.Suposem quenohihacapnúmeroprimer p talque p divideixi f1(n) fm(n) pera tot n ∈ Z (anomenadalacondiciódeBunyakovsky).Aleshoreshihainfinits númerosenters n talsque fi(n) ésprimerperatot i = 1,...,m. Mésencara,tenimque

|{1 ≤ n ≤ x : fi(n) ésprimerperatot i ∈{1,...,m}}|∼ C D x logm(x) ,

on C i D sónlesconstantsexplícitessegüents; D éselproductedelsgrausdels polinomis fi(x),i C := p 1 N(p) p (1 1 p )m , on N(p) denotaelnombredesolucionsmòdul p de

=1 fj (n) ≡ 0 (mod p), i p esmoudinsdelconjuntdenúmerosprimers.

Noéscompletamentevident,peròespotdemostrarfàcilmentquelacondiciódeBunyakovskyimplicajustamentquelaconstant C ésestrictament positiva.ObserveuquesinoescompleixlacondiciódeBunyakovsky,aleshores hihaalgunprimer p talque N(p) = p,i,pertant, C = 0jaqueésunproducte (inﬁnit)onundelstermesval0.

Elcasméssimpledetots,quannoméshihaunpolinomi(osigui, m = 1), ielseugraués1(osigui, D = 1),ésdefeteldelteoremadeDirichletque veuremtotseguit.Enefecte,si f(x) = ax + b,amb a i b ∈ Z,lacondició deBunyakovskyesdevélacondicióqueelmàximcomúdivisorde a i b és1 (sónprimersentreells).Elsprimersquesóndelaforma f(x) pera x ∈ Z són elsprimerscongruentsamb b mòdul a.Finalment, N(p) ésiguala1si p no divideix a,iiguala0si p divideix a.ElteoremadeDirichletvaserlaprimera aplicacióprofundadelestècniquesanalítiquesperademostrarunresultat aritmètic.

Teorema 12 2 (Dirichlet). Siguin a> 1 i b ∈ Z entersprimersentreells.

Aleshores

{1 ≤ n ≤ x : an + b ésprimer}∼ p|a 1 1 p 1 x log(x) , onelproducteéssobreelsprimersdiferentsquedivideixen a.Equivalentment, enlasevaformaméshabitual,

{1 ≤ n ≤ x : n ésprimeri n ≡ b(mod a)}= 1 ϕ(a) x log(x) , on ϕ denotalafunciód’Euler.

Recordemquelafunciód’Euler

ϕ(a) = {m :1 ≤ m ≤ a i a i m sóncoprimers} compleixlafórmuladelproducte

ϕ(a) = a p|a 1 1 p , cosaquedemostral’equivalènciadelteoremadeDirichletperunsimplecanvi d’escala.

Voldriamencionarquehihaunaversiód’aquestaconjecturaencaramés generalpertald’incloureelcasdemésd’unavariable,itambéperaincloure conjecturescomladeGoldbach.

AquestaversióinclouconjecturescomladeSophieGermainqueafirma quehihainfinitsparellsdeprimers p i2p + 1(unresultatnoprovatperara), l’afirmacióquehihainfinitsprimersensuccessióaritmèticadellargada d fixada(elresultatdeGreeniTaoquehemexplicataladarrerasecció),oaltres resultatsquelesgeneralitzen,comelsdeTaoiZieglerquejahemcomentat,i tambémoltesdelesconjecturesquehemposatalasecció5.

Perexemple,lahipòtesiHquan m = 1,inoméstenimunpolinomi,inclouel casdelsprimersvoraquadrats(osigui,delaforma n2 + 1),peròtambémolts d’altres.Observeuquenohihaprimersdelaforma n2 1(aexcepciódel3), jaque n2 1 = (n 1)(n + 1) noésirreductible,inopotserprimerexcepte si n 1 = 1.Tampochihainﬁnitsprimersdelaforma n2 + n + 2,totiser irreductible,jaque2sempredivideix n2 + n + 2.

13ElteoremadeZhang

Retornemal’últimresultatdemostratrelatiuaaquestesconjectures,enquèes provalaconjecturadeDePolignacperaalgunvalorde n parell«petit»(inferior a70milionsenprimerainstància,inferiora246recentment).Reescriurem aquestteoremadelamanerasegüent,potsermésentenedora.

Teorema 13 1 Hihaunaconstant K (K = 70000000 peraZhang, K = 246 peraMaynardiPolymath)demaneraquehihainﬁnitsprimers p talsqueel primersegüent q compleix q ≤ p + K.

AquestteoremavaserdemostratperYitangZhangel2013(vaseranunciat el17d’abrildel2013).Aquestmatemàtictéunahistòriacertamentexcepcional. Nascutl’any1955alaXina,vaanaraferlatesialsEstatsUnitsd’Amèrica, concretamentalaUniversitatdePurdue,l’any1985(anyenquèvapublicar elseuprimerarticlebasatenresultatsdelseutreballdemàsteralaXina). Desprésdesetanysvaﬁnalitzarlatesiinovapodertrobarfeinadematemàtic. Vahaverdetreballarenunrestaurantdemenjarràpid,ﬁnsitotdormintal cotxe.FinalmentvatrobarfeinadeprofessorajudantalaUniversitatdeNew Hampshire.Quanvaferelseuanuncil’any2013nomésteniadosarticles publicats,elsegonl’any2001,iteniacinquanta-vuitanys.

ElqueésméssorprenentésquelademostraciódeZhangnoeraunaidea novaitotalmentrevolucionària,sinóqueeraunamilloramolttècnicaimolt ﬁnadelsúltimsresultatsenelcamp,elsqualsZhangvaentendrealaperfecció. Osiguique,totinopublicarres,haviaestatllegintientenentendetallelque s’estavafentpertaldepoderutilitzar-hoimillorar-ho.Totiaixò,lasevamillora aconseguiaunfetfonamentaliqueﬁnsaleshoresescreiaforadel’abast:poder provarl’existènciad’unaconstant K comladel’enunciatdelseuteorema.Fins aleshoreselsresultatsobtingutserenambunafunció K depenentdelamida delprimer p

UnaltrefetexcepcionaldelademostraciódeZhangésqueestavaperfectamenticlaramentredactada,iqueellmateixlavapoderexplicardetalladament davantd’experts.Aixòvaprovocarqueunmesdesprésdel’anuncil’article[20] jaestiguésacceptatenunadelesrevistesmésimportantsdematemàtiques: AnnalsofMathematics.

Uncopvaaparèixerl’articleesvaposarenmarxaunequipenlíniaper aportarlestècniquesquehaviaintroduïtallímitpertalderebaixarelvalordelaconstant K queZhanghaviaobtingut.Erenlavuitenaencarnació delprojectePolymath,unexperimentperaintentaraplicarlestècniquescollaborativesmassives,similarsalesdelsprojectesdecodiobertqueesdonen enelmóndelprogramari,almóndelamatemàticaacadèmica.Elsprojectes Polymath(http://polymathprojects.org/)funcionenapartird’unapropostadediversosexpertsd’unproblemaquecreuenqueespotintentarresoldre col.laborativament,queseguidamentesplantejaendetallalblogd’undels promotors.10 Ésenelscomentarisaaquestpostontothom(tutambépots!)va fentpropostes,posantresultatsparcials,explicantidees.Elpromotordesprés varesumintelméssignificatiudelques’haditfinsaleshoresenunaltrepost,i aixífinsaarribaraunresultatprousatisfactori.Sis’hiarriba,aleshoress’escriu unarticlesignatsotaelpseudònimD.H.J.Polymath[16].

DesprésqueelprojectePolymathobtinguésenunprimermomentuna millorasubstancialdelaconstantobtingudaperZhang,JamesMaynard,un matemàticquehaviaacabatlatesirecentmententècniquesdegarbell(que 10QueenelcasdelPolymath8vaserT.Tao,quejahasortital’articlediversesvegades.

YitangZhang.

sónlestècniquesutilitzadesperZhangperademostrarelseuteorema)es vaadonarquepodiaredemostrarelteoremaapartirderesultatsprevisque Zhangnohaviaconsiderat.Aquestanovademostració,obtingudaelnovembre del2013,portavaaunamilloraconsiderabledelresultat(definsa K = 600), ifinsitotdelresultatmilloratdelPolymath.AixíqueelprojectePolymath8 vareiniciar-seutilitzantaralesnovesideesdeMaynardfinsaobtenirelvalor de K = 246.

Defet,elquedemostraZhang,idesprésreﬁnaMaynard,ésunteorema moltmésgeneralenladirecciódelaconjecturadelesènuplesprimeres.

Teorema 13.2 (Zhang,Maynard,Polymath). Existeixunenter k (k=3500000 peraZhang, k = 50 peraMaynardiPolymath)demaneraqueperatot patró (n1,...,nk) senseobstruccionshihainﬁnitsenters x ≥ 1 peralsquals comamínim 2 delsenters x + ni pera i = 1,...,k sónprimers.

Observeuquelaconjecturadelesènuplesprimeresaﬁrmariaquepera tot k hihainﬁnitsenters x talsquehihacomamínim k primersentreels enters x + ni pera i = 1,...,k.

Perapoderdeduirelteorema13.1apartird’aquestsolscaltrobarquina éslaconstel laciódeprimersméspetitaambdiàmetre k.Iresultaquelamés petitapera k = 50vade0a246,iunaés11

Hompodriapensarquearajaésunaqüestiótècnicaarribaramillorarel teorema13.1finsaobtenirelvalorde K = 2,cosaqueensdonarialaconjectura delsprimersbessons(iambquasitotaseguretat,ladeDePolignac,finsitotla quantitativa,ialtresconjecturesmésgenerals).Però,defet,hihaunadificultat profundaenelsmètodesutilitzats,comhiésenelsresultatsdeChenoenels deVinogradov.Elsexpertsl’anomenenla barreradelaparitat,i,perexemple, enelcasqueensocupa,fariaquecomamoltespuguiobtenirelvalorde K = 6, quecorresponalvalor k = 3enelteoremaanterior.Elproblemadelaparitat implicaenelnostrecasqueelsmètodesactualsnopodendistingir k = 3 i k = 2.

14Conspiracionsaparents

L’11demarçdel2016,dosexpertsenprimersforçaconeguts,R.J.Lemke OliveriK.Soundararajan,varenferpúblicalservidor arxiv unarticleenquè mostravendadesnumèriquesaparentmentsorprenentsdebiaixosinesperats enladistribuciódelsnúmerosprimers[14].Perexemple,varencomprovarque 11Non’hihatansolsunad’aquestallargada!

detotselsprimersacabatsen1(enbase10)ﬁnsacentmilions,elprimerqueel segueixacabaen3perauns7milionsimig,unnombresimilaracabaen7,però solsuns5milionsimigacabenen9iuns4milionsimigacabenen1.Elmateix fenomenpassaamblesaltresterminacions,idefetentoteslesbases.Ditd’una altramanera,totiqueelteoremadeDirichletensdiuquelaprobabilitatque unprimeracabien1,en3,en7oen9éslamateixa,ellsvarencomprovar quesiunprimeracabaen1ésmoltmésprobablequeelsegüentprimeracabi en3(oen7,oen9)queen1.

Anteriormentjas’havientrobatd’altresbiaixossorprenents,totiqueno tanespectaculars,coml’anomenat biaixdeTxebixev:simiremlaquantitat deprimersinferiorsaunenter x,peralamajoriade x hihamésprimers congruentsamb3mòdul4quecongruentsamb1mòdul4(mireu[8]perauna introducciómoltdetalladaiaccessiblealfenomen).Elmateixpassaquanes comptenelsprimerssegonselseuvalormòdul3,odemanerasimilaramb qualsevolaltremòdul:ﬁxatunenter n,normalment12 hihamenysprimersﬁns a x quesónquadratsmòdul n quenoquenohosón.

Enunaprimerainstànciahompodriapensarqueaquestsfenòmensrevelenunaconspiracióquerebatrialanaturalesapseudoaleatòriadelsnúmeros primers.Peròelsmateixosautorsdemostrenenl’article[14]queaixònoés cert:defet,elmodelaleatoriquehempresentatanteriormentprediuaquest comportament,ﬁnsitotnumèricamentiambmoltbonaaproximació.Encara més,elsmateixosautorsexpliquenquevarentenirlaidead’estudiaraquest comportamentenescoltarunaconferènciasobreunfenomenmoltbenconegut enprobabilitat.Elqueelsvasorprendreésquefostanevidentnumèricament.

Elproblemadeprobabilitatqueelsvamotivaréselsegüent.Tenimdues persones, X i Y ,quejuguenaljocsegüent:cadascúvatirantunamoneda (perfecta)ﬁnsquesurtiobéunacaraidesprésunacreupera X,obéduescares seguidespera Y .Elprimerqueobtinguielquebusca,guanya.Donatqueun cophasortitunacara,latiradasegüentobésurtcaraobécreuamblamateixa probabilitat,hompodriapensarqueelsdostenenlamateixaprobabilitatde guanyar.Peròaixòésincorrecte!Resultaque X trigaràdemitjanaunes4tirades aobtenirelquebusca,mentreque Y necessitaràdemitjana6tirades.Podeu jugarunaestonaacasapertaldeveureelfenomenenacció,obémirarde fer-neelscàlculsprecisosvosaltresmateixos.

Enresum:ﬁnsara,totiladescobertadenouscomportamentsdetectats experimentalmentsobreladistribuciódelsnúmerosprimers,queenuna primerainstànciasemblavenindicarunpossibleerrorenelsmodelsaleatoris delsprimers,alﬁnalresultaqueespodenentendrejustamentgràciesala sevanaturalesaaleatòria,ielsfenòmensespodencomprovarutilitzantidees provinentsdelateoriadelaprobabilitat.Potserelfetqueenprimerainstància enssorprenguialsquetreballemenaritmèticadeuserperlanostraescassa intuïcióprobabilista.

12 Perònosempre.Defet,unargumentdegutaLittlewooddemostraquehihainﬁnitsvalors de x peralsqualsaixònoéscert.

15Sabernoésnoméstenir-neunademostració

Enaquestarticlehevolgutreﬂexionar,ambunexemplepràctic,sobreles preguntessegüents:quinsentittétenirunateoriamatemàticaconjectural? Contéinformaciórealmentútilperaunmatemàtic?Són,defet,matemàtiques?

Noconecendetalllasituacióencampsdelamatemàticadiferentsde l’aritmètica,entesaenunsentitmoltampli,onsédelcertquedurantels darrerscentanyshanaparegutunapiladeteoriesconjecturalsquehanserviti serveixendeguiaperamoltsdelsdesenvolupamentsiresultatsmésimportants. Perexemple,lesdiversesteoriesqueespeculensobrelesanalogiesentrecossos denúmerosicossosdefuncionssobreuncosﬁnit,subjacentstantenl’esquema delaprovadelesconjecturesdeWeilperWeiliGrothendieck,comﬁnsitoten lateoriarecentdelsperfectoidesdeScholze.Olateoria(oteories)delsmotius deGrothendieck(vegeu[15]peraunaintroduccióbreualaideasubjacent alateoriadelsmotius).13 OenelprogramagrandiósdeLanglands(podeu consultarl’articledeGelbart[7],que,totiserdefaunsquantsanys,ésuna bonaintroduccióaalgunesdelessevesidees,oelsdosvolumsdel12èSeminari deTeoriadeNombresdeBarcelona(UB-UAB-UPC)[1]peraunaintroducciómolt mésdetallada).Totesaquestesteoriesestancompletamentinterrelacionades,i hihaunmarcquelesengloba.Defet,lesformulacionsrecentsdelprograma deLanglandsutilitzenlateoriaconjecturaldelsmotius.

AlexanderGrothendieckiRobertLanglands.

Aquestesteoriesconjecturalssónútilsenmoltssentits.Primer,demanera pràctica,permetenrespondreconjecturalmentmoltespreguntesi,pertant, preveurequinpotserelresultatbuscatpertaldedesprésintentardemostrarlo«correctament».Nonomésaixò,tambépodenservirdeguiaenl’obtenció d’aquestademostració.D’algunamanerasónunpatró,talcomhosónalgunes

13EnelmateixvolumhihaunabiograﬁamoltdetalladadelavidaagitadadeGrothendieck.

partsdelafísicaperacertscampsdelesmatemàtiques.Peròperamil’objectiu mésimportantdelesteorieséseld’explicarresultatsconegutsiconjectures prèvies,queensportinaunacomprensiómésprofundadelsproblemesiens mostrinunaexplicaciódelesrelacionsaparentsentreresultatsdistintsia vegadesmoltallunyatsentreells.

Ésaquestdarrermotiularaóprofundadel’existènciadelesdiverses teories.Alcapialafi,elsmatemàticsnonomésvolemsercapaçosdefer càlculsmoltdifícils—comsovintelsnomatemàticscreuen—odedemostraro estudiardeterminatsresultats—comsovintensdemanendesd’altresciències,i seguramentésl’únicpelquese’nsavaluarà.Tambévolemcomprendre,cadacop ambmésprofunditat,larealitat(matemàtica),comhovolunfísic,oqualsevol altrecientífic.Iésenaquestsentitquelesexplicacionsdonadesperlesteories conjecturalspodenarribarasermoltméssatisfactòriesifinsitotmésútils, totinosercompletamentexactesonoestarformalmentdemostrades,queels resultatsestablertspursidurs.

Agraïments

VullagrairaW.Pitschhaver-meproposatferlalliçóinauguralqueemvainduir ﬁnalmentaescriurel’article,aF.BarsiaE.Nartlesinnumerablesconverses sobrearitmèticadurantmoltsanys,aJ.Verderalesnombrosescorreccions,ia M.Masdeulesconversessobrealgunsdelprotagonistesdel’articleicomentaris fetsaunaprimeraversiódel’article.IaC.Balaguertantescosesquenopucni enumerar.

Referències

[1] Bayer,P.;Travesa,A.(ed.).«Representacionsautomorfesde GL(2)». NotesdelSeminarideTeoriadeNombres(UB-UAB-UPC),2i3(1997).

[2] Chen,J.R. «Ontherepresentationofalargerevenintegerasthesumof aprimeandtheproductofatmosttwoprimes». Sci.Sinica,16(1973), 157–176.

[3] Chen,J.R. «Onthedistributionofalmostprimesinaninterval». Sci.Sinica, 18(5)(1975),611–627.

[4] delaValléePoussin,Ch.-J. Recherchesanalytiquessurlathéoriedes nombrespremiers.Brussel.les:Hayez,AcadémieRoyaledeBelgique,1897.

[5] dePolignac,A. Recherchesnouvellessurlesnombrespremiers.París: Bachelier,1851.

[6] Euclides. TheElements,circa300ac.

[7] Gelbart,S. «AnelementaryintroductiontotheLanglandsprogram». Bull. Amer.Math.Soc.(N.S.),10(2)(1984),177–219.

[8] Granville,A.;Martin,G. «Primenumberraces». Amer.Math.Monthly, 113(1)(2006),1–33.

[9] Green,B.;Tao,T. «Theprimescontainarbitrarilylongarithmeticprogressions». Ann.ofMath.(2),167(2)(2008),481–547.

[10] Guàrdia,J.;Jiménez,J.(ed.).«Mètodesdegarbell». NotesdelSeminaride TeoriadeNombres(UB-UAB-UPC),13(2005).

[11] Hadamard,J. «Surladistributiondeszérosdelafonction ζ(s) etses conséquencesarithmétiques». Bull.Soc.Math.France,24(1896),199–220.

[12] Hardy,G.H.;Littlewood,J.E. «Someproblemsof‘Partitionumerorum’; III:Ontheexpressionofanumberasasumofprimes». ActaMath.,44(1) (1923),1–70.

[13] Iwaniec,H. «Almost-primesrepresentedbyquadraticpolynomials». Invent.Math.,47(2)(1978),171–188.

[14] LemkeOliver,R.J.;Soundararajan,K. «Unexpectedbiasesinthedistributionofconsecutiveprimes». Proc.Natl.Acad.Sci.USA,113(31)(2016), E4446–E4454.

[15] Mazur,B. «Whatis...amotive?». NoticesAmer.Math.Soc.,51(10)(2004), 1214–1216.

[16] Polymath,D.H.J. «VariantsoftheSelbergsieve,andboundedintervals containingmanyprimes». Res.Math.Sci.,1(2014),art.12,83p.

[17] Quer,J. «Lafunció ζ deRiemann». ButlletídelaSocietatCatalanade Matemàtiques,22(2)(2007),197–228.

[18] Tao,T.;Ziegler,T. «Theprimescontainarbitrarilylongpolynomial progressions». ActaMath.,201(2)(2008),213–305.

[19] Vinogradow,I.M. «Representationofanoddnumberasasumofthree primes». Dokl.Akad.NaukSSSR,15(1937),169–172.

[20] Zhang,Y. «Boundedgapsbetweenprimes». Ann.ofMath.(2),179(3) (2014),1121–1174.

DepartamentdeMatemàtiques

UniversitatAutònomadeBarcelona

08193 Bellaterra,Barcelona,Catalonia xarles@mat.uab.cat

ButlletídelaSocietatCatalanadeMatemàtiques Vol.33,núm.1,2018.Pàg.81–82

Englishsummaries

P.Arias,C.Ballester,B.Coll,J.M.MazónandE.Provenzi

ThecontributionofVicentCasellestotheworldofmathematicsanditsapplicationtoimageprocessing

InthispaperwereviewthemostimportantcontributionsofVicentCasellesto thefieldofmathematicsandtheirapplicationtotheimageprocessingfield. Thecontributionscoverabroadpanoramaranging,frombasicresearchasis thecaseofhiscontributionstothefieldofnon-linearEDPsandtheanalytical studyofthetotalvariation(TV)modeltothesphereoftheapplicationsinthe fieldofimageprocessing.Tosomedegree,thesectionsrelatetotheareasin whichtheparticipationwasmostsignificant;specifically,tothesphereofbasic researchpart,thecontributionstothestudyofthefunctionoftotalvariation, stronglydegeneratequasilinearequationsandchockedflowequations.With regardtoapplicationsinthefieldofimageprocessing,wehavechosenthree topicsinwhichCasellescontributedinaverysignificantway:thedetectionof contours,theproblemofinterpolationor“inpainting”andthemathematical formulationofcolortheory.

Keywords: functionalanalysis,totalvariation,non-linearPDEs,imageprocessing,contourdetection,inpainting,colortheory.

MSC2010SubjectClassiﬁcation: 68T99,46Txx,35K93.

JoanCarlesNaranjo

PonceletinSaratovprison

PonceletwasasoldierintheFrencharmywhotookpartintheBattleofKrasnoï wheretheNapoleonictroopsweredefeatedintheRussianwar.Duringhisstay

asaprisonerinSaratov,basedonhisrecollectionoftheinspiringlecturesof GaspardMongeattheÉcolePolytechnique,heworkedonthefoundationsof projectivegeometry.TheinﬂuenceoftheworkofPonceletextendsthroughout the19thcentury.AmongtheresultsprovedbyPonceletinthisperiodthe mostremarkableistheacclaimed“Poncelet’sporism”whichdealswiththe existenceofpolygonswithverticesinagivenconicandedgesthataretangents toanotherﬁxedconic.InthispaperwereviewcertainfactsofPoncelet’slife andwesetoutanotionofoneofthedemonstrationsoftheporism.

Keywords: projectivegeometry,conics,Poncelet’sporism.

MSC2010SubjectClassiﬁcation: 01A55,14N05,14N15.

XavierXarles

Primesunveiled

Themainaimofthispaperistopresentinaninformalwayaprobabilisticpoint ofviewonthedistributionofprimesthatcouldexplainwhysomewell-known conjecturesontheprimesaretrue.Wealsopresentsomeresultsshowingthat thisapproachreallycapturestheactualdistribution.Atthesametime,we introducesomeofthemostrecentresultsonprimesbyGreen,Tao,Zhang, MaynardandPolymath.

Keywords: primes,zetafunction,primetuples,pseudorandom,Goldbach’s conjecture,DePolignac’sconjecture,Zhang’stheorem.

MSC2010SubjectClassiﬁcation: 11-02,11A41,11P32.

Instruccionsperalsautors

Elsarticlessotmesosapublicaciós’hand’enviaralseditorsoaqualsevol membredelcomitèeditorial,percorreuelectrònic,preferentmentenformat PDF.Elsoriginalshandecontenirlaversióanglesadeltítol,unresumbreuen catalàienanglès,paraulesclauencatalàienanglèsielscodisdelaclassiﬁcació permatèriesMSC2010.

Lesversionsdeﬁnitivesdelsarticlesacceptatss’handepresentarencodiTEX,preferentmentenl’estilLATEXpropidel Butlletí.Aquestestilespot obteniralespàgineswebdelaSocietatCatalanadeMatemàtiques(SCM).Fem notarqueenaquestapublicaciós’utilitzapreferentmentelpuntperaseparardecimals,enllocdelacomarecomanadaperl’IEC,perpoderfacilitarla comprensiódelesexpressionsmatemàtiques.Pertald’accelerarelprocésde producció,espregaalsautorsquesegueixinlesindicacionscontingudesenel documentd’exemple.

Laversióenpaperdel Butlletí s’imprimeixenblancinegre.Quanun articlecontinguifiguresencoloriesconsidericonvenient,l’autorproporcionarà unaversiódelsgràficssubstituintelcolorpertonsdegrisosilíniesdegruix variable.Aixímateixmodificaràelscomentarisquefacinreferènciaalcolorde lesfigures.Enqualsevolcasel Butlletí publicaràl’originalencolorenelseu formatelectrònic.

Elsautorsdelsarticlespublicatsal Butlletí enreteneneldretdecòpia (copyright)iautoritzenl’IECadifondre’ls,tantatravésdelapublicacióimpresa commitjançantelsportalsdigitalspropisod’altresambquès’estableixinels convenisoportunsaaquestefecte.Ésresponsabilitatdelsautorsassegurar queesdisposadelsdretsdereproducciódelsgràﬁcsidelesﬁguresquehi apareguin.CadaautorrebràunacòpiaenPDFd’altaqualitatdelaversiódigital delseuarticleiunexemplarimprèsdelnúmerodel Butlletí enelquales publiqui.

Lacorrespondènciaadministrativarelacionadaambel Butlletí s’had’adreçaral’SCM.

Comitèeditorial

JuliàCufí(editorencap) DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona jcuﬁ@mat.uab.cat

BartomeuColl

Dep.deMatemàtiquesiInformàtica UniversitatdelesIllesBalears tomeu.coll@uib.cat

NúriaFagella

Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona fagella@maia.ub.es

ArmengolGasull

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona gasull@mat.uab.cat

AntoniGuillamon DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya antoni.guillamon@upc.edu

GáborLugosi

ICREAiDepartamentd’Economia UniversitatPompeuFabra gabor.lugosi@upf.edu

RosaCamps(editoraadjunta)

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona rcamps@mat.uab.cat

MarcNoy

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya marc.noy@upc.edu

FrancescPlanas

DepartamentdeMatemàtiques UniversitatPolitècnicadeCatalunya francesc.planas@upc.edu

AgustíReventós

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona agusti@mat.uab.cat

JoanSaldaña

Dep.d’Informàtica,Mat.AplicadaiEstadística UniversitatdeGirona joan.saldana@udg.edu

MartaSanz-Solé Dep.deMatemàtiquesiInformàtica UniversitatdeBarcelona marta.sanz@ub.edu

SocietatCatalanadeMatemàtiques

La SocietatCatalanadeMatemàtiques(SCM) ésunasocietatﬁlialdel’Institutd’EstudisCatalans,quecontinualesactivitatsdelaSecciódeMatemàtiques delaSocietatCatalanadeCiències,quefoufundadaperl’Institutl’any1931. Lesﬁnalitatsdel’SCM són:elconreudelesciènciesmatemàtiques,l’extensió delseuconeixementenlasocietatcatalana,elfomentdelseuensenyament idelasevainvestigacióteòricaiaplicada,aixícomlapublicaciódetotamena detreballsques’adeqüinaaquestsobjectius.L’SCM desenvolupalesseves activitatsenlesterresdellenguaiculturacatalanes.Elcatalàés,doncs,la llenguapròpiadel’SCM ilaqueésusadanormalmententotselsseusactesi publicacions.

L’SCM editalespublicacionsperiòdiques SCM/Notícies i ButlletídelaSocietat CatalanadeMatemàtiques.Elssocisdel’SCM reben,gratuïtament,aquestes duespublicacions.

L’SCM téconvenisdereciprocitatambdiversessocietatsmatemàtiquesd’arreudelmón,mitjançantelsqualselssocisdel’SCM obtenenunareduccióenla quotadesocid’aquestessocietats.Aixímateix,elssocisdel’SCM podenfer-se socisdelaSocietatMatemàticaEuropeapagantunaquotacomplementària.

LaJuntaDirectivadel’SCM estàconstituïdaperlespersonessegüents:

President:XavierJarqueiRibera

Vicepresident:EnricVenturaiCapell

Adjuntadelavicepresidència:IolandaGuevaraiCasanova

Secretari:AlbertRuiziCirera

Tresorera:NatàliaCastellanaiVila

Vocals:AlbertAvinyóiAndrés,MartaBeriniiLópez-Lara,Abraham delaFuentePérez,NúriaFagellaiRabionet,JosepGranéiManlleu, CarlesRomeroiChesa,ManelUdinaiAbelló Delegatdel’IEC:PilarBayeriIsant

L’adreçadel’SCM éscarrerdelCarme,47,08001Barcelona.Telèfon:933 248583.Fax:932701180.Correuelectrònic: scm@iec.cat.Adreçaweb: http://scm.iec.cat.