BSCM, 30-2

BUTLLETÍ

DE LA SOCIETAT CATALANA DE MATEMÀTIQUES

Institut d’Estudis Catalans

índex

q Joaquim Bruna

Aproximació no lineal i mostratge comprimit

q Pilar Guerrero i Tomás Alarcón

109

Models estocàstics d’escales múltiples per la dinàmica de poblacions cel·lulars: mètodes asimptòtics i numèrics 125

q Timothy G. Myers i Sarah L. Mitchell

Una anàlisi matemàtica del moviment d’una pilota de futbol durant el vol 169

q Joaquim Ortega-Cerdà

Sèries de potències (aleatòries) 195

q English summaries 209

Volum 30 • Número 2 • Any 2015

BUTLLETÍ

DE LA SOCIETAT CATALANA DE MATEMÀTIQUES

Institut d’Estudis Catalans

Volum 30 ● Número 2 ● Desembre 2015

©delsautorsdelsarticles

EditatperlaSocietatCatalanadeMatemàtiques filialdel’Institutd’EstudisCatalans CarrerdelCarme,47 08001Barcelona

Textrevisatlingüísticament perlaUnitatdeCorrecciódelServeiEditorialdel’IEC.

ImprèsaLimpergraf,SL

ISSN:0214-316-X DipòsitLegal:B.19272-1987

Sónrigorosamentprohibides,sensel’autoritzacióescritadelstitularsdel copyright,lareproducciótotaloparciald’aquestaobraperqualsevolprocedimentisuport,incloent-hilareprografia ieltractamentinformàtic,ladistribuciód’exemplarsmitjançantllogueroprésteccomercial,la inclusiótotaloparcialenbasesdedadesilaconsultaatravésdexarxatelemàticaod’Internet. Lesinfraccionsd’aquestsdretsestansotmesesalessancionsestablertesperleslleis.

ButlletídelaSocietatCatalanadeMatemàtiques Vol.30,núm.2,2015

Índex

JoaquimBruna Aproximaciónolinealimostratgecomprimit....................................109 PilarGuerreroiTomásAlarcón

Modelsestocàsticsmultiescaladeladinàmicadepoblacionscel.lulars: mètodesasimptòticsinumèrics..................................................125

TimothyG.MyersiSarahL.Mitchell Unaanàlisimatemàticadelmovimentd’unapilotadefutboldurantelvol.....167

JoaquimOrtega-Cerdà Sèriesdepotències(aleatòries)....................................................193

Englishsummaries.....................................................................207

ButlletídelaSocietatCatalanadeMatemàtiques Vol.30,núm.2,2015.Pàg.109–123. DOI:10.2436/20.2002.01.60

Aproximaciónolinealimostratgecomprimit

JoaquimBruna

Resum: Enaquestarticledonemunapinzelladaauncamprelativamentnoudela matemàtica,el mostratgecomprimit,untermequecorresponal’expressió compressed sensing o compressivesampling.Ésunabrancadeltractamentdelsenyalqued’alguna manerahaaparegutdeformanaturalassociadaaunaltregrancampbenmoderni present,l’anomenat bigdataanalysis.Elmostratgecompressiunotractapasdela manipulaciódegransbasesdedadesperextreure’ninformacióútil,sinójustamentde nogenerarinformacióinútil,innecessària.Peral’exposició,ensreferirembreumenta unaaltrateoriaquetéentitatpersisola,la teoriadel’aproximaciónolineal.

Paraulesclau: discretització,aproximaciólineal,aproximaciónolineal,baseshilbertianes,mostratgecomprimit,vectorsrars,descodificadors,matriusaleatòries,bases incoherents.

ClassificacióMSC2010: 94A12,68P30,41A46.

1Analògic vs. digital

Lesmatemàtiquessovintutilitzenenelsseusmodelsperdescriureelmón funcionsanalògiques f(t), f(x), t,x ∈ I,on I designaaquíuninterval,acotat ono.Elsmodelsteòricssuposenque x o t ésunavariableindependentque potprendretotselsvalorsde I,uncontinudevalors,ipodemveure f comun vectorquetéuncontinudecomponents.Comquelesmatemàtiquespretenen quantificarmagnituds,sesuposaenelsmodelsqueaquestesfuncionssón quantificablesenalgunsentit.Elméscomúésimposarquetenenenergiafinita, f = I |f(x)|2 dx 1 2 < ∞

ihomdiullavorsque f ∈ L2(I).Hemdeveureaquestaexpressiócomlaversió contínuadelanormaeuclidianaqueensésfamiliar,jaquenofemaltracosa AquestarticleésunaversiódesenvolupadadelalliçóinauguraldeMatemàtiquesdelcurs2013–2014alaUniversitatAutònomadeBarcelona,iesnodreixdelesreferències[7],[8]i[10].

quesumarelquadratdetoteslescomponents(infinites)delvector f .Així, L2(I) ésl’espaieuclidiàd’uncontinudedimensions,ilanormaensserveixper quantificarcomsóndeproperesduesfuncions,

f g = I |f(x) g(x)|2 dx 1 2

Quanparlemd’una digitalitzacióodiscretització de f ,ensreferimd’una formaimprecisaaquelcomquerepresentaoaproxima f peròquenodepèn d’uncontinudedimensions,sinód’unnombrefinito,comamolt,numerablede dimensions.Sovintaixòesformulaperafuncionsd’undeterminatsubespai E de L2(I).Perprecisar,aquídiremqueunadigitalització(ideal)de f ∈ E ⊂ L2(I) consisteixsenzillamentaexpressarelvector f enunabaseortonormal numerable(basehilbertiana) (ψn) de E.Aixòés

f = n f,ψn ψn, onelscoeficientssónlescorrelacions

f,ψn = I f(x)ψn(x)dx.

Lescorrelacions f,ψn constitueixenuna digitalització de f . Elconceptede baseortonormal és,pertant,elmateixqueelde basecartesianadel’espaieuclidià.Elsvectors ψn sónunitarisiperpendicularsdosados, ψn,ψm = 0,si n = m,ihomtéelteoremadePitàgores

f 2 = n | f,ψn |2 ,

queenaquestcontexts’anomena teoremadeParseval

L’exemplehistòricamentmésimportantéslabasedeFourierdesinusi cosinuso,siesvol,d’exponencialscomplexes.Si I = [ a,a] ésuninterval acotat,labasedeFourierde L2(I) consisteixenlesexponencialscomplexes 1 √2a e π a int ,n ∈ Z.

EldesenvolupamentensèriedeFourierprenlaforma f(t) = n cne π a int ,

ambcoeficients

cn = 1 2a a a f(t)e π a int ,

ques’anomenen coeficientsdeFourier.Evidentment,totafunció f ∈ L2(I) s’identificaambunafunció2a-periòdica,demaneraqueeldesenvolupament anteriorveadirquetotafunció2a-periòdicaésunasuperposició,ésadir, unasuma,delesfuncions2a-periòdiquesméselementals,quesón cos( π a nt), sin( π a nt), n ∈ N

UnaltreexempleparadigmàticéselconegutteoremadeShannon-WhittakerKotolnikov.Sigui E laclassedefuncions f ∈ L2(R) ques’obtenencoma superposiciódesinusicosinusdefreqüències ω,amb ω ≤ a,

f(x) = |ω|≤a g(ω)e2π iωx dω, amb g ∈ L2(R).

Aquestessónlesfuncionsde bandalimitada,ambampladadebanda a.Llavors

f(x) = n f n 2a ψn(x), on ψn(x) = sin π(2ax n) π(2ax n) .

Lesfuncions ψn,quesóntraslladadesireescaladesdelafunciósinuscardinal sin πx πx ,formenunabaseortonormalde E;enaquestcas,lescorrelacions f,ψn coincideixenambelsvalors f( n 2a ) i 1 2a s’anomena elpasdeNyquist.Matemàticament,aquestresultatésequivalentalquehemcomentat,en elsentitquetotafuncióde L2(I) espotescriurecomlasumad’unasèriede Fourier.

Si,amés, f tinguéssuporten [ T,T],aixòsignificariaquedepènd’aproximadament4Ta paràmetres.Llevatdelcasque f = 0,nohihafuncionsde bandalimitadaambsuportcompacte,perquètotafunciódebandalimitada téunaextensióentera;tanmateix,eltreballdeLandauiPollackmostraque l’espaidelssenyalsqueaproximadamenttenensuporttemporaldemida T i aproximadamentampladadebanda a tédimensióaproximadament4Ta,on, ésclar,calprecisarelsignificatencadacasdelterme aproximadament

Unaltreexemplemoltimportantdebasesidedigitalitzaciósónles basesd’ondetes.Enslimitaremaquíauncasespecial.Una ondetaambsuport compacte ésunafunció ψ ambsuportcompactedinsl’interval ( 1/2, 1/2), normalitzada,amblameravellosapropietatquelesversionsreescaladesi dilatades

ψk,m(x) = 2 k 2 ψ(2kx m),k,m ∈ Z formenunabasehilbertianade L2(R),ésadir, f = k,m f,ψk,m ψk,m, pera f ∈ L2(R).

Aquíhihaundobleíndex (k,m) ilescorrelacions f,ψk,m sónmitjanes ponderadesde f enl’intervaldiàdicdemida2 k centraten m 2k .

Veiemqueenlesondeteshihadosparàmetres,unparàmetredeposició m iunparàmetred’escala k.L’exempleméssenzillésl’ondetadeHaar,queés lafuncióqueval 1en [ 1 2 , 0] i1en [0, 1 2 ].L’existènciad’ondetesd’aquest tipus,que,amés,sónregulars,ésunfetmoltimportant,degutaDaubechies. Untercerexemplebenclàssicdebaseseldonenlesdiversesfamíliesde polinomis (pn), pn degrau n,queformenunabasehilbertianade L2(0, 1),o de L2(0, 1) ambunpes.ExemplesensónelspolinomisdeHermite,Laguerre,Jacobi,Gegenbauer,Chebyshev,Legendre,etc.CadaproblemadeSturm-Liouville portadeformanaturalaunabased’aquestescaracterístiques.

2Aproximaciólinealinolineal

Suposemquevolemaproximar f ambunainformaciódemida N utilitzantuna base (ψn)

f = n cnψn.

Unaformadefer-hoés,senzillament,mitjançantels N primerscoeficients

Notemqueaquestadefiniciópressuposaquelabase (ψn) estàordenadao jerarquitzadad’algunaforma.Perexemple,entermesdelafreqüènciaen labasedeFourier,lagrandàriadelsparàmetresdeposicióifreqüència,etc. Òbviament,enaquestcas,homté (f + g)N = f N + gN ,ésadir,l’aproximació éslineal.

Arabé,aixònoéselmillorquepodemfer.Siprenemelscoeficients cn que corresponenaunsubconjunt A delsnúmerosnaturalsiformem

tindrem

i,pertant,lamilloraproximacióde f utilitzant N coeficientsl’obtindrem ordenantdemésgranaméspetitenvalorabsolutelscoeficients cn (que tendeixenazeroquan n →∞)iquedant-nosambels N coeficientsmésgrans, elsméssignificatius.Així,definim

Aquestaésaraunaaproximacióadaptativaperònolineal: (f + g)N ≠ fN + gN . Ésnaturalpreguntar-secomsóndebonesaquestesaproximacions.Quantitativament:comdegranhemdeprendre N pertalquel’errorsiguiméspetit queunaquantitat ε prefixada?Aquestaqüestiós’estudiadelamanerasegüent: si E ésunadeterminadaclassedefuncions,comdecau f fN si f ∈ E? Típicament,voldríem,perexemple,quefos

f fN ≤ C f 1 N α ,

ambunvalorde α commésgranmillor.Aquestexponent α depèndela classe E idelabaseutilitzada (ψn)

Lesbasesd’ondetessónmoltimportantsenlesaplicacions.Elfetmatemàticquehoexplicaésque,peramoltesclasses E defuncions(particularment, lesquemodelitzenimatges),lesbasesd’ondetesdonenelmillorexponent α, demaneraque,amb N nogairegran,l’aproximacióde f per fN jaésproubona. Ditd’unaaltramanera,lesbasesd’ondetestenenlapropietatderepresentar acuradamentfuncionsd’interèspràcticambmoltpocscoeficientssignificatius,perquèlasevaexpressióexactatéunaexpressiórara, sparse,ambmolts coeficientsmoltpetits,enlesbasesd’ondetes.Aixòlesfaespecialmentútils, perexemple,al’horadecomprimirimatgesenlesnostrescàmeresdigitals. Entermesgenerals,siunaimatgeesrepresentaenunabased’ondetesde Daubechies(mésprecisament,enlasevaversióbidimensional),hihaaproximadament106 coeficients;siensquedemambelcincpercentdelscoeficients méssignificatius,fentzeroelsaltres,ifemlareconstruccióapartird’aquests coeficients,veuremunaimatgepràcticamentidèntica.

3Unnoupas:elmostratgecomprimit(compressedsensing o compressivesampling

)

Enlaseccióanterior,hemvistlautilitatdel’aproximaciónolinealenbases d’ondetes.Representadesenbasesd’ondetes,moltesfuncionsd’interèspràctic s’aproximenacuradamentdeformanolineal.

Peròreflexionemunamica.Homfal’esforçd’obtenirunmiliódecoeficients perdesprésnegligir-lospràcticamenttots.Noésgenseficientaixò!

Ésenaquestpuntonapareixlapreguntanatural,clau,iqueensportaràa unnouparadigma,eldel mostratgecomprimit:éspossibledissenyaralgunalgorismequeenspermetiobtenirdirectament fN nomésamb(aproximadament) N observacions?

Laresposta,sorprenent,éssí,iladónalateoriadelmostratgecomprimit. L’objectiud’aquestaseccióésexplicarenquinsentitaixòéscerti,sobretot,de quinamanera.Veuremcom,enlarespostaaaquestapregunta,escombinen nocionsd’àlgebralineal—potsernoexactamentdel’àlgebralinealestàndard— ambnocionsestocàstiquesmoltactuals,comaralesmatriusaleatòries.

Començaremformulantelproblemaenelmarcdel’àlgebralineal.

Tenimunvector f ∈ RD,on D ésenorme,perexemple,elnombredepíxels d’unaimatge.Podempensartambéque f ésunafunciódefinidaa {1, 2,...,D}. Tenimunaexpressióde f enunabaseortonormal

Suposemque f és N-rar enlabase Ψ ,ésadir,que f = fN (quevoldir que f tansolsté N coeficientsnonuls),obéqueés compressible,enelsentit

que f fN = X XN tendeixazeromoltràpidament.Unaobservació fonamentalatenirencompteperentendrelasituacióéslasegüent:sabem que f és N-rarenlabasedeles ψn (perexemple,perquè f ésunaimatgei labaseésunabased’ondetes),perònosabemquinssónels N-coeficientsno nuls(sihosabéssim,lasituaciófóratrivial,laresoldríemambl’àlgebralineal estàndard).

Modelitzemaraelmostreigde f ,lainformacióqueentenim,mitjançant unescorrelacionsambaltresfuncions φk linealmentindependents:

yk = f,φk ,k = 1,...,M, onelnombredemostresés M,quehemdepensarcomunnombremoltmés petitque D.Llavorslapreguntaés:podemrecuperar f apartirdels yk?Com que f = fN ,si f és N-rar,depènde N coeficients,elmillorquepodemesperar ésque M = N

4L’àlgebralinealdelsvectorsrars

Representem-hototentermesmatricials

Y = Φf = ΦΨ X = AX, on A : RD → RM i M D.

Lamatriu A = ΦΨ ,d’ordre M × D,s’anomena demostratge (sensingmatrix),i térang M.Llavorspretenemrecuperar X de Y = AX sabentque X és N-raro bécompressible.Posem ΣN perdesignarlaclassedelsvectors N-rarsde RD . Tenimmoltesmenysequacions, M,queincògnites, D,peròsabemquenomés N incògnitesnosónzero,sensesaber,però,quines. Engeneral,un descodificador ésunaaplicació

∆ : RM → RD

talque ∆AX = X si X ∈ ΣN .Undescodificadortriaperacada Y ∈ RM un vector ∆(Y) delavarietatlineal B(Y) ={Z : AZ = Y }

Undescodificadornoésnecessàriamentlineal,sibéaquísuposaremper simplificarque ∆0 = 0.Esvol,pertant,queundescodificadorsiguiuninvers perl’esquerrade A sobreelsvectorsrars.Perdefinició,sóninversosperla dretade A, A∆Y = Y .Notemquetrianten B(Y) elvector Z denormamínima s’obtéuninversperladreta,lineal,queprenvalorsenl’ortogonaldelnucli de A.

Volemque AX determini X pera X ∈ ΣN ,ésadir: X,X ∈ ΣN ,amb AX = AX had’implicar X = X ,obé,si X X ∈ ker(A),llavors X = X . Volem,pertant,que ker(A) ∩ Σ2N = 0.Defet,enaquestcas,podemdefinir undescodificador.Definimsenzillament ∆(Y) triantentretotselsvectors Z talsque AZ = Y unquetinguisuportmínim,ésadir,ambelmàximnombre decomponentsnul les.Llavors,si X és N-rar, ∆AX ésunvector Z talque AZ = AX quetésuportmínim,i,pertant,tambéés N-rar.Enconseqüència, X Z ∈ ker(A) ∩ Σ2N i Z = X

Definició 1 Associemacadamatriu A d’ordre M × D elnúmero s(A) definit comelméspetitnombredecolumnesde A quesónlinealmentdependents.És adir,qualssevol s(A) 1columnesde A sónsemprelinealmentindependents.

Adiferènciadelanocióde ranghabitual,elnúmero s(A) depènde A ino nomésdelsubespaiengendratperlescolumnesde A.Evidentment,homtéque s(A) ≤ rang(A) + 1.

Laigualtat ker(A) ∩ Σ2N = 0significaquenopodenhaver-himai2N columneslinealmentdependents,ésadir,quequalssevol2N columnesde A hande serlinealmentindependents,aixòés,2N ≤ s(A) 1.Així,homtéque Y = AX determina X ∈ ΣN ,siinoméssi s(A)> 2N.Ensinteressen,doncs,matriusque compleixinaquestacondició,que,talcomhemvist,ésequivalental’existència d’undescodificador ∆ querecuperi X ∈ ΣN de Y = AX.

Naturalment,aquestacondicióimplicaque2N ≤ rang(A) i,pertant,que 2N ≤ M.Fixats N, D, M amb M ≥ 2N,semprehihamatriusd’ordre M × D tals quequalssevol2N columnessiguinlinealmentindependents.Éssuficienttrobar D vectorsa R2N talsquequalssevol2N d’ellssiguinlinealmentindependents. Si0 <t1 <t2 < <tD sónarbitraris,lamatriuquetéentrada ti 1 j alafila i, columna j,tétotselsmenorsd’ordre2N×2N quesónmatriusdeVandermonde i,pertant,invertibles.Aquestesmatriussón,però,malcondicionadesi,per tant,noadequadesperalcàlculnumèric.

Arabé,pertalqueundescodificador ∆ tinguiinterèspràctic,hadeser robust,enelsentitquesi X ∉ ΣN però X XN éspetit,voldríemquetambé ∆AX fospropera X d’unaformacontrolada.Elmésnaturalésimposarque existeixiunaconstant C> 0talque

∆AX X ≤ C X XN , (1) que,naturalment,quantificaelfetque ∆AX = X,si X és N-rar. Òbviament,aixòimplica

X ≤ C X XN ,X ∈ ker(A), peraunacertaconstant C.Defet,implicaaquestamateixadesigualtat,però amb2N enllocde N (vegeu[8]):

X ≤ C X X2N ,X ∈ ker(A). (2)

Enefecte:donat X ∈ ker(A),consideremunadescomposicióde X2N endos vectors N-rars, X2N = X1 +X2,isigui X3 = X X2N .Comque X1 ∈ ΣN ,tindrem que X1 = ∆A( X1);comque X ∈ ker(A),tindremque A( X1) = A(X2 + X3); pertant, X1 = ∆A(X2 + X3).Aleshores,per(1),

X = X2 + X3 ∆A(X2 + X3) ≤ C (X2 + X3) (X2 + X3)N

Arabé,comque X2 és N-rar,ésclarqueladarreraexpressióésmenoroigual que X3 = X X2N

Quanescompleix (2),homdiuque A télapropietatNSP(nullspaceproperty) d’ordre 2N respectedelanormaeuclidiana.

Alapràctica,elsdescodificadorshandesertambérobustsrespectedels errors,perquèlesmostrespodencontenirsoroll.Nomesurarem Y = AX exactament,sinó

Y = AX + Z, on Z ésunerror,estocàsticodeterminista.Si ∆ ésundescodificador,diemque ésrobust si ∆(AX + Z) X ≤ C Z ,X ∈ ΣN ,Z ∈ RD . (3)

Anàlogamentalesaltrespropietats,aquestacondiciónatural—l’existència d’undescodificadorrobust—implicaunapropietatdelamatriu A,concretament

(4)

Perveure-ho,siguin X,Y ∈ ΣN idefinim Z = 1 2 A(X Y),demaneraque

AX Z = AY + Z = 1 2 A(X + Y).

Si W = ∆(AX Z) = ∆(AY + Z),(3)implica X Y ≤ X W + W Y ≤ 2C Z = C AX AY .

Fixem-nosque(4)implicaque X ∈ ΣN espotrecuperarde AX. Ladefiniciósegüentfouintroduïdaa[6]i[2].

Definició 2. Lamatriu A satisfàlapropietatRIP(restrictedisometryproperty) d’ordre N,sihiha δN petittalque (1 δN ) X 2 ≤ AX 2 ≤ (1 + δN ) X 2,X ∈ ΣN .

Significaquequalssevol N columnesde A sóngairebéortogonals.Pertant,si A satisfàlapropietatRIPd’ordre2N, A preservaaproximadamentladistància entredosvectors N-rars.

LapropietatRIPimplicaunaversiódelapropietatNSP,peròamblanorma L1.Lanorma L1 d’unvector X esdefineixcoma X 1 = D i=1 |xi|

Peraunvector X ∈ ΣN ,ladesigualtatdeSchwarzimplicaque X 1 ≤ √N X

Elresultatprecís,quenodemostrarem,ésquesi A télapropietatRIPd’ordre N ambunaconstant δN < √2 1, llavors X ≤ C X X2N 1 √N ,X ∈ ker(A), amb C = 2 1 (1+√2)δN

5Eldescodificadorbasatenlanorma L1

Reprenemlasituacióanterior.Tenim Y = AX,on A ésunamatriudemostratge M ×D amb M D.Tanmateix,pretenemrecuperar X ∈ RD de Y = AX ∈ RM utilitzantlainformacióque X és N-raro N-compressible.Alaseccióanterior, hemvistcondicionssobrelamatriu A quesónnecessàriespertalquepugui existirundescodificador ∆ quepermetiobtenir X de AX quan X ∈ ΣN d’una formaestableirobusta.Enaquestasecció,descriuremlasituaciópelquefaala suficiènciad’aquestescondicions,ésadir,alaconstrucciódedescodificadors concrets.Recordemquedefinirundescodificadorvoldirsimplementdefinirun criteripertaldeseleccionarperacada Y unvectordelavarietatlineal B(Y). Atèsqueelnostrepropòsitprincipalésrecuperarvectorsrars,elmés natural,allòquesemblamésintuïtiu,éstriarelmésrardelsvectorsde B(Y), ésadir,podemconsiderareldescodificador ∆0(Y) = Z,on Z éselvector Z ∈ B(Y) queminimitzielnombre Z 0 decomponentsnonul les.Sila matriu A ésinjectivasobreelsvectors N-rars,ésadir, s(A)> 2N,jahemvist que ∆AX = X,si X ∈ ΣN .Arabé,elproblemaambaquestdescodificadorés que Z 0 noésconvexilaimplementaciópràcticanoésfactible.Defet,s’ha demostratqueimplementar ∆0 enunordinadorés NP-hard,ésadir,d’una grancomplexitatdecàlcul.

HemvistquelapropietatNSPd’ordre2N,equivalental’equació (2),és necessàriaperal’existènciad’undescodificadorquecompleixi (1).Araveurem quetambééssuficient;vegeu[8].Enefecte,enaquestcas,triementretotsels vectors Z talsque AZ = Y aquellperalqual Z ZN ésmínim,ésadir,el quemillors’aproximapervectors N-rars.

Comque X Z estàenelnuclid’A,(2)implica X Z ≤ C X Z (X Z)2N .

Enaquestpunt,recordemque X2N éslamilloraproximacióde X amb2N coeficients;pertant,homté,engeneral, (U +V) (U +V)2N ≤ U UN + V VN . Ambaixò,l’expressióanteriorésmenoroigualque C( X XN + Z ZN ).

Perdefinició, Z ZN ≤ X XN i,pertant, X Z ≤ 2C X XN

Així,hemvistquelapropietatNSPd’ordre2N ésequivalental’existènciad’un descodificador ∆ quecompleixi (1).Comque XN és,perdefinició,lamillor aproximacióde X amb N coeficients,lapropietatNSPd’ordre2N ésequivalent alacondició

X ≤ C X XΓ ,X ∈ Ker(A), cardinal(Γ ) ≤ N. (5)

Aquí Γ ⊂{1, 2,...,N} ielvector XΓ éselques’obtéde X conservantles componentsquecorresponena Γ ifentzerolesaltres.

Arabé,veuremtotseguitqueaixòimplicaque M ≥ C 2D (c.f.[8]).Peral casqueelcardinalde Γ sigui1,(5)significaqueperatot j = 1,...,D homté

queimplica

i,pertant,

2 j ≤ (C

Aixòhauriadesercertperatot X enelnuclide A.Sigui e1,...,eD labase canònicade RD isigui v1,...,vD M unabaseortonormaldelnuclide A.Sigui P laprojeccióortogonalsobreelnuclide A.Llavors,pera X = P(ej ) obtenim P(ej ),ej 2 ≤ 1 1 C 2 ,

queéselmateixque

,...,D.

Sumantrespectede j obtenim D M = D M i=1 vi 2 ≤ D 1 1 C 2 ,

ésadir, M ≥ C 2D. Aquestésunresultat negatiu,jaqueensindicaque M hadeserdel’ordre de D inode N,queéselqueesperàvem.

Unatercerapossibilitatésminimitzarunanormadiferentdel’euclidiana: perexemple,lanorma L1.Aquestanorma,enuncertsentit,estàmésben adaptadaalararesadelsvectors.Genèricament,elvectord’unavarietatlineal queminimitzalanorma L1 tendeixaserrar,comesveualafigura1.

norma L2

norma L∞

norma L1

Figura 1: Elsgràficsmostrenlaselecció,enunavarietatlineal(enaquest casunarecta),delvectorqueminimitzaunacertanorma.Equivalentment,mostrencomunabolaassociadaalanormavacreixentfinsque tocaalavarietatlineal.Observi’squetansolsperalanorma L1 elpunt decontacteésunvectorrar(enelseixosdecoordenades).

JoaquimBruna

Enconseqüència,semblaraonableferlarecuperaciódelsvectorsrarsminimitzantlanorma L1.Tornantalnostreproblema,definim ∆(Y) comelvector Z ∈ B(Y) queminimitzi Z 1.Ésadir,perrecuperar X,estudiem ˆ X = ∆AX = Z talque AZ = AX minimitzi Z 1.Entretotselsvectorsquesóncoherentsamb lesobservacions,prenemelqueminimitzalanorma L1

Aquestésunproblemadeprogramaciólinealqueespottractarcomputacionalmentd’unaformamolteficient.

Elteoremasegüentconfirmalesexpectatives.

Teorema 3. Suposemquelamatriu A compleixlapropietatRIPd’ordre 2N amb δ2N < √2 1.Aleshores,lasolució ˆ X definidaanteriormentcompleix

• ˆ X X ≤ C X XN 1 √N

• ˆ X X 1 ≤ C X XN 1.

Amés,aquestareconstruccióésrobusta:sidonat ε> 0 posem B(Y) ={Z ∈ RD amb AZ Y ≤ ε},lasolució ˆ X compleix

ˆ X X ≤ C X XN 1 √N + Cε.

Aquestteorema,demostrata[5],ésunresultatbastantnotable.Endestaquemelspuntssegüents:

1. Si X és N-rar,aleshores X = XN itenimreconstruccióexacta.Sino,ens diuquelaqualitatde ˆ X,mesuradaperl’error ˆ X X 1,éstanbonacom siconeguéssimd’antuviles N coordenadesmésgransde X.I,amés,és robust.

2. L’algorisme ∆ ésindependentde N,delesposicionsdelscoeficientside lessevesmagnituds.Silamatriu A télapropietatRIPd’ordre2N,tindrem reconstruccióexacta.

6Icomtrobemmatrius M × D demostratge A quetinguinla propietatRIPd’ordre N?

Elteoremaanteriorésprousatisfactorisemprequesiguemcapaçosdetrobar matriusdemostratgequecompleixinlahipòtesi.Defet,ensinteressatambé quehocompleixinamb M —elnombredemostres—elméspetitpossible, idealmentdel’ordrede N.Opodempensar-hoalrevés:amb M fixat,ens interessaque N siguielmésgranpossible.Hihaconstruccionsdeterministes dematrius A quecompleixenlahipòtesi,peròamb M massagran.Comsovint passa,però,lesconstruccionsaleatòriesgairebésemprefuncionen.

Perexemple,hompotprovarquesiesprenenlesentradesde A independentsiidènticamentdistribuïdessegonsunalleicontínua,escomplirà s(A) = m + 1ambprobabilitat1.Elresultatqueensinteressaés,però,el següent:

Teorema 4 Consideremlesmatriusaleatòriesdemida M × D obtingudesd’algunadelesmaneressegüents:

1. Triant D vectorscolumnaal’atzar(ambdistribucióuniforme)al’esfera unitatde RM .

2.Prenentcomaentradesde A variables N(0, 1 M ) independents.

3. Prenentcomaentradesde A variablesindependentsambvalors ± 1 √M de probabilitat 1 2 .

Llavors,si M ≥ CN log D N , A compleixlapropietatRIPd’ordre 2N ambconstant < √2 1,ambunaprobabilitat ≥ 1 e cM ,on c ésunaconstantquedepèn de C.

Aquestresultatnoésdifícildeprovar:ésconseqüènciadelsanomenats fenòmensdeconcentraciódemesura;vegeu[1].Elqueéssignificatiuenel resultatéselfetque M ≥ CN log D N ,ésadir,que M noéspasgairemésgran que N.Aquestacotainferiorde M ésòptimaenelteorema,perquèhompot provarquetotamatriu M × D quecompleixilapropietatRIPd’ordre2N amb constant δ< 1 2 hadesatisferl’acotacióinferioranteriorpera M

Endefinitiva,hemvistqueunaestratègiaefectivaésagafarmatriusde mostratgealeatòriesiutilitzarlaminimitzacióennorma L1

Elcasgaussiàtéunvalorafegitrellevant.Tornemalcomençament,quan lamatriudemostratgeera A = ΦΨ .Teníem f = Ψ X,ifemunmostratgede f amb Φ, Y = Φf , Y = y1,y2,...,yM ).Considerem f ∗ = Ψ X∗,on X∗ éselvector denorma L1 mínimatalque

Ψ X∗,φk = yk,k = 1,...,M.

Si f ésrarenlabase Ψ i A compleixleshipòtesisdelteorema3,tindremreconstruccióexacta, f ∗ = f .Arabé,si Φ ésgaussianaenelsentitdelteorema4, A tambéésgaussianaperatota Ψ iserviràcomamatriualeatòria.

Aixòsignificaquel’algorismefuncionaràperatoteslesbases Ψ , Φ,ésadir, ésuniversal.Ditd’unaaltramanera,nonecessitemsaberenquinabase f és rara,nomésquehoésenalguna!

7Lacoherènciaentreduesbasesortonormals

Hihaaltresmaneresd’aproximar-sealconceptede bonamatriudemostratge. Unad’ellesestàbasadaenlanocióde coherència entreduesbases.Suposarem quelesfuncions φk amblesqueprenemmostresformenpartd’unabase ortonormal.Ditd’unaaltraforma,lamatriu Φ,demida M × D,ésunamatriu obtingudatriant M filesd’unamatriuortonormal Γ

Definició 5 Lacoherènciaentreduesmatrius(bases)ortonormals Ψ , Γ d’ordre D × D és

µ(Ψ , Γ ) = √D max i,j γi,ψj , on Γ = (γ1,...,γD), Ψ = (ψ1,...,ψD).

Estracta,doncs,d’unamesuradelgraudecorrelacióexistententreambdues bases,que,perdefinició,ésunnombreentre1i √D.Elcoeficientdenormalització √D estàposatenrelacióambl’exemplesegüent,queésl’exemple principald’unparelldebasesincoherents.Prenemcoma Ψ labasedeFourier,

ψj (k) = D 1 2 ei2πjk/D,icoma Γ labasecanònica γj (k) = δ(j k).Òbviament, µ(Ψ , Γ ) = 1itenimmàximaincoherència.

Elteoremasegüentésdelmateixesperitqueelteorema3quanl’apliquem aunamatriualeatòria.Aquí, A éslamatriualeatòria ΦΨ ,on Φ consisteixa prendre M columnesal’atzarde Γ . Teorema 6 ([3]). Suposemque f és N-rarenlabase Ψ .Triem M mesuresa l’atzarentrelescorrelacionsde f respectedelabase Γ , f,γi .Si

M ≥ µ2(Ψ , Γ )N log D, llavorslasoluciódelproblema f ∗ = Ψ X∗,on X∗ éselvectordenorma L1 mínimatalque

yi = γi, Ψ X∗ , ésexactaambprobabilitatmoltproperaa 1.

Elteoremaensdiuque,peraconseguirminimitzarelnombredemostresi aconseguirreconstruccióexactaambprobabilitat1,commésincoherentssiguin lesbases,millor.Enelcasdel’exempledeFourierdemàximaincoherència, quèensdiuaquestteorema?Ensdiuquesiunsenyaldemida D és N-raren freqüència, f(t) = D 1 j=0 xj e2πijt/D,X ∈ ΣN (6)

llavorséspossiblereconstruir f apartirdelsseusvalorsen M = N log D enters presosal’atzarentre1i D,igairebétoteslestriesvanbé.Insistimuncopmés queaixòfuncionasensecapconeixementprevidequinessónles N-freqüències activesnilessevesamplituds.Dualment,si f és N-rara RD,espotrecuperar f apartirde N log D coeficientsdeFourierpresosal’atzar,igairebétotesles triesvanbé.Aquestresultat,demostrata[4],vaprecedirelteoremagenerali fouundelsprimersenlateoria.Ésinteressantcontrastar-loambelteorema deterministasegüent:si f éscoma (6),éspossiblereconstruir f exactament apartirdelsseusvalorsen1, 2,..., 2N o,mésgeneralment,en2N enters consecutiusqualssevol.Aquí, N log D éssubstituïtperlamillorcota2N,però ladiferènciaestàenelfetque,enelresultatqueacabemd’esmentar,gairebé toteslestriesde M = N log D entersfuncionen.Tambéésrellevantelfetque, sihomvolquegairebétotesles M triesd’entersvaginbé,llavorscalque M ≥ N log D,ésadir,elresultatésòptim.

D’altrabanda,nopothaver-hiunteoremad’aquestestilsenselacomponent aleatòria,ésadir,deformaquelareconstrucciósiguipossiblepera totes les triesde M enters.Aixòésperquèhihasenyals f , N-rarsdemida D,quetenen D N coeficientsdeFouriertotsnuls.

Altresexemplesdebasesaltamentincoherentss’obtenenprenentcoma Ψ lesbasesd’ondetesdeDaubechiesicoma Φ lesanomenades basesdenoiselets; vegeu[9].

Referències

[1] Baraniuk,R.;Davenport,M.;DeVore,R.;Wakin,M. «Asimpleproofof therestrictedisometrypropertyforrandommatrices». Constr.Approx., 28(3)(2008),253–263.

[2] Candès,E.J. «Therestrictedisometrypropertyanditsimplicationsfor compressedsensing». C.R.Math.Acad.Sci.Paris,346(9–10)(2008), 589–592.

[3] Candès,E.;Romberg,J. «Sparsityandincoherenceincompressivesampling». InverseProblems,23(3)(2007),969–985.

[4] Candès,E.J.;Romberg,J.;Tao,T. «Robustuncertaintyprinciples:exact signalreconstructionfromhighlyincompletefrequencyinformation». IEEE Trans.Inform.Theory,52(2)(2006),489–509.

[5] Candès,E.J.;Romberg,J.K.;Tao,T. «Stablesignalrecoveryfromincompleteandinaccuratemeasurements». Comm.PureAppl.Math.,59(8) (2006),1207–1223.

[6] Candès,E.J.;Tao,T. «Decodingbylinearprogramming». IEEETrans. Inform.Theory,51(12)(2005),4203–4215.

[7] Candès,E.J.;Wakin,M.B. «Anintroductiontocompressivesampling». SignalProcessingMagazine,IEEE,25(2)(2008),21–30.

[8] Cohen,A.;Dahmen,W.;DeVore,R. «Compressedsensingandbest k-term approximation». J.Amer.Math.Soc.,22(1)(2009),211–231.

[9] Coifman,R.;Geshwind,F.;Meyer,Y. «Noiselets». Appl.Comput.Harmon. Anal.,10(1)(2001),27–44.

[10] Eldar,Y.C.;Kutyniok,G. (ed.). Compressedsensing.Theoryandapplications.Cambridge:CambridgeUniversityPress,2012.

DepartamentdeMatemàtiques

UniversitatAutònomadeBarcelona bruna@mat.uab.cat

ButlletídelaSocietatCatalanadeMatemàtiques Vol.30,núm.2,2015.Pàg.125–166. DOI:10.2436/20.2002.01.61

Modelsestocàsticsmultiescala deladinàmicadepoblacionscel.lulars: mètodesasimptòticsinumèrics

PilarGuerreroiTomásAlarcón

Resum: Enaquestarticle,presentemunanovametodologiaquepermetformular ianalitzarmodelsestocàsticsmultiescaladeladinàmicadepoblacionscel.lulars. Seguintlaideademodelshíbridsmultiescalaexistents,creemelnostremodelde formajeràrquicad’acordamblesescalestemporalscaracterístiquesinvolucrades,on ladinàmicaestocàsticadelapoblacióestàgovernadaperlestaxesdenaixementide mortalitatsegonselqueprescriuenlescorresponentsviesintracel lulars(perexemple, elmodelestocàsticdelciclecel lular).Elmecanismederetroalimentacióestancaamb l’acoblamententreladinàmicadelapoblacióiladinàmicaintracel.lularatravésdela concentraciód’oxigen:lescèl.lulesconsumeixenoxigen,elqual,alseutorn,regulala taxaamblaquallescèl.lulesevolucionenalllargdelseuciclecel.lular.L’acoblament entreladinàmicaintracel.lularilapoblacionalesduuatermeatravésd’unmètode innovador,quepermetobtenirlataxadenaixementapartirdelmodelestocàsticdel ciclecel lular,basatenunenfocamentdetempsmitjàdeprimerpas.Sesuposaquela proliferaciócel lularésactivadaquanunaomésdelesproteïnesinvolucradesenlavia deregulaciódelciclecel lulararribaaunvalorllindar.Aquestpuntdevistapermet calcularlataxadedivisiócomafunciódel’edatdelacèl lulail’oxigenextracel lularen termesdeltempscorresponentdeprimerpas.Aleshores,podemprocediraformular ladinàmicaestocàsticadelespoblacionscel.lularsentermesd’unaequaciómestra estructuradaperl’edat.Amésamés,tambéhemdesenvolupatgeneralitzacionsde mètodesasimptòticsdeltipusWKBperal’equaciómestraestructuradaperl’edat,així comunmètodedesalt τ persimularl’evoluciódelapoblacióestructuradaperl’edat. Finalment,il lustremaquestametodologiageneralambunexempled’unapoblació cel lular,onlaprogressióenelciclecel lularestàreguladaperladisponibilitatd’oxigen.

Paraulesclau: modelitzaciómultiescala,modelitzacióestocàstica,càncer,ciclecellular.

ClassificacióMSC2010: 92B05.

Aquesttreballvaaparèixerenanglèsambeltítol«Stochasticmultiscalemodelsofcellpopulation dynamics:asymptoticandnumericalmethods»a Math.Model.Nat.Phenom.,vol.10,n.1(2015), 64–93.Agraïmalseditorsd’aquestarevistaelpermísperpublicar-nelatraducció,degudaa NúriaFolguera.

1Introducció

Enelsdarrersanys,lamodelitzaciómultiescaladesistemesbiològicshaesdevingutuncampderecercamoltactiu,ihafetcontribucionssignificatives endiversesàrees,quevandesdelacardiologia[25, 31, 36, 51]finsala biologiadeldesenvolupament[26, 40, 49, 50, 62]ielcreixementtumoral [2,11,14,15,27,33,34,41,42,43,44,45,47,48,55,56,57].

L’interèsquemoul’incrementd’esforçdedicataldesenvolupamentdemodelsitècniquesmultiescalaestàmotivatperlaconstatacióqueelmètodedela balamàgica [54]peraltractamentdemalaltiescomplexes,i,mésprecisament, enelcasdelcàncer,potserquenosiguitanefectiucominicialments’havia pensat.Pelquefaaltractamentdelcàncer,aquestconceptevaserpresentatper PaulEhrlich[54]iconsisteixenunateràpiadirigidaqueactuaespecíficament encèl.lulescancerígenes,iquedeixasensedanyarlescèl.lulesnormals.Amb l’arribadadelarecercagenòmica,s’esperavaqueaquestmètodefosimpulsat considerablement.Defet,durantmésdetrentaanys,larecercaenoncologia haestatdominadaperunaaproximaciógenocèntrica,onlesteràpiesdirigides, ésadir,medicamentsdesenvolupatsambl’objectiud’interferirambproductes específicsdegenscancerígens,hanestatelcentreil’objectiufonamentaldela biologiadelcàncer[39].Elsavençosengenòmicaialtres òmiques (proteòmica, epigenòmica,etc.)hanpromogutencaramésaquestenfocament.Noobstant això,l’èxitd’aquestaaproximacióentermesdedesenvolupamentdenous medicamentseficientsperalcàncers’haquedatllunydelesexpectatives[39].

Hihadiversesraonsperlesqualselmètodedela balamàgica hatingutun èxitlimitat.Elcomportamentilescaracterístiquesglobalsdelescèl.lulesen respostaalsestímuls,ésadir,elfenotip,emergeixenapartird’unacomplexa xarxad’interaccionsentreelsgensielsseusproductes,laqual,finalment, acabaregulantl’expressiódelsgens(vegeu,perexemple,eltreballrecentde Lignet etal. pelquefaalaxarxadesenyalitzacióVEGF[32]).Aquestesxarxes deregulaciódelsgensconstitueixenunadinàmicanolineal,dedimensiómolt gran,l’estructuradelesqualshaanatprenentformaperl’evoluciódegudaa laselecciónaturali,pertant,posseeixenpropietatscomararobustesa(ésa dir,resistènciadelfenotipencontrad’alteracionsgenètiques)icanalització (ésadir,l’habilitatdelsfenotipsd’incrementarlasevarobustesaamesura queeltempsavança).Aquestespropietatssónexplotadespelstumorspertal d’incrementarelseupotencialdeproliferacióiperresistiralesteràpies[29].A partdelescomplexesinteraccionsnolinealsentrecèl.lules,existeixenintricadesinteraccionsentrediferentscomponentsdelssistemesbiològicsatotsels nivells:desdecomplexesviesdesenyalitzacióixarxesderegulaciógèniques finsacomplexosefectesnolocals,onlespertorbacionsatotelteixitindueixen canvisanivelldelscaminsintracel.lularsdelescèl.lules[2, 14, 34, 41, 44, 48].

Aquestsialtresfactorsportencapaunacomplicadadinàmicaenteixitsbiològics.Enparticular,acausadetoteslescapesdecomplexitatquehiintervenen, ésmoltdifícild’avaluarelprincipaldogmadelmètodedela balamàgica,ésa dir,sabersiunagentterapèuticseràefectiuencontradeltumoriinofensiu peralteixitsaquehihaalvoltant.

Modelsestocàsticsmultiescaladepoblacionscel.lulars 127

Pertald’abordarirespondreaaquestesqüestions,s’haintensificatlarecerca eneldesenvolupamentil’anàlisidemodelsmultiescala.Aquestsmodelssón capaçosd’incorporarenunsolmodeldiferentssubmodelscorresponentsa diversosnivellsd’organitzacióbiològica(intracel.lular,interaccióentrecèllules,nivelldelteixitcomplet,etc.),elsquals,normalment,estancaracteritzats perdiferentsescalestemporalsidelongitud,aixícoml’acoblamententre aquestssubmodels,deformaqueelcomportamentglobaldetotelteixitpot seranalitzatcomunapropietatemergentdelselementsacoblats[11, 14, 33, 41,47,56].

Elsmodelsmultiescalapodenserformulatsdediversesmaneres.Una d’aquestesmetodologiesésl’anomenada modelitzacióhíbrida [2, 28, 34, 41, 47, 48].Elsmodelsmultiescalahíbridsestanformatsperdiferentssubmodelsper adiferentsnivellsd’organitzacióbiològica(processosintracel lulars,interacció entrecèl.lules,secrecióitransportdesenyals,etc.),icadaunésmodelat entermesdedescripcionsmatemàtiquesdiferents(equacionsdiferencials ordinàries,EDO;autòmatscel lulars;equacionsenderivadesparcials,EDP;etc.).

Elsmodelshíbridsestancaracteritzatsnormalmentperl’úsdemodelsbasatsen elsindividusperdescriureladinàmicade,comamínim,undelscompartiments cel.lularsconsideratsalmodel[42, 43].Altresfases(perexemple,poblacions cel lularsnomodeladescomaindividusifasesfluïdescomlasangoelfluid intersticial)sónmodeladesmitjançantEDPcomafasescontínues[28, 34].Els modelsbasatsenelsindividussóncomplementatsnormalmentambmodelsper alcomportamentdecèl lulesenrespostaasenyalscomlamancadenutrientso amolèculesdesenyalització[2].Laconcentraciódenutrientsodemolèculesde senyalitzacióésmodeladanormalmentcomuncampcontinumitjançantEDP deltipusreacció-difusió.Elsmodelshíbridshanestatproposatsperestudiar diferentsaspectesdelcreixementtumoral,comaralarespostaalateràpia [2,48],l’angiogènesiinduïdapeltumor[34,42,43]iladinàmicaevolutivadel creixementtumoral[47].

Unaaltraformapossibled’estudiarlamodelitzaciómultiescalaésusantels modelsdefasesmúltiples[10, 33, 45, 57].Enaquestsmodels,cadatipuscellularésmodelatcomunafasediferent.Elsmodelsdefluidsdefasesmúltiples hanestatutilitzatsperanalitzaraspectesdiferentsdelcreixementtumoral,on cadatipusdecèl.lulacorresponaunfluiddiferent[10, 33, 45].Elsmodelsde campdefases’hanutilitzatrecentmentpermodelarl’angiogènesiinduïdaper untumor[57].

Malgratelconsiderableesforçfetenelcampdelsmodelsmultiescalaper alcreixementtumoral,hihaaspectesdiversosdeladinàmicadelsteixits biològicsque,enaquestcontextdemodelització,encarasónpocconeguts.Un d’ellsésl’efectedelsoroll.Elsefectesaleatorishanestatinclososendiversos modelsmultiescalaobéhíbrids.Perexemple,elsmodelsd’angiogènesiinduïda tumoralmentdeMcDougall etal. [37, 38, 53],basatsenunestudiprevisobreun modelhíbridcontinu-discretd’AndersoniChaplain[5],oelsmodelsmultiescala peral’angiogènesiformulatsa[42, 43]tenenunelementestocàsticque,en aquestcas,corresponaconsiderarquelaformaciódevasosésrepresentadaen

termesd’unmodelesbiaixatdepasseigaleatoriperalmovimentdelescèl lules endotelialsmésexternes.Malgrattot,unametodologiageneralqueenspermeti incorporarianalitzarespecíficamentelsefectesdelsorolladiferentsescales encaranoexisteix.Comaprimerpasperompliraquestforat,proposemen aquesttreballunametodologiaperformularmodelsestocàsticsmultiescala deladinàmicadelespoblacionscel lulars,aixícomeldesenvolupamentde mètodesnumèricsiasimptòticsperalasevaanàlisi.

Enaquestarticle,ensproposemformularmodelsestocàsticsmultiescalade ladinàmicadepoblacionscel.lulars,elsqualstinguinenconsideraciófluctuacionsadosnivells:tantanivelldeviesdesenyalitzacióintracel lulars,acausa delbaixnombredeproteïnes,comanivelldepoblaciócel.lular,comaconseqüènciadetenirunapoblaciódemidafinita.D’araendavant,ensreferirema aquestesduesfontsdesorollcoma sorollmolecular i sorollcellular,respectivament.L’objectiud’aquestapublicacióésabordarelproblemadelsorollen sistemesmultiescalad’unaformasistemàtica.Ambaquestafinalitat,creem uncontextdetreballqueenspermetformularianalitzarmodelsestocàstics multiescala.

Pelquefaalacreaciódelnostremodel,faremlamateixasuposicióbàsica queesvafera[2],ésadir,dividiremelproblemaenlestrescapesqueconsiderem,queidentifiquemambprocessoscaracteritzatsperescalestemporals extensamentdiverses(vegeulafigura1peraunarepresentacióesquemàticadel nostremodelilesescalestemporalscaracterístiquesinvolucrades).Considerem unmodelonacoblemladinàmicadelaconcentraciódenutrientdisponible(per exemple,oxigen),determinadaperlasevataxadesubministramenticonsum perpartdelescèl.lules;unacapaintracel.lular,onconsideremunmodelque descriulamaneracomlaconcentraciód’oxigenregulalataxadeprogressió alllargdelciclecel lular[1, 7]i,pertant,tambélataxadedivisió,i,finalment, unacapacel.lular,onconsideremladinàmicaestocàsticadelespoblacions decèl lules.Lescapesintracel lularicel lularestanacobladesmitjançantun modelperalataxadedivisióquedepèndel’oxigen,formulatentermesd’un problemadetempsmitjàdeprimerpas.

L’articleestàorganitzatcoms’explicatotseguit.Alasecció2,descrivimla formulaciódelmodel.Hidiscutimelmodelestocàsticperalaprogressiódel ciclecel lularregulatperl’oxigen,iplantegemlaformulaciód’unmodelperala taxadedivisióquedepèndel’oxigenil’edatcomunproblemadetempsmitjà deprimerpasassociataladinàmicaestocàsticadelciclecel lular.Després procedimaformularunprocésestocàsticdenaixement-mortquedepènde l’edatperaladinàmicadelespoblacionscel lulars.Alasecció3,presentem unmètodeasimptòticWKB(Wentzel-Kramers-Brillouin)pertrobarsolucions aproximadesperal’equaciómestra(EM)corresponentquedepèndel’edat. Lasecció4estàdedicadaalaformulaciód’unmètodedesalt τ quedepèn del’edatqueenspermetfersimulacionsdelmodelestocàsticmultiescala. Finalment,alasecció5,s’hidiscuteixenelsnostresresultats,leslimitacions d’aquestenfocamentilesdireccionsperaunarecercafutura.

Figura 1: Representacióesquemàticadelmodelmultiescala:l’oxigen modulalaprogressiódelescèl.lulesalllargdelciclecel.lularo,equivalentment,lasevataxadedivisió.Lataxadedivisióquedepènde l’oxigenésmodeladaentermesd’unproblemadetempsmitjàdeprimer pasi,després,ésusadaal’equaciómestraquedeterminaladinàmica estocàsticadelapoblaciócel.lular.Lescèl.lulesconsumeixenoxigeni, enconseqüència,lasevadinàmicaregulalaconcentraciód’oxigen,de maneraquetancaelmecanismederetroalimentació.Tambémostrem lesescalestemporalscaracterístiquescorresponents:desenesdemillisegonsperal’oxigen,minutsohoresperalsprocessosintracel lularsi diesperalescèl.lules.

2Formulaciódelmodel

2.1Estructurageneraldelmodelestocàsticmultiescala

Abansdepassaraferunadiscussiódetalladadelsdiferentselementsinvolucratsenlaformulaciódelmodelestocàsticmultiescala,procedimauna descripciódetalladadel’estructurageneraldelmodel,laqualestàaltament relacionadaambladelmodelproposata[2].

Elmodelquepresentemenaquestarticleintegrafenòmenscaracteritzats perescalestemporalsdiferents,comespotveureesquemàticamentalafigura1, ons’inclouenellliuramentdel’oxigenalapoblaciócel lularielconsumd’aquest perpartdelescèl.lules,ladinàmicadelapoblaciócel.lularsotalarestricció d’unsubministramentd’oxigenaunataxafinitailaproliferacióil’apoptosi deladivisiócel.lular.Lasevaestructuraés,pertant,forçacomplexai,per aquestaraó,abansdepresentarelssubmodelsinvolucratsenladescripcióde cadaund’aquestsprocessos,explicareml’estructuraglobaldelcontextdela modelització.

Elpuntdevistaquenosaltresutilitzemésunageneralitzaciónaturaldel procésdeMarkovestàndarddenaixement-mortatempscontinuilaseva descripcióviaunaequaciómestra[17].Comveurem,elcaràctermultiescala delsistema,ésadir,lainclusiódel’estructurafisiològicaassociadaales variablesdelciclecel.lular,introdueixunaestructurad’edatalapoblació:la taxadedivisiódepèndel’edatdelacèl lula(i.e.,eltempsquehatranscorregut desdel’últimadivisió),quedetermina,atravésdelmodeldeciclecel.lular corresponent,l’estatusdinsdelciclecel lulardelescèl lulesrespectives.

Pelquefaalesparticularitatsdecadasubmodelinvolucrat,elmodelper allliuramentd’oxigenésunaequaciódiferencialestocàstica,onl’oxigenés proporcionataunataxaconstant F iconsumitperpartdelescèl lules(vegeu lafigura1).Elcaràcterestocàsticdel’equacióquegovernal’evoluciódela concentraciód’oxigensorgeixdelfetqueelnombredecèl lulesauntemps determinatésunavariableestocàstica.

Elsegonsubmodel(ésadir,elmodelintracel.lular)consideratenelnostre contextmultiescalaésunmodelestocàsticperalaprogressióatravésdelcicle cel.lularreguladaperl’oxigen(vegeulafigura1).Aquestsubmodelésformulat usantlestècniquesestàndarddemodelitzaciódecinèticaquímica[20],de formaqueellímitdecampmitjàdelmodelestocàsticcorresponalmodel deterministaperalciclecel.lularformulata[1].Aquestmodelproporciona l’estatusdelciclecel lular,ésadir,elnombredemolèculesdecadaproteïna involucradesenelmodel,d’onnosaltrespodemdeduirsilatransició G1/S hatingutllocperaunacèl lulad’unadeterminadaedat a.L’estatusdelcicle cel.lulard’unacèl.lulad’edat a estàdeterminatentermesdesil’abundànciade certesproteïnesqueactivenelciclecel.lular(ciclines)haarribatauncertvalor llindar.Enelnostrecasconcret,siaunaedat a elsnivellsdeciclinesestanper sotadelvalorllindarcorresponent,lacèl.lulaencaraestàa G1.Si,encanvi,el valorllindarjas’haassolit,aleshoreslacèl lulahapassata S i,pertant,està preparadaperdividir-se.Aixòimplicaquelaprobabilitatqueunacèl.lulahagi creuatelnivellllindardeciclinesaunaedat a potserformuladaentermes d’unproblemadetempsmitjàdeprimerpas(MFTP),enelqualhomanalitzala probabilitatd’unprocésMarkovd’arribaraunacertafrontera[17].Lataxaala qualelnostremodelperalciclecel lulararribaalvalorllindard’activaciódela ciclina,ditd’unaaltraforma,lataxaalaquallescèl.lulespassenatravésdel puntderestricciódelciclecel lular,esprendeformaquesiguiproporcional alataxadedivisió.Lataxadedivisióésfunciódel’edatdelacèl.lula,així comdelaconcentraciód’oxigen,jaquel’abundànciad’oxigenregulalataxade progressióalllargdelciclecel.lular.

Elterceriúltimsubmodel(ésadir,elmodelcel.lular)corresponaladinàmicadelespoblacionscel lularsiestàgovernatperl’equaciómestraperalafunció dedensitatdeprobabilitatdelnombredecèl.lules[17].Elprocésestocàsticque descriuladinàmicadelespoblacionscel.lularsésunprocésnaixement-mort quedepèndel’edat,onlataxadenaixementdepèndel’edatiésdeterminada pelmodelintracel.lular.Lataxademortés,persimplicitat,consideradaconstant.Comaconseqüènciadelfetquelataxadenaixementdepenguidel’edat,

Modelsestocàsticsmultiescaladepoblacionscel.lulars 131

lanostraequaciómestramultiescalanotélaformaestàndardperapoblacions noestructurades.És,encanvi,unaequaciómestraquedepèndel’edat.

Ladescripciódetalladadelsprocessosinvolucratsencadaundelssubmodelsquehanestatresumitsenleslíniesanteriorsésl’objected’estudidela partrestantdelasecció2.

2.2Escalaintracel.lular:modelestocàsticperalaprogressiódelcicle cel.lularquedepèndel’oxigen

2.2.1Informacióprèviasobrelamodelitzaciódelciclecel.lular. Elcicle cel.lularéslaseqüènciad’esdevenimentsmitjançantelsqualsunacèl.lulaque estàcreixentduplicatotselsseuscomponentsiesdivideixenduescèl.lules filles,cadaunadelesquals,alseutorn,télamaquinàriailainformaciósuficientsperpoderrepetirelprocés[4].Elciclecel lularestàdividit,normalment, enquatrefases: G1, S, G2 ilamitosi M.Durantlafase G1 (G = fasebuida),la cèl lulanoesdivideixielscromosomesnoesrepliquen.Lareplicaciódel’ADN nuclearocorredurantlafase S,mentrequelamitosiescompletaalfinalde lafase M.L’intervalentrelareplicaciódel’ADNiladivisiós’anomena fase G2 Lesfasesbuides G1 i G2 donenalacèl lulatempsaddicionalpercréixer.La cèl.lulatambépassaperduestransicionsirreversibles.Laprimerad’aquestes transicionsocorrealfinalde G1 is’anomena Inici.Durantlafase G1,lacèl lula controlaelseuentornilasevamida.Quanlescondicionsexternesilamidade lacèl lulasónlesadients,lacèl lulaesdedicaasintetitzarADNialasevadivisió. Aquestatransicióésirreversible:uncoplacèl.lulaentraalafase S ilareplicació del’ADNcomença,ladivisiós’had’acabar.Lasegonatransició, Acabament, ocorrequanlareplicaciódel’ADNjas’hacompletat.Uncoplacèl lulaha comprovatquel’alineaciódel’ADNilescromàtideshaocorregut,latransició Acabament ésactivadailacèl lula,finalment,esdivideixenduescèl lulesfilles. Uncinquèestat,l’anomenat estat G0,ésdefinitperreferir-sealescèl.lules quehanabandonatlaprogressiónormaldelciclecel lularihanesdevingut quiescents.Enaquestestat,lamajoria(totiquenototes)delesfuncions cel.lularsestansuspeses,d’entrelesqualslamésnotableéslaproliferació.

Elsesdevenimentsdelciclecel lularsóncontrolatsperunaxarxadesenyals molecularsquetenenpercomponentscentralslesproteïnes-cinasesquedepenendeciclines(CDK).Al’estat G1,l’activitatdelesCDKésbaixa,jaqueles sevesparellesobligades,lesciclines,nohisón.Aixòesdeualfetquelasíntesi perpartdel’ARNmdelesciclinesésinhibidailaproteïnaciclinaesdegrada ràpidament.Al’Inici,s’indueixlasíntesideciclinesis’inhibeixladegradació deciclines,laqualcosacausaunincrementincreïbleenl’activitatdelesCDK, queesmantédurant S, G2 i M.L’activitataltadelesCDKésnecessàriapera lareplicaciódel’ADN,lacondensaciódelscromosomesilaformaciódelfus. Al’Acabament,ungrupdeproteïnesqueformaranelcomplexpromotorde l’anafase(APC)ésactivat[63].L’APCenganxauna«etiquetadeconstrucció» aunesproteïnesdianaespecífiques,queacontinuaciósóndegradadesperla maquinàriadeproteòlisidelacèl lula.L’APCestàformatperunnuclicomplex

constituïtperunadotzenadepolipèptidsaproximadamentiduesproteïnes auxiliars,Cdc20iCdh1,quesemblaquetenenelpaper(quanestanactives) dereconèixerunesproteïnesdianaespecífiquesipresentar-lesalcomplexdel nucliperquèlesetiquetin[61, 63].L’activaciódelaCdc20al’Acabament és necessàriaperaladegradaciódecohesinesal’anafaseiperal’activacióde laCdh1.Deformaconjunta,Cdc20iCdh1etiquetenciclinesperdegradar alatelofase,laqualcosapermetalsistemadecontrolretornara G1.Calque distingimaquestesduesproteïnesauxiliars,jaquelaCdc20ilaCdh1són controladesdeformadiferentperlaciclina-CDK,laqualactivalaCdc20i inhibeixlaCdh1.

A[58],TysoniNovakdescriuenunmodelperalestransicionsirreversibles Inici i Acabament,lesqualsregulenlaprogressiódelciclecel.lular.Elmodelque presentemsuposaqueaquestestransicionsocorrenpermitjàdebifurcacions delsistemaregulador,laqualcosaportaalacreacióidestrucciód’estats estacionarisestablesdelsistemareguladormoleculardelprocésdedivisió cel lular.

Ladinàmicadelciclecel.lularpotestarafectadapercondicionsambientals, enparticular,pelnivelld’oxigenextracel.lular:ésbensabutqueconcentracions d’oxigenbaixes(hipòxia)alterenlaprogressiódelciclededivisiócel lular[18] idelatransició G1/S,enparticular.Alareferència[1],sesuposavaquela respostad’aquestatransicióalahipòxiaeramediadaperlaproteïnap27,un elementdelaxarxaCDK,laproducciódelaqualaugmentasotacondicions d’hipòxia[16, 18],encaraqueestudisrecentsposenalgunsdubtessobreelrol delap27comamediadoradelsefectesd’hipòxiaenlaprogressiódelcicle cel.lular[9, 23].Enelnostremodel,suposemquelap27intervéenl’aturadade latransició G1/S induïdaperlahipòxia,demaneraqueinhibeixlaformació delcomplexciclina-CDKi,pertant,inhibeixlasíntesidel’ADN.

A[1]esproposaunamodificaciódelmodeldeTysoniNovak[58],enla qualesconsiderenelsefectesdelahipòxiaenelciclecel lularatravésdels nivellsdelaproteïnap27.Lap27inhibeixlaformaciódelcomplexciclina-CDK. Amés,elsnivellsdep27s’incrementenenpresènciad’hipòxia.Així,elconjunt d’equacionsdiferencialsordinàries(EDO)introduïta[1]permodelarl’efecte delahipòxiaalafasedetransició Inici éselsegüent:

Modelsestocàsticsmultiescaladepoblacionscel.lulars 133

on x i y sónlesconcentracionsdeCdh1/APCactivesilaconcentraciódels complexosciclina-CDK,respectivament; z éslaconcentraciódep27; O2,laconcentraciód’oxigen; u,unactivadorgenèric; η,lataxadecreixementdela cèl.lula; m,lamassadelacèl.lula,i m∗ éslamassad’unacèl.lulaadulta.Els ai (i = 1, 2, 3, 4), czi (i = 1, 2), bi (i = 3, 4)sóntaxesconstants,i J3 i J4 sónles constantsdeMichaelis-Menten.TysoniNovak[58]trienunaescalaperales sevesequacionstalquelaconcentraciótotaldeCdh1(activaiinactiva)està normalitzadaa1ilesconstantsdeMichaelis-Menten, J3 i J4,sóntalsque J3 1i J4 1.Totiqueenelmodelproposata[1]esconsideraquelaciclina involucradaenlatransició G1/S ésCycBisesuposaqueelseuinhibidorés APC/Cdh1,estudisrecentssuggereixenque,encanvi,unarepresentaciómés acuradadelasituacióportariaaconsiderarCycEielseuinhibidorSCF[59].

Defet,enelsmamífers,laciclinaDestàinvolucradaenlaregulaciódela dinàmicalentadelafase G1 (inhibidaperp27),mentrequelaciclinaEregula ladinàmicaràpida(vegeulareferència[52]peraunadescripciódetallada). Unadescripciómoltacuradadelaregulaciódelatransició G1/S encèl.lulesde mamífershauriadetenirencomptelapresènciad’aquestesduesciclines,en llocdeconsiderarelsseusefectes grossomodo enunsolcompost.

2.2.2Formulacióestocàstica. Araprocedimaformularunmodelestocàstic peralaprogressiódelciclecel.lularreguladaperl’oxigencomunprocésde Markoventermesd’unaequaciómestra.Elmodelresultantseràanalitzat utilitzantelmètodeasimptòticWKBperasistemesdemidagran[3, 30, 35]. Aquest(sub)modelexpressalataxadeproliferaciódelescèl.lulescomafunció del’oxigenextracel lular.Aquestainformacióseràusadadesprésal’escala cel.lulardelmodelpoblacionalcomaparàmetre,ésadir,utilitzaremlataxade divisióquedepèndel’oxigenidel’edatdinsdel’equaciómestraquedescriula dinàmicadelafasecel.lular.

Elmodelquenosaltresproposemaquíestàbasatenelsmateixosprincipis bàsics[58]queelqueesvaformulara[1].TysoniNovak[58]vanproposar unmodelperalatransició G1/S,enelquall’elementcentraldelmodelés lainhibiciómútuaentrelaformaactivadeCdh1/APC,uninhibidordela progressiódelciclecel.lular,iCycB-CDK,l’activitatdelqualésnecessàriaper talqueelciclecel.lularpuguisotmetre’salatransicióabansmencionada. Aquestainhibiciómútuadónallocaunsistemabiestableambdosestats estacionarisestables:elpuntfixanomenat G1,onl’activitatdeCdh1éspropera alseumàximil’activitatdeCycBésvirtualmentinexistent,ielpuntfix S-G2-M, onpassaelcontrari.Amésamés,TysoniNovak[58]suposenquelainhibició deCdh1perpartdeCycBestàmoduladaperlamidacel lular:lainhibicióés inicialmentpobra,quanlescèl.luless’hanacabatdedividiriencaranohan arribatalamidacríticanecessàriaperaentraralafase S,peròaugmentaa mesuraquelescèl lulescreixenis’apropenalamidacrítica.Matemàticament, aquestesregulacionssegonslamidacel.lularindueixenunabifurcaciósellanode,onelpuntfix G1 esdestrueixquanlamidacel lular(massa)arribaaun

valorcrític,laqualcosaforçaelsistemaaincrementarl’activitatdeCycBia entraralafase S.A[1]esvaproposarunamodificaciód’aquestmodelsimple, segonlaqualuninhibidoraddicionaldel’activitatdelesciclines,p27,vaser introduït.Sesapquel’activitatdep27augmentaquanfaltaoxigen(hipòxia),la qualcosaretardal’inicidelatransició G1/S.Aquestmodelenspermetacoblar lataxadeprogressiódelciclecel lularambl’abundànciad’oxigeni,pertant, analitzarelsefectesdelesfluctuacionsenl’aportaciód’oxigenenelcreixement tumoral[2].

Figura 2: Representacióesquemàticadelesreaccionsinvolucrades enelmodelestocàsticdelaprogressiódelciclecel.lularreguladaper l’oxigen. M éslamassadelacèl lula, X (X1)éselnombredemolèculesCdh1actives(inactives), E1 (E2)éselnombred’enzimsactivadorsde Cdh1(inactivadors), C1 (C2)éselnombredecomplexos X1E1 (XE2), Y és elnombredecomplexosciclina-CDKi Z éselnombredemolèculesp27. Lesreaccions(a)i(b)corresponenal’activacióiinactivaciócatalitzada perenzimsdeCdh1,respectivament.Esfanotarquelareacciód’inactivacióésincentivadaperCycB(Y )imoduladaperlamidacel.lular(M).

Lesreaccions(c)i(d)determinenladinàmicadelnombredemolècules activesCycBip27.CycBéssintetitzadaaunataxaconstantidegradadaa unataxaquedepèndelaCdh1activa,aixícomdelap27.p27éssintetitzadaaunataxaquedepèndelamidaidegradadaaunataxaquedepèn del’oxigen.D’acordamb[1], g(M) = 1 M/m∗ i f(O2) = O2/(B + O2). Lestaxesconstantsespodenveurealataula2.

Lesreaccionsinvolucradesenelnostremodelestocàsticdelaprogressió delciclecel.lularreguladaperl’oxigenespodenveureesquemàticamentala figura2: M denotalamassadelacèl lula; X (X1)éselnombredemolècules Cdh1actives(inactives); E1 (E2),elnombred’enzimsactivadors(inactivadors) deCdh1,i C1 (C2),elnombredecomplexos X1E1 (XE2).Amés, Y i Z es refereixenalnombredecomplexosciclina-CDKialnombredemolèculesp27, respectivament.

Lesreaccionsdelafigura2(a)i(b)corresponenalesreaccionscatalitzades perenzimsd’activacióiinactivaciódeCdh1,respectivament.Femnotarque, coma[58],lainactivaciódeCdh1ésincentivadaperCycBactiva(Y )iestà

Modelsestocàsticsmultiescaladepoblacionscel.lulars 135

moduladapelcreixementcel lular(M).Lareacciódelafigura2(c)explicala dinàmicadelnombredemolèculesactivesCycB, Y :CycBéssintetitzadaauna taxaconstantiésdegradadaaunataxaquedepèntantdel’activaCdh1(X)(la qualcosatanca,pertant,elmecanismederetroalimentaciónegatiud’inhibició mútuaentreCdh1iCycB)comdelnombredemolèculesp27(Z),laqualcosa implementaenelmodelelroldep27comainhibidordel’activitatdeles ciclines.Finalment,lareacciódelafigura2(d)determinaladinàmicadel nombredemolèculesp27, Z:p27éssintetitzadaaunataxaquedepèndela midacel.lularidegradadaaunataxaquedepèndel’oxigen,deformaque,quan l’oxigenésescàs,ladegradaciódep27esredueix.Aquestefecteportaauna acumulaciódep27queretardalaprogressiódelciclecel.lular,laqualcosa incrementalainhibiciódel’activitatdelesciclines.Ellectorpotconsultara[1] totselsdetallssobreelraonamentbiològicd’aquestmodel.

Elmodelestocàstics’especifica,pertant,entermesdelvectord’estat, → X(a):

→ X(a) = (M(a),Z(a),X1(a),E1(a),C1(a),X(a),E2(a),C2(a),Y(a)),

on a represental’edat,queesprencomeltempsquehapassatdesdela darreradivisiócel.lular.Ladinàmicadelmodelesdescriumitjançantladensitat deprobabilitatqueelsistemaestiguial’estat → X al’edat a, Ψ ( → X,a),ladinàmica delaqualestàdeterminadaperl’equaciómestra(EM):

∂Ψ ( → X,a) ∂a = i (Wi( → X ri,a)Ψ ( → X ri,a) Wi( → X,a)Ψ ( → X,a)), (2.1)

on Wi( → X,a) sónlestaxesdetransiciócorresponentsacadaunadelesreaccions elementalsinvolucradesenelmodelmostradesalafigura2,i ri ésunvector quetéperentradesl’incrementenelnombredemolèculesdecadaespècie molecularquanlareacció i ocorre,ésadir, P( → X(a + ∆a) = x(a) + ri | x(a)) = Wi( → X,a)∆a.

Lestaxesdetransiciócorresponentsalesreaccionsenzimàtiquesdela figura2espodenveurealataula1.Permodelarlacinèticadelesreaccions químiquesdelafigura2,hemutilitzatlalleid’acciódelamassa(LMA)[20], incloseslesreaccionsenzimàtiques,talcoms’indicaalafigura2(a)i(b). HemtriatlacinèticaLMApermodelaraquestesreaccionsenllocd’utilitzarlacinèticaMichaelis-Mentenperraonstècniques,queestanrelacionadesambl’anàlisiasimptòticadel’equació (2.1) quefemalasecciósegüent: elmètodeasimptòticWKBdemanaquelestaxesdetransició Wi satisfacincerteslleisd’escalament(vegeul’equació (2.3) mésendavant).Aquesta relaciód’escalamentnosesatisfàamblestaxesMichaelis-Menten,ihem, pertant,derecórreralacinèticaLMA.Noobstantaixò,aquestfettambé implicaquecalanarambmoltacautelaquanesparametritzielmodel,ja

queelsvalorsdelsparàmetresdonatsa[58],onesvautilitzarlacinèticaMichaelis-Mentenperamodelarl’activacióiinactivaciódeCdh1catalitzadaperenzims,nosóndirectamentaplicablesalnostremodel.Al’apèndixA,tractemaquestproblemaitrobemlarelacióentreelsparàmetresusats a[58]ielsnostres.

Probabilitatdelareaccióp.u.t. → r i

W1 = η m∗Ω M(M 1) 2 ( 1, 0, 0, 0, 0, 0, 0, 0, 0)

W2 = ηM(1, 0, 0, 0, 0, 0, 0, 0, 0)

W3 = cz1 Ω (0, 1, 0, 0, 0, 0, 0, 0, 0)

W4 = cz1 M m∗ + cz2 O2 B+O2 Z(0, 1, 0, 0, 0, 0, 0, 0, 0)

W5 = d1 Ω X1E1 (0, 0, 1, 1, 1, 0, 0, 0, 0)

W6 = d 1C1 (0, 0, 1, 1, 1, 0, 0, 0, 0)

W7 = d4 Ω2 YMC2

W8 = d2C1

W9 = d3 Ω3 XYME2

W10 = d 3 Ω2 YMC2

(0, 0, 1, 0, 0, 0, 1, 1, 0)

(0, 0, 0, 1, 1, 1, 0, 0, 0)

(0, 0, 0, 0, 0, 1, 1, 1, 0)

(0, 0, 0, 0, 0, 1, 1, 1, 0)

W11 = a4Ω (0, 0, 0, 0, 0, 0, 0, 0, 1)

W12 = a1 + a2 Ω X + a3 Ω Z Y(0, 0, 0, 0, 0, 0, 0, 0, 1)

Taula 1: Probabilitatdelareaccióperunitatdetemps, Wi ≡ W( → X, → r i,a), amb → r i = (rim,riz,rix1 ,rie1 ,ric1 ,rix ,rie2 ,ric2 ,riy ), i = 1,..., 12.

2.2.3Anàlisidelmodel:aproximacióWKB. Lametodologiaqueusemper analitzarelnostremodelestàbasadaenl’aproximacióWKBivaserproposada perprimeravegadaperKubo etal. [30],elsqualsprovenque,sotalahipòtesi adequadad’escalament,lasolucióquedepèndeltempsdel’EM,equació (2.1), potseraproximadaperunafunciódelmateixtipusqueladelasolucióal’equilibri,ésadir,l’exponenciald’unafuncióhomogèniade → X ,queanomenarem S, Ψ ( → X,a) = C exp( S( → X,a)) = C exp( Ωs(→ x,a)), (2.2) on Ω ésalgunamesuradelamidadelsistemai → x = → X/Ω;vegeu[6].També mostrenquelestaxesdetransició W( → X,r,a) handeserfuncionshomogènies de → X pertald’obtenirunasoluciódel’EMdeltipusdel’equació(2.2), Wi( → X,a) = Ωwi(→ x,a), → x = → X Ω . (2.3)

Enconseqüència,laprobabilitatquepassiunadeterminadareaccióenun intervaldetempsinfinitesimalésproporcionalalamidadelsistema, Ω,i

Modelsestocàsticsmultiescaladepoblacionscel.lulars 137

estàdeterminadanomésperl’estatdelsistema,representatpelconjuntdeles variablesintensives → x .Ladefinició

ψ(→ x,a) = ΩΨ ( → X,a),

juntamentambl’equació (2.3),enspermetescriurel’EM (2.1) enlaformaWKB: 1 Ω ∂ψ(→ x,a) ∂a = i (e ((ri/Ω)·(∂/∂x)) 1)wi(→ x,a)ψ(→ x,a),

onhemusatque e r ·(∂/∂x) éselgeneradordelestranslacionsenl’espaid’estats delsistema.

Percontinuar,consideremlafunciócaracterísticade ψ(→ x,a),

Q(u,a) = ∞ −∞

ψ(→ x,a)eiu → x d→ x, (2.4)

ilasevafunciógeneratriudecumulantsassociada, q(u,a) ≡ log(Q(u,a)) [3, 30].Elscumulants qn(a) de ψ(→ x,a) podenserobtingutsapartirdeldesenvolupament: q(u,a) = ∞ n=1 in n! un · qn(a),

on un representaelproducte n-àdicdefinitper (un)j1,j2,...,jn ≡ n i=1 uji iel puntvolatdenotalacontracciótotalsobretotselsíndexs n.Espotveurea[3] quedel’equació(2.4)esdedueix: 1 Ω ∂Q(u,t) ∂t = 1 (2π)d i e iu yi 1

wi(v,a)Q(u v,t)dv, (2.5)

on wi(v,a) éslatransformadadeFourierde wi(→ x,a) i d éselnombred’espèciesquímiquesenelnostremodeldeciclecel.lular.Kubo etal. a[30]mostren quel’equació (2.5) éselpuntd’iniciperaundesenvolupamentasimptòticdel tipusWKB,ons’obtéunajerarquiatancadad’equacionsdiferencialsordinàries peralscumulants(qn(a))delprocés.

Kubo etal. [30]provenque,pera n arbitrària,elscumulantsdeladistribució deprobabilitat(e.g., (q1)i = xi ; (q2)ij = xixj − xi xj ...)satisfanla relaciód’escalamentsegüent: qn(a) = n 1qn1(a) + nqn2(a) + O( n+1),on = Ω 1.Aquestescalament,alseutorn,dónallocaundesenvolupament asimptòticconsistentqueportaaunsistemad’equacionsdiferencialsordinàriesperalscumulants qn(a) entermesdetotselscumulantsd’ordreinferior, q1(a),...,qn 1(a)

L’escalamentmencionatperalscumulantsd’ordre n implicaqueespotobtenirunaaproximaciógaussianadelprocéstalque X(t) = ΩN (q11, Ω 1/2q21), on q11(a) ésl’aproximaciód’ordremésbaixperalprimercumulant(ésadir, elprimermoment, q1),quesatisfàlesequacionsdecampmitjà[3,30]:

q11 = i riwi(q11(a),a), (2.6)

i q21(a) ésl’aproximaciód’ordremésbaixperalsegoncumulant(ésadir, lamatriudecovariància, q2(a)),elscomponentsdelqualsatisfanelconjunt d’EDO:

Qij (a) = k Qik

on Qij ≡ (q21)ij .PeramésdetallssobreelmètodeWKB,inclosal’obtenció detalladadel’equació(2.6),vegeu[3,30].

Usemlesequacions (2.6) i (2.7) performularelssistemesd’EDOperales contribucionsd’ordredominantperalprimerielsegoncumulants(i.e.,el primerielsegonmoment,respectivament).Substituintelsvalorscorresponents de w(→ x,r,a) i r delataula1al’equació (2.6),on q11 = → x = x éselvector mitjana,obteniml’equaciósegüentperacadaelementdelvectormitjana,on, fentunabúsdenotació,posem xi = xi:

Modelsestocàsticsmultiescaladepoblacionscel.lulars 139

Demanerasimilar,utilitzantl’equació (2.7),obtenimelconjuntd’EDO corresponent,elqual,acoblatamblesequacions (2.8),enspermetobtenirles entradesdelamatriudecovariància, σ(a) = (Qij (a))

Lafigura3mostralacomparacióentrelasoluciónumèricadel’equació (2.8) ilasimulaciódirectadelsistemaestocàsticusantl’algorismedeGillespie[20].

ParàmetreValor

a1

Font

0.04TysoniNovak(2001)[58]

a2 1TysoniNovak(2001)[58]

a3 0.25Alarcón etal. (2004)[1]

a4 0.04TysoniNovak(2001)[58]

b3 10TysoniNovak(2001)[58]

b4 35TysoniNovak(2001)[58]

η 0.01TysoniNovak(2001)[58]

m 10TysoniNovak(2001)[58]

J3, J4 0.04TysoniNovak(2001)[58]

u 1TysoniNovak(2001)[58]

cz1 0.1Alarcón etal. (2004)[1]

cz2 0.01Alarcón etal. (2004)[1]

B 0.01Alarcón etal. (2004)[1]

d1 (0.1 + d2)/(J3 s0)

d3 (0.01 + d4)/(J4 s0)

ν 10 4

k 0.067

κ 1.57 10 4

Taula 2: Valorsdelsparàmetres.

Finalment,aplicantelsresultatsprevisrelacionatsambelmètodeasimptòticWKBal’EM,obtenimunaaproximaciógaussianaalasoluciódel’equació(2.1):

on d éselnombred’espèciesquímiquesenelnostremodeldeciclecel lular; |·| denotaeldeterminant; () 1,lainversa; X(a) és q11,i σ(a) éslamatriude covariància(simètrica),amb Qij lessevescomponents.

Figura 3: Comparaciódelestrajectòriesde x(a) i y(a) obtingudes apartirdel’equació (2.8) (líniesgrisesclares)ilesobtingudesamb diferentssimulacionsdeGillespie.Aquestessimulacions,pera Ω = 105 , esrepresentenengris(100realitzacions,líniadeguions,iunasola realització,líniadepunts);pera Ω = 107,esrepresentenengrismés fosc(100realitzacions,líniadepuntsiguions,iunarealització,líniade senyals).Finalment,leslíniesdepuntsnegresmésexteriorsrepresenten l’error(±σ(a))quedónal’equació (2.7).S’hapres O2 = 1.0ilacondició inicial → x = (5, 1 4, 0 01, 0 01, 0, 0 99, 0 01, 0, 0 01)

2.3Modelitzaciódelataxadedivisióquedepèndel’edat

L’activaciódediversesviesderegulació,enparticular,elciclecel.lular,depènde siuncertcomponentdelsistemaderegulacióarribaaunvalorcríticd’activació. Enelcasdelnostresistemaestocàsticperalaprogressióenelciclecel.lular, lescèl.lulespassenperlatransició G1/Squanelnivelld’activitatdeCycBarriba aunvalorllindar.Suposemque,desprésquelacèl lulapassiaquestatransició, completaelciclecel.lulari,finalment,esdivideixdesprésqueuntempsmitjà τp hagitranscorregut.Pertant,atesescertescondicionsexternes(enelnostre

Modelsestocàsticsmultiescaladepoblacionscel.lulars 141

cas,aquestescondicionsestandeterminadesperlaconcentraciód’oxigen),la probabilitatd’unacèl.luladedividir-sedesprésd’unacertaedatésigualala probabilitatquelacorresponentproteïnahagiarribatalseuvalorcrític.Això potserformulatentermesd’unproblemadetempsdeprimerpas(vegeu[46]), lasoluciódelqualdónaaquestaprobabilitatdeformaprecisailasevaderivada respecteal’edatensdónalataxadedivisióaedat a.Uncophemobtingutla taxadedivisiócorresponentseguintaquestametodologia,podemutilitzar-la perparametritzarunaequaciómestraperal’evolucióestocàsticadelapoblació cel.lular.

Percalcularlataxadedivisió(ésadir,laprobabilitatdedivisiópercèllulaiperunitatdetemps)entermesd’unproblemadetempsdeprimer pas,consideremquelatransició G1/Socorrequanl’activaciódelaciclina arribaalvalorllindari,pertant,podemdefinirlataxadedivisiócomuna funciódeltemps,ésadir, b(a) = ∂a(1 G(a)) =− R ∂aΨ ( → X(a))d → X ,amb R ={y<k,(m,z,x1,e1,c1,x,e2,c2) ∈ Rd 1},on1 G(a) éslaprobabilitat quelaciclina-CDKestiguipersobredelseuvalorllindaral’edat a. G(a) = R Ψ ( → X(a))d → X ésl’anomenada probabilitatdesupervivència, i.e.,laprobabilitat que → X(a) ∈ R.Si Ψ ésaproximadaperl’equació (2.9),podemobteniruna equaciótancadapera G,entermesde G, x i Qij

Esteminteressatsenlaregióon y ésmésgranqueunaconstant, k,amb toteslesaltresvariablesvariantsobretotselsseusrangs.Pertant,enaquest cas,l’expressióde G esredueixa: G(a) = y<k

ij (matriudecovariànciacondicionada).

Pertant, G(a) potserreescritausantlafuncióerror,talcomsegueix:

Així,doncs,l’equacióperalataxadedivisiós’obtéderivantl’equacióde G a(2.10):

dG(a) da =− 1 2 d da σy (a) σy (a) G(a) + Ω y<k dφ(y) dy dy(a) da Ψ (y(a))dy+ + Ω d da σy (a) σy (a) y<k φ(y)Ψ (y(a))dy, (2.12) on φ(y) = 1 2 (y y(a))2σy (a) 1 . UtilitzantelteoremadeladivergènciaidesenvolupantperTaylor,laprimera integraldel’equació(2.12)queda: I1 = Ω 2πσy 1/2 dy(a) da e Ωφ(y) i 1 i! Ωiφ(y)i k −∞ = = Ω 2πσy 1/2 dy(a) da 1 e Ωφ(y) k −∞ ,

mentrequelasegonaintegraldel’equació (2.12) potseraproximadaestenent eldominid’integracióa ±∞: I2 = Ω d da σy (a) σy (a) 1 σ 1/2 y ∞ −∞ φ(y) Ω 2π 1/2 e Ω 2 (y y(a))2σ 1 y dy = = 1 2 d da σy (a) σy (a) .

Hemcomprovatmitjançantintegraciónumèricaquel’errorintroduïten canviareldominid’integració (y<k) per R a I2 ésnegligible. Finalment,podemconclourequel’EDOque G(a) hadesatisferés: dG(a) da =− 1 2 d da σy (a) σy (a) (G(a) 1) Ω 2πσy 1/2 dy(a) da e Ωφ(k) . (2.13)

L’equació (2.13),resoltaconjuntamentamblesequacions (2.8) i (2.7),dóna lataxadedivisiócomafunciódel’edatidelaconcentraciód’oxigen.

Lafigura4mostralaprobabilitatquelaciclina-CDKexcedeixielseuvalor llindar,1 G(a),usantl’equació (2.11) acobladaamblesequacions (2.8) i (2.7), icomparaelresultatambl’algorismedesimulacióestocàsticadeGillespie[20].

Alafigura5hemrepresentatlataxadedivisióperadiferentsconcentracionsd’oxigen.Compodemveure,elmàximvalorde b(a) ocorreatempsmés avançatsperaconcentracionsd’oxigenmenors.Aixòconfirmaquelafalta d’oxigenretardaqueocorrilatransició G1/S.Alafigura6s’observaquela probabilitatdedivisiótémésvariànciasiincrementemelsorollenelprocés.

Figura 4: Comparaciódediferentssolucionsdel’equació (2.11) i100realitzacionsdel’algorismedeGillespieamb Ω = 107 (línianegradeguions verticals).Lessolucionsdel’equació (2.11) esdonenpera Ω = 107 (línia depuntsiguions),108 (líniadeguions),109 (líniacontínua).S’hapres O2 = 1.0ilacondicióinicial → x = (5, 1.4, 0.01, 0.01, 0, 0.99, 0.01, 0, 0.01).

Figura 5: Equació (2.13):taxadenaixementperadiferentsconcentracionsd’oxigen,amb O2 = 0.05(líniadepuntsiguions,aladreta), O2 = 0 1(líniadeguions,alcentre), O2 = 1(líniacontínua).Pera Ω = 107 icondicióinicial → x = (5, 1.4, 0.01, 0.01, 0, 0.99, 0.01, 0, 0.01).

Figura 6: Comparaciódelessolucionsdel’equació (2.13) peradiferentsvalors: Ω = 107 (líniadepuntsiguions,mésplana),108 (línia deguions),109 (líniacontínua).S’hapres O2 = 1 0icondicióinicial → x = (5, 1.4, 0.01, 0.01, 0, 0.99, 0.01, 0, 0.01).

3Equaciómestraestructuradaperl’edatiaproximacióWKB

3.1Formulaciódel’equaciómestraestructuradaperl’edat Arajaestemendisposiciódeformularelnostremodelperaladinàmica poblacional.Utilitzantelcontextanterior,calculemlataxadenaixementcoma funciódel’edatcel.lular.Formulemunprocésdenaixement-mortquedepènde l’edat.Elsparàmetrescomlataxadedivisióquedepèndel’oxigenidel’edates determinenentermesdelsmodelsanalitzatsal’escalaintracel.lular,descritsa laseccióanterior.Perobtenirl’equaciómestraquedepèndel’edat,considerem laidentitatsegüent:

P(n(a),a + δa,t + δt) = W(n(a) + 1,a,t)δtP(n(a) + 1,a,t)+ + (1 W(n(a),a,t)δt)P(n(a),a,t), (3.1) on n(a,t) denotalapoblaciód’edat a altemps t ion W(n(a),a,t) = (ν + b(a))n(a),amblataxadedivisiódonadaper b(a) =− dG(a) da i ν éslataxade mortalitat,suposadaconstant.

Perclaredat,discretitzemlavariableedat a en It grups,demaneraqueles p0j divisionsaedat aj estandeterminadesperunavariablealeatòriadePoissonambmitjana(ivariància) λj = b(aj )n(aj )δt,distribucióquedenotarem per Pλj .Laprobabilitatde p0 divisionsenl’intervaldetemps (t,t + δt) pot serexpressadacomunasumadelesdivisionsatemps t enelsdiferentsgrups d’edat aj ,ésadir,totselspossibles p0j talsque p0 = j∈It p0j .Pertant,

Prob(p0) = P(n(0) = 2p0,t) = {p0j }j∈It

PPλj (p0j )

δ j p0j ,p0 , (3.2)

Modelsestocàsticsmultiescaladepoblacionscel.lulars 145

on PPλj (p0j ) = e λj λp0j j p0j ! denotalaprobabilitatquelavariabledePoissonde paràmetre λj = b(aj )n(aj )δt valgui p0j .Quanl’esdevenimentd’unadivisió ocorre,elnombredecèl.lulesambedat a = 0s’incrementaen2p0,mentreque elnombredecèl.lulesambedat a = aj disminueixen p0j

Reordenantl’equació(3.1)iprenentellímitquan δt → 0,obtenim:

∂P(n,a,t) ∂t + ∂P(n,a,t) ∂a = W(n(a) + 1,a,t)P(n(a) + 1,a,t)

W(n(a),a,t)P(n(a),a,t).

(3.3)

Pertaldetrobarunasolucióaproximadadel’equació (3.3),apliquemel mètodeWKBproposatperKubo etal. a[30],onesmostraquelestaxesde transició W(n,a,t) handeserfuncionshomogèniesde n pertald’obtenir unasoluciódel’EMdelaforma P(n(a),a,t) = C exp( Ωs(n(a),a,t)),amb n(a) = n(a)/Ω: W(n(a),a,t) = Ωw(n(a),a,t). (3.4)

D’acordambaixò,laprobabilitatquepassiunacertareaccióenunintervalinfinitesimaldetempsésproporcionalalamidadelsistemainomésés determinadaperl’estatdelsistema,representatpelconjuntdelesvariables intensives n(a).Ladefinició

P(n(a),a,t) = ΩP(n(a),a,t), juntamentambl’equació (3.4),faquel’equació (3.3) tinguil’expressiósegüent:

1 Ω ∂P(n,a,t) ∂t + ∂P(n,a,t) ∂a = (ν + b(a))(n(a) + 1)P(n(a) + 1,a,t) (ν + b(a))n(a)P(n(a),a,t), laqualcosaenspermetescriurel’EM(3.3)enformaWKB:

1 Ω ∂P(n,a,t) ∂t + ∂P(n,a,t) ∂a = = e1/Ω(∂/∂n(a)) 1 w(n(a),a,t)P(n(a),a,t), (3.5)

onhemutilitzatque e (∂/∂n(a)) éselgeneradordelestranslacionsal’espai d’estatsdelsistema.

Consideremaralafunciógeneratriudecumulants,definidacom q(u,a,t) = log(Q(u,a,t)),on Q(u,a,t) éslafunciócaracterísticade P(n,a,t),definida comlasevatransformadadeFourier:

Q(u,a,t) = +∞ −∞ ei unP(n,a,t)dn.

Elscumulants, qk(a,t),espodenobtenirapartirde q(u,a,t),comels coeficientsdeldesenvolupament:

q(u,a,t) = ∞ k=1 ik k! ukqk(a,t). (3.6)

Elprocedimentqueseguimacontinuació,queestàbasatenlafeinade Kubo etal. a[30],ésescriureunaequaciópera Q(u,a,t) iconstruirdesenvolupamentsasimptòticspera Q(u,a,t), q(u,a,t) i qk(a,t).Aquestesaproximacionsdonaranllocasistemesd’EDOperalscumulantsiperalsmomentsde lasoluciódel’EM.Esteminteressatsenelsistemad’equacionsperalprimer moment(q1(a,t))iperalselementsdelamatriudecovariància(q2(a,t)),que enspermetranestudiarelcomportamentmitjàdelsistemailesfluctuacions gaussianesalseuvoltant.

Perobtenirl’equaciópera Q(u,a,t),prenemlatransformadadeFourier del’EM,equació(3.5):

1 Ω ∂Q(u,a,t) ∂t + ∂Q(u,a,t) ∂a =

ei un e1/Ω(∂/∂n(a)) 1 w(n(a),a,t)P(n(a),a,t)dn. (3.7)

Laintegraldelcostatdretdel’equació(3.7)és:

ei un e1/Ω(∂/∂n(a)) 1 w(n(a),a,t)P(n(a),a,t)dn =

ei unw(n,a,t)P(n,a,t)dn. (3.8)

Amés,substituintl’equació (3.8) al’equació (3.7),reordenanttermesi recordantquelatransformadadeFourierdelproductededuesfuncionsés igualalaconvoluciódelestransformadesdeFouriercorresponents,obtenim finalment: 1 Ω ∂Q(u,a,t) ∂t + ∂Q(u,a,t) ∂a = = 1 2π (ei u Ω 1)

Q(u v,a,t)ω(v,a,t)dv, (3.9) on ω(v,a,t) ésunatransformadadeFourierde w(n,a,t)

L’equació (3.9) necessitasercomplementadaambcondicionsdefrontera pera P(n,a = 0,t),ésadir,perlaprobabilitatqueelnombrededivisionsen l’intervaldetemps (t,t + δt) sigui p0 = n/2.Talcoml’hemexpressata (3.2),el nombrededivisionsenaquestintervaldetempspotserescritcomunasuma deles p0j divisionsatemps t enelsgrupsd’edat aj ,ésadir,

P(n = 2p0,a = 0,t) = {p0j }

j PPλj (p0j )

δ j p0j ,p0 ,

Modelsestocàsticsmultiescaladepoblacionscel.lulars 147

on Pλj ésunadistribuciódePoissondeparàmetre λj = b(aj )n(aj )δt i PPλj (p0j ) denotalaprobabilitatqueaquestavariablevalgui p0j :

PPλj (p0j ) = e λj λp0j j p0j ! ,

i,enconseqüència,lacorresponentfunciógeneratriudecumulantsperlavariablealeatòria p0j és Qj (s) = eλj (eis 1).Ara,comque P(p0) ésunaconvolució, lafunciógeneratriudecumulantspera P(p0), Q(s,a = 0,t),estàdeterminada per[24]:

Q(s,a = 0,t) = j Qj (s) = e j b(aj )n(aj )(eis 1)δt ,

que,prenentellímitquan δt → 0,dóna:

Q(s,a = 0,t) = e ∞ 0 (eis 1)b(a)n(a)da . (3.10)

3.2AnàlisiWKBdel’equaciómestraestructuradaperl’edat Uncophemformulatlanostraequaciómestraestructuradaperl’edat,o, mésaviat,elproblemaequivalentperalacorresponentfunciógeneratriu, equacions (3.9) i (3.10),podemduratermelasevaanàlisiWKB[3, 30].Abans decontinuar,recordemque Q(s,a,t) estàrelacionadaamblafunciógeneratriu delscumulants, q(s,a,t): Q(s,a,t) = exp(q(s,a,t)),unarelacióquepotser reexpressadacom:

Q(u v,a,t) = eq(u v,a,t) = exp

ei u Ω 1 exp

k=0 ik k! ukq(k)( v,a,t)

, (3.11) on q(u v,a,t) haestatreemplaçadaper q(u v,a,t) = eu∂v q( v,a,t) i q(k)( v,a,t) ≡ (∂u)kq(u,a,t)|u=−v .Usantl’equació (3.11),l’equació (3.9) es converteixen: 1 Ω ∞ k=1 ik k! uk ∂qk(a,t) ∂t + ∂qk(a,t) ∂a = = 1 2π ei u Ω 1 ∞ −∞ Q(u v,a,t) Q(u,a,t) ω(v,a,t)dv = = 1 2π

∞ j=1 ij j! uj hj ( v,a,t)

eq( v,a,t)ω(v,a,t)dv

. (3.12)

Perconveniència,hemdefinitlaquantitatsegüent: hj ( v,a,t) ≡ ij (q(j)( v,a,t) q(j)(0,a,t))

ihemutilitzatque q(0)( v,a,t) = q( v,a,t)

Centrem-nosaraenelprimercumulant q1(a,t) = n(a,t) ,queestàdeterminatpelstermes O( ) al’equació (3.12).Desenvolupantlesexponencialsdel costatdretdel’equació (3.12) iconservantnoméselstermesdeprimerordre, obtenim:

∂q1(a,t) ∂t + ∂q1(a,t) ∂a =− 2

eq( v,a,t)ω(v,a,t)m0( ,v,a,t)dv, (3.13)

on ≡ Ω 1 i mk( ,v,a,t) estàdefinidaper:

L’equació (3.13) hadeserequilibradacorrectamentrespectedelpetitparàmetre .Aquestequilibris’aconsegueixsi,al’ordredominant, m0( ,v,a,t) = O( 0),que,defet,sesatisfà,jaque m0( ,v,a,t) = 1(vegeul’equació (3.14))i q1(a,t) = O( 0).

Repetintelmateixperalsegoncumulant, q2(a,t),obtenim: 2 ∂q2(a,t) ∂t + ∂q2(a,t) ∂a = = 1 2

m1( ,v,a,t)+ 2 2 m0( ,v,a,t) eq( v,a,t)ω(v,a,t)dv. (3.15)

Equilibrantl’equació (3.15),s’obtél’escalamentsegüental’ordredominant: q2(a,t) = O( ) i m1( ,v,a,t) = O( ).Espotcomprovarqueaquestesrelacionsd’escalamentsóncoherentsambl’equació(3.14).

Engeneral,podemveurequelasubstituciód’escalament qk(a,t) = k 1qk1(a,t) + kqk2(a,t) + O( k+1), mk( ,v,a,t) = kmk1(v,a,t) + k+1mk2(v,a,t) + O( k+2),

éscoherentambl’equació (3.14) iportaaequacionsequilibradesperalscumulants qk(a,t)

Aordredominant,l’equaciópera q1(a,t) ésdelaforma:

∂q1(a,t) ∂t + ∂q1(a,t) ∂a =− 1 2π ∞ −∞ eq( v,a,t)ω(v,a,t)dv, (3.16)

mentrequel’equaciócorresponentpera q2(a,t) és: 2

∂q2(a,t) ∂t + ∂q2(a,t) ∂a = = 1 2π ∞ −∞ m1( ,v,a,t) + 2 2 eq( v,a,t)ω(v,a,t)dv. (3.17)

Modelsestocàsticsmultiescaladepoblacionscel.lulars 149

L’aproximacióal’ordredominantdel’equació (3.17) s’obtédelamanera següent.Delesdefinicionsdelesquantitats hj i mj ,n’obteniml’expressió següentpera hj : hj ( v,a,t) = i j ∞

Pera j = 1,del’equació (3.14),deduïmque m1 = h1.Tenintencompte lasubstituciód’escalamentde mk i qk,obteniml’aproximaciód’ordre O( ) següent:

Pertant,substituintl’equació (3.18) iquedant-nosnomésamblescontribucionsdel’ordredominant,l’equaciópera q21(a,t) quedaaixí:

∂q21(a,t) ∂t + ∂q21(a,t) ∂a = 1 2

ivq21(a,t) + 1 eq( v,a,t)ω(v,a,t)dv.

Amésamés,lasubstituciód’escalamentpera qk(a,t) il’equació (3.6) portena:

q(u,a,t) = 1 ρ( ,u,a,t),

ρ( ,u,a,t) = ∞ j=1 ∞ k=1 ij j!

(a,t) (3.19)

Aixòpràcticamentcompletalanostradeducciódelesequacionsd’evolució pera q1(a,t) i q2(a,t).Al’ordredominant,l’equació (3.19) potserreescrita coma:

ρ( ,u,a,t) = ρ1(u,a,t) + O( 2), (3.20)

ρ1(u,a,t) = iuq11(a,t). (3.21)

Substituintlesequacions (3.20) i (3.21) al’equació (3.16),obtenimque,a l’ordredominant,lesequacionspera q11(a,t) i q21(a,t) sónlessegüents:

∂q11(a,t) ∂t + ∂q11(a,t) ∂a =− 1 2π ∞ −∞ eq( v,a,t)w(v,a,t)dv = c(q11,t), on w(v,a,t) éslatransformadadeFourierde w(n,a,t) i,pertant,tenim c(q11,t) =−(ν + b(a))q11. Finalment,l’equaciód’evoluciópera n(a,t) = q11(a,t) és:

∂n(a,t) ∂t + ∂n(a,t) ∂a =−(ν + b(a))n(a,t),

n(0,t) = 2 ∞ 0 b(a)n(a,t)da, (3.22)

mentrequel’equacióperalavariànciai σn(a,t) = q21(a,t) és:

∂σn(a,t) ∂t + ∂σn(a,t) ∂a = (ν + b(a))σn(a,t) (ν + b(a)), σn(0,t) = 4 ∞ 0 b(a)n(a,t)da.

3.3Aproximaciógaussianaperalmodelestocàsticmultiescala

Desprésdelscàlculsdelesseccionsanteriors,arajapodemescriurel’aproximaciógaussianaperalmodelmultiescalarepresentatesquemàticamentala figura1.Elsistemaacoblatquedeterminaaquestaaproximacióéselsegüent:

• Concentraciód’oxigen, O2: dO2 dt = S κO2M, on M(t) = ∞ 0 n(a,t)da, (3.24)

on O2 éslaconcentraciód’oxigenconsumidaperlapoblaciótotal, M(t); S éslataxadedistribuciód’oxigenalapoblació,laqualnosaltressuposemconstant,i κ éslataxadeconsumd’oxigenpercèl.lula,laqual suposemqueésindependentdel’edat.

• Taxadedivisióquedepèndel’edatidel’oxigen(secció3): ˙ x = i riwi(x(a),r,a,O2),

˙ Qij (a) = k Qik

∂cj (x,a) ∂xk + ∂ci(x,a) ∂xk Qkj + r rirj w(x,r,a,O2), (3.25)

b(a) = dG(a) da =− 1 2 d da σy (a) σy (a) (G(a) 1) Ω 2πσy 1/2 dy(a) da e Ωφ(k) .

• Mitjanaivariànciadelapoblacióestructuradaperl’edat(subseccions3.1 i3.2):

∂n(a,t) ∂t + ∂n(a,t) ∂a =− (ν + b(a))n(a,t), n(0,t) = 2 ∞ 0 b(a)n(a,t)da, (3.26)

∂σn(a,t) ∂t + ∂σn(a,t) ∂a = (ν + b(a))σn(a,t) (ν + b(a)),

σn(0,t) = 4 ∞ 0 b(a)n(a,t)da.

4Esquemanumèric:mètodedesalt τ quedepèndel’edat

Enaquestasecció,descrivimunmètodenumèricestocàsticpercompararla soluciódel’EM (3.3)–(3.2) amblessolucionsdel’aproximacióWKBdonadespel sistemad’equacions(3.24)–(3.26).

Utilitzemunaextensiódelmètodedesimulaciódesalt τ enelprocés naixement-mortdescritperl’EM (3.3)–(3.2),onlaprobabilitatdedivisióestà determinadaperl’equació (2.11).Utilitzantunsalt τ acadagrupd’edat ai presentalapoblació,generemunpasdetempsacadaedat, τi.Elpasdetemps global, τ,estriadeformaquesiguielmínimdels τi peratot i.Arribatsaaquest punt,podemcalcularelnombred’esdevenimentsdivisióiesdevenimentsmort queocorrerandurantellapsedetemps τ acadagrupd’edat ai,quesón modelatsperdistribucionsdePoisson P(dij τ),on:

di1 = b(ai)n(ai),

Lesigualtats (4.1) i (4.2) donenlesprobabilitatsdedivisióidemortdurantun (petit)intervaldetempsdedurada τ peracèl.lulesd’edat ai.Elsesdeveniments ambprobabilitatsdonadesper (4.1) i (4.2) produeixencanvisassociatsala població n(ai) donatsper ri1 =−1i ri2 =−1,respectivament.Addicionalment, unesdevenimentdivisió(laprobabilitatdelqualésdonadaper (4.1))téun canviassociatalescèl.lulesnounades,ésadir,alescèl.lulesambedat a = 0, donatper r0 = 2.

Primer,introduiremelmètodeiexplicaremcomgeneralitzar-loalnostre problemaestructuratperl’edat.Després,procediremadescriurel’algorisme usatenlesnostressimulacions.

4.1Mètodedesalt τ estructuratperl’edat

Enaquestasecció,explicaremelmètodedesalt τ descrita[12, 21]ilamodificacióquenosaltresn’hemfet.L’algorismedesimulacióestocàsticade Gillespie(SSA)[20]proporcionarealitzacionsexactesdeladensitatdeprobabilitatqueresolenl’equaciómestracorresponent.Peraconseguir-ho,elque fal’algorismeésduratermetotselsesdevenimentsenelcamídemostra, laqualcosasignificaqueaquestmètodepotsermoltlent,enparticular,per asistemesqueinvolucrinprocessostantràpidscomlents.L’algorismede simulacióestocàsticaSSAtambégeneraunagranquantitatd’informaciódetalladadecadacamímostral,elconeixementdelaqualpotserinnecessarien moltesaplicacions.Envistad’aquestasituació,elmètodedesalt τ [21]vaser proposatambl’objectiud’accelerarlasimulaciódelsprocessosdeMarkov,la qualcosaresponalaqüestiósegüent:ambquinafreqüènciaesprodueixcada procésenl’intervalsegüentdetempsespecificat τ?Elfonamentmatemàtic d’aquestalgorismepotremuntar-seal’anomenada representaciódelsprocessos deMarkov.Mésespecíficament,suposemunprocésdeMarkov, X(t),ladensitat

deprobabilitatdelqualsatisfàl’equaciómestra:

dΨ (X,t) dt = i (Wi(X ri,t)Ψ (X ri,t) Wi(X,t)Ψ (X,t)). (4.3)

Cadareacció i,involucradaenelprocésdescritperl’equació (4.3),està caracteritzadaperunadistribuciódetempsd’esperaexponencial[20]:

Pi(tw | X(t)) = Wi(X,t)e tw /Wi(X,t) .

Pertant,sabemqueelnombredevegadesqueelcanal i ésutilitzaten l’intervaldetemps (0,t) és P t 0 Wi(X,s)ds ,on P(λ) ésunnombrealeatori ambdistribuciódePoissonambparàmetre λ;vegeu[24].Aleshores, X(t) es potrepresentarformalmentcom:

X(t) = X(t = 0) + i riP t 0 Wi(X,s)ds .

UtilitzantlapropietatdeMarkov, X(t + τ) potserexpressatentermes de X(t) com:

X(t + τ) = X(t) + i riP t

Així,doncs,laqüestióqueelmètodedesalt τ preténrespondrepotserreformuladadelaformasegüent:sotaquinescondicionsl’equació (4.4) potser aproximadaper

X(t + τ) X(t) + i riP (Wi(X,t)τ).

Ditd’unaaltramanera,necessitemestimar τ deformaque t+τ t Wi(X,s)ds Wi(X,t)τ.Aquestésunproblemaperalqualencaranoesconeixcapsolució sistemàtica.Encanvi,s’handonatdiversesestimacions,conegudescoma condicionsdesalt,sotacerteshipòtesis[12, 21].Agranstrets,podemdirque τ necessitasertriatdeformaque |Wi(X,t) + ki) Wi(X,t)| siguiacotatper unaquantitatpetita.

Pertaldegeneralitzaraquestmètodealnostremodelestructuratperl’edat, consideremprimerunvectord’edats,lescomponentsdelqualsón n(ai) amb i ∈ It ,on It esmouenelconjuntdelesedatspresentsalapoblacióa l’instant t,ésadir,deformaque n(ai)> 0atemps t.Elprimerproblemaés triarunvalorpera τ quesatisfacilacondiciódesalt.Lageneralitzaciómés simpledel’algorismedesalt τ estàndardéstriarunvalordesalt, τi,pera cadaedat, ai,amb i ∈ It ,d’acordambelcriteriestablerta[12],idespréstriar elmínimentretotsells.

Comencemcalculanteltemps, τi,peracadaedat, ai,amb i ∈ It ,utilitzant elmètodeformulatperCao etal. a[12],quemilloraelsresultatsprevisde GillespieiPetzolda[22],jaques’ajustamilloralacondiciódesalttotacotant

Modelsestocàsticsmultiescaladepoblacionscel.lulars 153

uniformementelscanvisrelatiusenlesfuncionsdetendència.Amésamés, aquestmètodeésmésràpidqueelprocedimentsuggerita[22],jaqueel nombredepassosauxiliarsutilitzatspercalcularelsaltdetempss’incrementa linealmentambelnombred’espèciesreactants,enllocdefer-hodeforma quadràticaambelnombredecanalsdereacció[12].

L’estratègiadarrered’aquestprocedimentdeselecciódels τi ésacotar elscanvisrelatiusenelnombred’individusdelespoblacions,deformaqueels canvisrelatiusenlesfuncionsdetendènciasiguintotsaproximadamentacotats perunvalorespecífic (0 < < 1).Sigui

Laseleccióde τ l’hemdebasarenlacondició

on Jrs denotaelconjuntd’índexsdetotalapoblacióambedatdiferent(osigui, i ∈ Jrs siinoméssi dij ésl’argumentdecomamínimunafunciódetendència).

ComquelesvariablesaleatòriesPoisson P(dij τi) delcostatdretdel’equació (4.5) sónestadísticamentindependentsitenenmitjanesivariàncies dij τi, lamitjanailavariànciadelacombinaciólinealdel’equació (4.5) podenser calculadesfàcilment,

i)

UtilitzantelmateixraonamentqueesvaferservirenladerivaciódelprocedimentdeGillespieiPetzoldperalaseleccióde τ [22],nosaltresconsiderarem quelacota (4.6) de ∆τi n(ai) seràsatisfetasubstancialment,siéssatisfeta simultàniamentperlamitjanaabsolutailadesviacióestàndardde ∆τi n(ai):

Substituintlafórmula (4.7) alescondicions (4.8),obtenimlescotessegüents pera τ τi ≤

Arribatsaaquestpunt,hemcomputatelsaltdetempsperacadaedat, τi. Pertaldeferavançarelsistemaentemps,prenemelmínim τi quesatisfàla condiciódesaltcorresponent,

icalculemlesquantitats kij =P(dij τ) i λi = j kij .Finalment,femefectiu

elsalt,demaneraquereemplacem t per t + τ i n(ai) per n(ai) λi.Si ki1 =P(di1τ) noészeroperaunacertaedat i,significaqueenlapoblació d’edat ai hihahagutdivisionsi,consegüentment,lapoblaciód’edatzero és n(0,t + τ) = 2 i P(di1τ).Això,alseutorn,tambéimplicaqueelvector numèricd’edatstéaraunanovacomponent,ésadir, It+τ = It + 1.

Percalcular di1,necessitemsaberelvalordelataxadedivisió, b(ai),al noutemps t + τ.Peraixò,resolemelsistema (3.24)–(3.25) enl’intervalde temps (t,t + τ) peracadaedatutilitzantelvector → n(ai).Perfer-ho,hem utilitzatunmètodeimplícitRunge-KuttadesegonordreimplementatalaGNU ScientificLibrary(GSL).Ara,doncs,tenimlaprobabilitatdedivisióatemps t. Utilitzantl’equació (2.11),obtenim1 G(ai)t atemps t.Així,calculemlataxa dedivisióperacadaedat:

b(ai) = (1 G(ai)t ) (1 G(ai)t+τ ) τ

4.2Descripciódel’algorisme

L’algorismedesimulacióés:

1. Inicialització.Començarambunvectord’edatsinicial, → n(a, 0) a t = 0,les componentsdelqual, n(ai, 0),donenlapoblaciócorresponentacada grupd’edatpresentalapoblacióinicial.Ladimensiód’aquestvectores denotaper I,icorresponalnombredegrupsd’edatambpoblacióinicial diferentdezero.A t = 0, b(ai) = 0peraqualsevoledat.

2.Computarlestaxesdedivisióidemortalitatperacadaedat: di1 = b(ai)n(ai) i di2 = νn(ai)

3. Determinarelsaltdetemps τ,d’acordamblacondiciódelsalt(vegeula subsecció4.1).

4.Actualitzarlesvariablesdelsistema: → n(a,t) ← → n(a,t) (P(di1τ) +P(di2τ))i∈I , t ← t + τ, a ← a + τ.

5. Determinarelnombredenaixements: n(0,t) = 2 i P(di1τ).Sielnombre denaixements n(0,t) ésdiferentdezero,hemd’afegirlanovacomponent alvectordistribuciód’edats,ésadir, I ← I + 1.

6. Resoldrel’equacióperalaconcentraciód’oxigenal’interval (t,t + τ): ∂t O2 = F κO2M,on M(t) = i n(ai,t) éslapoblaciótotal.

7. Calcularlestaxesdedivisió, b(ai),usantlesprobabilitatsdedivisióa temps t:usantl’equació (2.11),obtenim1 G(ai)t atemps t i,aleshores, calculemlataxadedivisió, b(ai) = (1 G(ai)t τ ) (1 G(ai)t ) τ .

8.Bucledel’ítem2al7finsque t ≥ T .

Figura 7: Unarealització(entraçdeguionsverticals)i100realitzacions(enlíniagrisadeguionsipunts)del’algorismedesimulació desalt τ del’equació (3.3)–(3.2) amb Ω = 103,i,també,unarealitzacióengrisclargruixuti100realitzacionsenlíniagrisaclara delmateixalgorismeamb Ω = 107,comparadesamblasolucióde l’equació (3.22) (líniadeguionsgrisa)amberrorcalculatusantl’equació (3.23) (líniesdeguionsnegres),amb Ω = 104 icondicióinicial → x = (5, 1 4,

Figura 8: Comparaciódelconsumd’oxigenutilitzant100realitzacionsdel’algorismedesimulaciódesalt τ del’equació (3.3)–(3.2) per a Ω = 103 (líniadeguionsipuntsgrisa)ipera Ω = 107 (líniagrisaclara)ambelconsumd’oxigenques’obtéusantl’equació (3.22) (líniadeguions),amb Ω = 104 , ν = 0 0001icondicióinicial → x = (5, 1.4, 0.01, 0.01, 0, 0.99, 0.01, 0, 0.01).

Figura 9: Comparaciódelnombredenaixementsutilitzant100realitzacionsdel’algorismedesimulaciódesalt τ del’equació (3.3)–(3.2) per a Ω = 103 (líniadeguionsverticalsgrisafosca)ipera Ω = 107 (línia grisaclara)ambelsnaixementsques’obtenenusantl’equació (3.22) (n(0,t) éslalíniadeguions),amb Ω = 104 , ν = 0.0001icondicióinicial → x = (5, 1 4, 0 01, 0 01, 0, 0 99, 0 01, 0, 0 01)

Elsresultatsdelessimulacionsusantaquestalgorismeespodenveureales figures7i9,onl’algorismedesimulaciódesalt τ estructuratperl’edatescomparaamblasoluciónumèricadelsistemad’equacions (3.22),pertaldevalidar l’aproximacióWKB-gaussiana.L’aproximaciógaussianadelesequacions (3.22) implicaqueel68.2%delesrealitzacionshauriad’estardinsdelaregiódelimitadaperlescotessuperioriinferiordonadesper n(t,a) ± Ω α0/2σn(t,a). Lafigura7mostraquelesrealitzacionsestocàstiquesgeneradespelnostre algorismeestanentrelescotesprevistesperal’aproximaciógaussiana.

5Conclusionsidiscussió

Enaquestarticle,presentemunaformulaciód’unmodelestocàsticmultiescala deladinàmicadelespoblacionscel lularsonnivellsd’organitzacióbiològica diferents,caracteritzatsperescalestemporalsdiferents(vegeulafigura1), estanacoblats.Descrivimladinàmicaestocàsticadelapoblaciócel lular(escala cel.lular,usantlamateixaterminologiaquea[2])mitjançantunprocésde naixementimortonlataxadedivisióésdescritaperunmodeldeprogressióen elciclecel lularreguladaperl’oxigen(escalaintracellular,usantlaterminologia de[2]),i,pertant,acoblemlesescalescel.lulariintracel.lular.Elsistemaacoblat resultantésunapoblaciócel lularestocàsticaestructuradaperl’edat.Lataxa

Modelsestocàsticsmultiescaladepoblacionscel.lulars 157

dedivisióesdescriuentermesd’unnoumètodebasatenunenfocamentde tempsmitjàdeprimerpas,elqualenspermetdeterminarlataxadedivisió comlataxamitjanaalaquallesproteïnesclauinvolucradesenlaregulaciódel ciclecel.lularcreuenelvalorllindard’activacióenfunciódel’edatcel.lular(ésa dir,eltempsquehatranscorregutdesdeladarreradivisiócel.lular).Lanostra metodologia,pertant,enspermetanalitzarl’acoblamententrelesfluctuacions causadespersorollmolecularanivellintracel.lularielsorollcel.lularacausa delamidafinitadelapoblació.

Ambl’objectiud’analitzarelcomportamentdelnostremodel,alasecció3, hemestèsunmètodeasimptòticdetipusWKBinicialmentproposatperKubo etal. [3, 30]perobtenirunasolucióaproximadadel’equaciómestra (3.5) de naixementimortestructuradaperl’edat.Duentatermeaquestaaproximació aunordremenor,obtenimunaaproximaciógaussianaperaladensitatde probabilitat(estructuradaperl’edat),onlamitjanacorresponent, n(a,t),ila variància σn(a,t) sónlessolucionsdeduesEDPsemilinealsacoblades(vegeu lesequacions(3.24)–(3.26)).

LesEDPsemilinealspera n(a,t) i σn(a,t) estanacobladesaescalaintracellularatravésdelasevadependènciadelataxadedivisió(quedepèndel’edat), b(a,t).Aquestaquantitats’obtéentermesdeltempsmitjàdeprimerpasperal modeldelciclecel lularquedepèndel’oxigen(elsdetallsesdonenalasecció2): consideremquelacèl.lulaentraenlafasedeproliferaciódelciclecel.lularquan laconcentraciódeCycBestàpersobred’unvalorllindardeterminat.Lataxa dedivisió,pertant,ésdonadaperlataxaalaqualelsistemacreuaelvalor llindaresmentatanteriorment.Pertalderesoldreaquestproblema,duema termeunaaproximacióWKB[3, 30]del’equaciómestracorresponent(vegeu l’equació (2.1) ilataula1)perobtenirunaaproximaciógaussiana,laqualestà determinadaperlasoluciódelsistemad’EDOperalamitjana, (2.6),ipera lavariància, (2.7).Això,alseutorn,enspermettrobarunaaproximacióala soluciódelproblemadetempsmitjàdeprimerpasi,pertant,alataxade divisióquedepèndel’edat.

Lanostraformulacióperalaprogressiódelciclecel.lularreguladaper l’oxigenésdescritapeltempsmitjàd’activaciódeprimerpas.L’aproximació peraladivisióescalculausantlaprobabilitatquelaciclina-CDKestiguiper sotad’unvalorllindar,quecorresponalaprobabilitatd’extinció,equació (2.10), deformaqueelprocésdereproduccióocorreambprobabilitatcomplementàriad’aquella.Percalcularelprocésd’activació,hemusatelmètodeWKBper obtenirunasolucióaproximadaal’EMdelciclecel lular.Aquestresultatésuna sèriedesistemesd’EDOperalscumulantsd’ordre n;hemusatordre2per obtenirunasoluciódel’EM, (2.9).D’acordamblacomparacióentreelsresultats delnostremodelreduïtilessimulacionsdeGillespie,podemafirmarqueel nostreenfocamentésunabonaaproximaciónomésperasorollintracel.lular petitimidagrandelsistema,d’ordre Ω = 107 osuperior(vegeulafigura3). Perobtenirunaaproximaciómillor,hemd’utilitzarunordremésgranque2en

l’aproximacióWKB.Elsistemas’acoblaatravésd’unmecanismederetroalimentaciónegatiu,onlapoblacióconsumeixoxigenque,alseutorn,regulala progressiódelciclecel lulari,pertant,lataxadedivisió.

Pertaldevalidarelnostreenfocamentasimptòticenelmodelestocàstic multiescala,hemintroduïtunaextensióestructuradaperl’edatdelmètodede simulaciódesalt τ enelprocésnaixement-mortassociatalesequacions (3.3)–(3.2),amblataxadedivisiócalculadaambl’equació (2.11).Comparemels resultatsdelessimulacionsestocàstiquesambl’aproximacióWKBdeladinàmicadelapoblaciócel.lularestructuradaperl’edatalafigura7,onespoden veurerealitzacionsdelprocésgeneradesutilitzantelnostremodeldesalt τ estructuratperl’edatambl’aproximacióasimptòticagaussiana.Alafigura8 hirepresenteml’evoluciótemporaldelaconcentraciód’oxigen,ialafigura9hi mostremelnombredenaixementsperl’aproximacióasimptòticailessimulacionsestocàstiques.Aquestacomparacióenspermetavaluartantlaprecisió comelrangd’aplicabilitatdelnostremètodeasimptòtic.Elsnostresresultats confirmenque,peralmodelintracel lularconsideratenaquestarticle,l’aproximacióasimptòticaésprecisanoméssiconsideremquel’escalaperalnombrede proteïnesalmodeldelciclecel lularintracel lular, Ω,siguiprougran.Enaquest cas,comespotveurealesfigures7,8i9,trobemquelaconcordànçaentre elsresultatsnumèricsiasimptòticsésbona.Aquestalimitaciópelquefaal nombredeproteïnesprovédelfetque,enelmodeldelciclecel.lularconsiderat enaquesttreball,latransicióqueanuncial’inicidelaproliferació(ésadir,quan CycBarribaalvalorllindar)estàprecedidad’unabifurcaciósella-node.Aprop d’aquestatransiciódefasedinàmica,s’esperaquel’aproximaciógaussiana siguiincapaçdecapturarlesestadístiquesdelesfluctuacions[8].Així,doncs, pertaldecapturarladinàmicadelsistemaambprecisió,ensmouremnomés enelrègimdelesfluctuacionspetites(i.e., Ω gran).Aixòsignifica,però,que elnostremodelseriacapaçdecapturarelcomportamentdesistemesqueno exhibissinaquesttipusdebifurcacionsenunrègimmoltmésampli.

UnaalternativaalmètodeWKBusatenaquestarticleseriaferservireldesenvolupamentdelamidadelsistemadeVanKampen[60],tambéconegudacom aproximaciódelsorolllineal (LNA),queestàmoltrelacionadaambl’aproximació WKBdeKubo etal. [30].Malgratlessimilitudsentreambduesmetodologies, aquestesnosónbenbéequivalents.L’aproximaciódelsorolllineal(LNA)suposa quelavariablealeatòriapotserescritacoma X(t) = φ(t) + Ω1/2ξ(t),on φ(t) éslasoluciódelesequacionsdecampmitjài ξ(t) ésunavariablealeatòria quesatisfàunaequaciódeFokker-Plancklineal,d’onpodenserdeduïdesequacionsdiferencialsordinàries(lineals)peralprimerielsegonmomentde ξ(t). L’aproximacióWKBestàbasadaenunAnsatzsobrelaformadelasolucióde l’EM,laqualcosasignificaque,pelquesabemapartirdelsnostresresultats, lesequacionsperalavariànciade X(t) nosón,engeneral,lesmateixes,toti ques’obtéenambdóscasoslamateixaaproximaciódecampmitjà.

Modelsestocàsticsmultiescaladepoblacionscel.lulars 159

Lametodologiapresentadaenaquestarticleespotgeneralitzardediverses formes,iespotaplicaraunaàmpliavarietatdesituacions.Unad’aquestes situacionsqueseriainteressantd’analitzar,enrelacióambl’evoluciódelcàncer ilasevateràpia,éslaintroducciódequiescènciainduïdaperlahipòxia.Les cèl.lulescancerígenestenenl’habilitatdetornar-sequiescentssotacondicions d’hipòxia;vegeu[1, 7].Pertant,seriainteressantintroduiraquestacapacitaten elnostremodel,especialment,enelcontextdemodelsdecompetènciaentre cèl lulesquenomanifestenquiescènciainduïdaperhipòxia(cèllulesnormals) icèl.lulesquesíquepassenaserquiescents(cèl.lulescancerígenes)[2];en particular,quanestractadepredirelresultatdeteràpiesespecífiquesdel ciclecel.lular,onlescèl.lulesesmatenquanentrenenfasesdeterminades delciclecel.lular[44].Aquestaanàlisiesposposaperauntreballfutur.

Unproblemarelacionatqueseriainteressantd’explorarusantlametodologiadescritaenaquestapublicacióéselproblemadelmetabolismedeles cèl lulescancerígenes(ésadir,l’efecteWarburg).D’entreelsdiversoscanvis fenotípicsinduïtsperl’efecteWarburg,undelsmésremarcables,juntament ambl’incrementdelataxad’acidificacióextracel.lular,éslareducciódela taxadeconsumd’oxigen(OCR)[13].Seriainteressantd’analitzarl’efectede considerartipusdecèl.lulesdiferentscaracteritzadesperestatsmetabòlics diferents,ésadir,taxesdeconsumd’oxigendiferentsi,mésespecialment, lasevarelacióambelsefectesdelahipòxia.Aquesttemaseràestudiatmés profundamentenunarecercafutura.

Ensproposemtambéestendreelnostrecontextestocàsticmultiescalaper tald’inclouregrausdellibertatenl’espaiil’acoblamentaunmodeld’angiogènesiinduïdapertumors.Pertaldefer-ho,necessitemrecórreramètodesde simulacióestocàsticaméseficients,com,perexemple,elmètodedelareacció següent[19].

AApèndix

Aquestapèndixestàdedicataestablirlarelacióentreelsparàmetresdel nostremodelestocàstic, d1, d 1, d2 d3, d 3, d4,ielsvalorsdelsparàmetres macroscòpics donatsa[1].Pertald’aconseguir-ho,apliqueml’aproximacióde l’estatquasiestacionari(QSSA)al’esquemadereacciósegüent:

X1 + E1 d1 d 1 C1 d2 → E1 + X activaciódeCdh1/APC, X + E2 d3YM d 3YM C2 d4YM → E2 + X1 desactivaciódeCdh1/APC,

onelsparàmetres d1, d 1, d2 d3, d 3, d4 estanrelacionatsambaquellsque apareixena[1]atravésdelaQSSAproposadaperBriggsiHaldane.

Aquestesequacionsdecampmitjàperaaquestmecanismedereaccióestan donadesperunsistemad’EDO,equació (A.1),peralestaxesdecanvidecada

PilarGuerreroiTomásAlarcón

unadelesespèciesinvolucrades:

dx1 da =−d1x1e1 + d 1c1 + d4ymc2,

de1 da =−d1x1e1 + (d 1 + d2)c1, (A.1)

dc1 da = d1x1e1 (d 1 + d2)c1,

dx da =−d3xyme2 + d 3ymc2 + d2c1,

de2 da =−d3xyme2 + (d 3 + d4)ymc2,

dc2 da = d3xyme2 (d 3 + d4)ymc2,

dy da = a4 (a1 + a2x + a3z)y,

on x1 = [X1], x = [X], ci = [Ci] i ei = [Ei].Amés,hemusatleslleisde conservació: dei da + dci da = 0,d’onpodemconclourequelaconcentraciótotal del’enzimésconstant: ci + ei = e0 (i = 1, 2),i dx1 da + dc1 da + dx da + dc2 da = 0,de maneraquelaconcentraciótotaldeCdh1esconserva: x1 + c1 + x + c2 = s0.

Pertaldecontinuar,introduïm,fentuncanvid’escala,lesvariablessegüents:

x1 = x1 s0 , x = x s0 , ci = ci e0 ,(i = 1, 2),τ = d3e0y0a, = e0 s0 , y = y y0 , d’acordamblesqualsobtenimelsistemasegüent:

dx1 dτ =− d1 d3y0 x1(1 c1) + d 1 d3y0s0 c1 + d4 d3s0 ymc2,

dc1 dτ = d1 d3y0 x1(1 c1) (d 1 + d2) d3y0s0 c1,

dx dτ =−xym(1 c2) + d 3 d3s0 ymc2 + d2 d3y0s0 c1,

dc2 dτ = xym(1 c2) (d 3 + d4) d3s0 ymc2

Modelsestocàsticsmultiescaladepoblacionscel.lulars

Ara,preneml’aproximaciódel’estatquasiestacionari, dci dτ = 0(i = 1, 2), queensportaa: c1 = d1x1 d 1+d2 s

= x2

Uncoparribatsaaquestpunt,utilitzemlalleideconservació

1 dτ + dc1 dτ + dx dτ + dc2 dτ = 0,ésadir, x1 + x = 1,demaneraquel’equació (A.2) potserreescrita com:

dτ =− ymx

laqualcosadónallocalarelaciósegüententreelsparàmetresdelnostre modelestocàsticiaquellsqueapareixienal’aproximaciódecampmitjàde lareferència[58]: d2 = (1 + b3u)s0/e0, d4 = b4s0/(y0e0), d 1 = J3s0d1 d2, d 3 = J4s0d3 d4,on bi i Ji (i = 3, 4)són,respectivament,taxesconstants (b3 i b4)ilesconstantsdeMichaelis-Menten(J3 i J4).Aquestaequivalènciaens permetdonarvalorsalsparàmetresdelnostremodelestocàstic,demanera queelcomportamentdecampmitjàéselmateixqueenelsmodelsd’Alarcón etal. a[1]iTysoniNovaka[58].

Agraïments

ElsautorsagraeixenalMinisterideCiènciaiInnovacióespanyol(MICINN)elseu finançament,sotalesbequesMTM2011-29342;alaGeneralitatdeCatalunya,el finançamentsotalabeca2009SGR345,ialaWellcomeTrust(098325).

Referències

[1] Alarcón,T.;Byrne,H.M.;Maini,P.K. «Amathematicalmodelofthe effectsofhypoxiaonthecell-cycleofnormalandcancercells». J.Theoret. Biol.,229(3)(2004),395–411.

[2] Alarcón,T.;Byrne,H.M.;Maini,P.K. «Amultiplescalemodelfortumor growth». MultiscaleModel.Simul.,3(2)(2005),440–475.

[3] Alarcón,T.;Page,K.M. «MathematicalmodelsoftheVEGFreceptorand itsroleoncancertherapy». J.R.Soc.Interface,4(13)(2007),283–304.

[4] Alberts,B.;Bray,D.;Lewis,J.;Raff,M.;Roberts,K.;Walson,J.D. Molecularbiologyofthecell.3aed.NovaYork:GarlandPublishing,1994.

[5] Anderson,A.R.A.;Chaplain,M.A.J. «Continuousanddiscretemathematicalmodelsoftumor-inducedangiogenesis». Bull.Math.Biol.,60(5) (1998),857–899.

[6] Ball,K.;Kurtz,T.G.;Popovic,L.;Rempala,G. «Asymptoticanalysis ofmultiscaleapproximationstoreactionnetworks». Ann.Appl.Probab., 16(4)(2006),1925–1961.

[7] Bedessem,B.;Stéphanou,A. «AmathematicalmodelofHiF-1α-mediated responsetohypoxiaontheG1/Stransition». Math.Biosci.,248(2014), 31–39.

[8] Binney,J.J.;Dowrick,N.J.;Fisher,A.J.;Newman,M.E.J. Thetheoryof criticalphenomena:Anintroductiontotherenormalizationgroup.Oxford: OxfordUniversityPress,1992.

[9] Box,A.H.;Demetrick,D.J. «Cell-cyclekinaseinhibitorexpressionand hypoxia-inducedcell-cyclearrestinhumancelllines». Carcinogenesis, 25(12)(2004),2325–2335.

[10] Breward,C.J.W.;Byrne,H.M.;Lewis,C.E. «Theroleofcell-cellinteractionsinatwo-phasemodelforavasculartumourgrowth». J.Math.Biol., 45(2)(2002),125–152.

[11] Byrne,H.M. «Dissectingcancerthroughmathematics:fromthecelltothe animalmodel». NatureReviewsCancer,10(3)(2010),221–230.

[12] Cao,Y.;Gillespie,D.T.;Petzold,L.R. «Efficientstepsizeselectionfor thetau-leapingsimulationmethod». J.Chem.Phys.,124(2006),044109.

[13] Chen,Y.;Cairns,R.;Papandreou,I.;Koong,A.;Denko,N.C. «Oxygen consumptioncanregulatethegrowthoftumors,anewperspectiveonthe Warburgeffect». PLoSONE,4(9)(2009),e7033.

[14] Deisboeck,T.S.;Wang,Z.;Macklin,P.;Cristini,V. «Multiscalecancer modeling». AnnualReviewofBiomedicalEngineering,13(2011),127–155.

[15] Durrett,R. «Cancermodeling:apersonalperspective». NoticesAmer. Math.Soc.,60(3)(2013),304–309.

[16] Funk,J.O. «Cancercell-cyclecontrol». AnticancerRes.,19(1999),4778–4780.

[17] Gardiner,C. Stochasticmethods.Ahandbookforthenaturalandsocial sciences.4aed.Berlín:Springer-Verlag,2009.(SpringerSeriesinSynergetics)

[18] Gardner,L.B.;Li,Q.;Park,M.S.;Flanagan,W.M.;Semenza,G.L.; Dang,C.V. «HypoxiainhibitsG1/Stransitionthroughregulationofp27expression». J.Biol.Chem.,276(11)(2001),7919–7926.

Modelsestocàsticsmultiescaladepoblacionscel.lulars 163

[19] Gibson,M.A.;Bruck,J. «Efficientexactstochasticsimulationofchemical systemswithmanyspeciesandmanychannels». J.Phys.Chem.A,104(9) (2000),1876–1889.

[20] Gillespie,D.T. «Ageneralmethodfornumericallysimulatingthestochastictimeevolutionofcoupledchemicalreactions». J.ComputationalPhys., 22(4)(1976),403–434.

[21] Gillespie,D.T. «Approximateacceleratedstochasticsimulationofchemicallyreactingsystems». J.Chem.Phys.,115(2001),1716.

[22] Gillespie,D.T.;Petzold,L.R. «Improvedleap-sizeselectionforacceleratedstochasticsimulation». J.Chem.Phys.,119(2003),8229.

[23] Green,S.L.;Freiberg,R.A.;Giaccia,A.J. «p21Cip1 andp27Kip1 regulate cellcyclereentryafterhypoxicstressbutarenotnecessaryforhypoxiainducedarrest». Mol.Cell.Biol.,21(2001),1196–1206.

[24] Grimmett,G.R.;Stirzaker,D.R. Probabilityandrandomprocesses.3aed. NovaYork:OxfordUniversityPress,2001.

[25] Hand,P.E.;Griffith,B.E. «Adaptivemultiscalemodelforsimulatingcardiacconduction». Proc.Natl.Acad.Sci.USA,107(33)(2010),14603–14608.

[26] Hester,S.D.;Belmonte,J.M.;Gens,J.S.;Clendenon,S.G.;Glazier,J.A. «Amulti-cell,multi-scalemodelofvertebratesegmentationandsomite formation». PLoSComput.Biol.,7(10)(2011),e1002155.

[27] Jiang,Y.;Pjesivac-Grbovic,J.;Cantrell,C.;Freyer,J.P. «Amultiscale modelforavasculartumorgrowth». Biophys.J.,89(6)(2005),3884–3894.

[28] Kim,Y.;Othmer,H.G. «Ahybridmodeloftumor-stromalinteractionsin breastcancer». Bull.Math.Biol.,75(8)(2013),1304–1350.

[29] Kitano,H. «Cancerasarobustsystem:implicationsforanticancertherapy». NatureReviewsCancer,4(2004),227–235.

[30] Kubo,R.;Matsuo,K.;Kitahara,K. «Fluctuationandrelaxationofmacrovariables». J.Stat.Phys.,9(1)(1973),51–96.

[31] Land,S.;Niederer,S.A.;Louch,W.E.;Sejersted,O.M.;Smith,N.P. «Integratingmulti-scaledatatocreateavirtualphysiologicalmouseheart». InterfaceFocus,3(2013),20120076.

[32] Lignet,F.;Calvez,V.;Grenier,E.;Ribba,B. «Astructuralmodelof theVEGFsignallingpathway:emergenceofrobustnessandredundancy properties». Math.Biosci.Eng.,10(1)(2013),167–184.

[33] Lowengrub,J.S.;Frieboes,H.B.;Jin,F.;Chuang,Y.-L.;Li,X.;Macklin,P.; Wise,S.M.;Cristini,V. «Nonlinearmodellingofcancer:bridgingthegap betweencellsandtumours». Nonlinearity,23(1)(2010),R1–R91.

[34] Macklin,P.;McDougall,S.;Anderson,A.R.A.;Chaplain,M.A.J.;Cristini,V.;Lowengrub,J. «Multiscalemodellingandnonlinearsimulationof vasculartumourgrowth». J.Math.Biol.,58(4–5)(2009),765–798.

[35] Maier,R.S.;Stein,D.L. «Ascalingtheoryofbifurcationsinthesymmetric weak-noiseescapeproblem». J.Statist.Phys.,83(3–4)(1996),291–357.

[36] McCulloch,A.D. «Systemsbiologyandmulti-scalemodellingofthe heart».A: BiomedicalScience&EngineeringConference,2009.BSEC2009. FirstAnnualORNL.Piscataway,NJ:IEEE,2009,1–3.

[37] McDougall,S.R.;Anderson,A.R.A.;Chaplain,M.A.J. «Mathematical modellingofdynamicadaptivetumour-inducedangiogenesis:clinical implicationsandtherapeutictargetingstrategies». J.Theoret.Biol.,241(3) (2006),564–589.

[38] McDougall,S.R.;Anderson,A.R.A.;Chaplain,M.A.J.;Sherratt,J.A. «Mathematicalmodellingofflowthroughvascularnetworks:implicationsfortumour-inducedangiogenesisandchemotherapystrategies». Bull.Math.Biol.,64(4)(2002),673–702.

[39] Menendez,J.;Jovenc,J.;Cufí,S.;Corominas-Faja,B.;Oliveras-Ferraros,C.;Cuyàs,E.;Martin-Castillo,B.;López-Bonet,E.;Alarcón,T.; Vazquez-Martin,A. «TheWarburgeffectversion2.0:metabolicreprogrammingofcancerstemcells». CellCycle,12(8)(2013),1166–1179.

[40] Oates,A.C.;Gorfinkiel,N.;González-Gaitán,M.;Heisenberg,C.-P. «Quantitativeapproachesindevelopmentalbiology». NatureReviewsGenetics,10(200),517–530.

[41] Osborne,J.M.;Walter,A.;Kershaw,S.K.;Mirams,G.R.;Fletcher,A.G.; Pathmanathan,P.;Gavaghan,D.;Jensen,O.E.;Maini,P.K.;Byrne,H.M. «Ahybridapproachtomulti-scalemodellingofcancer». Philos.Trans.R. Soc.Lond.Ser.AMath.Phys.Eng.Sci.,368(1930)(2010),5013–5028.

[42] Owen,M.R.;Alarcón,T.;Maini,P.K.;Byrne,H.M. «Angiogenesisand vascularremodellinginnormalandcanceroustissues». J.Math.Biol., 58(4–5)(2009),689–721.

[43] Perfahl,H.;Byrne,H.M.;Chen,T.;Estrella,V.;Alarcón,T.;Lapin,A.; Gatenby,R.A.;Gillies,R.J.;Lloyd,M.C.;Maini,P.K.;Reuss,M.; Owen,M.R. «Multiscalemodellingofvasculartumourgrowthin3D: therolesofdomainsizeandboundaryconditions». PLoSONE,6(4)(2011), e14790.

[44] Powathil,G.G.;Adamson,D.J.A.;Chaplain,M.A.J. «Towardspredictingtheresponseofasolidtumourtochemotherapyandradiotherapy treatments:clinicalinsightsfromacomputationalmodel». PLoSComput. Biol.,9(7)(2013),e1003120.

[45] Preziosi,L.;Tosin,A. «Multiphaseandmultiscaletrendsincancermodelling». Math.Model.Nat.Phenom.,4(3)(2009),1–11.

[46] Redner,S. Aguidetofirst-passageprocesses.Cambridge:CambridgeUniversityPress,2001.

[47] Rejniak,K.A.;Anderson,A.R.A. «Hybridmodelsoftumorgrowth». WIREsSyst.Biol.Med.,3(1)(2011),115–125.

Modelsestocàsticsmultiescaladepoblacionscel.lulars 165

[48] Ribba,B.;Colin,T.;Schnell,S. «Amultiscalemathematicalmodelof cancer,anditsuseinanalyzingirradiationtherapies». TheoreticalBiology andMedicalModelling,3(2006),7.

[49] Schnell,S.;Maini,P.K.;Newman,S.A.;Newman,T.J. (ed.). Multi-scale ModelingofDevelopmentalSystems.Oxford:AcademicPress,2008.

[50] Setty,Y. «Multi-scalecomputationalmodelingofdevelopmentalbiology». Bioinformatics,28(15)(2012),2022–2028.

[51] Smith,N.P.;Nickerson,D.P.;Crampin,E.J.;Hunter,P.J. «Multiscale computationalmodellingoftheheart». ActaNumer.,13(2004),371–431.

[52] Stacey,D.W. «CyclinD1servesasacellcycleregulatoryswitchinactively proliferatingcells». CurrentOpinioninCellBiology,15(2)(2003),158–163.

[53] Stéphanou,A.;McDougall,S.R.;Anderson,A.R.A.;Chaplain,M.A.J. «Mathematicalmodellingofflowin2Dand3Dvascularnetworks:applicationstoanti-angiogenicandchemotherapeuticdrugstrategies». Math. Comput.Modelling,41(10)(2005),1137–1156.

[54] Strebhardt,K.;Ullrich,A. «PaulEhrlich’smagicbulletconcept: 100yearsofprogress». NatureReviewsCancer,8(2008),473–480.

[55] Szabo,A.;Merks,R.M.H. «CellularPottsmodelingoftumorgrowth, tumorinvasion,andtumorevolution». Front.Oncol.,3(2013),87.

[56] Tracqui,P. «Biophysicalmodelsoftumourgrowth». Rep.Progr.Phys.,72 (2009),056701.

[57] Travasso,R.D.M.;CorveraPoiré,E.;Castro,M.;Rodríguez-Manzaneque,J.C.;Hernández-Machado,A. «Tumorangiogenesisandvascular patterning:amathematicalmodel». PLoSONE,6(5)(2011),e19989.

[58] Tyson,J.J.;Novak,B. «Regulationoftheeukaryoticcellcycle:molecularantagonism,hysteresis,andirreversibletransitions». J.Theoret.Biol., 210(2)(2001),249–263.

[59] vanDrogen,F.;Sangfelt,O.;Malyukova,A.;Matskova,L.;Yeh,E.; Means,A.R.;Reed,S.I. «UbiquitylationofcyclinErequiresthesequential functionofSCFcomplexescontainingdistincthCdc4isoforms». Molecular Cell.,23(1)(2006),37–48.

[60] VanKampen,N.G. StochasticprocessesinPhysicsandChemistry.Amsterdam:Elsevier,2007.

[61] Visintin,R.;Prinz,S.;Amon,A. «CDC20andCDH1:afamilyofsubstratespecificactivatorsofAPC-dependentproteolysis». Science,278(5337) (1997),460–463.

[62] Walpole,J.;Papin,J.A.;Peirce,S.M. «Multiscalecomputationalmodels ofcomplexbiologicalsystems». AnnualReviewofBiomedicalEngineering, 15(2013),137–154.

[63] Zachariae,W.;Nasmyth,K. «Whoseendisdestruction:celldivisionand theanaphase-promotingcomplex». GenesDev.,13(1999),2039–2058.

PilarGuerrero

DepartmentofMathematics UniversityCollegeLondon GowerStreet LondonWC1E 6BT,UK

i CentredeRecercaMatemàtica CampusdeBellaterra,EdificiC 08193 Bellaterra,Barcelona,Spain pguerrero@ucl.ac.uk

TomásAlarcón

CentredeRecercaMatemàtica CampusdeBellaterra,EdificiC 08193 Bellaterra,Barcelona,Spain i DepartamentdeMatemàtiques UniversitatAtonòmadeBarcelona 08193 Bellaterra,Barcelona,Spain talarcon@crm.cat

ButlletídelaSocietatCatalanadeMatemàtiques Vol.30,núm.1,2015.Pàg.167–191. DOI:10.2436/20.2002.01.62

Unaanàlisimatemàticadelmovimentd’unapilota defutboldurantelvol

TimothyG.MyersiSarahL.Mitchell

Resum: Enaquestarticleespresentaunestudianalíticinumèricdelesequacions tridimensionalsquedescriuenelmovimentd’unapilotaquegiraal’aire.L’anàlisiinicial consideracoeficientsdefregamentconstantsidespréss’esténalcasd’unfregament quedepèndelavelocitatderotaciódelapilota.S’observaunacoincidènciaexcel lent entreelsresultatsnumèrics,elsanalíticsielsexperimentals.Lasolucióanalíticaens mostrademaneraexplícitacomelmovimentdelapilotadepèndeparàmetrescom larugositat,lavelocitatilescondicionsatmosfèriques.Esdemostralaimportància d’aplicarmodelstridimensionalsencomptesd’aproximacionsbidimensionals.

Paraulesclau: aerodinàmica,trajectòriad’unapilotadefutbol,pilotadefutbolgirant, forçadeMagnus,soluciódepertorbació.

ClassificacióMSC2010: 34L30,76G25.

1Introducció

Alllargdelsanyss’haavançatmoltenrelacióambeldissenydelespilotesde futbol,desdelatradicionalpilotadecuirqueenvoltavaunabufetadeporc infladaalamésrecentJabulani,queesconstrueixfentservirpanellsdepoliuretà. L’objectiudelsavençostecnològicseneldissenydelespilotesdefutbolha estatferlapilotamésfiableimillorperaljoc,enbeneficidetotselsjugadors. Recentment,enungrupd’estudidematemàtiquesalaindústriaenunareunió celebradaaJohannesburg,l’entrenadord’unequipdeprimeradivisiósud-africà, elBidvestWits,vaplantejarlapreguntadesiunapilotadefutbolespotescollir demaneraquebeneficiïl’equiplocal(o,alternativament,desafavoreixil’equip visitant).Aquestarticlehasortitd’aquestestudiialesconclusionsesdiscuteix lapreguntadesiespottriarunapilotaque,efectivament,doniunavantagea l’equiplocal.

EnelspartitsdefutbolprofessionalaSud-àfrica,iamoltsaltrespaïsos, l’equiplocaléselqueproporcionalapilotaqueesfaràservirdurantelpartit. L’elecciódelapilotaestàlimitada,principalment,perlallei2delaFIFA,que

AquesttreballfouelguanyadordelpremiAlbertDoudel’any2014ivaaparèixerenanglèsamb eltítol«Amathematicalanalysisofthemotionofanin-flightsoccerball»a SportsEngineering, 16(2013),29–41.AgraïmaSpringerScience+BusinessMediaelpermísperalasevapublicació. LatraduccióalcatalàésdegudaaHelenaRibera.

TimothyG.MyersiSarahL.Mitchell

endictalamida,elpes(ensec),lapressióielmaterial.Peraquestmotiuels principalscanviseneldissenydelapilotas’hanproduïtenelmaterialien laformadelspanells[13].Unaaltralimitacióvedonadapelpatrocinador,ja quel’equiphad’usarunadelessevespilotes.EnelcasdelBidvestWitsles pilotessónproporcionadesperNike.DurantlareunióaJohannesburgesvan presentartrespilotesNike,d’aspectemoltsimilar,peròhihaviaunadiferència important:duesdelespiloteserenrugoses(ambpanellsambclots)mentreque latercercateniaelspanellsllisos(vegeu,perexemple,fotosdepropdelaNike T90TracerandCatalystalaweb Nike.com).

Perrespondrealapreguntasobrel’elecciódelapilotal’anàlisiquepresentem acontinuaciósecentraràenelseumovimentatravésdel’airei,enparticular, desd’unafaltaouncórner.Undelsmotiusdetriaraquestscasosésquesón situacionsrelativamentcontroladesihihamoltainformacióenelmovimentde lapilotaatravésdel’aire.Unaltremotiuésqueelsxutsdefaltasónunfactor importantal’horademarcar:alaCopadelMóndel1998,42dels171gols marcatsvanvenirdejugadesassajadesiun50%erenxutsdefalta[2].En conseqüència,entendreelmovimentdelapilotadesd’unxutdefaltaod’un córnerpodriaaportarinformacióimportantal’horad’escollirlapilota.L’últim motiuésqueJohannesburgestàsituadaaunnivellsobreelmarmoltalt(més omenysa1800 m).Ladensitatdel’aireésaproximadamentun20%mésbaixa quealnivelldelmar[10]aixíquecalesperarqueladiferènciamésgranenel movimentdelapilotaentreJohannesburgiciutatssituadesaunaaltitudmés baixasiguiquanaquestmovimentesprodueixal’aire.

Perdescomptatquehihahagutmoltstreballssobreelmovimentdeles pilotesielsprojectilsal’aire.Apartirde1600Newtonvaobservarqueuna pilotadetennisambefecteteniaunatrajectòriacorbada.Unsegleméstard Robinvamostrarqueenunaesferagiratòriahihaviaunaforçaaerodinàmica transversal:aixòéselquearas’anomena l’efecteMagnus (odemaneramésjusta l’efecteRobin-Magnus).Capafinalsdels1800,Taitvaserelprimeraaplicar aquestconcepteaunapilotarelacionadaambl’esport(desafortunadamentuna pilotadegolfenllocd’unapilotadefutbol).Totsaqueststreballserensobre fluidssensefriccióaixíqueperl’explicaciócorrectadel’efecteMagnusesva haverd’esperarfinsalateoriadelacapalímitdePrandtlel1904.L’anàlisi específicadelmovimentd’unapilotadefutboldurantelvolvaarribarmolt méstard.Asai etal. [1]vanduratermeunestudiexperimentaldelscoeficients desustentacióenunapilotadefutbolambefecteisenseefecteivanmostrar unafortadependènciadelcoeficientdesustentaciórespectedelavelocitat derotació.Lesequacionsdemovimentd’unapilotadefutbolespodentrobar enmoltstreballsperòenelnostreestudifaremservirlaconvenciódeGoffi Carré[7]enlaquall’efecteMagnusesdivideixenunacomponentd’ascensió ienunacomponentlateral(Asai etal. tambéutilitzenduescomponents). Hörzer etal. [10]proporcionendetallsútilsdelesdiferènciesenlescondicions atmosfèriquesentrediversesseusdelaCopadelMónaSud-àfricaidemostren l’efectedel’altitudenlatrajectòria.OggianoiSætran[11]comparenlatrajectòria depilotesdefutboldiferents:aixòconfirmalacreençaquel’elecciódelapilota potconstituirunavantatgeperal’equipdecasa.

Aquestarticles’organitzadelamanerasegüent.Alasecció2esdónaelmodel matemàtictridimensional,queésbenconegutiqueesbasaessencialmentenla segonalleideNewton.Acausadelano-linealitatdelesequacionsdelmoviment toteslessolucionspublicadesambanterioritats’hanobtingutnumèricament. Enunaanàlisid’unmodelméssimplequeelconsideratenl’estudipresent, BrayiKerwin[2]afirmenquelesequacionsqueregeixenelmovimentno tenensolucióenformatancada,iencaraqueaixòéstècnicamentcorrecte,ala secció3esdedueixunasolucióaproximadaexacta.D’aquestamaneraesmostra claramentl’efectedelsparàmetresdelmodelenelmovimentdelapilota,la qualcosanoéspossibleambunasoluciónumèrica.Alasecció4escalculen solucionsnumèriquesperverificarl’exactituddelasolucióaproximada.Estudis experimentalssobrecoeficientsdefregamentid’elevacióhandemostratlaseva dependènciadelarotació,peròelsestudisteòricsgeneralmentdeixenaquests coeficientscomaconstants.Alasecció5s’esténl’anàlisifetapertaldetractar elcasdecoeficientsvariables.Finalment,esdiscuteixlaqüestiódesil’elecció delapilotarealmentpotdonarunavantatgeal’equipdecasa.

2Modelmatemàtic

Elmovimentd’unapilotadefutbolestàdescritperlasegonalleideNewton, F = mx,onlaforça F escompondelagravetatidelfregamentambl’aire. Peraunapilotaquenogira,elfregamentnomésactuaenelsentitoposatal movimentdelapilota.Peraunapilotaquegiraelfregamenttéduescomponents, laresistènciaencontradelmovimentendavantilaforçadeMagnus.Laforça deMagnusactuaenladireccióperpendicularaladirecciódelmovimentia l’eixderotació.Aquestaforçaespotsepararenduescomponentsquedenoten movimentd’elevacióimovimentlateral;vegeu[1, 7].Silapilotaesmouenla direcciódefinidaperlavelocitatdelvector ˆ v (onelbarretindicaelvectorunitat), aleshoresespotdefinirunsegonvector ˆ l,queésperpendiculara ˆ v peròque romanenelmateixplaque ˆ v ielvectorgravetat, ˆ g.Notemquelacomponent z de ˆ l éspositiva(i.e. apuntaamunt).Unsistemaorientatpositivamentesdefineix atravésd’untercervector ˆ l × ˆ v.Elsistemadecoordenadesielsvectorses mostrenalafigura1.D’aquestamanera,laforçadefregamentques’oposaal moviment, Fd,actuaenladirecció ˆ v,l’aixecament Fl actuaenladirecció ˆ l ila forçalateral Fs actuaenladirecció ˆ l × ˆ v.Laforçatotalesdefineixcom

F = mg + Fd + Fl + Fs (1)

Pertaldesepararlescomponentsdelgirs’handedefinirduesvelocitats derotació: ωl éslavelocitatalvoltantdel’eix ˆ l i ωs éslavelocitatalvoltant del’eix ˆ l × ˆ v.Sinoméss’utilitzauneixderotació(perexemplecomesdefineix a[10]),elqualestàcontingutenelpla ˆ l, ˆ l × ˆ v,llavorsl’eixfaunangle Ω amb l’eix ˆ l × ˆ v,on tan Ω = ωl/ωs .Noteuqueelproblemaplantejataquíésmés generalquel’estudiata[2],onl’eixderotacióestàcontingutsolamentenel pla x-z

TimothyG.MyersiSarahL.Mitchell

Figura1: Sistemadecoordenades.

Elssignesdelesforcesdepenendequinaconvenciós’utilitzi.Laforçade fregament Fd ésobviqueactuaendireccióoposadaalmovimentdelapilota. Siesconsideraungirlateralpur,aleshoresl’eix z ésl’eixderotació.Utilitzant notacióestàndardperacoordenadespolars,comesmostraenlafigura1,amb ψ contingutenelpla x-y imesuratdesdel’eix x,idefinint ψ = ωs ,aleshores laforçaresultant Fs actuaenladirecciónegativade x.Sinoméshiharotació endavant,llavorsl’eixderotacióés x ialeshores θ = ωl ilaforçaresultant Fl actuaenladirecciónegativade z.Pertant,sóncerteslesrelacionssegüents:

Aquí m éslamassadelapilota, A éslasevaàreatransversal, ρ ésladensitat del’aire, Ci sónelscoeficientsdefregamenti

v|= (x2 + y 2 + z2), (3) on v = (x,y,z) éselvectorvelocitat.Elproducte ˆ l × ˆ v actuaenladirecció negativade x,demaneraquenohihasignenegatiuenl’expressióde Fs .Els coeficientsdefregament Ci varienamb Re = ρ|v|D/µ (on D éseldiàmetredela pilotai µ laviscositatdel’aire)ielparàmetrederotació Sp = Dω/(2|v|) [1, 5]. Lavariacióde Cd respectede Re mostrauncanviradicalquanlapilotaesmou atravésdelatransiciólaminar-turbulenta.Elsresultatsexperimentalsdela posttransicióde[1]indiquenque Cd i Cl varienamb Sp peròtenenpocavariació respectede Re;vegeutambé[7].Noteuque,comque Cl i Cs apareixenacausa delmateixefecte,tenenelmateixcomportament.ComquelaforçadeMagnus esdescomponenduescomponentshihaduesvelocitatsangulars, ωl i ωs Aleshoreslavariacióde Cl i Cs respectede Sp significaqueprenendiferents valorssi ωl = ωs .L’avantatged’utilitzardoscoeficientsdefregamentésque elsdiferentseixosderotacióespodendiferenciarfàcilment.Enparticular,per algirlateralpurés ωl = Cl = 0iperalgirendavantpurés ωs = Cs = 0(la relacióentre ω i C esdiscutiràambmésdetallmésendavant).

Elsvectorsunitatespodendefinirentermesdelsdosangles ψ, θ ambles relacionssegüents:

Demaneraalternativaelsanglesentermesdelescomponentsdelavelocitat cartesianaespodenexpressarcoma

on vp = (x,y) éslaprojeccióde v sobreelpla x-y (vegeufigura1).

L’equaciódelmovimentespotescriurearaentermesdelescomponents

Elscoeficientsescalatsdelfregamentsón ki = ρACi/(2m).Estractad’un conjuntd’equacionsdiferencialsordinàriesnolinealsdesegonordresense solucióanalítica.Espodenresoldrefàcilmentdeformanumèricaiespotfer algunavençanalíticdesprésdeferalgunessuposicionsraonablesenrelació ambelmovimentdelapilota:

1.Elseixosespodentriardemaneraquehomxutalapilotaprincipalment enunadirecció(totiquepelviratgeòbviamentesdesviarà).Pertant, suposaremquelapilotaésimpulsadaprincipalmentenladirecció y

2. Elviratgedominantésenladirecciólateral,ésadir,lapilotaesxuta sobretotambefectelateral.

Laprimerasuposicióestradueixenelfetquelavelocitatenladirecció y hade sersignificativamentmésgranquelavelocitatenlesdireccions x i z, y x,z itambéquelapilotaarribamésllunyenladirecció y.Lasegonahipòtesiés certaengeneralenelmovimentd’unapilotadefutbol,jaquenormalment l’efectelateralésmésgranquel’efecteendavant;encanvienunapilotadegolf homesperariaelcontrari.L’anàlisiespotadaptarfàcilmental’efecteendavant peròcomqueaquíenscentremenpilotesdefutbol,l’efectedominantque suposaremésellateral.

TimothyG.MyersiSarahL.Mitchell

3Soluciódepertorbació

Pertaldeprogressaranalíticamentadimensionaremelsistemafentelcanvide variables

X = x L1 ,Y = y L2 ,Z = z L3 ,T = t τ , (11)

on L2 ésladistànciaenladirecció y alaporteria, τ = L2/v ésl’escaladel tempsquelapilotatardaaarribaral’objectiuon v éslavelocitatinicial delapilotaenladirecció y i L3 = gτ 2 ésl’escaladedistànciavertical.Les lletresmajúscules X, Y , T denotenlesvariablesnodimensionals.L’escalade distància L1 és,demoment,desconegudaperòobservemqueacausadela suposició1, L1 L2.

Enprimerlloc,consideremelsvectorsvelocitatielsescrivimentermesde lesquantitatsadimensionals

|v|= L2 τ Y 1+ L2 1 L2 2 X2 Y 2 + L2

on r1, r2 denotenlesarrelsquadrades.Hemaïllatelfactor L2Y/τ jaqueésel termemésgranenl’expressiódelavelocitatialeshores r1,r2 =O(1) (ésadir, lasevamagnitudésdel’ordredelaunitat).

kd 0.013 kl 0.004

ks 0.0108 m 0.45 kg

ρ 1 kgm 3 D 0.22 m

A 0.039 m2 v 25 m/s

Cd 0.3

Cs 0.25

Cl 0.1 L2 20 m

Taula1: Valorstípicsdelsparàmetres;vegeu[1,4,12].

Arapodemescriurelesequacionsqueregeixenelmovimentcoma

Perdeterminar L1 observemqueelmovimentenladirecció x ésproduïtjasigui perunavelocitatinicialjasiguiperlacomponentderotacióenladirecció y. Comquel’estudisecentraenelviratgecausatpelgir,lavelocitatinicialen

Matemàtiquesdelmovimentd’unapilotadefutbol 173

ladirecció x észero, x(0) = ˙ X(0) = 0.Eltermedominantal’equació (13) és eltermequeporta Y 2 jaqueelsvectorsvelocitatestanescalatsdemanera que r1,r2 =O(1), L1 = ks L2 2.Utilitzantelsvalorsdelsparàmetresdelataula1 resultaque L1 ≈ 4 m,ésadir,homesperaquelapilotaviatgidel’ordre de4 m lateralmentdurantelseuvol.Eltermedominantenl’equació (14) és tambéelqueporta ˙ Y 2.Tenim kd = 0.013, kdL2 = 0.26iaixòhoexpressem amb ε = kdL2,queésunparàmetrepetit(i ε2 ≈ 0.07).Elstermesqueporten l’arrelquadrada r1, r2 contenenlesràtios L2 1/L2 2 ≈ 0 04, L2 3/L2 2 ≈ 0 25,que denotemper c1ε2 i c2ε,respectivament(noteuque ks L1 = L2 1/L2 2).Finalment, klL3 ≈ 0 03 = c3ε

Aralesequacionssón

(16)

(19)

Notemquelahipòtesiquehomxutalapilotasobretotambefectelateralvoldir queelstermes kl apareixenalesequacionsde X, Y ambunordremésbaixque elstermes ks (atravésdelcoeficient c3).Enl’equacióde Z l’enlairamentésla forçadominantdesprésdelagravetat,pertanthiapareixambunordre O(ε). Quanlarotacióendavantdomina,l’escalats’hadecanviardemaneraconvenient.

Uncopescriteslesequacionsenformaadimensionalpodemferalgunes observacionssobreelcomportamentdelasolució,senseresoldreelsistema. Perexemple,totselstermesde (17) tenenelparàmetrepetit ε,queindica queelmovimentdominantenladirecció Y estàdescritperl’equació Y = 0i queelfregament,representatper ε,téunefecterelativamentpetit.Comque ε = 0.26,obviarelstermesamb ε podriaportaraunerrordelvoltantdel26%. Elmovimentenladirecció Z estàdominatperlagravetat.Elmovimentenla direcció X estàdominatperlacontribucióde ˙ Y (reflectintelfetquelaforça deMagnusésdegudaaladiferènciaentrelavelocitatequatorialilavelocitat endavant,queésaproximadament ˙ Y ).Totiaixò,elmésinteressantésque,com que r1 contéelterme ε(Z/Y)2,lavelocitatenladirecció Z contribueixatotes lesequacions.Ésmés,afectal’equacióde X enunordre ε, i.e. peralsparàmetres queusemara,notenirencompteelmovimentenladirecció Z potportara errorsdelvoltantdel26%.Òbviamentaixòpottenirconseqüènciessignificatives peraqualsevolexperimentons’utilitziunaanàlisidosdimensionalpermodelar elmovimenttridimensionaldelapilota.Aquestfetesdiscuteixambmésdetall alasecció4,deresultats.

TimothyG.MyersiSarahL.Mitchell

Lescondicionsinicialssónqueelmovimentdelapilotacomençaal’origen isurtambunavelocitat(dimensional) (0,v,w).Noteuquelavelocitaten ladirecció x sempreespotsuposarnul la,simplementdefinintl’eix y comla direcciódelxutenelpla x-y.Enformaadimensionalaquestescondicionssón

X(0) = Y(0) = Z(0) = 0, X(0) = 0, Y(0) = 1, Z(0) = W ,on W = wτ/L3

Pertaldedeterminarunasoluciódepertorbacióestàndardbasadaenel paràmetrepetit ε escrivim

Lasoluciófinsal’ordre O(ε2) és

BrayiKerwin[3]estudienunsistemasimplificatdosdimensional.L’anàlisi quefanesbasaaigualarl’acceleracióaltermemésgrandelsmembresdela dretadelesequacions.Apartirdelesequacions (16) i (17) aixòredueixel problemaa

(24) oncalremarcarque

(25)

Perrelacionaraquestessolucionsamblesdelesequacions (21) i (22) utilitzem eldesenvolupamentdeTaylorpera ε 1itrobem

(27)

Matemàtiquesdelmovimentd’unapilotadefutbol 175

Sifixem W = ci = 0a (21) i (22),pertald’eliminarladependènciaen Z iferquela soluciósiguibidimensional,llavorslessolucionsde x difereixenenl’ordre O(ε), mentrequelessolucionsde y difereixenenl’ordre O(ε2).Lasimplificacióde tenirencomptenoméselstermesmésgransdelsmembresdeladretadeles equacionspermetposardemanifestcorrectamentelcomportamentdominant, peròenelcasdelviratgelateralpotportaraerrorsentotselstermesposteriors. Pertant,aquestaformadesoluciódonaràunaaproximacióraonableenel resultatnumèricpera y peròunademoltméspobrapera x il’erroraugmenta amb ε (perexemple,siincrementemelvalorde L2).Encaraensdesviemmésde lasoluciócorrectapelfetdenotenirencompteeltermedelmovimenten Z Discutiremaixòmésendavantenelcontextdelessolucionsmostradesala secció4.

Tornemaraalesvariablesdimensionals X = x/L1, Y = y/L2, Z = z/L3, T = t/τ,on L1 =

v sónladistànciaila velocitatinicialsenladirecció y.Lesconstantss’hand’expressarentermes delsparàmetresdimensionals

Lasoluciódimensionalés

Noteuque,atèsquelesexpressionssónmésaviatcomplicades,nomésles escrivimfinsal’ordre O(ε) (elstermes O(ε) estanentreclaus).Enaquestes expressionspodemveureclaramentl’efectequetécadaparàmetre.L’equació pera y ensmostraqueladistànciarecorregudaésaproximadamentproporcionalalavelocitatinicialialtemps,peròqueelfregamentlaredueixique l’acciódelfregamentaugmentaambeltemps.Enladirecció z ladistància recorregudavedeterminadaprincipalmentperlavelocitatinicialilagravetat, peròl’acciótantdelfregamentcomdel’aixecamenttendeixenacanviar-ho. Altrecop,aquestesconseqüènciesaugmentenambeltemps.Detotesmaneres, comqueelviratgedegutal’efectelateralésl’objecteprincipald’aquestestudi, l’equaciópera x éslamésrellevant.Enaquestaequacióveiemque,finsal’ordre principal,ladistànciarecorregudaenladirecció x ésproporcionalalcoeficient defregamentlateral ks itambéa (vt)2.Eldissenydelapilotailescondicions atmosfèriquescontribueixenatravésde ks i,pertant,eldissenydelapilotaés moltimportantpelquefaalviratge.Elproducte vt éslaprimeraaproximació

TimothyG.MyersiSarahL.Mitchell

aladistànciarecorregudaenladirecció y.Ladependènciaquadràticaindicala importànciadexutarllunydelaporteria.Commésviatgilapilota,mésvirarà (aixòésbenconegutentreelsespecialistesdexutslliuresquesempreintenten mourelapilotallunydelaporteria).Potserl’exemplemésfamóséslafalta llençadaperRobertoCarloscontraFrançael1997,quevaproduirunacorba espectacularalfinaldelvoldelapilota.Aquestxutesvaferaproximadamenta 35 m delaporteria;vegeu-loaYouTubeo[6].Elfregamentfrontal kd intervé alprimerordreiactuareduintelviratge.Unacaracterísticaimportantdela solucióésqueelmovimentvertical,atravésde g ide w,tambéintervéalprimer ordre.Laformaquadràtica g2t2 4gwt + 6w 2 éspositivasempreque w ≥ 0 (i.e. lapilotanoesxutacontraterra)itambéactuaperaincrementarelviratge. Unaanàlisibidimensionalnopodràcaptaraquestefecteilacomparacióamb lesdadesexperimentalsportaràaunasobreprediccióde ks .

Acausadelesdiferènciespelquefaaladependènciarespectedeltemps delstermesdelesequacions (29)–(31),aqueststermesseranmenysprecisosa mesuraqueeltempsaugmenti.Aquestfenomenésl’anomenat efectesecular Elcol.lapseesproduiràquanelstermesd’ordre O(ε) passinaserd’ordre O(1). Enelcasdel’equaciópera x aixòpassaquan t ∼ 1/(kdv) ≈ 3 s.Lesequacions pera y i z indiquentempsd’uns9 s.Jaqueelvold’unapilotadefutbolés típicamentd’unsegon,aquestesaproximacionsserveixenperaxutsraonables inocalconsiderarl’efectesecular.

4Resultatsnumèricsianalítics

Figura2: (a)al’esquerra,soluciónumèricaquemostraunatrajectòria dimensionald’unapilotadefutbolquehaestatxutadaal’angledela porteria;(b)aladreta,representacionsde x i z enfuncióde y

Lasoluciónumèricadelesequacions (16)–(18) s’hacalculatutilitzantla rutinaODE45de MATLAB.Alafigura2(a)esmostraunatrajectòriatridimensional d’unapilotaxutadaambcondicionsinicials v = 25 m/s, w = 8 76 m/s,iauna

distànciade L2 = 20 m del’objectiu.L’eleccióde w esvaferdemaneraquela pilotaacabésapropdeltravesserdelaporteria(comqueseguimelcentrede massadelapilota,l’alçadadelaporteriaesprende2 34 m,ésadir,l’alçada estàndardd’unaporteriamenyselradidelapilota).Elsaltresparàmetreses podentrobaralataula1.Perrecórrer20 m enladirecció y estarden0 9112 s (sensefregament, t = 20/25 = 0.8 s).Lafigura2(b)mostralavariacióde x i z enfuncióde y.Delacorbade x espotdeduirquelapilotaviatjauns2.3 m, ambunavariacióaproximadamentquadràtica.Enladirecció z l’alturadela pilotaaugmentafinsqueésapropdelaporteria,iaconsegueixunmàximde 0 4 m persobredelaporteria.Permostrarlatrajectòriad’unamaneraclara, lafigura2utilitzaquantitatsdimensionals.Quansiguipossible,enlesfigures següents,preferiremutilitzarquantitatsadimensionalsjaquefanmésclares lesdiferènciesenelmoviment.Tambépermetencombinarresultats,comala figura2,onlessolucionsde x ide y estandibuixadesalamateixagràfica.

Figura3: Trajectòriesadimensionalsde X, Y i Z enfuncióde T :solució numèricacompleta(líniacontínua),solució O(ε0) (líniadepunts),solució O(ε) (líniadepuntsiratlles)isolució O(ε2) (líniadiscontínua).Els valorsdelsparàmetressón Cd = 0.3, Cs = 0.25i Cl = 0.1.

Alafigura3mostremlavariacióde X, Y i Z enfuncióde T ,perales mateixescondicionsquealafigura2,peròenaquestcass’inclouenlesdiverses solucionsdepertorbació.Enunitatsadimensionalseltempsdevolés T = 0 9112 × 25/20 ≈ 1 14.Lalíniacontínuacorresponalasoluciónumèrica,la líniadepuntscorresponalapertorbaciód’ordreprincipal,lalíniadepunts iratllescorresponalprimerordreilalíniadiscontínuacorresponalsegon ordre.Encadacasl’ordreprincipaldónaunaaproximacióraonableperatemps petitsperòperdexactitudràpidament.Perdescriureelvolsencer,lasolució depertorbaciópera Y ésprouexactafinsalprimerordre,peròperales solucionsde X i Z ésmenysexacta.Toteslescorbesmostrenunacoincidència excel lental’ordre O(ε2).Comquelasoluciódesegonordreimplicaobviar

TimothyG.MyersiSarahL.Mitchell

termesd’ordre O(ε3) ≈ 0 02,espodenproduirerrorsdel’ordredel2%.De fet,l’erroraugmentaambeltempsiésclarquevalzeropera T = 0acausa delaimposiciódelacondicióinicial.Enladirecció X elmàximerrorentrela soluciónumèricailadesegonordreésdequasiel3%iaixòpassaalfinaldel vol.Aquestfetestàd’acordambladiscussióprèviasegonslaquallessolucions aproximadescomencenacol lapsar-seamesuraqueeltempsavança.Noteu quelamateixaconclusióserveixperalproblemadimensional.

Figura4: Comparaciódelasoluciónumèrica(líniacontínua)ilasoluciódepertorbaciódesegonordre(líniadiscontínua)pera X:(a)amb movimentvertical;(b)negligintelmovimentvertical.

Alaseccióanteriors’hadiscutitelproblemaaparentdenegligirelmovimentverticali,enparticular,s’havistqueaquestproblemaseriamésevident enelmovimentenladirecció X.Recuperemaraunmodelbidimensional, ambmovimentnomésenelpla X-Y ,atravésdelasolucióobtingudaposant c2 = c3 = W = 0alesequacions (21) i (22).Alafigura4escomparalasolució numèrica(líniacontínua)ilasoluciódepertorbació(líniadiscontínua)pera X finsalsegonordre.Lesduescorbesetiquetadesamb(a)inclouenelmoviment enladirecció Z ilesetiquetadesamb(b)ignorenaquestmovimenten Z.Si obviemelmovimenten Z elviratgedecreixentornd’un4.5%.Aquesterror s’incrementademaneranolinealamesuraque w augmenta:sidoblem w l’erroraugmentaenun30%.Aquestaobservaciótéconseqüènciesòbviesenla interpretaciódelsestudisexperimentals.Perexemple,sicomparemelmodel dos-dimensionalde[3]ambelsexperimentsrealitzatsil’utilitzempercalcular coeficientsdefregament,aleshorespercompensarelfetdenegligirelmoviment enladirecció Z elmodelprediràvalorsmésgransqueelsreals.A[2]sesimplifica elmodelmatemàticsuposantquel’eixderotacióromanenelpla X-Z iper tantelterme ˙ Z del’equació (16) espotnegligir,totiqueesmantéenl’equació de Y .Aquestaaproximaciósemblainconsistentitambéafectaràlapredicció delscoeficientsdefregament.Ésimportantaleshoresimplementarunmodel completamenttridimensionalquanvulguemcalcularparàmetresexperimentals.

Unestudibidimensionaléspossibleperò,atèsquenopodemevitarlagravetat, aquesthauriad’estarconfinatenelpla Y -Z iutilitzarnoméselgirendavant.

4.1Comparacióambdadesexperimentals

Al’articledeCarré etal. [4]espresentenunseguitderesultatsperalmoviment d’unapilotaambefecteosenseefecte.Lesfigures4a,4bi4cde[4]mostren unatrajectòriatípicaperaunapilotaxutadasenseefecte ambunangleinicial d’uns15◦ respectedeterra iambunavelocitatdexutenelventallde17–31 m/s Extreureinformaciód’aquestesfiguresésunproblemasenzilld’ajustdecorbes (enaquestcasesvautilitzarlafunciópolyfitdel MATLAB,queajustalesdades fentservirelcriteridelsmínimsquadrats).Unajustquadràticalesdades y(t) delestrajectòriesdelafigura4bde[4]dóna

y ≈ a0 + a1t + a2t2 , (32)

amb a0 =−0.1785, a1 = 17.591, a2 =−1.237.Unajustcúbicalesdades z(t) delafigura4cde[4]dóna

z ≈ b0 + b1t + b2t2 + b3t3 , (33)

amb b0 = 0.0253, b1 = 6.287, b2 =−6.294, b3 = 0.201.Elspuntsdedadeses mostrenalafigura5ambasteriscs.Finalment,lafigura4ade[4]indicaque z(y) ésdelaforma

z ≈ c0 + c1y + c2y 2 + c3y 3 , (34)

amb c0 = 0.008, c1 = 0.371, c2 =−0.023, c3 = 0.0001.

t(s)

Figura5: Comparaciódelesdadesexperimentalsde[4](asteriscs)iles corbesd’ajust(líniescontínues).

TimothyG.MyersiSarahL.Mitchell

Apartird’aquestesrelacionsésunproblemasenzilldeterminarunsquants delsparàmetresdelvoldelapilota.Perexemple,l’angleinicialdexut, θ,el podemdeterminarobservantque tan θ = z(0) ˙ y(0) = b1 a1

(35)

Demaneraalternativa tan θ = dz/dy y=0 = c1 ≈ 0.371.Aquestsdosresultats ensdiuenquel’angleinicialdelxutés θ ≈ 19 65o20 35,ambunamitjana aproximadade20◦ (unamicamésaltaquelacitadaenl’article).Lavelocitat inicialenlesdireccions y, z és (y(0),z(0)) = (a1,b1) = (17 591, 6 287) i d’aquestamaneralavelocitatinicial |v|= a2 1 + b2 1 ≈ 18 68 m/s,queforma partdelrangesmentat.

Lacomparacióentreelsajustsdelescorbes (32) i (33) ilessolucionsde pertorbacióde (30) i (31) enspermetobtenirinformacióaddicionalsobreel xut.Enprimerlloc,podemobservarquetant y com z hauriendecomençara l’origen,queéselcasperalasoluciódepertorbació,peròl’ajustdelescorbes indicaunpetiterror.Totiaixò,elstermesrellevants b0, c0 sónpetits.Elsvalors de (v,w) s’obtenenprenent (y(0),z(0)) alesequacions (30) i (31) i,òbviament, (v,w) = (a1,b1).Elcoeficientdefregament kd espotobtenircomparantels termesquadràticsalesexpressionsde y kdv 2 2 = a2 ⇒ kd = 0 008 (36)

quetéunordredemagnitudsimilaralcitatalataula1.Lesexpressionsde z ens donenl’einapercomprovaraquestvalor;comparantelstermescúbicss’obté kdgv 6 = b3 ⇒ kd = 0.007, (37) que,permetenterrorsexperimentalsierrorsenl’ajustdecorbes,estàd’acord amblaprimeraestimació.A[4]s’afirmaqueaquestatrajectòriaéstípicadels casossenseefecte,i,pertant, kl = 0.Hihaunaterceramaneradedeterminar kd: comparanttermesquadràticsenlesexpressionsde z.Aixòensportaaunvalor de kd ≈ 0.025,unresultatquenocoincideixambelstrobatsanteriorment.De totesmaneres,deixant kl = 0,elstermesquadràticsespodenutilitzarper determinar kl = 0.0061quan kd = 0.008,i kl = 0.0065quan kd = 0.007.

Alafigura5,partsuperior,escomparenlesdadesexperimentalsambla funcióquadràticadel’equació (32) peralsvalorscitatsde ai.Aixòésequivalenta dibuixarlasolucióaproximada (30) amb v = 17.591 m/s, kd = 0.008.Clarament lacoincidènciaésmoltbona.Alafigura5,partinferior,escomparenlesdades experimentalsamblafunciócúbicadonadaperl’equació (33) peralsvalors citatsde bi.Aixòésequivalentarepresentarlasolució (31) amb w = 6 287 m/s i kd = 0.007.Unaaltravegada,laconcordançaésexcel lent.

Enresum,lesfuncionssuggeridesperlessolucionsdepertorbaciópoden donarunaconcordançaexcel lentamblesdadesexperimentals.Compararels

coeficientsdelacorbaajustadaamblessolucionsdepertorbacióenspermet calcularelscoeficientsdefregament(itambéespotutilitzarperdeterminarles velocitatsinicialssisóndesconegudes).Comaexemple,s’hanfetservirlesdades donadesa[4]perdeterminarelsparàmetresdelvoldelapilota,queindiquen unangleiniciald’uns20◦ (encontradelsmencionats15◦),uncoeficientde fregament kd ∈ [0.007, 0.008] iuncoeficientd’alçament kl ∈ [0.0061, 0.0065]. Ésparticularmentinteressantelfetdel’apariciód’uncoeficientd’enlairament diferentdezeroenelcasd’unexperimentaparentmentsenseefecte.Atèsque lesequacionsensdonentresmaneresdecalcular kd enabsènciaderotació iquedosd’aquestscaminss’assemblenforça,semblaqueelproblemanoes trobaenlesequacions.Enconseqüènciapodemdeduirquelesgràfiqueshan estatmalpresentades(defet,nomésesdonencomunasolució«típica»),obé ques’hageneratunapetitarotaciódurantelvol,potseracausadelaposició inicialdelacosturaodelavàlvula.

5Coeficientsdefregament

Finsaral’anàlisihatractatambcoeficientsdefregamentconstants.Tanmateix, elsestudisexperimentalshanmostratque Cd, Cl i Cs varienambelcoeficientde rotació Sp = Rω/|v| i,d’algunamanera(silafluctuaciódel’aireésturbulenta), ambelnúmerodeReynolds.Durantelvold’unapilotalavelocitatangular disminueixapocapoc[10].Aixòespotobservarenelsresultatsexperimentals de[9]illavorslavelocitatangularespotprendrecomaconstant,peròla magnitudde |v| disminueixpelfregamenti,pertant, Sp augmenta.

Existeixungrannombred’estudisexperimentalsquemostrenlavariació de Cs (ode Cl)amb Sp;vegeu,perexemple,[1, 5, 9, 11].GoffiCarré[7] resumeixenelsresultatsexperimentalsdeAsai etal. [1]iCarré etal. [5].Observen que,comque Cl i Cs sorgeixendelmateixprocés,sónequivalents(algunsautors noseparenelcoeficientd’enlairamentencomponentsiprefereixentreballar ambundesoldefinitenuneixapropiatderotació;vegeu,perexemple,[10]). Elsresultatsexperimentalsindiquenque Cs i Cl augmentenamblarotaciófinsa estabilitzar-sealvoltantde Sp = 0.3.Elsvalorsrealsvarienambelsexperiments i,comesmostraa[11],ambdiferentstipusdepilota,peròtípicamentvarien entre0i0.35quan Sp augmentade0a0.3[1, 4, 9, 12].Comqueenaquest estudienscentremenl’efectedelgir,enelscàlculsdespreciemlaregióon Sp ésmoltpetit(persotade0 1)iutilitzemunaaproximacióatrossosdelaforma

s =

,Sp> 0.3, (38) onelgradient ms = 0.8, Cs0 = 0.25éselcoeficientquan Sp = Sp0 = 0.15/0.8i Csm = 0.34éselvalorconstantmàximde Cs .Elcoeficientdefregament ks = ks0 s’escriucoma

s0 = ρACs0 2m

TimothyG.MyersiSarahL.Mitchell

Laformalineal,senseeltruncament,tambéhaviaestatutilitzadaperHörzer etal. [10].Elcoeficientdefregament Cd mostraunadependènciamenorrespecte de Sp i,pertant,comaprimerintentpermodelarelscoeficientsvariables permetemque Cs variïmentrequedeixemconstant Cd.

Acausadel’equivalènciade Cs amb Cl,nomésestudieml’efectedevariar unad’aquestesquantitats.Aixòésencertat,jaque,comhemcomentatala seccióanterior,l’anàlisihauriadesertridimensional(llevatquelalimitéssim alpla y-z iimposéssimnomésgirendavant).Sipermetemquetant Cs com Cl variïn,aleshoreslapertorbacióseràextremamentcomplicadadetractar.En comptesd’això,estudiemelcasdegirlateralpur,fixant Cl = kl = 0mentre Cs vedonatperl’equació(38).Elmodeladimensionalesredueixaleshoresa

Definim

Perrecuperarelcasdegirconstantlescondicionsfixadessón φ1 = 0i φ2 = 1. Mantenintlesdefinicionsanteriorsperalsparàmetrespetits(peròamb ks substituïtper ks0),lesequacionsespodenescriurecoma

Elgirvariableésrepresentatpeltermequeinclou φ1 elqualapareixambl’ordre dominantal’equacióde X.Aixídoncs,homesperaqueelgirvariabletingui unefectesignificatiuenelmovimenten X.Totiaixò, φ1 i X nomésapareixen alesequacionsde Y i Z ambelsegonordrei,pertant,homesperaqueelgir variabletinguipocefecteenelmovimenten Y , Z

Utilitzantunapertorbacióestàndard,finsal’ordre O(ε) lessolucionssón

Observantque kl = 0resultaque c3 = c4 = 0ialeshoreslessolucionsde Y i de Z anteriorscorresponenalesequacions (21)–(23) finsal’ordre O(ε),mentre quelasolucióde X difereixdel’equació(21)enl’ordredominant.

Figura6: Trajectòriesadimensionalsde X, Y i Z enfuncióde T pera Cs variable(amb ω = 50):soluciónumèricacompleta(líniacontínua), solució O(ε0) (líniadepunts)isolució O(ε) (líniadepuntsiratlles): (a) L2 = 20;(b) L2 = 30m.

TimothyG.MyersiSarahL.Mitchell

Lafigura6mostraunacomparacióentrelessolucionsnumèriqueside pertorbaciódelmodelincloent-t’hielgirvariable.Lafigura6(a)télesmateixes condicionsinicialsques’havienfetserviralafigura3,peròaraamb Cs variant d’acordambl’equació (38) i ω = 50 rad/s.Lalíniacontínuaéslasolució numèricaileslíniesdiscontínuesindiquendiversosnivellsdelasolucióde pertorbació.Lacorba X mostraquealfinaldelatrajectòrialapilotas’ha mogutunamicamenysde0.6unitatsadimensionals,quecorresponauna distànciadimensionalde0 6ks0L2 2 ≈ 2 59 m.Comqueelviratgedimensional ésproporcionala L2,alafigura6(b)esrepresentaelmateixxutperòaraauna distànciade30 m.Elcanvide L2 provéd’unaugmentde ε = kdL2 iaixís’espera quelasoluciódepertorbacióperdiprecisió.Aixòésclarobservantlafigura, totiquelasolució O(ε) ésrelativamentprecisa(podríemaugmentaraquesta precisiótrobantelterme O(ε2)).Elviratgedimensionalalfinaldelrecorregut araésd’uns4.86 m.Aquestvalorésquasieldobledelcorresponentaunxut desde20 m iprovédeladependènciaaproximadamentquadràticarespectede ladistància.

Alafigura7(a)hihadibuixadesquatrecorbescorresponentsa ω = 30,40, 50,60 rad/s i L2 = 30 m (amblarestadecondicionscomalafigura3).Tal coms’esperava,augmentar ω faaugmentarelmovimentlateraldemanera que X(1) variade0.298a0.44quan ω augmentade30a60(idimensionalmentde2 9 m a4 3 m).Obviantelfregamentvariable,l’equació (29) indicaque l’incrementhauriadeseraproximadamentlineal x ∝ ks .Inclourelavariació delcoeficientdefregament,ambtruncament,faquel’augmentsiguinolineal. Perexemple,quan ω augmentade30a40, X(1) augmentaen0 052(dimensionalment0.5 m),peròaugmentant ω de50a60, X(1) augmentanomésen 0 04(dimensionalment0 4 m).Unaugmentde ω superiornoproduiràgaire variacióenelmoviment.Enspotajudaraentendreaixòlafigura7(b)que mostralavariacióde Cs alllargdelatrajectòria:amb ω = 30o40elvalor de Cs sempreaugmenta.Quan ω = 50elvalorde Cs estornaconstantcap alfinaldelvolipera ω = 60ésconstantdurantlameitatdeltempsdevol. Pertant,qualsevolxutamb ω> 60donaràunresultatsimilaralde ω = 60. Duentatermeaquestestudivasorgirlapreguntadequèéselquepresenten exactamentelsdiferentsgrupsderecercaquandibuixenlescorbes Cs Sp.En particularnoquedaprouclarcoms’interpreta Sp = Rω/|v|.Elsexperiments deAsai etal. [1]idePassmore etal. [12]considerenunapilotafixadaenuntúneldeventenelqual ω i v romanenconstants,demaneraque Sp prenun únicvalorperacadaexperiment.Elfregamentilaforçalateralesmesuren directament,unfetquedespréspermetcalcularelscoeficientsdefregament atravésdel’equació (2).Experimentsmés«realistes»considerenunxutreal d’unapilotaenunentorncontrolatidespréscalculenelscoeficientsadaptant lesdadesaalgunmodelmatemàtic.Perexemple,BrayiKerwin[2]monitoritzenelvold’unapilotaambduescàmeres.Lesequacionsdelmodelesresolen is’iteren,utilitzantcoeficientsdefregamentcomaparàmetresvariables finsqueestrobaunabonacorrespondènciaamblesdadesexperimentals.

Figura7: (a)alapartsuperior,trajectòriesadimensionalsde x enfunció de t pera Cs variable;(b)alapartinferior,gràfiquescorresponents a Cs enfunció Sp ,lalíniadiscontínuarepresental’equació (38),lalínia contínuagruixudaéslavariacióde Cs alllargdelatrajectòria.

Ambaquestmètodeesdeterminenvalorsconstantsperalfregamentfrontali lateralperaunxutdonat.Detotesmaneres,comqueaquestsvalorsprovenen d’ajustarlatrajectòriasencera,on Sp ésunafunciócreixent,elscoeficients handeseralgunamenademitjanaperalxutespecífic.Carré etal. [4]fan servirunatècnicasemblantonelscoeficientsdefregamentsónmitjanes,però lesgràfiquesesfanapartirdelvalorinicialde Sp (d’aquestamaneras’evita laconfusióenlavariacióde Sp).GoffiCarré[7, 8]escullencoeficientsde fregamentpertaldeminimitzarl’errordemínimsquadratsentrelasolució numèricailesdadesdelsexperiments,peròperreduirlavariacióde Sp limiten lesdadesalsprimers0 07 s devol.Griffiths etal. [9]utilitzenunsistema

TimothyG.MyersiSarahL.Mitchell

precísdeseguimentdelapilotaperòcalculenelscoeficientsamblafórmulade Wesson[14],quesuposaelfregamentconstant.Pertant,lesdiferentsdades queesdonenmostrenvalorsde Cs i Sp realsobépodenservalorsmitjans sobreunatrajectòriadonada(ambdiferentsmètodesdeferlamitjana).La figura8presentadosgrupsdecorbes,lescorbesdesotacorresponena Cs variableamb L2 = 30 m.Lalíniadiscontínuarepresentalatrajectòriafinsa t = 1.655 s (peracabara y ≈ 30 m)ilalíniacontínuaacabaa t = 0.693 s (al voltantde y = 15 m).Lescorbesdelapartsuperiorutilitzenunvalorconstant de Cs = 0.307,quevaserescollitperfercoincidirelresultatdelavariable Cs desprésde1 655 s.Lagràficaespresentadimensionalment,jaquetotesles modificacionsd’escaladepenendelatriade Cs .Toteslesaltrescondicions sónlesmateixesqueencasde ω = 50 rad/s delafigura7.Lacaracterístca importantésqueperatempsdiferentsde1.655 s lacorbaconstantde Cs té unaquantitatdeviratgediferent,fetqueindicaquesis’utilitzaunvalormitjà pera Cs ,aleshoreselseuvalorvariaràambladistànciadelpuntdexut(ala figuraelsxutsde15 m mostrenunadiferènciade10 cm enelviratge).Aixòés, sitoteslesaltrescondicionsestanfixades,ajustantunvalorconstantde Cs a lesdadesexperimentals,llavorsobtindremunrangdevalorsde Cs peraxuts fetsadistànciesdiferents.

Figura8: Comparaciódetrajectòriespera Cs variableipera Cs constant.

6Discussió

Enaquesttreballhemestudiatlesequacionstridimensionalsperalmoviment d’unapilotadefutboldurantelvol.Lasoluciónumèricaéstrivialperòaquesta nomostraladependènciadelproblemarespectedelsparàmetres.Peraquest motiu,s’hadesenvolupatunasoluciódepertorbacióqueharesultatmoltprecisa quanescomparaamblasoluciónumèrica.Enl’obtenciód’aquestasolucióel canvid’escalas’habasatenlahipòtesiqueelsjugadorsdefutboldonenmés efectelateralquepersobre(opersota)alapilota.Aixòespodriacanviar fàcilmentsiestudiéssim,perexemple,elmovimentd’unapilotadegolf,on l’efectepersobreopersotaéseldominant.L’anàlisirealitzadahapermèsfer unseguitd’observacionssobreelmovimentdelapilota.

Lesaproximacionsanalítiquesmostrenqueal’ordreprincipalelmoviment lateralésproporcionalalcoeficientdefregamentlateral ks ialadistància (vt)2 . Aixòexplicaelmotiupelqualelsxutsdefaltafetsdemésllunytenenmés viratge.Finsalprimerordreenelparàmetrepetit,elmovimentencadadirecció estàdescritperunaequaciódegrau4comamàximeneltemps.Elsestudis experimentalssovintaproximenlesdadesambunpolinomi.Perexemple,Carré etal. [4]mostrenunaconcordançaexcel.lentamblesdadesexperimentalssuposantquela x variaquadràticamentamb t.Aixòestàd’acordambelresultat referental’ordreprincipald’aquestestudi, x ≈ ks (vt)2/2,ipermetràcopsar correctamentelcomportamentdominantilasolucióperatempspetit.Bray iKerwin[2]suposenunadependènciaquàrticapera x, y, z:comqueuna quàrticacontéméscoeficients,hompotajustarlesdadesexperimentalsamb mésprecisió.Aquestafuncióestàenconcordançaambl’expressiódeprimer ordre.Peraquestaraóelsresultatsquepresentemaquínoesvancomparar inicialmentambdadesexperimentals:moltsestudishanmostratquelesdadespodenserbenaproximadesperfuncionsquadràtiquesoquàrtiques.Com queelsresultatsprenenaquestaforma,espotobtenirunabonaconcordança simplementescollintelscoeficientsadequats(iaixídeduintelsvalorsdels coeficientsdefregament).Detotesmaneres,pelsuggerimentd’unrevisor,hem comparatelsresultatsambelsde[4].Aixís’havistquehihalaconcordança esperadais’hanpogutdeterminard’unamanerasenzillaelsparàmetresdel vol.Defet,aixòmostrad’algunamaneraquelesequacionspodenserconsideradesindulgentsenelsentitqueunmodelpocprecíspotdonarencarauna bonaconcordançaambdadesexperimentals.Negliginttermes,perexemple, estudiantnoméselmovimentbidimensional,portaràalamateixaformade solucióqueelsistematridimensional,peròelscoeficientspolinomialsseran diferents.Comaconseqüència,unestudinumèricd’unconjuntd’equacions lleugeramentincorrecteseràcapaçdedonarunabonaconcordançaambles dadesexperimentals,peròelscoeficientsdefregamentcalculatsambaquesta solucióserandiferentsdelseuvalorreal.Peril.lustraraquestfet,combinem lesequacions (29) i (30) pertaldedeterminarunaexpressióde x comafunció de y,precisafinsal’ordre O(ε),

(50) onelstermes O(ε) estanentreclaus.Al’ordreprincipal,espotobservarel fetbenconegutque x varia,demaneraaproximada,quadràticamentamb y. Amesuraqueeltempsavança,id’aquestamanera y,elterme O(ε) creixen importànciaifaqueelvolesdesviïdelaformaquadràticaiaquestadesviacióés descritaperunaquàrtica.Elcoeficientcorrectede y 2 enl’equacióanterior és ks (1+w 2/v 2)/2.Donatunpolinomiques’ajustiamblesdadesexperimentals idonatsvalorsinicialsdelesvelocitats v i w,éspossiblecalcular ks simplement comparantelscoeficientspolinòmicsadequats.Detotesmaneres,sielmodel matemàticnegligeixelmovimenten z (fixant w = 0a (50)),aleshoreslapredicció de ks estaràafectadaperunfactor1 + w 2/v 2 respectedelseuvalorreal.

TimothyG.MyersiSarahL.Mitchell

Aleshoresòbviaments’had’anarambcompteal’horadetriarelmodel pertald’obtenirelscoeficientsdefregamentapartirdedadesexperimentals tridimensionals.Silapilotaésllançadaenuncampgravitacional(cosamésaviat difícild’evitar)ambefectelateral,aleshoress’haurand’utilitzarlesequacions tridimensionalsalcomplet,jaquelavelocitatverticaltéunefecteimportanten elmovimentlateral.L’excepcióaaquestanormaésquanlapilotaésllançada ambvelocitatzeroenladirecció x inomésambefectepersobre(opersota); aleshoresunestudibidimensionalenelpla y-z seràsuficient.Comque Cs apareixpelmateixefecteque Cl,noméss’hadedeterminarunad’aquestes duesquantitatsil’experimentdos-dimensionalensdonaràtotalainformació necessària.

Enlasecciófinals’hainvestigatl’efectequetélavariacióde Cs (o Cl)acausa delgirdurantelvol.Elsestudisnumèricsgeneralmentsuggereixenunvalor constant,sovintescollitperdonarelmillorajustalesdades.Elsresultatsen aquestestudimostrenquelavariacióde Cs provocauncanvienrelacióamb lestrajectòriespredites.Totiqueéspossibletriarunvalorconstantmitjà, aquestvalorvariaràamblallargadadelatrajectòria.Comqueelcoeficient defregamentésunafunciódelapilotaidelespropietatsdel’aire,inodela llargadadelvol,aquestresultatésfísicamentpocrealista.Unproblemaqueva sorgirenaquestapartdel’estudivaserlainterpretaciódelgir.Perdeterminar Cs entermesde Sp espotrealitzarunexperimentonlatrajectòriadelapilota defutbolsesegueixambalgunequipdecapturademoviment.Lacomparació ambelsresultatsdelmodelmatemàticportaaunvalorde Cs peraun Sp donat, peracadaexperiment.Detotesmaneres,comque Sp,defet,creixdurantel volnoésclarquèesvoldirambelvalorcitat.Excepcionsaaquestanormasón elsexperimentsdutsatermeambunapilotaimmòbilenuntúneldevent,cas enquè Sp espotmantenirconstant;vegeu,perexemple,[1,12].

Elsaltbenconegutenelcoeficientdefregament,quepotproduirunarotació ensentitcontrarienaltresesports,nos’haconsideratenaquestarticlejaqueel movimentd’unapilotadefutboltéllocperavalorsdelnúmerodeReynoldsper sobredelatransició[10].Detotesmaneres,vallapenafernotarquelatransició téllocperavalorsde Re mésaltscommésllisaéslapilota.Comqueladensitat del’airedisminueixambl’altitud(ipertant,tambéhofa Re),aixòpodriaser unfactorimportantenelmovimentd’unapilotallisaenestadissituatsamolta altitud,comaraeldeJohannesburg.Defet,durantlaCopadelMóndel2010, enquèesvaferservirlapilotaJabulani(unapilotallisasensecostures),hiva havermoltescrítiquessobreelsvolsaparentmenterràticsdelespilotes.Per exemple,elseleccionadord’Anglaterra,FabioCapello,vaafirmarquelapilota escomportavad’unamaneraestranyaagranalçadasobreelnivelldelmar;el davanterbrasilerFabianovaafirmarquecanviavademaneraimprevisiblede direccióquananavaperl’aire;vegeu[15].

Acontinuacióesdiscuteixsil’elecciódelapilotapotdonaralgunavantatge aunequip,ienparticularsil’alturahipotintervenir.Del’equació (29) espot veurequeelviratgeenladirecció x ésproporcionala ks = ρACs /(2m).Elvalor deladensitatdel’aire ρ decreixambl’altitud.Enestadisagranaltitud,comel

deJohannesburg,a1800 m, ρ ≈ 1 04 kg/m3 ésaproximadamentun20%més baixaqueanivelldelmar, ρ ≈ 1.29 kg/m3.Pertant,unequipacostumatajugar anivelldelmaresperaràun20%mésdeviratge.Peril lustrarladiferènciamés clarament,alafigura9esmostrentrestrajectòriesperaxutsidènticsamb ρ = 1 04,1 19i1 29 kg/m3 (elsdosúltimsvalorssónelsadequatsperaMadrid iBarcelona,respectivament).Elsvalorsinicialssón v = 36 m/s i L2 = 35 m,el coeficientdefregamentésconstant, Cs = 0.34,ilesaltrescondicionssónles mateixesqueenlesfiguresprèvies.Silapilotaesxutainicialmentanivelldel paldelaporteria,aleshoresunavelocitatenladirecció x de 15.16 m/s portaa ungolnomésanivelldelmar,quan ρ = 1 29(utilitzemaquílasoluciónumèrica jaque x noesvaincloureenlasoluciódepertorbacióidepassadaaquest xutverificalasoluciódepertorbació).ElmateixxutfetaMadridpassariade llargdelaporteriauns1.3 m mentrequeaJohannesburgfallariaperuns3.3 m. Hörzer etal. [10]vanprediruncomportamentsimiliaralessevessolucions numèriques.

L’avantatgedelasolucióanalíticapresentadaenaquestarticleésqueno nomésmostraexplícitamentl’efectedeladensitatdel’aire,sinóquetambé mostraladependènciarespected’altresvariables.Perexemple,comqueel viratgeésproporcionala ρACs ,elcanvienelcomportamentdelapilotadegut al’altitudespotobtenircanviantelcoeficientdefregament.Latrajectòria pera ρ = 1.29alafigura9potfer-seidènticaalacorbade ρ = 1.04posant Cs = 1 04 × 0 34/1 29 ≈ 0 274.Aixòésuntemaimportantactualmentperals fabricantsdepilotesdefutbol(impulsatperlaCopadelMóndeSud-àfrica del2010)quevolenfabricarpilotesquetinguinelmateixcomportamenta diferentsaltituds.

Figura9: Diferènciesentrajectòriesadiferentsaltituds.

Finalment,quedalapreguntadesiaquestaanàlisipotmarcardiferència alapràctica.Lasolucióanalíticamostraclaramentelsfactorsqueafectenel

TimothyG.MyersiSarahL.Mitchell

voldelapilota.Posademanifestqueelsequipsquejuguenalacostaestan acostumatsaunviratgemésgranqueelsequipsquejuguenagransaltituds, jaqueladensitatdel’aireolarugositatdelapilotaredueixenelviratge.En conseqüència,desprésdelareunióquevatenirllocaJohannesburgelgener del2011esvasuggerirqueelBidvestWitsutilitzésunapilotallisaperals partitsjaqued’aquestamaneras’aconseguiriaelcomportamentmésallunyat delqueesperenelsequipsquenormalmentjuguenenaltitudsmésbaixes.En canvi,enelsentrenamentsperapartitsaforahauriendeferservirunapilota rugosa.Elsequipsdecostahauriend’aplicarl’argumentcontrariitriarpilotes rugosesquanhandejugarambequipsd’altitudsgrans.Ésclarquenoespoden predirtotselsfactorsqueafectaranlasortdelsequips,peròvallapenade notarqueabansdelareuniódeJohannesburgelsWitsnohavienguanyaten vuitpartitsconsecutius.Enelseuprimerpartitacasadesprésdelareunió, quevanjugarambunequipdecosta,vanguanyarper6-0.Finsalfinaldela temporada2011vanperdrenomésunpartitacasa,quevaserunpartitde Copa,onl’equipdecasanopotposarlapilota.Desafortunadament,nohovan fertanbéenelspartitsforadecasa.

Agraïments

LarecercadeT.G.MyershatingutelsuportdelprojecteIndustrialapplicationsofmovingboundaryproblems(MarieCurieInternationalReintegration Grant,núm.FP7-256417)idelMinisterideCiènciaiInnovació,ajutMTM201017162.S.L.MitchellagraeixelsuportdelMathematicsApplicationsConsortium forScienceandIndustry(MACSI, www.macsi.ul.ie)finançatperlaScience FoundationIrelandMathematicsInitiative,grant06/MI/005.

Referències

[1] Asai,T.;Seo,K.;Kobayashi,O.;Sakashita,R. «Fundamentalaerodynamicsofthesoccerball». SportsEngineering,10(2007),101–110.

[2] Bray,K.;Kerwin,D. «Modellingtheflightofasoccerballinadirectfree kick». JournalofSportsSciences,21(2)(2003),75–85.

[3] Bray,K.;Kerwin,D.G. «Simplifiedflightequationsforaspinningsoccer ball».A: Reilly,T.;Cabri,J.;Araújo,D. (ed.). ScienceandFootballV:The ProceedingsoftheFifthWorldCongressonScienceandFootball.Londres. NovaYork:Routledge,2005,39–44.

[4] Carré,M.J.;Asai,T.;Akatsuka,T.;Haake,S.J. «Thecurvekickofa football ii:flightthroughtheair». SportsEngineering,5(2002),193–200.

[5] Carré,M.J.;Goodwill,S.R.;Haake,S.J. «Understandingtheeffect ofseamsontheaerodynamicsofanassociationfootball». Proceedings oftheInstitutionofMechanicalEngineers,PartC:JournalofMechanical EngineeringScience,219(2005),657–666.

[6] Dupeux,G.;LeGoffA.;Quéré,D.;ClanetC. «Thespinningballspiral». New.J.Phys.,12(2010),093004.

[7] Goff,J.E.;Carré,M.J. «Trajectoryanalysisofasoccerball». Am.J.Phys., 77(11)(2009),1020–2017.

[8] Goff,J.E.;Carré,M.J. «Soccerballliftcoefficientsviatrajectoryanalysis». Eur.J.Phys.,31(2010),775–784.

[9] Griffiths,I.;Evans,C.;Griffiths,N. «Trackingtheflightofaspinningfootballinthreedimensions». Meas.Sci.Technol.,16(10)(2005),2056–2065.

[10] Hörzer,S.;Fuchs,C.;Gastinger,R.;Sabo,A.;Mehnem,L.;Martinek,J.; Reichel,M. «Simulationofspinningsoccerballtrajectoriesinfluencedby altitude».8thConferenceoftheInternationalSportsEngineeringAssociation(ISEA). ProcediaEngineering,2(2)(2010),2461–2466.

[11] Oggiano,L.;Sætran,L. «Aerodynamicsofmodernsoccerballs». Procedia Engineering,2(2)(2010),2473–2479.

[12] Passmore,M.A.;Tuplin,S.;Spencer,A.;Jones,R. «Experimentalstudies oftheaerodynamicsofspinningandstationaryfootballs». Proceedings oftheInstitutionofMechanicalEngineers,PartC:JournalofMechanical EngineeringScience,222(2)(2008),195–205.

[13] Rigsby,B. «Thehistoryofthesoccerball».Disponiblea http://www. soccerballworld.com/History.htm#Early.

[14] Wesson,J. Thescienceofsoccer.Bristol.Filadèlfia:IOPPublishingLtd., 2002.

[15] Wikipediacontributors.«AdidasJabulani».Wikipedia,TheFreeEncyclopedia.Datadel’últimarevisió:1degenerde2015.Disponiblea http:// en.wikipedia.org/wiki/Adidas Jabulani.

TimothyG.Myers CentredeRecercaMatemàtica CampusdeBellaterra,EdificiC 08193Bellaterra Barcelona,Espanya tmyers@crm.cat

SarahL.Mitchell MACSI DepartmentofMathematicsandStatistics UniversityofLimerick Limerick,Ireland sarah.mitchell@ul.ie

ButlletídelaSocietatCatalanadeMatemàtiques Vol.30,núm.2,2015.Pàg.193–205. DOI:10.2436/20.2002.01.63

Sèriesdepotències(aleatòries)

JoaquimOrtega-Cerdà

Resum: Laconstrucciódefuncionsaleatòriesambpropietatsinteressantsésuntema dellargatradicióenlesmatemàtiques.Darrerament,iresseguintl’estudidelsvalors propisdematriusaleatòries,s’estàduentatermel’estudidelszerosdepolinomisi funcionsaleatòriesholomorfes.

Paraulesclau: polinomisaleatoris,funcionsanalítiquesgaussianes.

ClassificacióMSC2010: 30B20,26C10,30C15,15B52.

1Introducció

Enl’anàlisi d’unafunció,ésfreqüentdescompondre-laensuperposicióde funcionssimplesiaquestadescomposiciós’utilitzaperarribaraesbrinar propietatsdelesfuncions.Aixòéslabasedel’anàlisideFourier,delessèries depotències,delesondetes,delessèriesdeDirichlet,etc.

Elprocésinvers,la síntesi,construeixfuncionsapartirdelasuperposició defuncionssimplespertald’obtenirfuncionsambpropietatsdesitjades.

UnexempleclàssicéslafunciódeWeierstrass: f(x) = n≥1 an cos(bnx),

amb a< 1i ab ≥ 1.Aquestaésunafunciócontínuaa R noderivableencap punt.

Devegades,nosabemcomtriarelscoeficientsperferunacombinació defuncionssimplesambpropietatsdesitjadesielquefeméstriaral’atzar!

Aquesthaestatunmecanismepopularenlasegonameitatdelsegle xx utilitzat pergenerarfuncionsambpropietatsprefixades.Unexempleparadigmàtices trobaenelllibredeKahanedesèriesdefuncionsaleatòries;vegeu[8].

Articlebasatenlalliçóinauguraldelcurs2014–2015alaFacultatdeMatemàtiquesiEstadística delaUniversitatPolitècnicadeCatalunya.

Estudiaremaraunproblemaaleatoridiferent.Volemgenerarpuntsaleatoris ambunescertespropietatsdedensitatiseparacióprefixada.Unaformade generar-losquehaguanyatpopularitatenladarreradècada(vegeu[6, 13]), totiquehihaantecedentsmoltmésanticscomara[7, 9],éslasegüent:es tractadetriarpolinomis,o,mésgeneralment,funcionsanalítiques,mitjançant unaeleccióaleatòriadelsseuscoeficientsdeformaindependentiobservar elszerosd’aquestspolinomis.Elspuntsaleatorisgeneratsd’aquestamanera tenenpropietatsestadístiquesderepulsiólocalmoltinteressantsquehanfet quesiguinestudiatscomapossiblesmodelsfísicsdepartículesambrepulsió (fermions);vegeu[1].

2ElspolinomisdeKac

Comencemambuncassenzill.Consideremelpolinomialeatori:1

on ajaj , j = 0,...,n sónvariablesaleatòriesindependentsidènticamentdistribuïdes, ajajaj NC(0, 1).Calculemelszerosde pn

n: z1

1z1,...,znznzn.Quinaésla sevadistribució?Podemobservar-neunexemplealafigura1.Enaquestcas semblaclariespotdemostrarqueelszerosd’aquestspolinomisesconcentren uniformementdistribuïtsentorndelcercleunitatdeformamajoritària.Aquests sónelsanomenats polinomisdeKac.

Figura 1: ElszerosdelspolinomisdeKac. 1Marquemennegretaelselementsaleatoris.

Enaquesttipusderesultat,elfetque aiaiai siguiunavariablealeatòrianormal ésmoltconvenientdesd’unpuntdevistatècnic,perònoésimprescindible. Defet,hiharesultatsanomenats d’universalitat quegaranteixenque,independentmentdelatriadevariablesaleatòriesperalscoeficients,sempreque siguinindependentsiidènticamentdistribuïdes,elsresultatsseranmoltsimilars.Siaquestesfossintoteslespossibilitats,l’interèsacabariaaviat.Elqueés rellevantéslanormalitzacióquetriemdelscoeficients.Veuremque,aleshores, elresultatvariamoltsubstancialment.

ConsideremunavariantdelspolinomisdeKac.Triemelspolinomisaleatoris (dits deWeyl)ambunanormalitzaciódelscoeficientsdiferent:

on ajajaj , j = 0,...,n sónvariablesaleatòriesindependentsidènticamentdistribuïdes ajajaj NC(0, 1).Calculemelszerosde pnpnpn: z1z1z1,...,znznzn.Lasevadistribució, queobservemenlafigura2,semblaararepartir-seenundiscderadi √n,on n éselgraudelpolinomi.

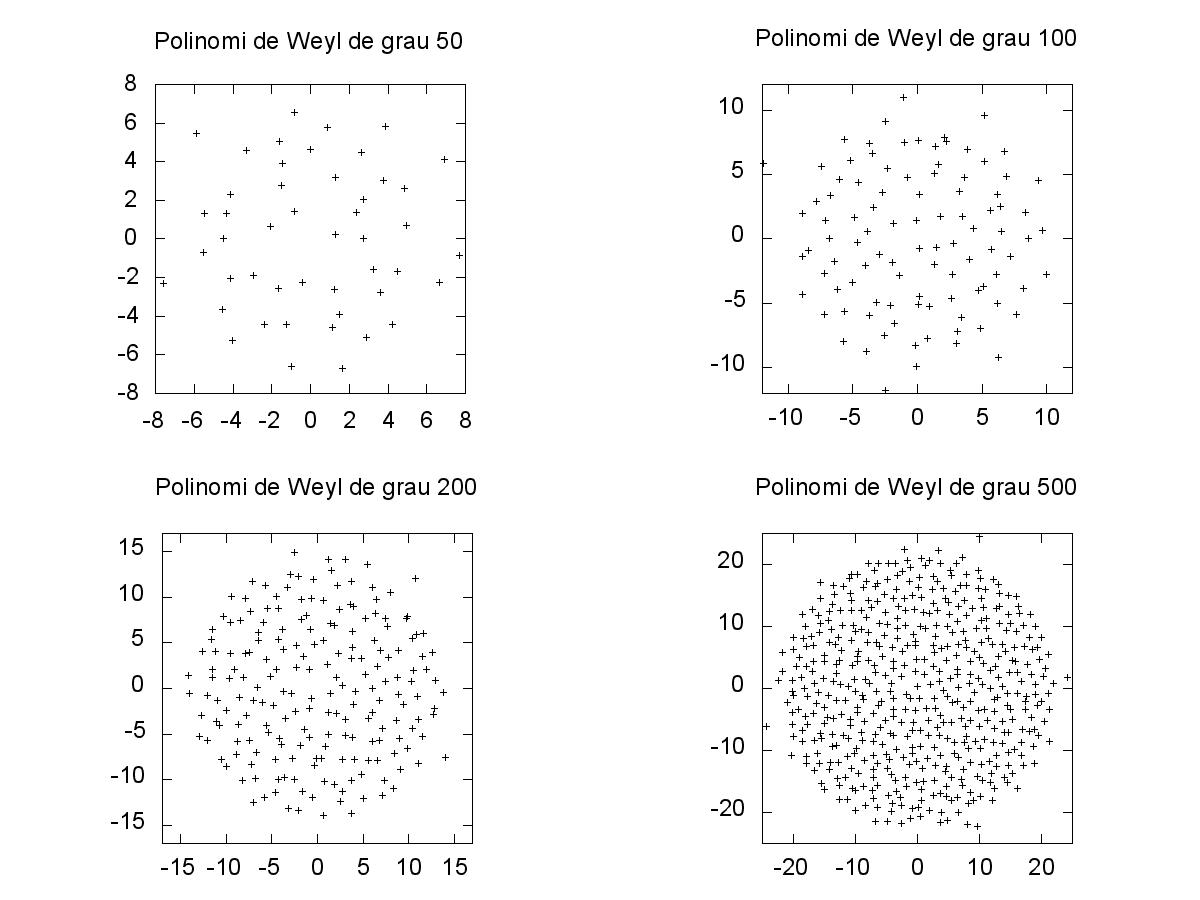
Figura 2: ElszerosdelspolinomisdeWeyl.

Ladiferènciaenladistribuciódelszeros,entreelspolinomisdeKaciels deWeyl,espotexplicarperlaraóquelesfuncions fn(z) = zn formenuna baseortonormaldel’espaideHardydefuncionsholomorfeseneldiscunitat ambnorma f 2 = 1 0 |f(e2πiθ )|2 dθ i,encanvi,lesfuncions gn(z) = zn/√n!, utilitzadesenladefiniciódelspolinomisdeWeyl,formenunabaseortonormal del’espaideFockdefuncionsenteres g talsque g 2 = C |g(z)|2e−|z|2 dm(z) Tantl’espaideHardycoml’espaideFocksónespaisdeHilbertdefuncionsamb nuclireproductor,iveuremqueladistribuciódelszerosdelesfuncions aleatòriesaixíconstruïdesespotcalcularapartirdelnuclireproductor.

Vèiemabansalgunacaracterísticaencomúquetenenelszerosdeles funcionsanalítiquesaleatòriesindependentmentdelanormalitzaciótriada. Ladistribuciódelspuntsdinsdeldisc(oapropdelcercle,enelcasdels polinomisdeKac)noésarbitrària.Femun zoom delszerosdelspolinomis deWeylicomparem-losambelmateixnombredepunts,peròdistribuïts uniformementiindependentenelquadrat [ 15, 15] × [ 15, 15],comhemfet enlafigura3.

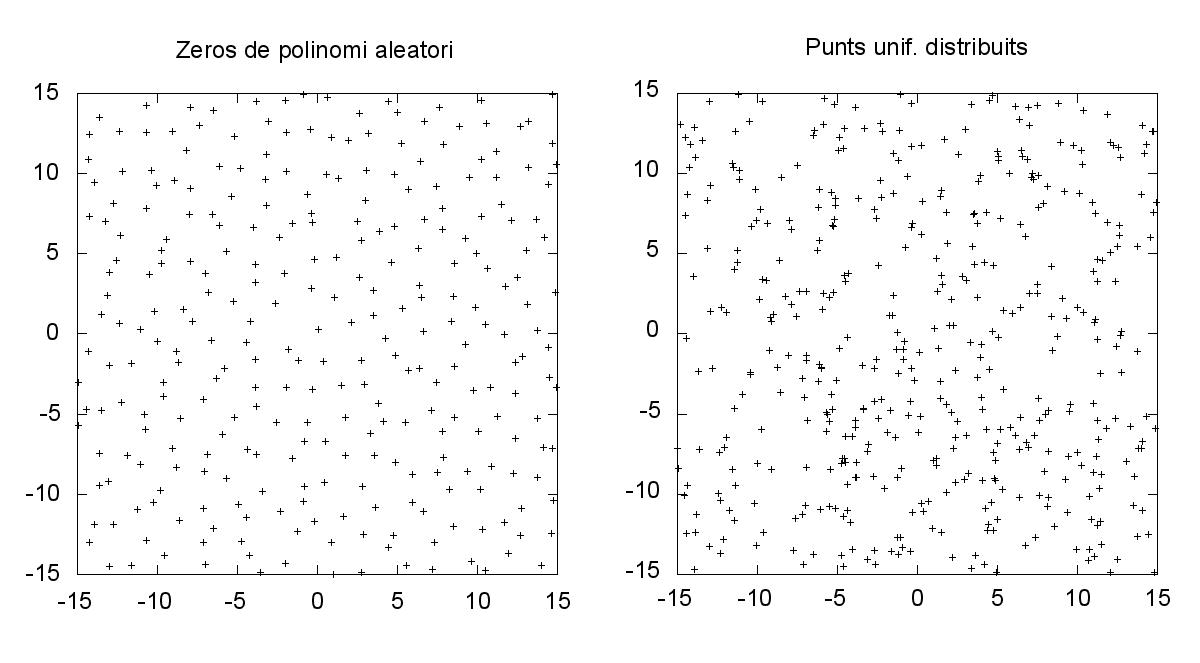
Figura 3

Observemqueelszerosdelspolinomisaleatorissemblentenirmés«estructura»iexhibeixenunarepulsiólocal.Tambés’observaquenohihaforats notables.Totplegatsemblaunadisposiciómésuniforme. Compararemaquestprocésdepuntsaleatorisambunaltredebenconegut, elprocésdeGinibre.Consisteixaprendreunamatriudedimensió n × n ambtotselsseuscoeficientsquesiguinvariablesaleatòriesidènticament distribuïdesiindependentsambdistribuciógaussiana: NC(0, 1) iaobservar elsvalorspropisd’aquestamatriu.

Ginibrea[2]vaestudiarl’espectred’aquestamatriu(quediagonalitzaamb valorspropisdiferentsforad’unconjuntexcepcionaldematriusdeprobabilitat zero).Vaobservarqueelsvalorspropissónpuntsenelplacomplexambuna distribuciómoltsimilaralszerosdelspolinomisdeWeyl.Enlafigura4,veiem depropladistribuciódelszerosdelpolinomialeatoriil’espectredelamatriu aleatòria.

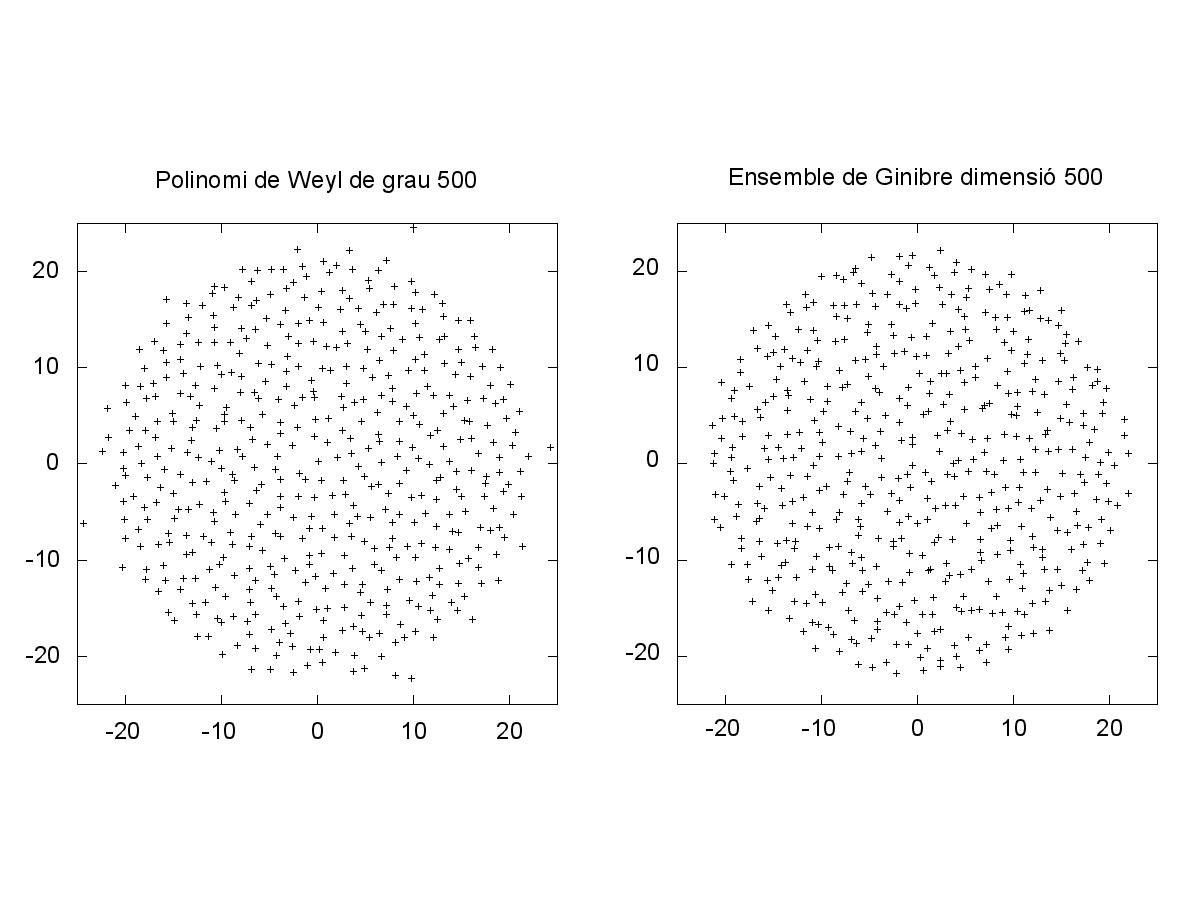
Sicomparemelszerosielsvalorspropisglobalment,comenlafigura5, observemunadistribuciómoltsimilar,ambunadiferènciasubtil.Enelconjunt deGinibre,latransicióentreeldiscpledezerosielseucomplementsembla mésnítida,mésabrupta.EnelszerosdelpolinomideWeyl,semblaquehiha unaregiódetransicióonhihaunspocszeros.Miraremdejustificaraquesta observació.

Elsdosprocessosdepuntsaleatoris,eldeGinibreieldelszerosdelpolinomideWeyl,admetenunaextensióainfinitspunts.Enelcasdelspolinomisde Weyl,estractadelszerosd’unafuncióenteraaleatòria:

Elcasdevalorspropisdematriusdedimensionsinfinitesésmésdelicattècnicament.Enqualsevolcas,unapropietatencomúquetenenaquestsprocessos d’infinitspuntsésquesóninvariantspertranslacions,ésadir,laprobabilitat detrobarunnombredeterminatdezerosenunconjunt A ien A + z ésla mateixaperatot z.Defet,juntamentambelprocésdePoissonclàssic,són elsúnicsprocessos«naturals»queconecquetenenaquestainvariànciaper translacions.Això,naturalment,elsfamoltatractius.

3Un detour perlesmatriusaleatòries

Lamotivacióperestudiarelsvalorspropisdematriusaleatòriesvedelproblemadeladifusió(scattering)nuclear.Wigner,enelsanyscinquanta,va proposarl’estudidevalorspropisaleatorispermodelarl’estatexcitatd’alguns nuclisatòmicsgrans.VegemalgunsexemplestretsdelllibreclàssicdeMehta

(vegeu[10])sobrematriusaleatòries,quesegueixsentunabonareferència. Estractaderessonànciesdedifusiócorresponentsanuclisdegadolini,torii urani,representadesenlafigura6(tretade[10]). Gadolini156Tori232iUrani238

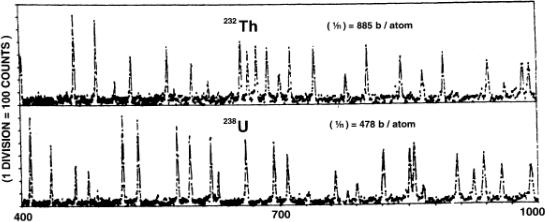
Enlafigura7(tretade[10]),comparemladistànciaentreressonànciesde difusióil’espaientrevapsdelGOE(GaussianOrthogonalEnsemble),quesón matriussimètriquesrealstalsquelessevesentradestriangularssuperiorssón variablesaleatòriesindependentsgaussianesrealsidènticamentdistribuïdes.

L’estudidelsvalorspropisdematriusaleatòrieshaesdevingutuncampd’estudiimmens(ambmésde2700entradesalMathSciNetdesdel’any2000).Gran partdelasevapopularitatésdegudaalesrelacionsamblafísicamatemàtica, peròtambéambaltrescampspotserméssorprenents.

Estudiantladistribuciódelszerosdelafunció ζ deRiemann,Montgomery (vegeu[11])conjecturàunacertarepulsiólocalentreaquestszeros.ÉsllegendàrialatrobadaambelfamósfísicnuclearDyson,quelivafernotarlasimilitud d’aquestaqüestióambladistribuciódelsespaisentreelsvalorspropisde matriusaleatòriesdelGUE(GaussianUnitaryEnsemble).Odlyzkoa[12]experimentanumèricamentaquestaconjecturacalculantmilionsdezerosdela ζ de RiemmanihocomparaambladistribuciódelsvalorspropisdelGUE,comen lafigura8(tretade[10]),idónasuportallligamconjecturatentrelacorrelació delszerosdelafunció ζ ilacorrelacióentreelsvalorspropisdematriusdel GUE.

8

4Interpretaciódelsresultatsnumèrics

4.1Larepulsiólocal

Intentementendrealgunsdelsfenòmensobservatsenlesfiguresanteriors. Unaexplicacióheurísticadelperquèdelarepulsiólocaléslasegüent:

Proposició 1 Si p(z) = n i=1(z zi) técoeficients ak, i.e.: p(z) = zn + an 1zn 1 +···+ a1z + a0,

aleshoresl’aplicació T(z1,...,zn) = (a0,...,an 1) téjacobià i<j |zi zj |2

DemaneraquelamesuradeLebesgue«uniforme»sobreelscoeficientses transportaper T aunamesurasobreelszerosambfunciódedensitat0,sidos zerossóniguals.

Aixòfaquelaprobabilitatdetrobarzerosmúltiplessiguizeroiquela probabilitatdetrobarzerosmoltapropl’undel’altresiguimoltpetita,jaque elscoeficientsdelspolinomissónvariablesindependentsilocalmentlamesura deprobabilitatésuniformeenelscoeficients.

IntentemveurearaperquèelszerosdelspolinomisdeWeylesdistribueixen deformaaparentenundisc.Lamaneraméssimpled’entendreaixòésestudiar ladistribucióenmitjanadelszeros.Éselqueesconeixcoma primeraintensitat delprocésdepunts

4.2Laprimeraintensitat

Suposemquetenimunafuncióaleatòriadelaforma f f f(z) = ∞ k=0 mkakakzk , on mk sóncoeficients(deterministes)prefixatsi aka ak variablesaleatòriesindependents, akakak NC(0, 1).Laprimeraintensitat ρ éslamesuramitjanadels punts.

Mésformalment,peracadarealitzaciódelszeros z1,z2,... ,anomenen µ µ µ alamesuraempíricadelszeros: µ µ µ = i δzi iz ,on δzizi ésladeltadeDiracenel

punt zizizi.Podemdefinir laprimeraintensitat ρ perdualitatcomunamesura actuantsobrefuncionscontínuesasuportcompacte:

hdρ := E hdµ dµ dµ,h ∈Cc (C),

on E denotal’esperança.Pertant,podeminterpretarque ρ = E(µ µ µ).Volem calcular ρ,queensdonaràunaprimeraaproximacióenmitjanadeladistribució delszeros.

Vegemaraunafórmulaexplícitapera ρ.Prenem fn(z) = mkzk idefinim

K(z,w) = n fn(z)fn(w).

Observemque,si (fn) ésunabaseortonormaldefuncionsd’unespaideHilbert defuncionsholomorfesambnuclireproductor,aleshores K coincideixamb elseunuclireproductor, i.e. f(z) = f(w),K(z,w) .Ésoportúremarcarque nonecessàriament (fn) hadeserlabaseortonormaldecapespaideHilbert, potsernitansolssónindependents.Però,enelcasdepolinomisdeKacoen elsdeWeyl,síquehosón,comjahemindicat.

Teorema 2 (fórmulad’Edelman-Kostlan). Escompleix

K(z,z).

Prova. PresentemunaprovasimplificadadegudaaSodin;vegeu[13].Sabem que,peratota f ∈H (C),

Prenemara f f f aleatòria f f f(z) =

Utilitzantaraque f f f(z) ésunavariablegaussianaambmitjana0,esveuimmediatamentquelavariànciaés K(z,z). E|f f f |2 = n |fn(z)|2 = K(z,z).

Pertant,si a a a ésunavariablealeatòriaambdistribució NC(0, 1),tenim ∆E log |f f f |2 = ∆E log |a a a|2 + ∆E log K(z,z) = ∆ log K(z,z), atèsque a a a ésindependentde z i E log |a a a|2 ésconstanti,pertant,harmònica. D’altrabanda, K(z,z) ésdeterminista. ✷

RecordemelcasparticulardelspolinomisdeWeyl:

Ara,

Perlafórmulad’Edelman-Kostlan,laprimeraintensitatdelspolinomisdeWeyl és:

Ginibrea[2]vacalcularlaprimeraintensitatdelconjuntdeGinibre(matrius ambentradesgaussianes)iresulta:

Aquestesduesintensitatssónfuncionsradialsquetenenunatransiciómolt ràpidad’1a0,comveiemenlafigura9.Enparticular,elszerosdelspolinomis deWeyltenenunatransiciólleugeramentméslentaqueelsvalorspropis.

9

Eltercergràficdelafigura9explica,pertant,perquèveiemalgunzeromés enelspolinomisdeWeylqueenelconjuntdeGinibreforadeldiscones concentren.

5Puntscríticsizeros

Enelspolinomisaleatoris,nonoméss’estudialadistribuciódelszeros,sinó quetambés’hanestudiat,perexemple,elspuntscrítics.Unexempleeltrobem enl’estudidelspolinomisel lípticsfetperHanina[3].

Figura 10: Zerosipuntscríticsdepolinomisaleatoris,cortesiadeBoris Hanin.

5.1Elspolinomisel.líptics

Consideremelspolinomis pnpnp delaforma:

Elszerosesdistribueixenen C demaneraque,sifemlaprojeccióestereogràfica, quedendistribuïtsuniformementenl’esferaunitat.

ComparatsambladistribuciódelszerosdelspolinomisdeWeyl,quetendiencapaunadistribuciódepuntsinvariantpertranslacions,ladistribució delszerosdelspolinomisel lípticsésinvariantpertransformacionsdeMöbius. Perjustificaraquestfet,podríemcalcularlaprimeraintensitatdelszerosdels polinomisel.lípticsmitjançantlafórmulad’Edelman-Kostlan,ilaintensitatresultaserunmúltiplede (1 +|z|2) 2.AquestamesuraéslamesuradeLebesgue enl’esferatransportadaalplaperlaprojeccióestereogràficai,pertant,és invariantperlestransformacionsdeMöbius.Aixònoacabadejustificardel totqueelszerossiguininvariants,jaquenoméshohemvistperalaprimera intensitat(lamitjanadelszerosésinvariant).Peròhihaunresultatsorprenent derigidesadelszerosdefuncionsanalítiquesgaussianes(vegeu[13,teorema2])queimplicaquetoteslespropietatsestadístiquesdelszerosqueden determinadesperlaprimeraintensitat,enparticular,lainvariància.

Comparemelszerosdelspolinomisielspuntscríticscomesveuenla figura10,onelspuntscríticsestanrepresentatsperunquadratielszeros,

perunpunt.L’origenestàrepresentatperunestel.S’hiobservaque,siens allunyemdel’origen,elszerosielspuntscríticsestrobenaparellatsi,defet, simesuremladistànciaentreells,ésaproximadament1/n,on n éselgraudel polinomi.Intentemdonararaunaexplicaciód’aquestfet.Perfer-ho,unaidea potentésbuscarunmodelfísicdelproblemamatemàtic;aixòpermetguanyar intuïcióil’argumentquedonemespotformalitzarfinsaunaprovarigorosa, quepodeutrobara[3],perexemple.

5.2Heurísticaelectrostàtica

Donemunajustificacióheurísticadel’aparellamentdezerosipuntscrítics:

• Espotveureque,ambprobabilitatun,elszerossónseparats,iunpetitcàlculutilitzantlafórmulad’Edelman-Kostlanindicaqueesdistribueixenuniformementenl’esferadeRiemann,uncopfetalaprojecció estereogràfica.

• Consideremelpotencialelectrostàticaleatori u u u = 1 2π log |pnpnpn|.Escompleix ∆u u u = n j=1 δajaj nδ∞.Aixòs’interpretacomuncampelectrostàticen l’esferadeRiemanngeneratper n càrreguespositivessituadesenels zerosdelpolinomialeatoriiunacàrreganegativadepes n enelpolnord (quecorresponalpuntdel’infinit).

• Unpuntcríticdelpolinomicorresponaunpuntonelgradientdelpotencialelectrostàtics’anul la,ésadir,aunpuntd’equilibridelcamp elèctric.

Enunpuntd’equilibri,hiactuentrestipusdeforcesques’handecompensar:

• Laforçadelacàrreganegativadelpuntdel’infinit.Ésproporcionala n

• Laforçadelacàrregapositivadelapartículaaleatòriaméspropera.És proporcionala1/r ,on r ésladistànciaalapartícula.

• Laforçadelesaltrescàrregues.Aquestesestandistribuïdes«uniformement»alvoltantdelpuntd’equilibri,iunavariantdelteoremacentral dellímitpermetveurequeaquestaforçaésproporcionala √n,ésadir, negligiblerespectealaforçadelacàrregaprovinentdelpolNord.

Pertant,percompensartoteslescàrregues,calquelacàrregapositivamés properaalpuntcríticestiguiaunadistància1/n i,aproximadament,enel segmentqueuneixelpuntcríticil’origen.

Aquestraonamentheurísticestrencaapropdel’origen(elpolSud,enla representacióestereogràfica),onlaforçaexercidaperlacàrregadelpolNord észero.Efectivament,s’observaquel’aparellamentdezerosipuntscríticses trencaapropdel’origen.

Aquestpuntresultacuriós,perquè,d’entrada,havíemcomentatqueels zerosereninvariantspertransformacionsdeMöbius.L’explicacióésque,en definirelspuntscrítics,estemprivilegiantl’origen.

6SèriesdeDirichletaleatòries

Vegem,finalment,coml’estudidelszerosdefuncionsaleatòriesnoesredueix asèriesdepotències,sinóquetambéespotestendreasèriesdeDirichletaleatòries.LacuriositatquefemnotaracontinuacióésdegudaaHelson(vegeu[5]) iestàdesenvolupadaa[4].Consideremlafunciósegüent:

f f f(s) = n≥1 χ χ(n)n s ,

on χ χ : N → T ={z ∈ C, |z|= 1} ésuncaràcteraleatori.Uncaràctersatisfà χ(n · m) = χ(n) · χ(m).Pertant,siprescrivimelvalorde χ sobreelsprimers: χ(2),χ(3),χ(5),... ,determinem χ deformaúnica.

Laprobabilitatqueintroduïmenl’espaidecaràcterséslasegüent:prenem χ(2) unpuntde T ambdistribucióuniforme.Independentment, χ(3) tambéambdistribucióuniforme,iaixíambtotselsprimers.

Identifiquem,doncs,elscaràctersambpuntsde T∞ iintroduïma T∞ la mesuradeprobabilitatproducte.Delamateixamaneraquehavíemfetambles sèriesdepotènciesaleatòries,podemconsiderarunspesos an deterministesi lafuncióaleatòria f f f(s) = n≥1 anχ χ(n)n s

6.1LahipòtesideRiemannquasisegurament

Diemque (an) éstotalmentmultiplicativa,si a1 = 1i anm = anam pera tot n, m.Peraqualsevol a> 0,elsemiplà (z)>a esdenotaper C+ a .Helson vaprovarelteoremasegüent:

Teorema 3. Si (an) éstotalmentmultiplicativaide 2,aleshoreslasèrie fχfχfχ(s) = n anχ χ(n)n s ésconvergentquasiseguramentcapaunafunciósensezeros a C+ 0 .

Unaconseqüènciagairebéimmediataaplicantelteoremaanteriora an = n 1/2 ε peraqualsevol ε> 0és

Corol.lari 4 (Helson). QuasiseguramentlafunciódeRiemann ζχ

s

(s) = n

ésconvergenta C+ 1/2 inotézerosa C+ 1/2.

Agraïments

L’autoragraeixelsuportdelprojectedelMinisterid’EconomiaiCompetitivitat MTM2014-51834-Pidelprojecte2014-SGR-289delaGeneralitatdeCatalunya.

Referències

[1] Berman,R.J. «Determinantalpointprocessesandfermionsoncomplex manifolds:largedeviationsandbosonization». Comm.Math.Phys.,327(1) (2014),1–47.

[2] Ginibre,J. «Statisticalensemblesofcomplex,quaternion,andrealmatrices». J.MathematicalPhys.,6(1965),440–449.

[3] Hanin,B. «Correlationsandpairingbetweenzerosandcriticalpointsof Gaussianrandompolynomials». Int.Math.Res.Not.IMRN,2015(2)(2015), 381–421.

[4] Hedenmalm,H.;Lindqvist,P.;Seip,K. «AHilbertspaceofDirichletseries andsystemsofdilatedfunctionsin L2(0, 1)». DukeMath.J.,86(1)(1997), 1–37.

[5] Helson,H. «CompactgroupsandDirichletseries». Ark.Mat.,8(1969), 139–143.

[6] Hough,J.B.;Krishnapur,M.;Peres,Y.;Virág,B. ZerosofGaussiananalyticfunctionsanddeterminantalpointprocesses.Providence:American MathematicalSociety,2009.(UniversityLectureSeries;51)

[7] Kac,M. «Ontheaveragenumberofrealrootsofarandomalgebraic equation». Bull.Amer.Math.Soc.,49(1943),314–320.

[8] Kahane,J.-P. Somerandomseriesoffunctions.2aed.Cambridge:CambridgeUniversityPress,1985.(CambridgeStudiesinAdvancedMathematics;5)

[9] Littlewood,J.E.;Offord,A.C. «Onthedistributionofzerosand a-values ofarandomintegralfunction.II». Ann.ofMath.(2),49(1948),885–952; errata50(1949),990–991.

[10] Mehta,M.L. Randommatrices.3aed.Amsterdam:Elsevier:Academic Press,2004.(PureandAppliedMathematics(Amsterdam);142)

[11] Montgomery,H.L. «Thepaircorrelationofzerosofthezetafunction».A: Analyticnumbertheory (Proc.Sympos.PureMath.,vol. xxiv,St.LouisUniv., St.Louis,Mo.,1972).Providence,RI:Amer.Math.Soc.,1973,181–193.

[12] Odlyzko,A.M. «Onthedistributionofspacingsbetweenzerosofthe zetafunction». Math.Comp.,48(177)(1987),273–308.

[13] Sodin,M. «ZerosofGaussiananalyticfunctions». Math.Res.Lett.,7(4) (2000),371–381.

DepartamentdeMatemàticaAplicadaiAnàlisi UniversitatdeBarcelona

GranVia 585, 08007 Barcelona

BGSMath jortega@ub.edu

ButlletídelaSocietatCatalanadeMatemàtiques Vol.30,núm.2,2015.Pàg.207–209

Englishsummaries

JoaquimBruna

Non-linearapproximationandcompressivesampling

Inthispaperwegiveanintroductiontorelativelynewfieldinmathematics,the socalledcompressedsensingorcompressivesampling.Itcanbepresentedas abranchofsignalanalysis,whoseappearanceisrelatedtoanotherimportant field,bigdataanalyis.Compressedsensingdoesnotdealwithprocessingbig datasets,butratherwithsamplingmethodsthatdonotleadtounnnecessary data.Forthesakeoftheexpositionwebrieflyreferaswelltononlinearapproximationtheory.

Keywords: discretisation,linearapproximation,non-linearapproximation,Hilbertbasis,compressivesampling,sparsevectors,decodificator,randommatrices,non-coherentbases.

MSC2010SubjectClassification: 94A12,68P30,41A46.

PilarGuerreroandTomásAlarcón

Stochasticmultiscalemodelsofcellpopulationdynamics:asymptoticandnumericalmethods

Inthispaperwepresentanewmethodologythatallowsustoformulateand analysestochasticmultiscalemodelsofthedynamicsofcellpopulations.Inthe spiritofexistinghybridmultiscalemodels,wesetupourmodelinahierarchical wayaccordingtothecharacteristictimescalesinvolved,wherethestochastic populationdynamicsisgovernedbythebirthanddeathratesasprescribed

bythecorrespondingintracellularpathways(e.g.stochasticcell-cyclemodel). Thefeed-backloopisclosedbythecouplingbetweenthedynamicsofthe populationandtheintracellulardynamicsviatheconcentrationofoxygen: Cellsconsumeoxygenwhich,inturn,regulatetherateatwhichcellsproceed throughtheircell-cycle.Thecouplingbetweenintracellularandpopulation dynamicsiscarriedoutthroughanovelmethodtoobtainthebirthratefrom thestochasticcell-cyclemodel,basedonamean-firstpassagetimeapproach. Cellproliferationisassumedtobeactivatedwhenoneormoreoftheproteins involvedinthecellcycleregulatorypathwayhitathreshold.Thisviewallowsus tocalculatethebirthrateasafunctionoftheageofthecellandtheextracellular oxygenintermsofthecorrespondingmeanfirstpassagetime.Wethenproceed toformulatethestochasticdynamicsofthepopulationofcellsintermsofan age-structuredMasterEquation.Further,wehavedevelopedgeneralisationsof asymptotic(WKB)methodsforourage-structuredMasterEquationaswellas a τ -leapmethodtosimulatetheevolutionofourage-structuredpopulation. Finally,weillustratethisgeneralmethodologywithaparticularexampleofa cellpopulationwhereprogressionthroughthecell-cycleisregulatedbythe availabilityofoxygen.

Keywords: multiscalemodelling,stochasticmodelling,cancer,cell-cycle.

MSC2010SubjectClassification: 92B05.

TimothyG.MyersandSarahL.Mitchell

Amathematicalanalysisofthemotionofanin-flightsoccerball

Inthispaperananalyticalandnumericalstudyofthethree-dimensionalequationsdescribingthemotionthroughtheairofaspinningballispresented.The initialanalysisinvolvesconstantdragcoefficientsbutislaterextendedtoinvolve dragvaryingwiththespinratio.Excellentagreementisdemonstratedbetween numericalandanalyticalresults.Theanalyticalsolutionshowsexplicitlyhow theballsmotiondependsonparameterssuchasballroughness,velocityand atmosphericconditions.Theimportanceofapplyingthree-dimensionalmodels, ratherthantwo-dimensionalapproximations,isdemonstrated.

Keywords: aerodynamics,soccerballflight,spinningsoccerball,Magnusforce, perturbationsolution.

MSC2010SubjectClassification: 34L30,76G25.

JoaquimOrtega-Cerdà

(Random)powerseries

Theconstructionofrandomfunctionswithinterestingpropertiesisaclassical subjectinMathematics.Lately,therehasbeenarenewedinterestintherandom zerosofpolynomialsandofentirefunctionsspurredinpartbythegrowing literatureonthespectrumofrandommatrices.

Keywords: Randompolynomials,Gaussiananalyticfunctions.

MSC2010SubjectClassification: 30B20,26C10,30C15,15B52.

Instruccionsperalsautors

Elsarticlessotmesosapublicaciós’hand’enviaralseditorsoaqualsevol membredelcomitèeditorial,percorreuelectrònic,preferentmentenformat PDF.Elsoriginalshandecontenirlaversióanglesadeltítol,unresumbreuen catalàienanglès,paraulesclauencatalàienanglèsielscodisdelaclassificació permatèriesMSC2010.

Lesversionsdefinitivesdelsarticlesacceptatss’handepresentarencodiTEX, preferentmentenl’estilLATEXpropidel Butlletí.Aquestestilespotobtenira lespàgineswebdelaSocietatCatalanadeMatemàtiques(SCM).Femnotarque enaquestapublicaciós’utilitzapreferentmentelpuntperaseparardecimals, enllocdelacomarecomanadaperl’IEC,perpoderfacilitarlacomprensióde lesexpressionsmatemàtiques.Pertald’accelerarelprocésdeproducció,es pregaalsautorsquesegueixinlesindicacionscontingudeseneldocument d’exemple.

Laversióenpaperdel Butlletí s’imprimeixenblancinegre.Quanun articlecontinguifiguresencoloriesconsidericonvenient,l’autorproporcionarà unaversiódelsgràficssubstituintelcolorpertonsdegrisosilíniesdegruix variable.Aixímateixmodificaràelscomentarisquefacinreferènciaalcolorde lesfigures.Enqualsevolcasel Butlletí publicaràl’originalencolorenelseu formatelectrònic.

Elsautorsdelsarticlespublicatsal Butlletí enreteneneldretdecòpia (copyright)iautoritzenl’IECadifondre’ls,tantatravésdelapublicacióimpresa commitjançantelsportalsdigitalspropisod’altresambquès’estableixinels convenisoportunsaaquestefecte.Ésresponsabilitatdelsautorsassegurar queesdisposadelsdretsdereproducciódelsgràficsidelesfiguresquehi apareguin.CadaautorrebràunacòpiaenPDFd’altaqualitatdelaversiódigital delseuarticleiunexemplarimprèsdelnúmerodel Butlletí enelquales publiqui.

Lacorrespondènciaadministrativarelacionadaambel Butlletí s’had’adreçaralaSCM.

JuliàCufí(editorencap)

Comitèeditorial

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona jcufi@mat.uab.cat

BartomeuColl

Dep.deMatemàtiquesiInformàtica UniversitatdelesIllesBalears tomeu.coll@uib.cat

NúriaFagella

Dep.deMatemàticaAplicadaiAnàlisi UniversitatdeBarcelona fagella@maia.ub.es

JosepMariaFont

Dep.deProbabilitats,LògicaiEstadística UniversitatdeBarcelona jmfont@ub.edu

ArmengolGasull

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona gasull@mat.uab.cat

GáborLugosi

ICREAiDepartamentd’Economia UniversitatPompeuFabra gabor.lugosi@upf.edu

RosaCamps(editoraadjunta)

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona rcamps@mat.uab.cat

JorgeMateu

DepartamentdeMatemàtiques UniversitatJaumeI mateu@mat.uji.es

MarcNoy

DepartamentdeMatemàticaAplicadaII UniversitatPolitècnicadeCatalunya marc.noy@upc.edu

FrancescPlanas

DepartamentdeMatemàticaAplicadaI UniversitatPolitècnicadeCatalunya francesc.planas@upc.edu

AgustíReventós

DepartamentdeMatemàtiques UniversitatAutònomadeBarcelona agusti@mat.uab.cat

MartaSanz-Solé

Dep.deProbabilitats,LògicaiEstadística UniversitatdeBarcelona marta.sanz@ub.edu

SocietatCatalanadeMatemàtiques

La SocietatCatalanadeMatemàtiques(SCM) ésunasocietatfilialdel’Institutd’EstudisCatalans,quecontinualesactivitatsdelaSecciódeMatemàtiques delaSocietatCatalanadeCiències,quefoufundadaperl’Institutl’any1931. Lesfinalitatsdela SCM són:elconreudelesciènciesmatemàtiques,l’extensió delseuconeixementenlasocietatcatalana,elfomentdelseuensenyament idelasevainvestigacióteòricaiaplicada,aixícomlapublicaciódetotamena detreballsques’adeqüinaaquestsobjectius.La SCM desenvolupalesseves activitatsenlesterresdellenguaiculturacatalanes.Elcatalàés,doncs,la llenguapròpiadela SCM ilaqueésusadanormalmententotselsseusactesi publicacions.

La SCM editalespublicacionsperiòdiques SCM/Notícies i Butlletídela SocietatCatalanadeMatemàtiques.Elssocisdela SCM reben,gratuïtament, aquestesduespublicacions.

La SCM téconvenisdereciprocitatambdiversessocietatsmatemàtiques d’arreudelmón,mitjançantelsqualselssocisdela SCM obtenenunareduccióenlaquotadesocid’aquestessocietats.Aixímateix,elssocisdela SCM podenfer-sesocisdelaSocietatMatemàticaEuropeapagantunaquota complementària.

LaJuntaDirectivadela SCM estàconstituïdaperlespersonessegüents:

President:XavierJarqueiRibera

Vicepresident:EnricVenturaiCapell

Adjuntadelavicepresidència:IolandaGuevaraiCasanova

Secretari:AlbertRuiziCirera

Tresorera:NatàliaCastellanaiVila

Vocals:NúriaFagellaiRabionet,JosepGranéiManlleu,Agustí ReventósiTarrida,CarlesRomeroiChesa,OriolSerraiAlbó,Esther Silberstein,ManelUdinaiAbelló

Delegatdel’IEC:JoanGirbauiBadó

L’adreçadela SCM éscarrerdelCarme,47,08001Barcelona.Telèfon: 933248583.Fax:932701180.Correuelectrònic: scm@iec.cat.Adreçaweb: http://scm.iec.cat.

El Butlletí de la Societat Catalana de Matemàtiques publica, en llengua catalana, exposicions matemàtiques de qualitat, que puguin interessar a un nombre elevat de lectors. Es donarà prioritat a aquells treballs en què destaquin la claredat d’exposició i l’interès general del tema. El Butlletí està obert a tots els camps de la matemàtica i també als aspectes matemàtics de les ciències experimentals, la tecnologia, l’economia, etc., així com a altres àrees, com la història, la didàctica i la filosofia, sempre que els treballs tinguin un component matemàtic important. També tenen cabuda al Butlletí aquells articles que desenvolupin un aspecte significatiu de la problemàtica de la professió matemàtica al nostre país.

El Butlletí publica un volum a l’any, dividit en dos números, que es trameten gratuïtament a tots els socis. El Butlletí es publica també en format electrònic. L’edició electrònica del Butlletí pot obtenir-se des del portal de revistes científiques en línia de l’IEC o al servidor http://scm.iec.cat.

La correspondència administrativa s’ha d’adreçar a la Societat Catalana de Matemàtiques.

Editor en cap

Julià Cufí

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Comitè editorial

Bartomeu Coll

Dep. de Matemàtiques i Informàtica

Universitat de les Illes Balears

Núria Fagella

Dep. de Matemàtica Aplicada i Anàlisi

Universitat de Barcelona

Josep Maria Font

Dep. de Probabilitats, Lògica i Estadística

Universitat de Barcelona

Armengol Gasull

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Gábor Lugosi

ICREA i Departament d’Economia

Universitat Pompeu Fabra

Societat Catalana de Matemàtiques

Carrer del Carme, 47 - 08001 Barcelona tel. 933 248 583 - fax 932 701 180

scm@iec.cat - http://scm.iec.cat

Editora adjunta

Rosa Camps

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Jorge Mateu

Departament de Matemàtiques

Universitat Jaume I

Marc Noy

Departament de Matemàtica Aplicada II

Universitat Politècnica de Catalunya

Francesc Planas

Departament de Matemàtica Aplicada I Universitat Politècnica de Catalunya

Agustí Reventós

Departament de Matemàtiques

Universitat Autònoma de Barcelona

Marta Sanz-Solé

Dep. de Probabilitats, Lògica i Estadística Universitat de Barcelona