Grade 7 • Study Guide Mathematics

Owned and published by Optimi, a division of Optimi Central Services (Pty) Ltd.
7 Impala Avenue, Doringkloof, Centurion, 0157 info@optimi.co.za www.optimi.co.za
© Optimi
Apart from any fair dealing for the purpose of research, criticism or review as permitted in terms of the Copyright Act, no part of this publication may be reproduced, distributed, or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or any information storage and retrieval system without prior written permission from the publisher.
The publisher has no responsibility for the persistence or accuracy of URLs for external or third-party internet websites referred to in this publication, and does not guarantee that any content on such websites is, or will remain, accurate or appropriate.
There are instances where we have been unable to trace or contact the copyright holder. If notified, the publisher will be pleased to rectify any errors or omissions at the earliest opportunity.
Reg. No.: 2011/011959/07

Mathematics
Study guide
Grade 7


*
Level of difficulty
1
Basic knowledge 25%
Level of difficulty 2
Routine procedures 45% **
Assessment analysis
• Use mathematical facts and vocabulary
• Use the correct formulas
• Predict answers and round off values
• Theoretical knowledge
• Complete known procedures
• Apply knowledge and facts with more than one step
• Come to conclusions from given information
***
Level of difficulty 3
Complex procedures 20%
Level of difficulty
4
Problem-solving 10%
Level of difficulty
****
5 ****
Sample
• Basic calculations as learned from examples and exercises
• Complex calculations and high order arguments
• Euclidean Geometry
• No stipulated path to follow
• Similarities and differences between presentations
• Need conceptual and holistic approaches to problems
• Unseen and not-routine problems.
• Problems in different sections
• Still in curriculum and study guide
• Mostly aimed at practical and everyday situations.
• High order of thinking
* Advanced Often regarded as acceleration of the curriculum. Not included in tests and exam papers.
Unit 1: Number systems
Content in this unit:
• Where do number systems come from?
• Natural numbers
• Whole numbers (Counting numbers)
• Integers
• Fractions (Rational numbers)
• Roots and surds (Irrational numbers)
• Properties of number systems (associative, commutative and distributive laws)
Exercise 1: Where do number systems come from?
There is proof that the Ishango people of the Democratic Republic of the Congo (DRC) made marks on bones to count their cattle or family members. The oldest bone found to confirm these assumptions is approximately 20 000 years old. The number system that we use today is the Hindu-Arabic system and it was developed more than 1 000 years ago by Hindu-Arabic mathematicians. The Egyptian number system consists of symbols. Examples of the two number systems are:
1.1* Write down the Egyptian equivalent for the number 3 516
1.2* Write down the Egyptian equivalent for the number 2 182.
1.3*** Write the Hindu-Arabic number for
1.4* Study the number 234 654 365 123 987 341 236 687. Write down the number that is 10 000 more than the given number.
1.5*** Investigate: For fun
Draw the following table in your answer book and translate the terms addition, subtraction, multiplication and division in any other two languages.
Exercise 2: Natural numbers
Natural numbers are the numbers from 1 to infinity. The symbol used is N. If tabulated: N = {1; 2; 3; 4; 5 …}
If we look at all the number systems together, then A in this diagram will represent the natural numbers:
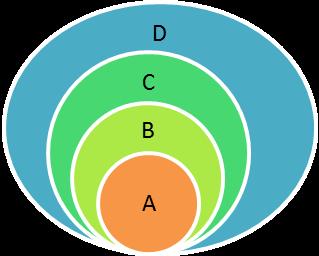
The symbol for natural numbers is N
A represents natural numbers. As the unit progresses, the other number systems will be explained.
Each digit in natural numbers has its own meaning.
Milliard and billion denote the same number Milliard is almost never used in America and Britain, but is often used in Continental Europe.
Decimal system
1 million= 1000 000 = 106
Six zeros
1 billion = 1000 000 000 = 109
Nine zeros
1 trillion =1000 000 000 000 =1012
Twelve zeros
1 quintillion = 1018
Eighteen zeros
thousand million (100 0000)2 (100 0000)3 (1000)2
2.1** Complete the table by identifying the place value of the 7
2.1.1*
2.1.3**
2.1.6* 1233452 7 2.1.7** 34 52 7 825 455
2.1.8* 7 82
2.1.9**** 34 7 84 556 723
2.2** Write the number from the description given.
Example 4 Hundred Thousands 400 000
2.2.1* 6 Tens
2.2.2* 12 Thousands
2.2.3** 876 Millions
2.2.4* 9 Units
2.2.5** 47 Hundreds
2.2.6*** 639 Ten Thousands
2.2.7**** 32 456 Hundreds
2.3*** Add 10 to all the following values. Write your answers in the table.
2.3.1* 65 382
2.3.2* 1 234
2.3.3** 87 592
2.3.4*** 96 795
2.3.5**** 9 328 999
2.4** Complete the table by calculating what is asked
Example 3 761 Add 400 4 161
2.4.1** 676 767 Add 1 million.
2.4.2* 78 493 Subtract 50.
2.4.3** 78 493 Add 9 000.
2.4.4** 12 121 212 Subtract 1 million
2.4.5**** 875 462 867 Add four hundred thousand
2.4.6** 444 444 Add 5 000
2.5** Break down the natural numbers as shown in the example Number Answer Example 1 234
2.5.1* 648
2.5.2* 33 333
2.5.3**** 54 545 454
2.5.4** 5 678
2.5.5* 6
2.5.6** 765 432
2.6** Arrange the following natural numbers from small to big: {2542; 154; 2441; 2523; 2509}.
2.7** Arrange the following natural numbers from big to small: {592; 523; 2600; 2699}.
In Mathematics we use symbols to show greater than or less than. If you look at the following symbols from left to right, you can say:
Example: 234 > 233 345 < 346
2.8** Place a < or > symbol between the values in the table
1 < or
When doing addition and subtraction of natural numbers, your answer must have enough steps to show that you did not use a calculator.
Example
2 379 + 6 666 = 2 379 + 6 666 9 045
Make sure you know where the = sign is placed. Know how and where this sign is placed.
9 370 – 6 666 = 9 379 – 6 666 2 713
Simplify the following. Show your calculations. You are not allowed to use a calculator
2.9* 17 + 25
2.10** Use your answer and write down the correct answer for 17 hundred plus 25 hundred
2.11** Now use your answer and write down the correct answer for 17 million plus 25 million.
2.12**** Determine the sum of 17 Hundred Thousands and 25 Ten Thousands
Calculations with natural numbers can only be one of the following:
Use the prescribed methods and determine the answers of the following You are not allowed to use a calculator
2.13** 2 345 + 999
2.14** 2 345 – 999
2.15** 2 345 x 99
No calculators. Write down all the actual calculations to show that you did not use a calculator.
2.16*** 2 345 ÷ 9 with the long division method.
2.17*** 2 345 ÷ 99 with the long division method.
2.18**** 2 345 ÷ 999 with the long division method.

Rewriting English sentences as mathematical sentences (number sentences) is essential to solving word problems. The following terms for calculations may be used. Study them and use them
Symbols Meaning Other English words × Multiply Product of ÷ Divide Quotient of – Subtract Difference between + Add Sum of
Write the following English sentences in mathematical (number) sentences Simplify them without using a calculator
The remainder is asked for question 2.21. That means that you have to do this question with long division In future we will use decimals, but for now the remainder and quotient are both integers.
2.19** Determine the sum of 12 and 56.
2.20** Calculate the product of 12 and 56.
2.21** What is the quotient if 56 is divided by 12? Give the remainder.
2.22*** A printing company prints 1 436 books per day. How many books did they print in July 2013 if they did not work on Saturdays and Sundays?

2.23**** A yacht sails in one direction. On the first day it sails 275 km and then 35 kilometres further each day. How far will the yacht be from the harbour at the end of the third day?
Day 1= 275 km

Day 2
Day 3
2.24*** Juan drove 1 035 metres to a shop. John drove 2 285 metres to the same shop. How much further did John drive?
2.25 Sandra has to make 34 skirts for girls participating in a school play. She buys 2 rolls of material of 44 metres each. Each skirt requires 3 metres of material.
2.25.1*** Show all your calculations and determine how much material she still needs to buy. You are not allowed to use a calculator.
2.25.2*** To make the skirts, a single piece of 3 metres of material is required. The material can’t be joined. Explain how many rolls of material must be bought and how many metres will remain on each roll after 34 pieces of 3 metres have been cut.
Rounding off natural numbers must be done In Tens, Hundreds and Thousands.
Examples
Rounding off to 10
(It means that the number must be divided by 10 without leaving a remainder.)
Rounding off to 100.
(It means that the number must be divided by 100 without leaving a remainder.)
Rounding off to 1 000
(It means that the number must be divided by 1 000 without leaving a remainder.)
Look at the Units
• When less than 5, round off downwards.
• When 5 or more, round off upwards.
Look at the Tens and Units (last two digits).
• When less than 50, round off downwards.
• When 50 or more, round off upwards
Look at the last three digits (Hundreds, Tens and Units).
• When less than 500, round off downwards.
• When 500 or more, round off upwards.
2.26** Complete the table by rounding off the numbers. Read the headings of the table.
Round off the following numbers to the nearest 5.
Example:
(It means that 5 must be divided into the value without a remainder. Remember, the Units that are a 1 or a 2 must be rounded off downwards and Units that are 3 and 4, upwards.)
• 62 rounded off to the nearest 5 is 60.
• 63 rounded off to the nearest 5 is 65
• 84 rounded off to the nearest 5 is 85
When you round off in Mathematics, the following sign is used:
For clarity, the number you round off to is written at the end of the answer. For examples:
Sample
26 ≈ 30 to the nearest 10
3 456 ≈ 3 500 to the nearest 100
2.27*** Round off 123 456 to the nearest 5
2.28**** Round off 74 to the nearest 7.
2.29*** Shaun buys a pair of trousers for R243 and a jacket for R679.
2.29.1* Round off each to the nearest R10 and give the total amount he paid for the trousers and the jacket.
2.29.2** What will the amount be if Shaun first adds the amounts before rounding off?
2.29.3*** What is the difference between the answers in the previous two questions? Do you think one will always get to the same answers?
Order of operations
When questions are asked that include a combination of adding, subtracting, multiplying or division, it is important to remember the rules regarding the order of operations
Remember there are priorities for + , –, ÷× and
This sequence applies up to Grade 12. Study this now and you will never have to study it again.
The sequence of calculations is as follows:
1. Brackets (…)
2. Exponents.
3. Multiplication and division from left to the right
4. Adding and subtraction from left to the right
Simplify the following by doing only one calculation for each step:
Example 1: 2 + 3 x 4 = 2 + 12 = 14
Sample
Example 2: 23 – (12 + 8) +2 = 23 – 20 + 2 = 3 + 2 = 5
Example 4 2 + 3 10 – 6 + (3 – 2) + of 12 = 2 + 3 10 – 6 + 1 + of 12 = 2 + 3 10 – 6 + 1 + 6 = 2 + 30 – 6 + 1 + 6 = 32 – 6 + 1 + 6
= 26 + 1 + 6
= 27 + 6 = 33
Remember: Once the calculation in the bracket has been completed, the bracket disappears.
Example 3: 30 ÷ 3 x 2 + 15 ÷ 5 = 10 x2 + 15 ÷ 5
= 20 + 15 ÷ 5
= 20 + 3 = 23
Example: 5 2 + 23 2 – of (21 + 3)
= 2 + 23 2 – of 24
= 2 + 8 2 – of 24 = 2 + 8 2 – 8 = 2 + 16 – 8 = 18 – 8 = 10
Simplify the following expression by doing one calculation per step only.
2.30*
2.31* 4 + 2 3 – 1 1 + 3 2 6 – 2
2.32** 9 – (12 – 8)
2.33** 2.34** 3 + 3 3 – 3 (3 + 2) (6 – 2)
2.35** 2 + 2 2 2 – 2 + (2 + 2)
2.36** 8 – 2 3 + 6 – (5 – 1)
2.37** 10 – 4 + (3 – 1) 3
2.38** 0203×+×
2.39** (6 – 2 + 7) + (3 – 2 + 12)
Do one calculation for each step. It will teach you the preference and the use of the = sign. Remember that everything must be identical before and after the = sign.
2.40*** Simplify by doing only one calculation for each step.
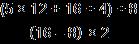
Treat the division line as two large brackets.
• Simplify the numerator on its own and the denominator on its own.
• Then divide the numerator by the denominator. Sample
It is easy to multiply by 0. The answer stays zero.
REMEMBER!
(0)4 = 0 and not 4 6 x 0 = 0 and not 6
Brackets first. A bracket disappears when the answer is written down.
x and ÷ have the same priority. The first sign must be executed first.
Be aware
All the number 2s can be confusing. Work systematically … one calculation for each step.
Factors
This is a general term which means these are numbers that divide exactly into a bigger number, with an integer as an answer. Therefore 10 will be a factor of 20 because 10 can be divided into 20.
Prime factors
A prime number is a number that has exactly two factors, namely the number 1 and the number itself.
This means that only two numbers can be divided into a prime number without a remainder. There are an infinite number of prime numbers, but no formula exits to determine the number of prime numbers.
The set of prime numbers is = {2; 3; 5; 7; 11; 13; 17; 19 …}
The number 1 1 is neither a prime number nor a composite number.
Composite factors
Numbers that can be divided by more than 2 factors are called composite numbers. For example, 24 is composite because it can be divided by 1, 2, 3, 4, 6, 8, 12 and 24. Composite numbers have three or more factors.
Example: Factors of 24 = {1; 2; 3; 4; 6; 8; 12; 24} = {the number 1} + {prime numbers} + {composite numbers} = {1} + {2; 3} + {4; 6; 8; 12; 24}
4 is written as 2 x 2
6 is written as 2 x 3
12 is written as 2 x 2 x 3
24 is written as 2 x 2 x 2 x 2 x 3
2.41* 12
2.42* 30
2.43** 36
2.44** 35
Prime numbers that are multiplied are called composite factors.
Write each number given as sets of 1, prime numbers and composite factors. Use the example given.
SampleFirst determine the prime factors.
The use of the ladder method to determine prime factors.
Example:
360 =2 x 2 x 2 x 3 x 3 x 5
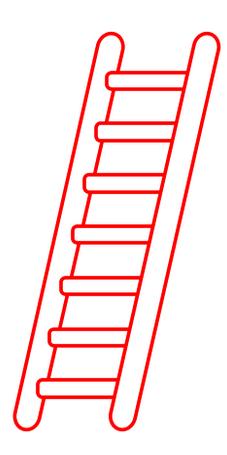
Use the ladder method
Divide the number by the first prime number that can be divided into that number. Continue dividing by the same number until you end up with a remainder. Then use the next prime number.
Prime numbers = {2; 3; 5; 7; 11; 13 ...}
Write the following numbers as the product of their prime numbers. Use the ladder method. This means the same as writing the number as the product of prime factors.
2.50* 24
2.51** 68
2.52* Determine the largest prime number that can be divided into 39 600.
First learn the following:
• Multiples. Numbers into which the given number can be divided.
• Example: multiples of 6 are {6; 12; 18; 24; 30 …}
• Factors. These are numbers that can be divided in the given numbers:
Example: factors of 12 is {1; 2; 3; 4; 6; 12}
Example: Factors of 8 = {1; 2; 4; 8} Multiples of 8 = {8; 16; 24; 32 …}
Determine the multiple and factors of the following:
2.53* 6
2.54* 12
2.55* 18
2.56* 24

Multiples are large numbers. Factors are small numbers.
Use the ladder method.
Determine the LCM (lowest common multiple) and HCF (highest common factor) of two or more integers.
