Stromversorgung ohne Stress – Band 1 booksbooks
Grundlagen und Schaltungen der Stromversorgungstechnik
Für elektronische Geräte aus der Praxis
Franz Peter Zantis
2., überarbeitete und erweiterte Auflage


Grundlagen und Schaltungen der Stromversorgungstechnik
Stromversorgung ohne Stress
Band 1
2. überarbeitete und erweiterte Version
● © 2026: Elektor Verlag GmbH, Aachen.
2., überarbeitete und erweiterte Auflage
● Alle Rechte vorbehalten.
Die in diesem Buch veröffentlichten Beiträge, insbesondere alle Aufsätze und Artikel sowie alle Entwürfe, Pläne, Zeichnungen und Illustrationen sind urheberrechtlich geschützt. Ihre auch auszugsweise Vervielfältigung und Verbreitung ist grundsätzlich nur mit vorheriger schriftlicher Zustimmung des Herausgebers gestattet.
Die Informationen im vorliegenden Buch werden ohne Rücksicht auf einen eventuellen Patentschutz veröffentlicht.
Die in diesem Buch erwähnten Soft- und Hardwarebezeichnungen können auch dann eingetragene Warenzeichen sein, wenn darauf nicht besonders hingewiesen wird. Sie gehören dem jeweiligen Warenzeicheninhaber und unterliegen gesetzlichen Bestimmungen.
Bei der Zusammenstellung von Texten und Abbildungen wurde mit größter Sorgfalt vorgegangen. Trotzdem können Fehler nicht vollständig ausgeschlossen werden. Verlag, Herausgeber und Autor können für fehlerhafte Angaben und deren Folgen weder eine juristische Verantwortung noch irgendeine Haftung übernehmen.
Für die Mitteilung eventueller Fehler sind Verlag und Autor dankbar.
● Erklärung
Autor und der Verlag haben ihr Bestes getan, um die Richtigkeit der in diesem Buch enthaltenen Informationen sicherzustellen. Sie übernehmen keine Haftung und lehnen hiermit jegliche Verantwortung gegenüber Dritten für Verluste oder Schäden ab, die durch Fehler oder Auslassungen in diesem Buch verursacht wurden, unabhängig davon, ob diese Fehler oder Auslassungen aus Fahrlässigkeit oder aus anderen Gründen resultieren..
● ISBN 978-3-89576-706-7 Print ISBN 978-3-89576-707-4 eBook
● Satz und Aufmachung: D-Vision, Julian van den Berg | Oss (NL)
Druck: Ipskamp Printing, Enschede (NL)
Elektor Verlag GmbH, Aachen www.elektor.de
Elektor ist die weltweit wichtigste Quelle für technische Informationen und Elektronik-Produkte für Maker, Ingenieure und Elektronik-Entwickler und für Firmen, die diese Fachleute beschäftigen. Das internationale Team von Elektor entwickelt Tag für Tag hochwertige Inhalte für Entwickler und DIY-Elektroniker, die über verschiedene Medien (Magazine, Videos, digitale Medien sowie Social Media) in zahlreichen Sprachen verbreitet werden. www.elektor.de
2.1.1.3
2.1.1.4
2.1.1.5
2.1.1.6
2.1.2
2.1.2.1
2.1.2.2
2.1.3.1
2.1.3.2
2.1.3.3
2.1.3.7
2.1.3.8
2.1.3.9
2.1.3.10
2.1.3.11
2.1.4.3
2.1.4.4
2.1.5
3.1.1.2.2
3.1.1.2.3
3.1.1.2.4
3.1.2.1
3.1.2.2
3.1.2.3
3.2
3.3.1
3.3.2
3.3.3
5.1.2.1
5.2.1
5.2.2
5.2.2.1
6.3
8.1.2.3
8.1.2.4
8.2.2.1
8.2.5.1
8.2.5.2
8.2.5.3
8.2.6.2
8.3
Vorwort
Elektronische Schaltungen werden immer weiter integriert. Die Anzahl der Bauelemente reduziert sich ständig. Was bleibt, sind hochintegrierte, komplexe Chips, ein Gehäuse mit Bedienelementen und … die Stromversorgung. Diese spielt für die Funktion eines Gerätes eine fundamentale Rolle. Im Chip können verschiedene Bereiche ausfallen – was noch nicht zum Totalausfall des Gerätes führen muss. Fällt aber die Stromversorgung aus, dann geht gar nichts mehr. Ein Grund, dieser Baugruppe besondere Aufmerksamkeit zu widmen.
Noch etwas darf nicht vergessen werden: in der Stromversorgungsbaugruppe wird die Gesamtaufnahmeleistung des Gerätes umgesetzt. Dies führt zu hohen Temperaturen und Verschließ. Die Stromversorgung ist somit die anfälligste Baugruppe in einem Gerät. Bei den Ausfallstatistiken fällt auf, dass der weitaus größte Fehleranteil in der Stromversorgung, also dem Netzteil oder bei Batteriegeräten in der Batterie-Stromzuführung zu finden ist. Bei defekten Rundfunkempfängern mit IC-Bestückung liegt die Fehlerursache in 44,3 % aller Fälle in der Stromversorgungseinheit [1]. Mehr als genug Gründe also, Netzteilen eine besondere Beachtung zu schenken.
Mathematik kann in der Technik eine große Hilfe sein. In diesem Buch geht es aber mehr um das Verständnis der physikalischen Zusammenhänge. Die Mathematik soll tatsächlich zur ein Hilfsmittel sein.
Zum Schluss sei noch erwähnt, dass dieses Buch das Thema natürlich nicht bis ins letzte Detail behandeln kann. Hinweise zum Platinendesign für Netzteile finden sich im Literaturverzeichnis unter Punkt [23]. Vorschläge zur Optimierung des Schaltverhaltens von Transistoren sind unter [22] beschrieben.
Der Autor
Vorwort zur zweiten Auflage
Vorwort zur zweiten Auflage
Nach dem erscheinen der Bände III und IV der Reihe "Stromversorgung ohne Stress" erhielt ich zahlreiche Anfragen von Lesern, ob bzw. wann der Band I wieder in Buchform verfügbar wäre. Ich war deshalb hocherfreut über die Zustimmung des Verlags zur Herausgabe einer zweiten Auflage.
Bei der Überarbeitung zur Erstellung der zweiten Auflage konnte ich viele Korrekturen vornehmen und einige Ergänzungen einpflegen. Das Grundkonzept ist aber unverändert. Es geht um Stromversorgung für elektrische Geräte – ob als Baugruppe oder als Laborgerät. Ziel ist eine praktische verwendbare Einführung in das Thema. Die Teilbereiche werden dann in Folgebändern ausführlicher behandelt. Zielgruppe sind die "Macher" – die an tatsächlichen, praktisch nutzbaren Ergebnissen interessiert sind.
Das Erscheinen dieser zweiten Auflage ist für mich eine große Freude und Erleichterung.
Alsdorf, im Juni 2025
Franz Peter Zantis


Stromversorgungs-Baugruppen


Stromversorgung für Labor und Service
Kapitel 1 • Quellen
1.1 Spannungsquellen
Die ideale Spannungsquelle gibt - unabhängig von der Belastung - eine konstante Spannung ab. Tatsächlich nimmt die Spannung einer realen Quelle aber mit steigendem Belastungsstrom ab. Dieses Verhalten lässt sich durch Einführung eines Quellen-Innenwiderstandes Ri, der in Serie zu einer idealen Spannungsquelle mit der eingeprägten Spannung U0 geschaltet ist, berücksichtigen. So entsteht die im Bild 1.1 gezeigte Ersatzschaltung für die reale Spannungsquelle. Bei der idealen Spannungsquelle hat der Innenwiderstand den Wert 0 (Ri 0). Im Bild 1.1 befindet sich die eigentliche Quelle im gestrichelten Kasten. Sie besteht aus der Konstantspannung U0 und dem Innenwiderstand Ri der sich im besten Fall wie ein konstanter ohmscher Widerstand verhält.
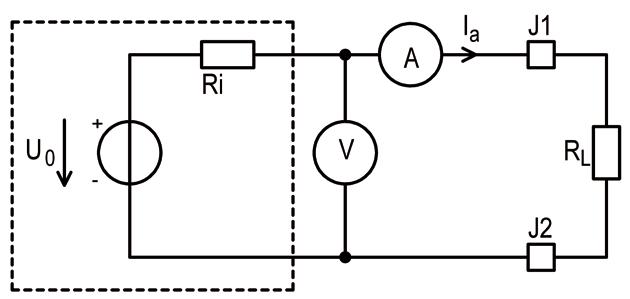
Bild 1.1: Ersatzschaltung einer realen Spannungsquelle bestehend aus idealer Spannungsquelle mit Innenwiderstand Ri. Hier mit angeschlossenem Lastwiderstand RL sowie Spannungs- und Strommesser.
Unter dieser Bedingung nimmt die Ausgangspannung der Spannungsquelle mit steigendem Belastungsstrom I linear ab, da dann der Spannungsabfall am Innenwiderstand Ri steigt. Im Bild 1.2 ist der Funktionsverlauf schematisch dargestellt. Er kann mit Hilfe der allgemeinen Geradengleichung aus der Mathematik (lineare Funktion; Polynom erster Ordnung)
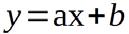
{Gleichung 1.1}
beschrieben werden. Gesucht ist die Ausgangsspannung bei einem bestimmten Ausgangsstrom. Deshalb wird in der obigen Formel y durch Ua ersetzt und x durch Ia. Der Schnittpunkt mit der Ordinate ist U0. Dann ist der Ausgangsstrom 0 und die Spannungsquelle ist unbelastet. Die Größe U0 entspricht dem Absolutglied b der Geradengleichung. Die Kennlinie hat eine negative Steigung a, denn mit zunehmender Belastung sinkt die Ausgangsspannung bis zum Schnittpunkt mit der Abszissenachse ab. Dieser Schnittpunkt wird Ik bezeichnet. Dabei handelt es sich um den Kurzschlussstrom der Quelle. Der Absolutbetrag der Geradensteigung |a| ist gleich dem Quelleninnenwiderstand Ri. Alle drei Größen (U0, Ik und Ri) sind charakteristische Größen einer Spannungsquelle. Für die Gleichung der Funktion Ua = f(I) kann man also schreiben:
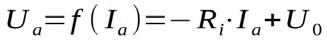
bzw. schöner und aufgrund des Kommutativgesetzes erlaubt:
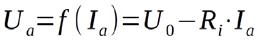
{Gleichung 1.2}
Bild 1.3 zeigt den qualitativen Verlauf für Ua = f(Ia). Das aus der Mathematik bekannte Verfahren zur Berechnung der linearen Funktion aus zwei Punkten lässt sich nun zur Ermittlung des Kennlinienverlaufs der Spannungsquelle anwenden. Dazu müssen für zwei unterschiedliche Belastungsfälle die Werte von Spannung und Strom ermittelt werden.

Bild 1.2: Handelsüblicher 9-V-Akku (NiMH) und zwei Belastungswiderstände. Die Anschlüsse gehen zum Voltmeter.
Als Anwendungsbeispiel soll ein 9-V-NiMH-Akku als Spannungsquelle dienen (Bild 1.2).
Bei Belastung mit einem Widerstand von R1 = 150 gibt der Akku eine Spannung von U1 = 8,9 V ab. Wird der Widerstand auf R2 = 47 geändert, stellt sich eine Spannung von U2 = 8,6 V ein. Die zugehörigen Ströme sind:
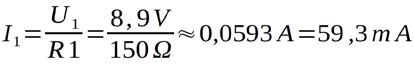
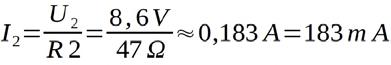
Damit können die beiden Punkte der Geraden angegeben werden:
P1 = (8,9V; 59,3mA) P2 = (8,6V; 183mA)
Für (bzw. Ri) erhält man dann:
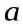
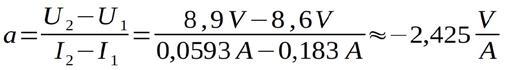
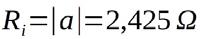
zur Berechnung von b bzw. U0 kann wahlweise P1 als auch P2 herangezogen werden. Hier mal unter verwendung von P1:
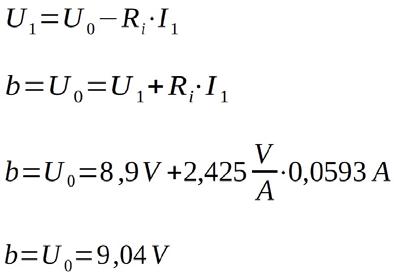
Die Kennlinie Ua = f(Ia) des Akkumulators verläuft also nach der Funktion:
a = f(Ia) = -2,425 V/A ∙ Ia + 9.04 V
oder schöner:
a = f(Ia) = 9.04V- 2,425 Ω ∙ Ia {Gleichung 1.3}
In der Praxis wird man, der Einfachheit halber, zunächst die Spannung der unbelasteten Quelle messen. Dann ist der erste Punkt immer
P1 = (U0; 0)
Dabei wird bei der Messung vorausgesetzt, dass die Belastung durch das Messgerät vernachlässigbar klein ist. In diesem Fall wird lediglich ein tatsächlicher Belastungspunkt benötigt.
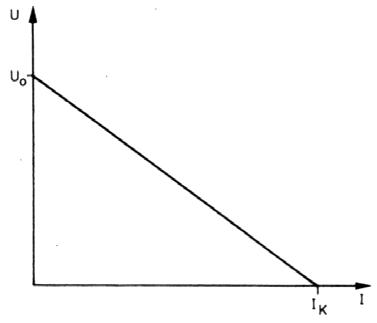
Bild 1.3: Kennlinie einer realen Spannungsquelle U = f(I).
Das ist die Theorie. Leider verhält sich der Innenwiderstand Ri in der Praxis nicht zwangsläufig wie ein konstanter ohmscher Widerstand. Er ist nur im Idealfall konstant. Je nach Quelle kann er um einen Lastpunkt herum (mehr oder weniger großzügig) als konstant angenommen werden. Quellen mit stark variierendem Innenwiderstand heißen nichtlineare Quellen. Ihre Kennlinie weicht von der Idealform der Geradengleichung signifikant ab.
Bei Akkumulatoren zum Beispiel ändert sich der Innenwiderstand mit dem Ladezustand und mit dem Alter der Zelle und auch mit dem aktuellen Belastungsfall und der Temperatur.
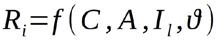
C : Ladezustand in Amperestunden (Ah)
A : Alter (zum Beispiel in Jahren)
Il : Entladestrom in Ampere (A) : Temperatur in °C
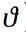
Besonders niedrig ist der Innenwiderstand bei einem neuen Akkumulator ( A = 0 ) der gerade vollständig aufgeladen ist ( C = max.) und nur mit geringer Last beaufschlagt wird ( Il << IK ) bei über Zimmertemperatur.
Zum Beispiel ist bei Solarzellen die Nichtlinearität infolge von Halbleitereffekten beträchtlich. Je stärker der Lichteinfall, umso kleiner ist der Innenwiderstand. Weiterhin hängt der Innenwiderstand vom entnommenen Strom ab und natürlich von der Temperatur. In solchen Fällen kann (wenn denn wirklich Bedarf besteht) für die betreffende nichtlineare Quelle nur eine eigene, spezifische Beschreibung angegeben werden. Es wird dann in der Gleichung 1.2 anstelle des konstanten Widerstandes Ri die Funktionsgleichung Ri = f(Ia) eingesetzt, die wiederum abhängig ist von Funktion und Aufbau der Spannungsquelle. Die Aufstellung der Funktionsgleichung ist ziemlich aufwändig.
Ich habe beispielhaft den Innenwiderstand einer kleinen Solarzelle aus einem EnergyHarvesting-Projekt [12] vermessen. Dabei habe ich die Beleuchtungsstärke konstant gehalten und die Funktiongleichung Ri = f(Ia) in mühsamer Kleinarbeit aufgenommen. Das geht indem um jeden Belastungspunkt herum zwei Messungen gemacht werden die sich im Laststrom geringfügig unterscheiden. Es ergeben sich für jeden Lastpunkt zwei Ströme und zwei Spannungen aus denen der Innenwiderstand berechnet wird. Alle so ermittelten Innenwiderstände ergeben über den Laststrom aufgetragen die Kennlinie - im Beispiel ergab sich Bild 1.4. Zum Schluss habe ich mit einer Regressionsrechnung die Funktionsgleichung als zugeschnittene Größengleichung aufgestellt:
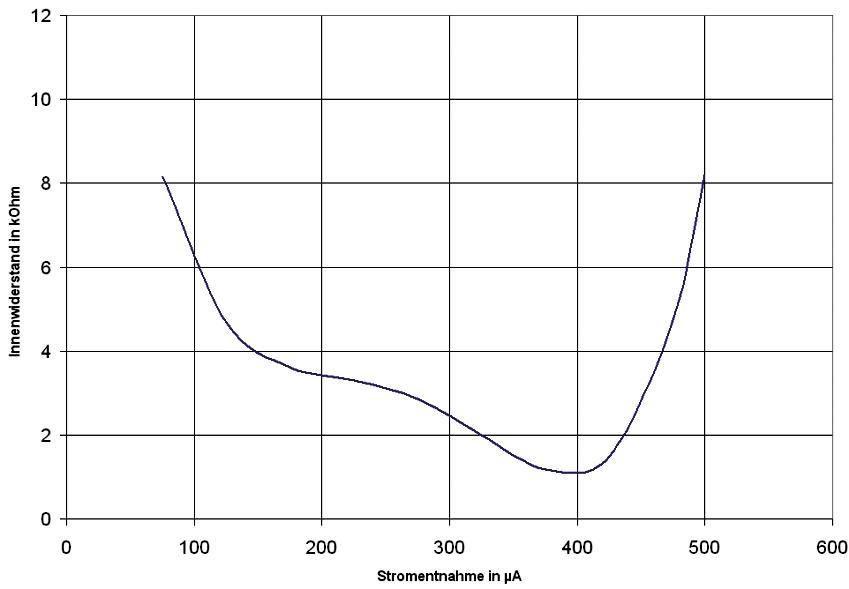
Bild 1.4:Verlauf des Innenwiderstands einer Solarzelle in Abhängigkeit vom entnommenen Strom.
1.1.1 Belastete Spannungsquelle in der Praxis
Sonderfälle wie im Bild 1.4 lasse ich nun mal außer acht. Gute technische Spannungsquellen können in der Umgebung des Arbeitspunktes mit Geraden beschrieben werden. Welche Spannung die Quelle bei einem bestimmten Belastungswiderstand RL abgibt kann dann ermittelt werden, wenn die Widerstandsgerade mit in das Kennlinienfeld der Spannungsquelle eingezeichnet wird. Als Grundlage kann man die Funktionsgleichung Ri = f(Ia) zum Beispiel in ein Tabellenkalkulationsprogramm eintragen, daraus ein Diagramm erstellen und dieses ausdrucken. Alternativ kann das im Abschnitt 1.1.4 beschriebene Programm genutzt werden. Der Schnittpunkt der Quelle mit der Widerstandsgeraden ist der Arbeitspunkt der sich einstellt. Das funktioniert sowohl mit linearen (Bild 1.5) als auch mit nichtlinearen Belastungswiderständen.
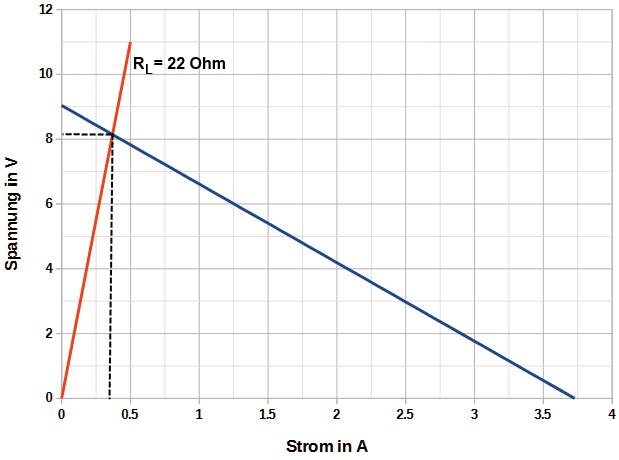
Bild 1.5: Die behandelte, idealisierte Spannungsquelle (9-V-NiMH-Akku) belastet mit einem Widerstand von 22 Ω. Der Schnittpunkt der beiden Geraden ergibt den Arbeitspunkt. Im Beispiel beträgt die Ausgangsspannung 8,14 V und es fließt ein Strom von 0,37 A.
Der Schnittpunkt kann auch rechnerisch ermittelt werden. Für die Spannung Ua im Arbeitspunkt (Schnittpunkt) bei Belastung mit einem ohmschen Widerstand (lineare Last) gilt:
Ua = U0 - Ri ∙ I es gilt aber auch Ua = RL ∙ I
Jetzt werden die Ausdrücke gleichgesetzt und nach I aufgelöst:
U0 - Ri ∙ I = RL ∙ I U0 = I ∙ ( RL + Ri)
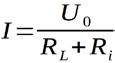
{Gleichung 1.4}
Ist der Strom bekannt, kann zur Berechnung der zugehörigen Spannung sowohl die Gleichung für die Spannungsquellen-Kennlinie als auch für die Widerstands-Kennlinie verwendet werden. Wird die im Beispiel angegebene Spannungsquelle mit einem 22 Ω-Widerstand belastet, ergibt sich damit für den Strom ein Wert von und eine Spannung von
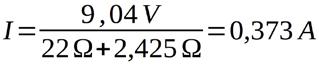
Die Werte stimmen mit denen aus Bild 1.5 überein.
In den Shacks der Funkamateure und in den Werkstätten der Elektroniker sind Widerstände mit bekanntem Widerstandswert zahlreich verfügbar. Für den Praktiker noch interessanter ist deshalb oftmals der Zusammenhang Ua = f(RL). Mit Hilfe von {1.4} gelingt es:
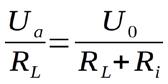
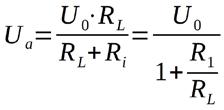
{Gleichung 1.5}
Im Bild 1.6 wurde die Spannungsquelle mit einer Glühlampe belastet. Dabei handelt es sich um eine gewöhnliche Auto-Glühlampe (U=12 V; P=18 W). Glühlampen sind Kaltleiter - also nichtlineare Widerstände, die sich in der Elektronik vielfach hilfreich einsetzen lassen - nicht nur zur Beleuchtung!
Das Problem hier ist, dass die Kennlinie der Glühlampe zunächst unbekannt ist. Allgemeingültig ist aber, dass sich die Kennlinie von Glühlampen gut mit einer Parabel beschreiben lässt. Dazu ist aber eine Beschränkung des Gültigkeitsbereiches (Wertebereich für die unabhängige Variable) erforderlich. Benötigt werden drei Punkte der Kennlinie die durch Messung ermittelt werden. Daraus lassen sich dann die Parameter a, b und c der allgemeinen Parabelgleichung
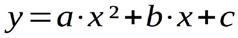
für uns Elektroniker natürlich
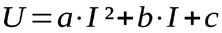
berechnen. Zwei Punkte sind bekannt. Wenn keine Spannung anliegt fließt auch kein Strom: P1(0; 0). Bei Nennleistung liegt die Nennspannung an und es fließt der Nennstrom: P2(12; 1,5). Es reicht also eine Messung. Beim Anlegen einer Spannung von 6 V ergab sich ein Stromfluss von 814 mA: P3(6; 0,814). Nun ist es möglich ein Gleichungssystem aufzustellen mit drei Unbekannten:
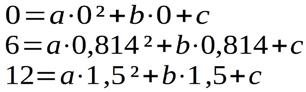
Aus der ersten Gleichung geht hervor: 0 = 0 + 0 + c also ist c = 0.
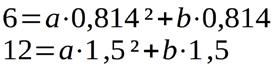
Ich erweitere die erste Gleichung mit 1,5/0,814 und ziehe die beiden Gleichungen voneinander ab:
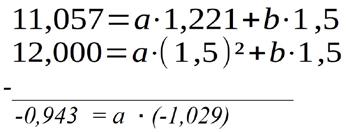
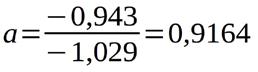
Damit ergibt sich a zu .... und die Gleichung für die Lampe mit IL in A und UL in V. Diese Gleichung gilt für den Definitionsbereich 0 A
Bild 1.6 zeigt graphisch die Lösung.
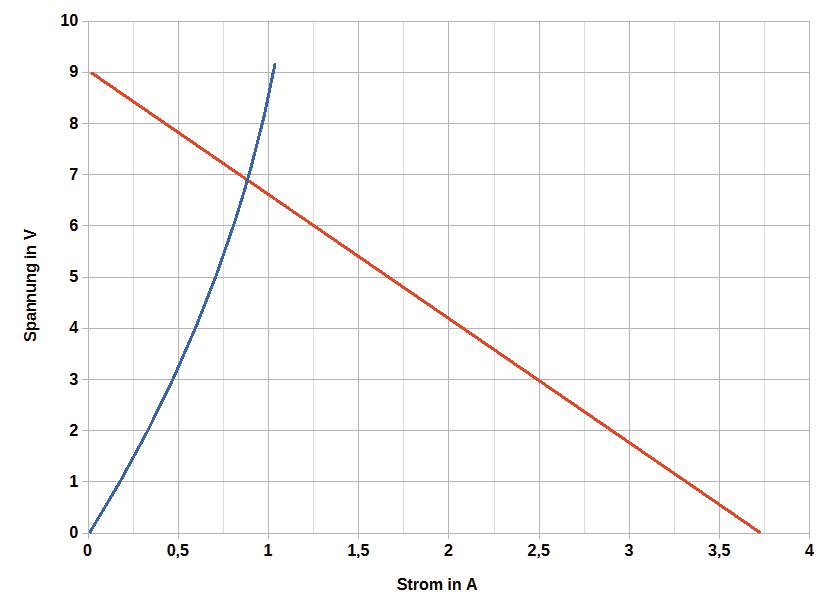
Bild 1.6: Die behandelte Spannungsquelle (9-V-NiMH-Akku) belastet mit einem nichtlinearen Widerstand (Glühlampe 12 V / 18 W). Auch hier wird durch den Schnittpunkt der Kennlinien der sich einstellende Arbeitspunkt bestimmt.
Welche Spannung gibt die Spannungsquelle nun ab, wenn diese Glühlampe angeschlossen wird? Im sich einstellenden Arbeitspunkt sind Strom und Spannung der beteiligten Komponenten gleich. Deshalb kann man also schreiben
IL ist der Ausgangsstrom in A
Es ist offensichtlich eine quadratische Gleichung. Diese kann nun auf die quadratische Normalform zurückgeführt werden (die Einheit lasse ich weg):
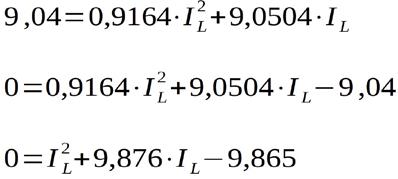
Mit der Lösungsformel für quadratische Gleichungen (z.B. die pq-Formel aus [3]) ergeben sich erwartungsgemäß zwei Lösungen:
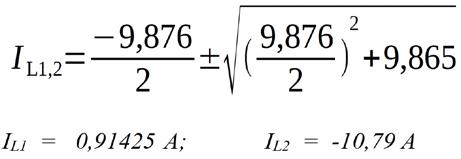
Die Einheit habe ich wieder hinzugefügt. Aus der Kenntnis der technischen Zusammenhänge macht das zweite Ergebnis im vorliegenden Fall keinen Sinn, denn ein negativer Strom würde bedeuten, dass die Glühlampe einspeist - was nicht sein kann. Das erste Ergebnis stimmt mit dem Wert aus Bild 1.6 überein. Die zugehörige Spannung, die sich einstellt, erhält man durch Einsetzen des Stoms in die Spannungsquellengleichung {1.3}:
Auch dieser Wert stimmt mit dem Bild 1.6 überein.
1.1.2 Leistungsabgabe einer Spannungsquelle
Von Interesse ist die Leistung Pa, die eine Spannungsquelle an einem Belastungswiderstand Ra abgibt. Also die Funktion:
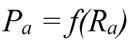
Dabei ist der Arbeitspunkt, bei dem die Leistungsabgabe der Quelle maximal ist, von besonderem Interesse. Die Lösung gelingt mit Hilfe der Kurvendiskussion bzw. der Suche nach Extremwerten.
Wie in den vorherigen Abschnitten bereits dargestellt, ist der Innenwiderstand Ri bei praktisch ausgeführten Spannungsquellen nicht gleich Null. Der Innenwiderstand Ri ist größer als Null, was bei Belastung zum Spannungsabfall an den Anschlussklemmen führt. Dadurch reduziert sich die abgegebene Ausgangsleistung (Bild 1.7). Für die von der Quelle abgegebene Leistung Pa gelten die bekannten Formeln:
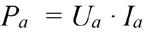
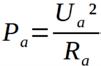
{Gleichung 1.6}
{Gleichung 1.7}
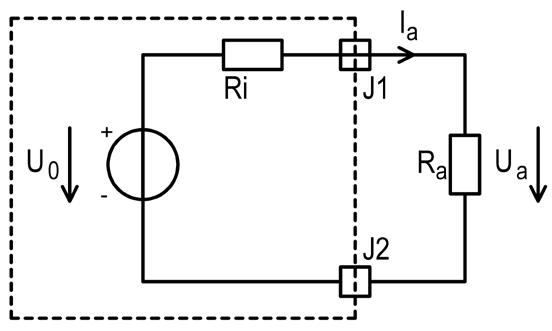
Bild 1.7: Ersatzschaltbild einer technischen Spannungsquelle mit angeschlossenem Lastwiderstand Ra.
Die von der Quelle abgegebene Leistung ist im Leerlauf (Ra = ) gleich Null, da dann zwar die gesamte Quellenspannung U0 an den Klemmen ansteht, aber kein Ausgangsstrom fließt. Auch die Leistung, die in der Quelle vom Innenwiderstand Ri in Wärme umgesetzt wird ist in diesem Falle gleich Null. Es gilt demnach für den Leerlauffall:
Im Kurzschlussfall (Ra = 0) ist die abgegebene Ausgangsleistung Pa ebenfalls gleich Null, da zwar ein hoher Ausgangsstrom (Kurzschlussstrom Ik) fliesst, die Ausgangsspannung aber wegen des Kurzschlusses gleich Null ist. Die Leistung, die vom Innenwiderstand der Quelle in Wärme umgesetzt wird beträgt in diesem Fall aber: oder
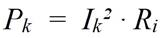
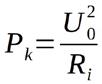
Dabei ist Pk die Kurzschlussleistung, U0 die Leerlaufspannung und Ik der Kurzschlussstrom. Die Kurzschlussleistung ist die höchste, von der Quelle umsetzbare Leistung. Diese Leistung tritt als reine (unerwünschte) Wärme in Erscheinung, die in der Spannungsquelle selbst auftritt. Es gilt demnach für den Kurzschlussfall:
Im Bereich zwischen Leerlauf und Kurzschluss gibt die Quelle aber Leistung ab. Die Höhe der abgegebenen Leistung hängt dabei vom Verhältnis zwischen Innenwiderstand und Last ab. Für den Anwender ist es nun besonders interessant, zu wissen, bei welcher Belastung die Ausgangsleistung ihr Maximum erreicht.
Vor der Suche nach dem Extremum muss die Funktionsgleichung bekannt sein. Für die Ausgangsleistung Pa gilt in jedem Fall:
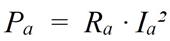
Für den Strom Ia kann angesetzt werden:
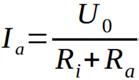
Einsetzen in die Gleichung für die Ausgangsleistung liefert:
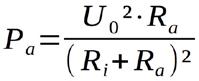
Das Bild 1.8 gibt einen qualitativen Überblick über den zugehörigen Verlauf des Funktionsgraphen. Es ist zu erkennen, dass im Kurzschlussfall die Ausgangsleistung gleich Null ist. Im Leerlauf (Ra = ) ist ebenfalls die Ausgangsleistung gleich Null.
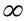
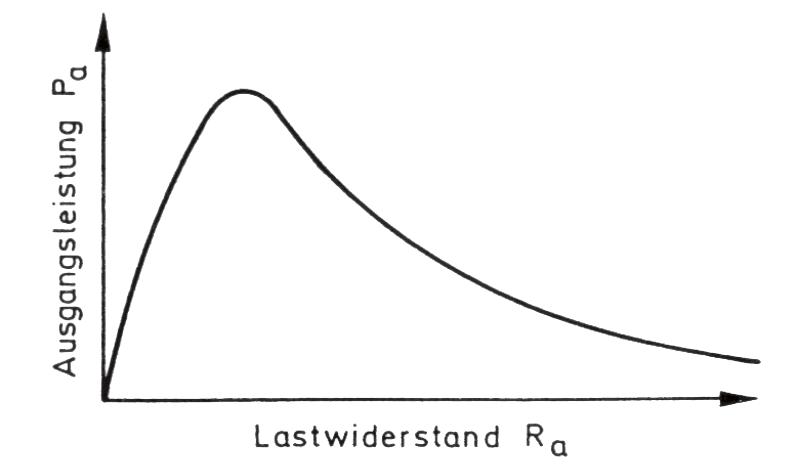
Bild 1.8: Qualitativer Verlauf der Funktion Pa = f(Ra).
Die Kurve nähert sich in diesem Fall asymptotisch der Abszissenachse. Der Schnittpunkt mit der Abszissenachse ist deshalb nicht zu sehen. Allerdings erkennt man wie der Funktionsgraph allmählich auf die Abszissenachse zuläuft und die Ausgangsleistung schnell sehr kleine, für die Praxis unbedeutende Werte annimmt. Für den Gültigkeitsbereich (Definitionsbereich) der Gleichung gilt:
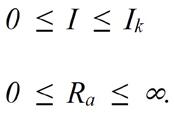
Um den Lastwiderstand Ra zu ermitteln, bei dem die Ausgangsleistung maximal wird ist die Ableitung dPa/dRa zu bilden. Die Funktion Pa = f(Ra) ist eine gebrochen rationale Funktion. Ra kommt sowohl im Zähler als auch im Nenner vor. Deshalb muss die Quotientenregel angewendet werden (siehe dazu auch [4]). Ausgangspunkt ist folgende Gleichung:
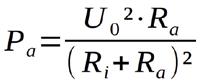
Durch Anwendung der Quotientenregel wird daraus: mit
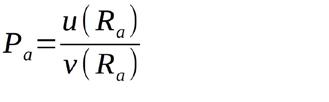
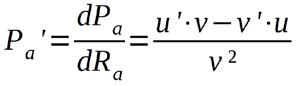
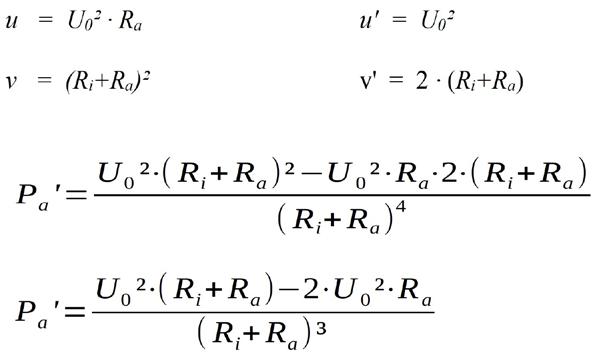
Für die zweite Ableitung, die bei Vorliegen eines Maximums im gesamten Definitionsbereich kleiner als Null sein muss, hilft ebenfalls die Quotientenregel weiter:
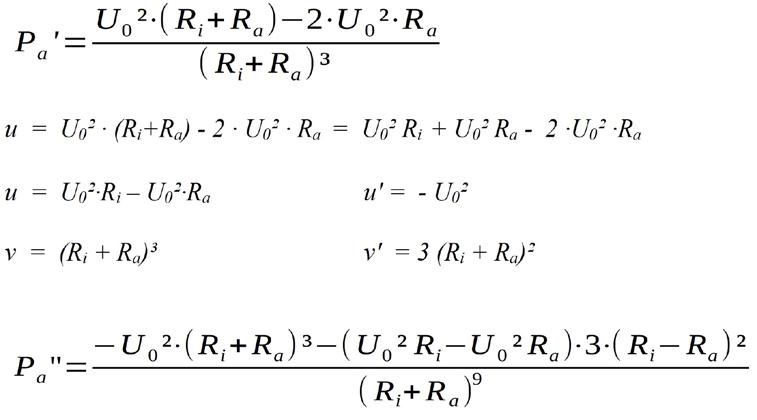
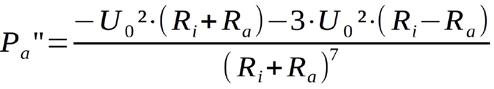
Auf den ersten Blick ist nicht zu erkennen, ob die Gleichung im gesamten Definitionsbereich negative Werte liefert. Es ist eine Abschätzung notwendig. Kritisch ist der Term
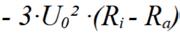
denn für Ra > Ri wird der Ausdruck positiv. Es ist zu untersuchen, ob der in jedem Falle negative Wert des Terms im Definitionsbereich kompensiert werden kann. Mit Sicherheit kann gesagt werden, dass die Bedingung (negative Werte bei der zweiten Ableitung) für Ra ≤ Ri erfüllt ist. Die zweite Bedingung ist erfüllt, wenn gilt:
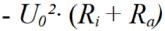
- U0²∙(Ri+Ra) - 3∙U0² ∙ ( Ri-Ra) < 0 bzw.
- ( Ri + Ra) - 3∙(Ri - Ra) < 0
Das Auflösen der Klammern ergibt: - 4∙Ri + 2∙Ra < 0 - 2∙Ri + Ra < 0
-
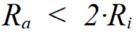
Nur unter dieser Voraussetzung handelt es sich bei dem gesuchten Extremwert eindeutig um ein Maximum.
Die erste Ableitung kann nun gleich Null gesetzt werden:
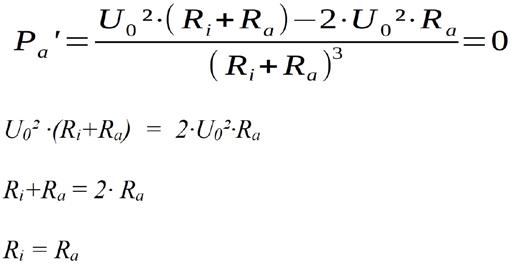
Die Spannungsquelle gibt ihre maximale Leistung ab, wenn der Lastwiderstand Ra gleich groß ist wie der Innenwiderstand Ri. Die abgebbare Maximalleistung läßt sich wie folgt berechnen:
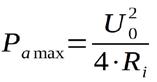
{Gleichung 1.8}
1.1.3 Wirkungsgrad einer Spannungsquelle
Für den Betriebsfall der maximalen Leistungsabgabe beträgt der Wirkungsgrad 50%. Interessanterweise ist dies nicht der maximale Wirkungsgrad. Vielmehr steigt der Wirkungsgrad der Spannungsquelle mit abnehmender Belastung an. Es gilt allgemein:
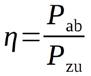
{Gleichung 1.9}
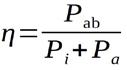
und speziell in diesem Falle: mit und sowie
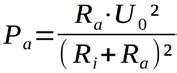
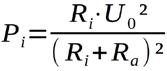
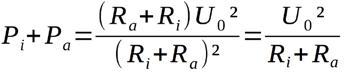
ergibt sich als Resultat: ... oder auch schön:
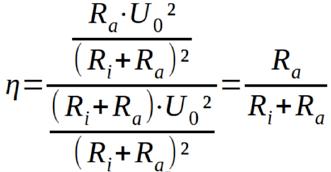
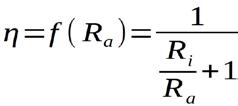
{Gleichung 1.10}
Einen Überblick über den qualitativen Funktionsverlauf des Wirkungsgrades erhält man im Bild 1.9 rechts.
1.1.4 Spannungsquellen-Programm
Zum Abschluss dieses Kapitels ein kleines Programmlisting. Es berechnet aus zwei eingegebenen Lastpunkten die Funktionsverläufe
U = f(I)
Pa = f(Ra) sowie
η = f(I)
einer technischen Spannungsquelle und zeigt diese graphisch am Bildschirm. Beim Bild 1.9 handelt es sich um einen Bildschirmausdruck, der die Bildschirmoberfläche des Programms wiedergibt. Die Menüpunkte fehlen. Für den Ausdruck wurden die folgenden Arbeitspunktdaten beispielhaft eingegeben:
1. U = 12 V, Ra = 1 MΩ (nur mit dem Eingangswiderstand des Messgerätes belastet)
2. U = 9 V, Ra = 15 Ω
Das Programm ist in VB.NET geschrieben und selbsterklärend, so dass sich eine genaue Beschreibung an dieser Stelle erübrigt.
Stichwortverzeichnis
Stromversorgung ohne Stress – Band 1 Grundlagen und Schaltungen der Stromversorgungstechnik
Für elektronische Geräte aus der Praxis
Eines haben alle elektronischen Schaltungen und Geräte gemeinsam: Ihre Funktion hängt von der Stromversorgung ab. Deshalb muss dieser Baugruppe besondere Aufmerksamkeit gewidmet werden. Dieses Buch beinhaltet Grundlagen und Schaltungen der Stromversorgungstechnik für elektronische Geräte aus der Praxis.
Dem aktuellen Trend folgend behandelt der Autor insbesondere die mobile Stromversorgungstechnik sowie die Schaltnetzteiltechnik. Dabei wird berücksichtigt, dass Stromkonstanter gegenüber Spannungskonstantern zunehmend an Bedeutung gewinnen.
Im Buch finden sich die notwendigen Grundlagen zum Bau eigener Stromversorgungsgeräte und -baugruppen. Außerdem enthält es ganz praktische Anwendungsbeispiele, z. B. für den Ersatz defekter Netztransformatoren, für die mobile Stromversorgung auf Fahrradtouren oder für den Betrieb von LEDs.
Diese zweite Auflage wurde gründlich überarbeitet, Fehler wurden behoben und einige Ergänzungen vorgenommen. Der Autor Franz Peter Zantis ist Energieanlagenelektroniker und Ingenieur der Nachrichtentechnik. In einem Forschungsprojekt hat er sich ausführlich mit der Stromversorgung eigensicherer Geräte auseinandergesetzt und zahlreiche Beiträge zum Thema Schaltnetzteile veröffentlicht.

Der Autor Franz Peter Zantis (Rufzeichen DB7FP) ist Energieanlagenelektroniker und Ingenieur der Nachrichtentechnik. In den 90er Jahren entwickelte er im Rahmen eines Forschungsprojekts eigensichere Stromversorgungsgeräte.
Heute ist er Leiter einer elektronischen Werkstatt an der RWTH (RheinischWestfälische Technische Hochschule) in Aachen. Neben dem Alltagsgeschäft beschäftigt er sich auch privat gerne mit der Elektronik.
Elektor Verlag GmbH www.elektor.de
