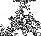Prefacetothesecond
edition
Thesecondeditionof StatisticalMechanics:Entropy,OrderParameters, andComplexity featuresoverahundrednewexercises,plusrefinement andrevisionofmanyexercisesfromthefirstedition.Themainchapters arelargelyunchanged,exceptforarefactoringofmydiscussionofthe renormalizationgroupinChapter 12.Indeed,thechaptersaredesigned tobethestablekerneloftheirtopics,whiletheexercisescoverthe growingrangeoffascinatingapplicationsandimplicationsofstatistical mechanics.
Thisbookreflects“flippedclassroom”innovations,whichIhavefound toberemarkablyeffective.Ihaveidentifiedahundredpre-classquestionsandin-classactivities,theformerdesignedtoelucidateandreinforcesectionsofthetext,andthelatterdesignedforgroup collaboration. Thesearedenotedwiththesymbols p and a ,inanextensionofthe difficultyrating 1– 5usedinthefirstedition. Humancorrelations, Fingerprints,and Cracklingnoises aresomeofmyfavoriteactivities. Theseexercises,plusaselectionofless-specializedlongerexercises,form thecoreoftheundergraduateversionofmycourse.
Extensiveonlinematerial[181]isnowavailablefortheexercises. Mathematicaandpythonnotebooksprovidehintsforalmostfiftycomputationalexercises,allowingstudentstotackleserious newresearch topicslike Conformalinvariance, SubwaybenchMonteCarlo,and 2D turbulenceandJupiter’sgreatredspot,whilegettingexposedtogood programmingpractices.Handoutsandinstructionsfacilitateactivities suchas Pentagonalfrustration and Hearingchaos.Theanswerkeyfor theexercisesnowispolishedenoughthatIregretnotbeingabletoshare itwithanybutthoseteachingthecourse.
Finally,thestrengthofthefirsteditionwasinadvancedexercises, whichexploredindepththesubtletiesofstatisticalmechanicsandthe broadrangeofitsapplicationtovariousfieldsofscience.Manysubstantiveexercisescontinuethistrend,suchas Nucleosynthesisandthe arrowoftime, WordfrequenciesandZipf’slaw, Pandemic,and Kinetic proofreadingincells
IagainthanktheNationalScienceFoundationandCornell’s physics departmentformakingpossiblethelivelyacademicatmosphereatCornellandmyamazinggraduatestudents;bothwerecrucialfor thesuccess ofthisendeavor.Thankstothestudentsandreaderswhostampedout errorsandobscurities.Thankstomygroupmembersandcolleagueswho
contributedsomeofthemostcreativeandinsightfulexercisespresented here—theyareacknowledgedinthemasterpiecesthattheycrafted. ThankstoJaronKent-Dobiasforseveralyearsofenthusiasm,insight, andsuggestions.AdebtisgratefullyduetoMattBierbaum;manyof thebestexercisesinthistextmakeuseofhiswonderfullyinteractive Ising[28]andmoshpit[32]simulations.
Enormousthanksareduetomylifelongpartner,spouse,andlove, CarolDevine,whotoleratesmyfascinationwithsolvingphysicspuzzles andturningthemintoexercises,becausesheseesitmakesme happy.
JamesP.Sethna Ithaca,NY
September2020
Preface
Thepurviewofsciencegrowsrapidlywithtime.Itistheresponsibility ofeachgenerationtojoinnewinsightstooldwisdom,andtodistillthe keyideasforthenextgeneration.Thisismydistillationof thelastfifty yearsofstatisticalmechanics—aperiodofgrandsynthesisandgreat expansion.
Thistextiscarefultoaddresstheinterestsandbackground notonly ofphysicists,butofsophisticatedstudentsandresearchersinmathematics,biology,engineering,computerscience,andthesocialsciences. Itthereforedoesnotpresumeanextensivebackgroundinphysics,and (exceptforChapter 7)explicitlydoesnotassumethatthereaderknows orcaresaboutquantummechanics.Thetexttreatstheintersectionof theinterestsofallofthesegroups,whiletheexercisesencompassthe unionofinterests.Statisticalmechanicswillbetaughtin allofthese fieldsofscienceinthenextgeneration,whetherwholesaleorpiecemeal byfield.Bymakingstatisticalmechanicsusefulandcomprehensibleto avarietyoffields,weenrichthesubjectforthosewithbackgroundsin physics.Indeed,manyphysicistsintheirlatercareersare nowtaking excursionsintotheseotherdisciplines.
Tomakeroomforthesenewconceptsandapplications,muchhas beenpruned.Thermodynamicsnolongerholdsitstraditionalkeyrole inphysics.Likefluidmechanicsinthelastgeneration,itremainsincrediblyusefulincertainareas,butresearchersinthoseareas quicklylearnit forthemselves.Thermodynamicsalsohasnothadsignificant impactin subjectsfarremovedfromphysicsandchemistry:nobodyfindsMaxwell relationsforthestockmarket,orClausius–Clapeyronequationsapplicabletocompressionalgorithms.Theseandotherimportant topicsin thermodynamicshavebeenincorporatedintoafewkeyexercises.Similarly,moststatisticalmechanicstextsrestuponexamplesdrawnfrom condensedmatterphysicsandphysicalchemistry—exampleswhichare thentreatedmorecompletelyinothercourses.EvenI,acondensed matterphysicist,findthecollapseofwhitedwarfsmorefunthanthe low-temperaturespecificheatofmetals,andtheentropyofcardshufflingstillmoreentertaining.
Thefirsthalfofthetextincludesstandardtopics,treatedwithan interdisciplinaryslant.Extensiveexercisesdevelopnew applicationsof statisticalmechanics:randommatrixtheory,stock-marketvolatility, theKAMtheorem,Shannonentropyincommunicationstheory, and Dyson’sspeculationsaboutlifeattheendoftheUniverse.Thesecond halfofthetextincorporatesMonteCarlomethods,orderparameters,
viii Preface linearresponseandcorrelations(includingaclassicalderivationofthe fluctuation-dissipationtheorem),andthetheoryofabrupt andcontinuousphasetransitions(criticaldroplettheoryandtherenormalization group).
Thistextisaimedforusebyupper-levelundergraduatesand graduatestudents.Ascientificallysophisticatedreaderwithafamiliaritywith partialderivativesandintroductoryclassicalmechanics shouldfindthis textaccessible,exceptforChapter 4 (whichdemandsHamiltonianmechanics),Chapter 7 (quantummechanics),Section 8.2 (linearalgebra), andChapter 10 (Fouriermethods,introducedintheAppendix).Anundergraduateone-semestercoursemightcoverChapters1–3, 5–7,and9. Cornell’shard-workingfirst-yeargraduatestudentscoveredtheentire textandworkedthroughperhapshalfoftheexercisesinasemester. Ihavetriedtosatisfyalloftheseaudiencesthroughtheextensiveuse offootnotes:thinkofthemasoptionalhyperlinkstomaterialthatis morebasic,moreadvanced,orasidelighttothemainpresentation.The exercisesareratedbydifficulty,from 1(doablebyinspection)to 5(advanced);exercisesrated 4(manyofthemcomputationallaboratories) shouldbeassignedsparingly.MuchofChapters1–3,5,and6wasdevelopedinansophomorehonors“wavesandthermodynamics”course; thesechaptersandtheexercisesmarked 1and 2shouldbeaccessible toambitiousstudentsearlyintheircollegeeducation.Acoursedesigned toappealtoaninterdisciplinaryaudiencemightfocusonentropy,order parameters,andcriticalbehaviorbycoveringChapters1–3,5,6,8,9, and12.Thecomputationalexercisesinthetextgrewoutofthreedifferentsemester-longcomputationallaboratorycourses.Wehopethatthe computerexercisehintsandinstructionsonthebookwebsite[181]will facilitatetheirincorporationintosimilarcourseselsewhere.
Thecurrentplanistomakeindividualchaptersavailableas PDFfiles ontheInternet.Ialsoplantomakethefiguresinthistextaccessible inaconvenientformtothosewishingtousethemincourseorlecture presentations.
Ihavespentanentirecareerlearningstatisticalmechanicsfromfriends andcolleagues.Sincethisisatextbookandnotamanuscript,the presumptionshouldbethatanyideasorconceptsexpressedarenot mine,butratherhavebecomesocentraltothefieldthatcontinued attributionwouldbedistracting.Ihavetriedtoincludereferencesto theliteratureprimarilywhenitservesmyimaginedstudent.Inthe ageofsearchengines,aninterestedreader(orwriteroftextbooks)can quicklyfindthekeyideasandarticlesonanytopic,oncethey know whatitiscalled.Thetextbookisnowmorethaneveronlyabasefrom whichtolaunchfurtherlearning.Mythankstothosewhohave patiently explainedtheirideasandmethodsovertheyears—eitherinperson,in print,orthroughtheInternet.
Imustthankexplicitlymanypeoplewhowereoftangibleassistance inthewritingofthisbook.IthanktheNationalScienceFoundation andCornell’sLaboratoryofAtomicandSolidStatePhysicsfortheir supportduringthewritingofthistext.IthankPamelaDavis Kivel-
sonforthemagnificentcoverart.IthankEannaFlanagan,EricSiggia, SaulTeukolsky,DavidNelson,PaulGinsparg,VinayAmbegaokar,Neil Ashcroft,DavidMermin,MarkNewman,KurtGottfried,Chris Henley,BarbaraMink,TomRockwell,CsabaCsaki,PeterLepage, andBert Halperinforhelpfulandinsightfulconversations.EricGrannan,Piet Brouwer,MichelleWang,RickJames,EannaFlanagan,IraWasserman,DaleFixsen,RachelBean,AustinHedeman,NickTrefethen,Sarah Shandera,AlSievers,AlexGaeta,PaulGinsparg,JohnGuckenheimer, DanStein,andRobertWeisswereofimportantassistanceindevelopingvariousexercises.Myapproachtoexplainingtherenormalization group(Chapter 12)wasdevelopedincollaborationwithKarinDahmen,ChrisMyers,andOlgaPerkovi´c.Thestudentsinmyclasshave beeninstrumentalinsharpeningthetextanddebuggingtheexercises; JonathanMcCoy,AustinHedeman,BretHanlon,andKadenHazzard inparticulardeservethanks.AdamBecker,Surachate(Yor) Limkumnerd,SarahShandera,NickTaylor,QuentinMason,andStephenHicks, intheirrolesofproofreading,grading,andwritinganswer keys,were powerfulfiltersforweedingoutinfelicities.IthankJoelShore,Mohit Randeria,MarkNewman,StephenLanger,ChrisMyers,DanRokhsar, BenWidom,andAlanBrayforreadingportionsofthetext,providing invaluableinsights,andtighteningthepresentation.IthankJulieHarris atOxfordUniversityPressforherclosescrutinyandtechnicalassistance inthefinalpreparationstagesofthisbook.Finally,ChrisMyersandI spenthundredsofhourstogetherdevelopingthemanycomputerexercisesdistributedthroughthistext;hisbroadknowledgeof scienceand computation,hisprofoundtasteincomputationaltoolsand methods, andhisgoodhumormadethisaproductiveandexcitingcollaboration. Theerrorsandawkwardnessthatpersist,andtheexcitingtopicsIhave missed,areinspiteofthewonderfulinputfromthesefriendsandcolleagues.
IespeciallythankCarolDevine,forconsultation,insightfulcomments andquestions,andfortoleratingthebackofherspouse’sheadforperhapsathousandhoursoverthepasttwoyears.
JamesP.Sethna Ithaca,NY February,2006
4Phase-spacedynamicsandergodicity 79
4.1Liouville’stheorem 79
4.2Ergodicity 81 Exercises 85
4.1Equilibration 86
4.2Liouvillevs.thedampedpendulum 86
4.3Invariantmeasures 87
4.4Jupiter!andtheKAMtheorem 89
4.5NoHamiltonianattractors 91
4.6Perverseinitialconditions 91
4.7Crooks 91
4.8Jarzynski 93
4.92DturbulenceandJupiter’sgreatredspot 94
5Entropy 99
5.1Entropyasirreversibility:enginesandtheheatdeathof theUniverse 99
5.2Entropyasdisorder 103
5.2.1Entropyofmixing:Maxwell’sdemonandosmotic pressure 104
5.2.2Residualentropyofglasses:theroadsnottaken 105
5.3Entropyasignorance:informationandmemory 107
5.3.1Nonequilibriumentropy 108
5.3.2Informationentropy 109 Exercises 112
5.1LifeandtheheatdeathoftheUniverse 113
5.2BurninginformationandMaxwelliandemons 113
5.3Reversiblecomputation 115
5.4Blackholethermodynamics 116
5.5Pressure–volumediagram 116
5.6Carnotrefrigerator 117
5.7Doesentropyincrease? 117
5.8TheArnol’dcatmap 117
5.9Chaos,Lyapunov,andentropyincrease 119
5.10Entropyincreases:diffusion 120
5.11Entropyofglasses 120
5.12Rubberband 121
5.13Howmanyshuffles? 122
5.14Informationentropy 123
5.15Shannonentropy 123
5.16Fractaldimensions 124
5.17Derivingentropy 126
5.18Entropyofsocks 126
5.19Aging,entropy,andDNA 127
5.20Gravityandentropy 127
5.21Datacompression 127
5.22TheDysonsphere 129
5.23Entropyofthegalaxy 130
7.6.2Black-bodyradiation 191
7.6.3Bosecondensation 192
7.7MetalsandtheFermigas 194 Exercises 195
7.1Ensemblesandquantumstatistics 195
7.2Phononsandphotonsarebosons 196
7.3Phase-spaceunitsandthezeroofentropy 197
7.4Doesentropyincreaseinquantumsystems? 198
7.5Photondensitymatrices 198
7.6Spindensitymatrix 198
7.7Lightemissionandabsorption 199
7.8Einstein’s A and B 200
7.9Bosonsaregregarious:superfluidsandlasers 200
7.10Crystaldefects 201
7.11Phononsonastring 202
7.12Semiconductors 202
7.13Bosecondensationinaband 203
7.14Bosecondensation:theexperiment 203
7.15Thephoton-dominatedUniverse 204
7.16Whitedwarfs,neutronstars,andblackholes 206
7.17Eigenstatethermalization 206
7.18Drawingwavefunctions 206
7.19Many-fermionwavefunctionnodes 207
7.20Coolingcoffee
7.21Thegreenhouseeffect 208
7.22Lightbaryonsuperfluids 208
7.23Whyareatomsclassical? 208
7.24Issoundaquasiparticle? 209
7.25Quantummeasurementandentropy 210
7.26Entanglementoftwospins 212
7.27Heisenbergentanglement 213
8Calculationandcomputation 217
8.1TheIsingmodel 217
8.1.1Magnetism 218
8.1.2Binaryalloys 219
8.1.3Liquids,gases,andthecriticalpoint 220
8.1.4HowtosolvetheIsingmodel 220
8.2Markovchains 221
8.3Whatisaphase?Perturbationtheory 225 Exercises 227
8.1TheIsingmodel 228
8.2Isingfluctuationsandsusceptibilities 228
8.3CoinflipsandMarkov 229
8.4Redandgreenbacteria 229
8.5Detailedbalance 229
8.6Metropolis 230
8.7ImplementingIsing 230
10.4Onsager’sregressionhypothesisandtimecorrelations
11.12Nucleationin2D
11.13Linearstabilityofagrowinginterface
12.3.1Equilibriumcriticality:energyversusentropy
12.3.2Quantumcriticality:zero-pointfluctuationsversusenergy
12.4Bifurcationtheory
12.5Mean-fieldtheory
12.10RGandthecentrallimittheorem:short 378 12.11RGandthecentrallimittheorem:long 378 12.12Percolationanduniversality 381 12.13Hysteresisandavalanches:scaling 383 12.14Cracklingnoises 384 12.15Hearingchaos 385 12.16Perioddoublingandtheonsetofchaos 386 12.17TheGutenberg–Richterlaw 386 12.18Randomwalksanduniversalexponents 386 12.19Diffusionequationanduniversalscalingfunctions 387 12.20HysteresisandBarkhausennoise 388 12.21Earthquakesandwires 388 12.22Activatedratesandthesaddle-nodetransition 389 12.23Biggestofbunch:Gumbel 391 12.24Extremevalues:Gumbel,Weibull,andFr´echet 392 12.25Criticalcorrelations 393 12.26Isingmeanfieldderivation 394 12.27Mean-fieldboundforfreeenergy
12.28Avalanchesizedistribution
12.29Theonsetofchaos:lowestorderRG
12.30Theonsetofchaos:fullRG 397 12.31Singularcorrectionstoscaling 398 12.32Conformalinvariance 399
A.2Derivatives,convolutions,andcorrelations
A.3Fouriermethodsandfunctionspace
A.4Fourierandtranslationalsymmetry
A.1Soundwave
A.2Fouriercosines
A.3Doublesinusoid
A.4FourierGaussians
A.5Uncertainty
A.6Fourierrelationships
A.7Aliasingandwindowing
Listoffigures
2.8EffectivepotentialformovingalongDNA
3.6Excludedareaaroundaharddisk
6.8Densityfluctuationsinspace
6.9Coarse-graineddensityinspace
6.10Negativetemperature
6.11RNApolymerasemolecularmotor
6.12HairpinsinRNA
6.13TelegraphnoiseinRNAunzipping
6.14Genericphasediagram
6.15Wellprobabilitydistribution
6.16Crossingthebarrier
6.17Michaelis–MentenandHillequationforms
6.18Squarepollen
6.19Pistonwithrubberband
6.20Pistoncontrol
6.21Zipf’slawforwordfrequencies
7.1Thequantumstatesoftheharmonicoscillator
7.2Thespecificheatforthequantumharmonicoscillator 184
7.3Feynmandiagram:identicalparticles
7.4Bose–Einstein,Maxwell–Boltzmann,andFermi–Dirac 186
7.5TheFermidistribution f (ε)
7.6Particleinabox
7.7 k-sphere
7.8ThePlanckblack-bodyradiationpowerspectrum
7.9Bosecondensation
7.10TheFermisurfaceforlithium
7.11TheFermisurfaceforaluminum
7.12Microcanonicalthreeparticles
7.13Canonicalthreeparticles
7.14Grandcanonicalthreeparticles
7.15Photonemissionfromahole
7.16Bose–Einsteincondensation
7.17Planckmicrowavebackgroundradiation
8.1The2Dsquare-latticeIsingmodel
8.2Isingmagnetization
8.3TheIsingmodelasabinaryalloy
8.4 P –T phasediagram
8.5 H–T phasediagramfortheIsingmodel
8.6BoseandFermispecificheats
8.7Perturbationtheory
8.8Oil,water,andalcohol
8.9Clusterflip:before
8.10Clusterflip:after
8.11Dimerizationreaction
8.12Biologyrepressilator
8.13Computationalrepressilator
8.14Barkhausennoiseexperiment
8.15Hysteresisloopwithsubloops
10.16Telegraphnoiseinametallicnanojunction
10.17Telegraphnoisewiththreemetastablestates
11.1 P –T and T –V phasediagrams
11.2Stableandmetastablestates
11.3Maxwellequal-areaconstruction
11.5Freeenergybarrier
11.6Equilibriumcrystalshape
11.7Coarsening
11.8Curvature-driveninterfacemotion
11.9Coarseningforconservedorderparameter
11.10Logarithmicgrowthofaninterface
11.11Martensite
11.12Dendrites
11.13 P –V plot:vanderWaals
11.14Chemicalpotential:vanderWaals
11.20Crystalshapecoordinates
Whatisstatistical mechanics? 1
Manysystemsinnaturearefartoocomplextoanalyzedirectly.Solving forthebehaviorofalltheatomsinablockofice,orthebouldersinan earthquakefault,orthenodesontheInternet,issimplyinfeasible.Despitethis,suchsystemsoftenshowsimple,strikingbehavior.Statistical mechanicsexplainsthesimplebehaviorofcomplexsystems.
Theconceptsandmethodsofstatisticalmechanicshaveinfiltrated intomanyfieldsofscience,engineering,andmathematics:ensembles, entropy,MonteCarlo,phases,fluctuationsandcorrelations,nucleation, andcriticalphenomenaarecentraltophysicsandchemistry,butalso playkeyrolesinthestudyofdynamicalsystems,communications,bioinformatics,andcomplexity.Quantumstatisticalmechanics,althoughnot asourceofapplicationselsewhere,isthefoundationofmuchofphysics. Letusbrieflyintroducethesepervasiveconceptsandmethods.
Ensembles. Thetrickofstatisticalmechanicsisnottostudyasingle system,butalargecollectionor ensemble ofsystems.Whereunderstandingasinglesystemisoftenimpossible,onecanoftencalculatethe behaviorofalargecollectionofsimilarlypreparedsystems.
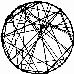
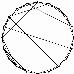
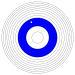
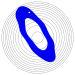
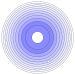
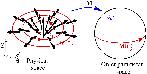
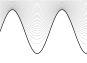
Forexample,considerarandomwalk(Fig. 1.1).(Imagineitasthe trajectoryofaparticleinagas,ortheconfigurationofapolymerin solution.)Whilethemotionofanygivenwalkisirregularandtypically impossibletopredict,Chapter 2 derivestheelegantlawswhichdescribe thesetofallpossiblerandomwalks.
Chapter 3 usesanensembleofallsystemstatesofconstantenergy toderiveequilibriumstatisticalmechanics;thecollectivepropertiesof temperature,entropy,andpressureemergefromthisensemble.InChapter 4 weprovidethebestexistingmathematicaljustificationfor using thisconstant-energyensemble.InChapter 6 wedevelop freeenergies whichdescribepartsofsystems;byfocusingontheimportantbits,we findnewlawsthatemergefromthemicroscopiccomplexity.
Entropy. Entropyisthemostinfluentialconceptarisingfromstatisticalmechanics(Chapter 5).Itwasoriginallyunderstoodasathermodynamicpropertyofheatenginesthatinexorablyincreaseswith time.Entropyhasbecomescience’sfundamentalmeasureofdisorder andinformation—quantifyingeverythingfromcompressingpictureson theInternettotheheatdeathoftheUniverse.
Quantumstatisticalmechanics,confinedtoChapter 7,provides themicroscopicunderpinningtomuchofastrophysicsandcondensed StatisticalMechanics:Entropy,OrderParameters,andComplexity. JamesP.Sethna,Oxford UniversityPress(2021). c JamesP.Sethna.DOI:10.1093/oso/9780198865247.003.0001
2 Whatisstatisticalmechanics?
Fig.1.1Randomwalks.Themotionofmoleculesinagas,andbacteria inaliquid,andphotonsintheSun,are describedby randomwalks.Describing thespecifictrajectoryofanygivenrandomwalk(left)isnotfeasible.Describingthestatisticalpropertiesofalarge numberofrandomwalksisstraightforward(right,showingendpointsofmany walksstartingattheorigin).Thedeep principleunderlyingstatisticalmechanicsisthatitisofteneasiertounderstandthebehaviorofthese ensembles ofsystems.
matterphysics.Thereweuseittoexplainmetals,insulators,lasers, stellarcollapse,andthemicrowavebackgroundradiationpatternsfrom theearlyUniverse.
MonteCarlo methodsallowthecomputertofindensembleaverages insystemsfartoocomplicatedtoallowanalyticalevaluation.These tools,inventedandsharpenedinstatisticalmechanics,areusedeverywhereinscienceandtechnology—fromsimulatingtheinnards ofparticle accelerators,tostudiesoftrafficflow,todesigningcomputercircuits.In Chapter 8,weintroduceMonteCarlomethods,theIsingmodel,andthe mathematicsofMarkovchains.
Phases. Statisticalmechanicsexplainstheexistenceandpropertiesof phases.Thethreecommonphasesofmatter(solids,liquids, andgases) havemultipliedintohundreds:fromsuperfluidsandliquidcrystals,to vacuumstatesoftheUniversejustaftertheBigBang,tothepinnedand sliding“phases”ofearthquakefaults.Weexplainthedeepconnection betweenphasesandperturbationtheoryinSection 8.3.InChapter 9 weintroducethe orderparameterfield,whichdescribestheproperties, excitations,andtopologicaldefectsthatemergeinagiven phase.
Fluctuationsandcorrelations. Statisticalmechanicsnotonlydescribestheaveragebehaviorofanensembleofsystems,itdescribes theentiredistributionofbehaviors.Wedescribehowsystemsfluctuate andevolveinspaceandtimeusing correlationfunctions inChapter 10 Therewealsoderivepowerfulandsubtlerelationsbetweencorrelations, response,anddissipationinequilibriumsystems.
Abruptphasetransitions. Beautifulspatialpatternsariseinstatisticalmechanicsatthetransitionsbetweenphases.Most suchtransitionsareabrupt;iceiscrystallineandsoliduntil(attheedgeofthe icecube)itbecomesunambiguouslyliquid.Westudythenucleation