QuantumStochasticThermodynamics
FoundationsandSelectedApplications
PhilippStrasberg
UniversitatAut` onomadeBarcelona
ThisbookisdedicatedtothememoryofmyPhDsupervisor,TobiasBrandes
Preface
Recentdecadeshaveseenmuchprogressinourunderstandingofthermodynamicprocessesatthenanoscale.Butnanoscalesystemsareverysmall,inmostapplications farfromequilibrium,oftensubjecttostrongfluctuationsandsometimesevencharacterizedbyexoticquantumproperties—soitseemsthatthesefeaturesruleoutany possibilityoffindingaconsistentthermodynamicdescriptionforthem.
Itistheprimaryobjectiveofthisbooktoshowthatthisisnotthecase.Thereisa thermodynamicframework,characterizedbyaremarkableinternalconsistency,that isabletodescribenanoscalesystemsevenunderextremeconditions.Moreover,this frameworknotonlyreaffirmscommonfolklorearoundthermodynamics(thereisno perpetualmotionmachine,etc.),butalsoprovidesawealthofbeautifulresultsbeyond thetraditionalscopeofthermodynamics—openingupthepossibilityofunderstanding aplethoraofdifferentphysicalsituationsfromaunifiedperspective.
Themaintitle QuantumStochasticThermodynamics suggeststhatthepresent bookisaboutasynthesisoftworesearchfields:classicalstochasticthermodynamics andquantumthermodynamics.Bothhavepushedtheboundariesoftheapplicabilityof thelawsofthermodynamicsbyexplainingandsupplementingthemwithmicroscopic considerations.Foraconsiderablelargeclassofnanoscalesystemsandprocesses,I believethatmostfoundationalquestionshavebeensettledbynow.Thepresentbook isintendedtofillagapintheliteraturebyjustifyingthisclaimindetailforalarge varietyofsituations.Iamalsoconvincedthatitscontentwillproveimportantin exploringnewterritoriesattherapidlyevolvingfrontiersofthisfield.
Thesubtitle FoundationsandSelectedApplications emphasizesthatthereadercan mainlyexpectexplanationsaboutthebasictheoreticalpillars.Theseexplanationsare intendedtobepedagogicallyaccessible.However,thebookisalsodrivenbythedesire tointroduceageneralandversatileframeworkcharacterizedbyconceptualclarity— incompleteawarenessofthefactthatthisposesadditionaltechnicalobstaclesfor thebeginner.Toremedythis,aconsiderableefforthasbeenmadetotransparently explaincommon‘jargon’inthecommunity(non-equilibriumentropies,localdetailed balance,Landauer’sprinciple,entropyproduction,time-reversalsymmetry,thearrow oftime,etc.),whichoftenappearsunnecessarilymystifying(aproblemthatseemsto haveatraditioninthermodynamicsandstatisticalmechanics).Thereaderwilloften findthesame(orcloselyrelated)resultsderivedindifferentwaysinordertogenerate confidenceandtrustintheframework.
Thefieldofquantumstochasticthermodynamicsis,however,fascinating,notonly becauseitallowsustoaddresssfoundationalquestionsaboutthenatureofheat, entropyorthesecondlaw,butalsobecauseitmighthavedirectpracticalapplications inaworldwithincreasingnanotechnologicalabilities.Theseapplicationscouldcome intheformofefficientthermoelectricdevices,powerfulenergyharvesters,fastcooling
HowtoReadthisBook vii strategies,orenergy-efficientcomputers,amongothermoreexoticapplications.To formacloseconnectionbetweenfoundationalandpracticalproblems,thisbooktreats afewselectedapplicationsindetail.
Unfortunately,becauseofalackoftimeandunderstandingontheauthor’sside, thisbookcannotcoverallpossibledirectionsthatarecurrentlyunderinvestigation. TheselectedmaterialisobviouslybiasedandIaskforforbearancefrommymany colleagueswhofeelthatthepresentbookmissessomeimportantideas.
HowtoReadthisBook
Thisbookiswrittenforgraduatestudentswhoknowthebasicsofquantummechanics andequilibriumstatisticalmechanicsandwhocannotwaittocombinethesefieldsto understandnon-equilibriumphenomena.Asaruleofthumb,youarereadytodelve intothebookifthefollowingequationsdonotscareyouoff:
Ofcourse,thisbookisalsowrittenformoreexperiencedresearchers.Ihopethatthey willhavenotroubleinjumpingbetweendifferentsectionsofthisbook(thoughitmight helptofirstlookattheBasicNotationsectionbelow).Tobecomefurtheracquainted withthebook,Isummarizehereitsmostimportantfeatures.
Structureofthebook: Togetacompletepicture,Ibelieveoneshouldsooneror laterreadtheentirebookand,then,itwouldperhapsbemostbeneficialtogothrough itinlinearorder.However,Ialsobelievethattheimpatientreadershouldnotbeafraid toskipsectionsorchapters.Forinstance,Chapter 1 (QuantumStochasticProcesses) appearstobethemostabstractone,inparticularitssecondhalf.WhileIbelievethat thismoreabstractpointofviewhelpstoviewtheentirefieldinaclearandunified way,itiscertainlynotnecessarytoreachanunderstandingofChapter 2 (Classical StochasticThermodynamics),whichsolelyrequiressomebasicbackgroundknowledge ofthetheoryofclassicalstochasticprocesses.Likewise,readerswithsomefamiliarity withopenquantumsystemtheorycandirectlystartreadingChapter 3 (Quantum ThermodynamicsWithoutMeasurements).TounderstandChapter 4 (QuantumFluctuationTheorems),somebackgroundinformationfrompreviouschaptersisrequired. ForsomesectionsofChapter 5 (OperationalQuantumStochasticThermodynamics) itisnecessarytohavealsoreadandunderstoodtheendofChapter 1.Finally,three appendicescomplementthisbookbyprovidinginformationabouttopicsthatappear
viii Preface
atvariouspointsinthemaintext,butwhosedetailedexpositionrequiresalonger detour,whichwouldblurthemainnarrative.
Structureofthesections: Typically,Ihavetriedtostarteachsectionwith asmallparagraphmotivatingitscontentandtoendeachsectionwithasmallsummaryoroutlook.Tofacilitateorientation,somesections(inparticularlongerones)are dividedintosubsectionsusingunnumberedsubtitles.Furthermore,importantstatementsaredistinguishedbylongeritalictextandboxedequationshighlightimportant definitionsorresults.
Index: Ihavetriedtomakealongandinformativeindexlist.Wordsorphrases appearinginthislistareprintedina boldface fontinthemaintextatthepoint wheretheyarefirstintroducedorexplained.However,asIsaidabove,thebookis characterizedbypresentingsimilarconceptsindifferentcontextsandfromdifferent perspectives.Thus,thebookisnotwrittenasanencyclopaedia,buttriestomaintain anarrativethatismostbeneficialforpedagogicalpurposes.
Exercises: Variousexercisesarescatteredthroughoutthetext.Theseexercises,sometimessupplementedby(hopefully)helpfulhintsonhowtosolvethem,shouldberather simplebecauseIbelievethereisnobenefitintorturingthereader.Exercisesfall,however,intotwocategories.Thefirstcategoryofexercisesaretheshortones.Theyare supposedtosupplysimplecross-checksforthereaderor,byaskingforderivationsof someequations,toacquaintthereaderwithstandardmathematicalmanipulationsin thefield.Then,therearealsovariouslongerexercises,whichmightevenrequiresome simplesymbolicprogramming.Theselongerexercisesaretypicallymeanttointroduce ideas,conceptsorresultswhosedetailedexpositionwouldprobablyborethemoreexperiencedreaderinthefield.Thus,theexerciseshelptokeepthebookmoreconcise, whileallowingmeatthesametimetocoverawiderrangeoftopics.Iremarkthatall exercisesappearduringthetextatthepointwheretheybestfittheoverallnarrative.
References: Incontrasttotheexercises,allreferencesarerelegatedtoaspecial Furtherreadingsectionattheendofeachchapter.Havingtheoverallpedagogical purposeofthebookinmind,Iindeedbelievethatthereislittlebenefitfrommentioning referencesduringthemainexpositionofthematerial.Moreover,itoughttobeclear that,giventhebreadthandscopeofthepresentbook,itisimpossibletogivecredit toallcontributionsand,seenagainfromapedagogicalperspective,Ibelievethereis littlebenefitfromtryingtodosohere.Hence,thisbookshouldnotbeconfusedwith aconventional‘reviewarticle’.Mostcitationsaregiventothelatestwork,wherethe mainconceptsorequationsIrelyonwerefirstintroducedorderived.Othercitations typicallyrefertoexpositionsthatgobeyondthematerialpresentedhereinawider sense(i.e.books,reviewsorintroductoryarticlesaboutfieldsrelatedtobutnotpartof quantumstochasticthermodynamics).Finally,somecitationsareaddedforhistorical clarity.Thus,theoverallideaisthatthelistofreferencesprovidesafirst orientation forthenewcomer,notanexhaustivelistofcontributionstothefield.
BasicNotation ix
BasicNotation
Itriedtokeepabbreviationstoaminimumandusedonlythosethatarewidely usedintheliterature.Thethreemostimportantabbreviations,whicharescattered throughoutthetext,areCP(completelypositive),CPTP(completelypositiveand trace-preserving)andBMS(Born–Markovsecular).Insomeequations,Iwriteh.c.to denotetheHermitianconjugate.AlsotheabbreviationPOVM(positiveoperatorvaluedmeasure)isusedoccasionally.
Below,Ifurtherprovideanon-exhaustivelistofthemostimportantnotationused throughoutthebook.
Generalmathematics: Matricesaredenotedbycapitalletters(suchas M ).Boldfacelettersareusedforvectors(e.g.avectorofprobabilities p)andsequences(e.g. asequenceofmeasurementresults r),buttheirelementsarewrittenas,forexample, pj or rn.Multiplicationofvectorsandmatricesiswrittenwithoutadot(e.g. M p). [A,B]= AB BA and {A,B} = AB + BA denotethecommutatorandanticommutator,respectively.Asuperscript ∗, T or † denotesthecomplexconjugate, transposeortheconjugatetranspose,respectively.Theimaginaryunitisdenoted i andthesymbol O(x) denotesthatlimx→0 |O(x)/x| < ∞.Totalandpartialderivatives (e.g.withrespecttotime t)appearinginin-lineequationsarewrittenas dt and ∂t, respectively.FrequentlyusedfunctionsincludetheHeavisidestepfunction Θ(x),the Kroneckerdelta δm,n andtheDiracdeltafunction δ(x y).
Quantumdynamics: IuseDiracnotationforstates |ψ andtheirconjugatetranspose ψ| thatliveinaHilbertspace H anditsdual,respectively.Thescalarproductis writtenas ϕ|ψ .Toavoidunwantedtechnicalities,IassumeHilbertspacesare(or canbeapproximatedtobe)finitedimensional: d = dim H < ∞.Thedensitymatrix istypicallydenotedby ρ,whereasmostotheroperatorsaredenotedbycapitalletters suchas H,P,X,... and I istheidentity.Exceptionsarethefamiliarbosonicand fermioniccreationandannihilationoperators(denotedtypicallyby a(†),b(†),c(†),d(†)) andthePaulimatrices:
Thetraceofsomeoperator O isdenotedtr{O}.Superoperators(alsosimplycalled maps),whichmapoperatorsontooperators,arealwaysdenotedbycalligraphicletterssuchas C, D, L,... .Thetensorproductisdenoted ⊗ andadditionalsubscripts A,B,S... areusedtoindicateonwhichsubspacesomeoperatorisacting(e.g. ρS )or todenotethepartialtrace(e.g.trB { }).
Statisticalmechanics: Equilibriumconceptsaredenotedbycalligraphicletters suchastheequilibriuminternalenergy U orequilibriumentropy S.Exceptionsare parameterssuchastemperature T orchemicalpotential µ.Out-of-equilibriumquantitiesaredenotedby,forexample, U and S iftheyrefertosomeexpectationvalue orensembleaverage.ThermodynamicquantitiesdefinedalongsinglestochastictrajectoriesaredenotedbysmallLatinletters(e.g. u and s).Thecanonicalensemble(or
x Preface
Gibbsstate)isdenotedbytheGreekletter π.Forinstance, πS (β) denotestheGibbs stateofsomesystem S atinversetemperature β.
Finally, everyprocessstartsattheinitialtime t0 =0.Moreover,Ido not setBoltzmann’sandPlanck’sconstants kB and¯h to1.Ibelievethatthismakesthephysical contentofmanyequationsmoreinsightful.Forpracticalmanipulations,thischoiceis, ofcourse,notthemostconvenientone,butsincethemajorityoftheliteraturesets kB ≡ 1 and¯h ≡ 1,Ithoughtitwouldbegoodtokeepthemexplicithere.
Acknowledgements
ThisbookisdedicatedtothememoryofTobiasBrandesbecause—longbeforeIenjoyedbeinghisPhDstudent—hisinspiringandunprecedentedlectureswerethereason whyIactuallyturnedtowardstheoreticalphysics.Inmyopinion,Tobias’sapproach tophysicswasdual,tacklingdeepandconceptualproblemswhilehavingatthesame timeaneyeonexperimentallywell-groundedapproachesandmodels,whichalsowork ‘inpractice’.Iviewmyownresearch,andinparticularthisbook,inthetraditionof hisphilosophy,perhapswithsomebiasmoretowardsconceptualandgeneralideas.I hopeTobiaswouldhaveenjoyedreadingit.
ConcerningthetopicsexposedhereIfurtherowemuchofmydetailedknowledge toMassimilianoEspositoandGernotSchaller.Neithereverhesitatedtosharetheir insightsandideaswithmeaboutvarioustopicsinstatisticalmechanics,stochastic thermodynamics,non-equilibriumphysicsandopenquantumsystems.Muchoftheir knowledgeisreflectedhere;yet,IbelieveIsucceededinalsoaddingmyowntwist.
AspecialthanksgoestoKavanModi.Ashort,butinretrospectimportant,discussionattheKavliInstituteinSantaBarbarain2018inspiredmetolookatthe problemfromadifferentangleandpartofthematerialpresentedinChapter 5,and insomesensethemotivationtowritethisbook,isaconsequenceofthatdiscussion. Manymorecolleagueshavesharedtheirinsightsandthoughtswithme.Thoseon whomIcouldparticularlyrelyconcerningthetopicspresentedinthisbookinclude RobertAlicki,JanetAnders,FelipeBarra,VictorBastidas,JavierCerrillo,LuisCorrea,MaríaGarcíaDíaz,DavidGelbwaser-Klimovsky,JohnGoold,GiacomoGuarnieri, GéraldineHaack,ChristopherJarzynski,MatteoLostaglio,MarkMitchison,Kavan Modi,WolfgangMuschik,JuanParrondo,MartíPerarnau-Llobet,MatteoPolettini, AndreuRiera-Campeny,FelixRitort,ÀngelRivas,DominikS̆afránek,RafaelSánchez, AnnaSanpera,UdoSeifert,MichalisSkotiniotis,ChristopherWächtlerandAndreas Winter.ItmakesmeabitsadtoknowthatIprobablyforgottocorrectlyacknowledge allthepeoplewhocontributedtomyactualunderstandingofthistopic.Therewere clearlymanymorepeoplewhoinfluencedmythinking.
Furthermore,sincewritingabookisquitea‘mammothproject’,Iamgratefulto JavierCerrillo,MarcoMerkli,KavanModi,AndreuRiera-Campeny,ÀngelRivasand RafaelSánchez,whoread(partsof)earlydraftsofthebookandprovidedvaluable comments.Inparticular,aspecialthanksgoestoTeresaReinhardformakingsure thatvariouspartsofthebookdonotsoundtoocryptictotheoutsider.
IalsowanttothanktheteamatOxfordUniversityPress.Inparticular,Imuch appreciatedtheuncomplicatedmannerofcommunicatingwiththem,whichclearly contributedtothefactthatthewritingofthisbookwasanoverallveryjoyfulexperience.
xii Acknowledgements
Ofcourse,theconstantsupportIreceivefrommyfamilyandfriends,includingthe littlelion,areinvaluable.
MostpartsoftheworkreportedherewerefinanciallysupportedbytheDFG (projectSTR1505/2-1).ForfurthersupportIthanktheSpanishAgenciaEstatal deInvestigación,projectsIJC2019-040883-IandPID2019-107609GB-I00,theSpanishMINECOFIS2016-80681-P(AEI/FEDER,UE)andtheGeneralitatdeCatalunya CIRIT2017-SGR-1127.
Finallyandalmostneedlesstosay,allmistakesandopinionsexpressedhereareentirely myown.Iamalwaysgratefultoreceivefurthercomments,questionsandfeedback(to getincontactwithmeIsuggestyoutypemynameintoyourpreferredsearchengine andlookupmyup-to-dateemailaddress).Erratawillbeannouncedonmyhomepage.
1QuantumStochasticProcesses
1.1IsolatedQuantumSystems
1.4QuantumMeasurementTheory
1.5Operations,InterventionsandInstruments
1.6ClassicalStochasticProcesses
1.7QuantumStochasticProcesses
1.8QuantumMarkovProcessesandDynamicalMaps
1.9ClassicalQuantumStochasticProcesses
2ClassicalStochasticThermodynamics
2.3ClassicalMarkovProcessesandLocalDetailedBalance
2.4FluctuatingInternalEnergy,Heat,WorkandEntropy 61
2.5Coarse-GrainingandTime-ScaleSeparation
2.6Time-ReversedTrajectoriesandFluctuationTheorems
2.7WorkFluctuationTheorems
2.8StrongCouplingCorrections
3QuantumThermodynamicsWithoutMeasurements
3.1MechanicalWorkintheQuantumRegime 104
3.2QuantumMasterEquationsintheWeakCouplingRegime 108
3.3PropertiesoftheBorn–MarkovSecularMasterEquation 116
3.4ThermodynamicsintheBorn–MarkovSecularApproximation 119
3.5WorkExtractionfromSmallSystems 124
3.6CorrelationsandtheZerothLawofThermodynamics 130
3.7ExactDissipationInequalities 135
3.8NonequilibriumEntropy,EntropyProductionandFiniteBaths 140
3.9Non-EquilibriumResourcesandRepeatedInteractions 149
3.10ParticleTransportandThermoelectricDevices 158 Furtherreading 172
4QuantumFluctuationTheorems 175
4.1Two-PointMeasurementScheme 175
4.2WorkFluctuationTheoremsforQuantumSystems 179
xiv Contents
4.3ExchangeandFurtherFluctuationTheorems
4.4CountingFieldMethodsforQuantumMasterEquations
4.5StochasticQuantumJumpTrajectories
4.6ThermodynamicUncertaintyRelations
4.7(Impossibilityof)CarnotEfficiencyatFinitePower
4.8ThirdLawofThermodynamics
Furtherreading
5OperationalQuantumStochasticThermodynamics
5.1ClassicalityofQuantumFluctuationTheorems
5.2ANo-GoTheorem
5.3ThermodynamicsofQuantumMeasurements
5.4StochasticThermodynamicsofQuantumMarkovProcesses
5.5Maxwell’sDemonandtheThermodynamicsofFeedbackControl
5.6AutonomousApproachandStrongCouplingCorrections
5.7ApplicationtoPhotonNumberStabilizationExperiments
6Outlook
AppendixAConceptsfromInformationTheory
B.1NumericallyConvenientSuperoperatorMapping
C.1Time-ReversalSymmetryinClassicalMechanics
C.2Time-ReversalSymmetryinQuantumMechanics
QuantumStochasticProcesses
Summary. Thischapterdescribesthebasicfeaturesofopenquantumsystems,i.e. quantumsystemsthatareaffectedbynoiseduetouncontrollabledegreesoffreedom ofanenvironmentorbath.Thisnoiseisresponsibleforeffectssuchasdissipation, decoherenceandirreversibility.Westudytheequilibriumstatesofopenquantum systemsandreviewtoolsfromquantummeasurementtheory,whichdescribehow toextractinformationfroman(open)quantumsystem.Wegeneralizethesetools tomulti-timestatisticsanddefinethenotionofaquantumstochasticprocessand aquantumMarkovprocess.Finally,westudyinwhichcasesaquantumstochastic processlooksclassical.
1.1 IsolatedQuantumSystems
Time-independentcase
AquantumsystemisdescribedbyaHilbertspace H andastate ρ calledthedensity matrix,whichactsonthatspace.Thedensitymatrixischaracterizedbythefacts thatitisHermitian, ρ† = ρ (with † denotingtheHermitianconjugate),hasunittrace, tr{ρ} =1,andispositive, ρ ≥ 0.Here,thenotation ρ ≥ 0 isshorthandfor ψ|ρ|ψ ≥ 0 forall |ψ ∈H. Thestateofanisolatedquantumsystem,i.e.aquantumsystemwhichisnotin contactwithanyotherpartoftheworld,obeystheLiouville–vonNeumannequation
Here, H istheHamiltonianoperatorcharacterizingthetotalenergyofthesystemand [A,B] ≡ AB BA isthecommutator.Furthermore, i and¯h arethefamiliarimaginary unitandPlanck’sconstant,respectively.Notethatwewillalsousethenotation ∂tρ(t) todenoteapartialderivativewithrespecttotime.
Isolatedquantumsystemshavesomeimportantcharacteristics:
(i) Thereexistsaunitarytimeevolutionoperator U (t) ≡ exp( iHt/h),whichmeans that U (t)U (t)† = U (t)†U (t)= I,where I denotestheidentitymatrix.Thistime evolutionoperatorpropagatesthesystemstateaccordingto
ρ(t)= U (t)ρ(0)U (t)† , (1.2) where ρ(0) denotestheinitialstateofthequantumsystem.
QuantumStochasticThermodynamics.PhilippStrasberg,OxfordUniversityPress. ©PhilippStrasberg(2021).DOI:10.1093/oso/9780192895585.003.0001
QuantumStochasticProcesses
(ii) Thespectrumofthestate ρ(t),i.e.itseigenvalues λk,donotchangeintime: ρ(t)= k λk|ψk(t) ψk(t)|. (1.3)
Here, λk istimeindependentand |ψk(t) belongstoanorthonormalbasisof wavefunctions,i.e. ψk(t)|ψℓ(t) = δk,ℓ withtheKroneckerdelta δk,ℓ.Note thatthespectrumcanbedegenerate,i.e.itispossiblethat λk = λℓ forsome k = ℓ.Equation(1.3)followsfromthefactthatanyunitarytransformationofthe form(1.2)leavesthespectruminvariantsincethecharacteristicpolynomialdoes notchange:
det{ρ(t) λI} = det{U (t)[ρ(0) λI]U (t)†} = det{ρ(0) λI} (1.4)
Here,det{ } denotesthedeterminantofamatrix.
(iii) Thepurityof ρ(t),whichmeasuresthe‘mixedness’ofastateandisdefinedas tr{ρ2},isconserved.Thisfollowsimmediatelyfrompoint(ii)aboveor,alternatively,fromeqn(1.1)andthefactthatthetraceiscyclic,i.e.tr{ABC} = tr{CAB}.Inparticular,iftheinitialstateispure,i.e.tr{ρ(0)2} =1,wehave ρ(t)= |ψ(t) ψ(t)| forsomewavefunction |ψ(t) .Thiswavefunctionevolvesin timeaccordingtothefamiliarSchrödingerequation: ∂ ∂t |ψ(t
SincetheSchrödingerequationcanbeappliedtocomputethetimeevolutionof anyofthe |ψk(t) ineqn(1.3),itisequivalenttotheLiouville–vonNeumann equation(1.1).
(iv) The vonNeumannentropy ofthesystem,whichisdefinedas
isconstantintime.Thisfollowsagainfrompoint(ii)abovebecause SvN[ρ(t)]= k λk ln λk,whichimpliesthatthevonNeumannentropyquantifiestheclassicaluncertaintyaboutthestateofthesystem.Alternatively,theconservationof vonNeumannentropyfollowsbyusing
andeqn(1.1).Notethateqn(1.7)holdsonlyiftherankofthedensityoperator doesnotchangeduringtheevolution,whichisguaranteedbypoint(ii)above.If therankchangesintime,thevonNeumannentropyisnotdifferentiable.Note thatweuseasubscript‘vN’forthevonNeumannentropythroughoutthebook becausewewanttodistinguishitfromthenotionof thermodynamic entropy introducedlateron.Readersunfamiliarwithinformation-theoreticconceptsof entropycanfindanoverviewinAppendix A.
System–BathTheoriesandtheOriginofNoise 3
Time-dependentcase
Quantumsystemsareoftensubjectedtotime-dependentfieldsinalaboratory,and thesefieldscanbetreatedsemiclassically(e.g.laserlight).Inthiscase,theHamiltonianbecomestimedependentandisdenotedby H(λt),wherethetime-dependent parameter λt specifiestheexternalfields.Wepreferthenotation H(λt) insteadof H(t) toavoidanypossibleconfusionwiththeHeisenbergpicture.Inthefollowing, λt iscalleda driving or controlprotocol andthestateofsucha drivensystem evolves intimeaccordingtotheLiouville–vonNeumannequation(1.1)with H replacedby H(λt)
Theevolution ρ(t)= U (t, 0)ρ(0)U †(t, 0) isstilldescribedbyaunitaryoperator U (t, 0),butitsexplicitcomputationisnowmorecomplicated.Formally,wehave
whereweabbreviated λtj ≡ λj andthesubscript + denotestimeordering.Bydividing thetimeinterval [0,t] into n = t/δt smallsteps δt,wecanalsowrite
whichbecomesexactinthelimit n →∞
Strictlyspeaking,adrivenquantumsystemisnotisolatedasitisincontactwith theexternaldrivingfield.However,itiseasytocheckthatpoints(i)–(iv)abovearestill satisfiedforsuchadrivensystem.Incontrast,thetimeevolutionofaquantumsystem whichinteractswithanotherquantumsystemismarkedlydifferent,aswewillseein therestofthischapter.Therefore,itseemswisetocallaquantumsystem‘isolated’ aslongasitevolvesintimeaccordingtotheLiouville–vonNeumannequation(1.1), whethertheHamiltonianistimeindependentornot.
1.2 System–BathTheoriesandtheOriginofNoise
Inreality,nobodyhaseverobservedanisolatedquantumsystemattheveryend becausethemereactof‘observing’aquantumsystemrequiresittobecoupledwithan externaldetector.Wewill,however,postponethediscussionofquantummeasurement theorytoSection 1.4 andarehereratherconcernedwiththefactthatmanyquantum systemsinteractwith uncontrollable degreesoffreedomofaso-called environment or bath.Oneexampleisanatom(the‘system’)interactingwiththemanyelectromagnetic modesofthesurroundingspace(the‘environment’).Anotherexampleisasinglespin, e.g.animpurityinametalorcrystal,interactingwithmanyremainingspinsand
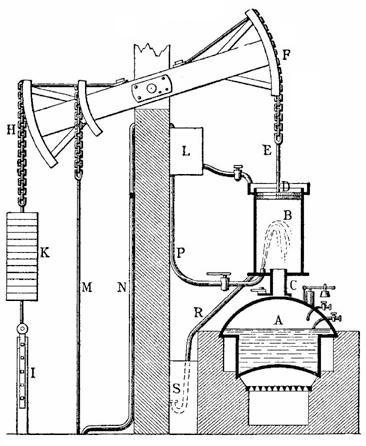
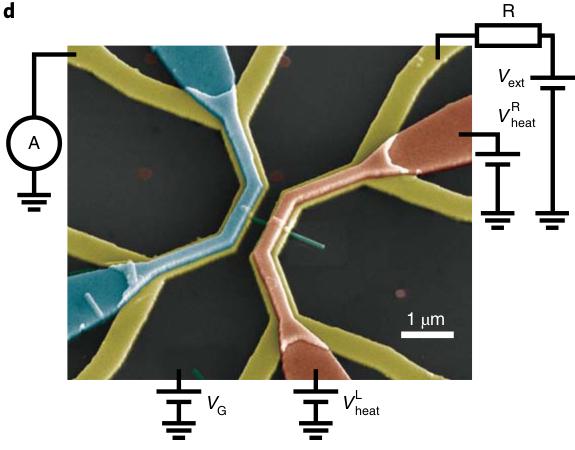
Fig.1.1 Openquantumsystems.(a)Aroughsketchofasystem S incontactwithabath B withwhichitcanexchangeenergies,particles,entropy,etc.(b)DiagramoftheNewcomenatmosphericsteamengineasanexampleofanancient‘openquantumsystem’:thermodynamics hadalreadydividedtheuniverseintoasystempartandreservoirs.(c)(False-coloured)scanningelectronmicroscopeimageofamodernopenquantumsystem:aquantumdotformedby ananowire(thingreenline)incontactwithelectronreservoirs(yellow)andheaters(blueand red).SuchsetupswillbetreatedinfurtherdetailinSection 3.10.Reprintedbypermission fromSpringerNature:SpringerNature, NatureNanotechnology (Aquantum-dotheatengine operatingclosetothethermodynamicefficiencylimits,M.Josefssonetal.),Copyrightby SpringerNature(2018).
phonons(latticevibrations)inthesurroundings.Finally,thehistoricaloriginofthe theoryofthermodynamicsisrootedinthedesiretounderstand,forexample,steam inacontainerincontactwithhotairproducedbyburningcoalontheonesideand coldwaterontheotherside.Here,thesystemisdefinedbythecontainer,which containstheso-calledworkingmediumorworkingfluid,whereastheoutsidehotair andcoldwaterarecalleda heatbath or reservoir.Wewillalsousethesewordsfrom Chapter 2 onwards.Inthischapter,however,weusethebroaderterm‘environment’ or‘bath’torefertoanyexternal,uncontrollablepartoftheworld,notnecessarily describedbyathermodynamicvariablesuchastemperature.Itwillbecomeclear throughoutthisbookthatthepredictivepowerofthesecondlawcomesfroman efficientdescriptionoftheseuncontrollabledegreesoffreedomaboutwhichwehave onlyverylittleinformation.
Quantumsystemswhicharenotisolatedbutincontactwithabathorenvironmentarecalled open quantumsystems;seeFig. 1.1 forsketches.Conceptually,many differentapproachesexisttodescribethemtheoreticallyandaverypowerfuloneis tomodelthebathitselfasanotherquantumsystemsuchthatthesystem and the bath(whichwesometimesalsocallthe universe)constituteonebigisolatedquantum system.Thisistheoriginofsystem–baththeoryandwewillseebelowthatthisis indeednotanassumption:anyopenquantumsystemcanbeseenasbeingpartofa largerisolatedquantumsystem.
Mathematically,thesystem–bathcompositeisa bipartite quantumsystemdescribedbythetensorproductofthesystemandbathHilbertspace: HS ⊗HB .The dimensionofthatspaceisdim(HS ⊗HB )= dim HS dim HB .Formanyapplications
System–BathTheoriesandtheOriginofNoise 5
thedimensionof HS isverysmall,e.g.dim HS =2 forasinglespin,whereasthe dimensionof HB isoftenverylarge,e.g.dim HB =2NA ,wheretheAvogadronumber NA isoftheorderof 1023.Thedynamicsofthesystemandthebathisgovernedby theHamiltonian HSB = HS ⊗ IB + IS ⊗ HB + VSB .Here, HS and HB denotethe Hamiltonianoftheisolatedsystemorbath,respectively,and VSB denotestheirinteraction.TheysumuptothetotalHamiltonian HSB .Whereasthesystemandbath Hamiltoniancommute(sincetheyliveondifferentHilbertspaces)wehaveingeneral [VSB ,HS ] =0 and [VSB ,HB ] =0.Inthefollowing,wesuppresstensorproductswith theidentityfornotationalsimplicityandwritethesystem–bathHamiltonianas
Forsimplicity,weassumednodriving λt here,butthiswillchangeinlaterchapters. Weremarkthatthetensorproductstructureofthesystem–bathcompositeassumes thesystemandbathtobedistinguishableobjectsandimpliesaparticularchoiceof gaugemadewhenidentifyingwhatisthe‘system’andwhatisthe‘bath’.
Sincethesystem–bathcompositeisisolated,itsglobalstatedescribedbythedensityoperator ρSB (t) evolvesaccordingtotheLiouville–vonNeumannequation(1.1) with H replacedby HSB .Thesystemevolutionisobtainedbytakingthepartialtrace:
Incontrasttotheisolatedcase,theevolutionofanopenquantumsystemissignificantlydifferent.NoneofthefourpointsmentionedinSection 1.1 remaintrue:
(i′) Thetimeevolutionof ρS (t) isnotdescribedbyaunitaryoperator.
(ii′) Theeigenvaluesofthesystemstatechangeintime,i.e.eqn(1.3)isreplacedby
(iii′) Sincetheeigenvaluesof ρS (t) change,thepurityofthestatecanchangetoo.In particular,aninitiallypurestatebecomesmixedingeneral.
(iv′) ThevonNeumannentropyisnolongerconserved.NotethatthevonNeumann entropyofthesystemcanbecomelargerorsmallerduringtheevolution,without violatingthesecondlawofthermodynamics.Thesecondlawstatesonlythat thethermodynamicentropyoftheuniverse,i.e.thesystemandthebath,cannot becomesmallerintime.ItdoesnotimplythatthevonNeumannentropyofthe systemstatecannotdecrease.
Illustrativeexample
Weillustratetheaboveargumentsbyconsideringanassemblyof n interactingspins. Readersunfamiliarwithopenquantumsystemsareinvitedtoexplicitlyfollowthis examplebydoingtheirownnumericsforit.Weassumethatthespinsaredescribed bythefollowingglobalHamiltonian:
HSB = HS + HB + VSB (1.10)
QuantumStochasticProcesses
where σ(i) α (α = x,y,z)arethefamiliarPaulimatricesactingonspin i.Thefirstterm describes n isolatedspinswithenergygap¯hΩ.Thesecondtermdescribestheinteractionbetweentwospinswithcouplingstrength gij .Asoursystemwenowchooseoneof thespins,saythefirst,suchthat HS = hΩσ(1) z /2.ThebathHamiltonianconsequently becomes HB = hΩ n i=2 σ(i) z /2+ h n i=2 j>i gij σ(i) x σ(j) x /2 andtheremainingpart definestheinteractionHamiltonian VSB .Theinitialstateofthesystemandbathis assumedtobedecorrelated:
Inthesimulations,wetake ρS (0)= |+ +|S tobeapurestate.Here, |+ ≡ (|0 + |1 )/√2 denotesacoherentsuperpositionoftheeigenstatesof σz (with σz|0 = −|0 and σz|1 =+|1 ),whichcoincidewiththeenergyeigenstatesof HS .Thebathinstead istakentobeacanonicalequilibrium(Gibbs)ensemblewithrespecttotheinverse temperature β,denotedby
where ZB isthepartitionfunctionofthebath.Therefore,weassumethefollowing situation:previoustotheinitialtimethefirstspinisdecoupledfromtheothersand preparedinasuperpositionofenergyeigenstates.Then,attime t =0 wesuddenly switchontheinteractionwiththebath,whichisassumedtobethermalized. Weaimatanumericalexactsimulationofthesystem–bathdynamicsbasedonthe Liouville–vonNeumannequation(1.1).For n spinsthetotaldensitymatrixaswell astheunitarytimeevolutionoperatorare 2n × 2n matrices.Thisexponentialgrowth insizenecessarilylimitsustoconsideronlyafewspins,preciselyweconsiderseven spinsintotal(i.e.thebathconsistsofsixspins).Notethatoneisofteninterestedina baththatis much largerinsize.Computingtheexactdynamicsofanopenquantum systemthenquicklybecomesimpossible,whichmotivatestheneedforefficientand reliableapproximationschemes.Forthemoment,however,asmallbathsufficesto illustrateourpointsabove.Tocontinuewiththediscussionofourmodel,letuschoose thespin–spininteractions gij randomfromauniformdistributionover [0, 1].Wedo notexplicitlywritedownthevaluesfor gij herebecausethedynamicsarequalitatively similarformostchoices.
Numericalresultsforaninitial(dimensionless)bathtemperatureof βhΩ=10 are showninFig. 1.2.Notethatthisbathtemperatureisrelativelycold,i.e.theenergy gap¯hΩ ofeachsinglespinis10timeslargerthanthetypicalenergy kB T = β 1 of athermalexcitation.Figure 1.2ashowsthetimeevolutionoftheexpectationvalue σ(1) x (t)= tr1{σ(1) x ρS (t)}.Forbettercomparisonwealsoplotitstimeevolutionin thecasethatthespinwasisolated,i.e.for VSB =0 (thingreyline).Theirdifference isquitestriking;inparticular,itisdifficulttorecognizeanystructureorpatternfor theopenquantumsystemcase.Figure 1.2bshowsthepurity,whichdecreasesas expected.Notethattheminimalvalueofthepurityforatwo-levelsystemis 1/2
Figure 1.2cshowstheevolutionofthevonNeumannentropy,whichisnolonger conserved.NotethatthemaximumvalueforthevonNeumannentropyofatwo-level
Fig.1.2 Exemplarytimeevolutionofanopenquantumsystemfora‘cold’bath.Thethin greylinein(a)showsthetimeevolutionofanisolatedsystemwithanidenticalsystemHamiltonian.Thethingreylinein(d)showsthetimeevolutionofthequantumrelativeentropy withrespecttoareferencestate,whichdescribesarefinedequilibriumstateintroducedin Section 1.3
systemisln 2 ≈ 0 7.InFig. 1.2dweshowthetimeevolutionofaquantitythat playsanimportantrolethroughoutthebook.Itisknownasthe quantumrelative entropy,whichisdefinedingeneralas
fortwoarbitrarydensitymatrices ρ and σ.Therelativeentropyisnon-negativeand onlyzeroif ρ = σ.Itcanberegardedasameasureofstatistical‘distance’between ρ and σ;furtherinformationisprovidedinAppendix A.Inparticular,weplot
i.e.thedistancebetweenthereducedsystemstateanditsassociatedGibbsstateatthe inversetemperatureofthebath.Onecouldnaivelyexpectthatthisdifferenceshould becomeverysmallforlongtimesinaccordancewithequilibriumstatisticalmechanics. Thisisnotthecasefortwoimportantreasons.First,abathofonlysixspinsisstill toosmalltoinduceequilibrationofasmallquantumsystem.Second,evenifthebath werelarger,equilibriumstatisticalmechanicsinfactpredictsastate different from theGibbsstate,aswewillexplainindetailinthenextsection.Thetimeevolutionof therelativeentropywithrespecttothisdifferentstateisshownbythethingreyline, whichismuchclosertozerothaneqn(1.17).
Finally,Fig. 1.3 showsthesameplotsasFig. 1.2,butforadifferentinitialtemperatureofthebath.Thistimewechose βhΩ=1,suchthatthethermalexcitationenergies
Fig.1.3 Exemplarytimeevolutionofanopenquantumsystemfora‘hot’bath. arecomparablewiththeenergygapofeachsinglespin.Equivalently,onecouldsay thatwehavemore‘noise’inthebath.Thedifferencecomparedwiththecoldcase βhΩ=10 isquitestriking.Oscillationsaremuchlesspronouncedandeqn(1.17)becomesquitesmallaftersometransienttime.Thismeansthatthestandardequilibrium Gibbsensembledescribesthesystemstatequitewell.Infact,thesystemiswelldescribedbyacompletelymixedstate ρS (t) ≈ IS /2,whichfollowsbyconsideringthe timeevolutionofthepurity.
Toconclude,anopenquantumsystembehavesverydifferentlyfromanisolated quantumsystem.Evenforaverysmallbathofonlysixspinseffectssuchasequilibrationandthermalizationstarttobecomevisible.Next,weconsiderequilibriumstates ofopenquantumsystemsinthecasethatthebathismuchlarger.
1.3 EquilibriumStatesofOpenQuantumSystems
Beforeweanalyseequilibriumstatesofopenquantumsystems,itmightbeworth askingwhetheranopenquantumsystemcanactuallyreachanequilibriumstate. Infact,wehaveintroducedopenquantumsystemsviathesystem–bathparadigm, i.e.acompositesystemthatevolvesunitarilyintime.Thisimpliesthat,aslong asthesystem–bathcompositecanbedescribedbyafinite-dimensionalHilbertspace, thedynamicsis quasi-periodic.Bythiswemeanthefollowing.Let |ψ(0) denote theinitialstateofanarbitraryisolatedsystem,whichishereassumedtobepure forsimplicity.WedenotetheeigenvaluesandeigenstatesofitsHamiltonian H by En and |n ,respectively.Then,ifweexpandtheinitialstateas |ψ(0) = n cn|n with complexcoefficients cn obeying n |cn|2 =1,wecanwritethestateattime t as
EquilibriumStatesofOpenQuantumSystems 9
i.e.itisasumofperiodicfunctionswithfrequencies ωn ≡ En/h.Ifwewaitlong enough,wemightwonderwhetherthereexistssometime t andasetofnaturalnumbers {kn} suchthat ωnt =2πkn forall n.Thiswouldthenimplythat ψ(0)|ψ(t) =1,i.e. thesystemreturnedbacktoitsinitialstate.Ifallfrequenciesarerationalnumbers,we canstraightforwardlyfindsuchatime t.Byassumptionwecanthenwrite ωn = qn/rn forsome qn ∈ N and rn ∈ N.Inparticular,ifwedefine N ≡ n rn,wecanwrite ωn = mn/N forall n andsome mn ∈ N.Thus,bychoosing t =2πkN ,weobtain ψ(0)|ψ(t) =1 forall k ∈ N,i.e.thequantumsystemreturnsinfinitelyoftentoits initialstate.
Thingsstarttobecomemoresubtleiftheratio ωn/ωn′ ofsomepairoffrequencies becomes irrational.Indeed,itthenneverhappensthat ψ(0)|ψ(t) =1.However, irrationalnumberscanbeapproximatedarbitrarilywellbyrationalnumbers.Hence, itseemsreasonabletoexpectfromtheforegoingargumentthatthesystemreturns afterasufficientlylongtimetoitsinitialstateuptoa verysmallerror.Indeed,onecan provethatanisolatedfinite-dimensionalquantumsystemreturnsarbitrarilycloseto itsinitialstateinfinitelyoften,i.e.forany ϵ> 0 thereexistinfinitelymanytimes t such that | ψ(0)|ψ(t) | =1 ϵ.Thisisknownasquasi-periodicity.Thisresultisalsoknown fromclassicalmechanicsas Poincaré’srecurrencetheorem.Obviously,sincean openquantumsystemisapartofalargerisolatedsystem,thisalsoimpliesthatany openquantumsystemstatereturnsinfinitelyoftenarbitrarilyclosetoitsinitialstate. Thisseemstoimplythatweshouldnotexpectanopenquantumsystemtoequilibrate atallandPoincaré’srecurrencetheoremhasplayedanimportanthistoricalrolein thedebateonwhetheritispossibletoderivethelawsofthermodynamicsfroman underlyingmicroscopicperspective:Ifallstatesreturnarbitrarilyclosetotheirinitial state,whydoweobserveanyirreversibility?
Thekeyinsighttoresolvethisquestionliesinthefactthatthenexttime t forwhich | ψ(0)|ψ(t) | =1 ϵ happensgrowsincrediblyfastwiththenumberofcoefficients cn in eqn(1.18).Thisnumberisexpectedtoscalewiththenumberofparticlesinthesystem becauseitisexperimentallyextremelyunlikelytoprepareamany-bodysystemina state |ψ(0) ,whichcontainsonlyafewenergyeigenstates |n .Then,iftheisolated systemiscomposedof N particles,e.g.the N spinsinthepreviousexample,one genericallyexpectstheaveragerecurrencetimetoscale doubleexponentially with N , i.e. t = O{exp[exp(N )]}.Ifoneassumesthatthenumberofparticlesistypicallyofthe orderof 1023,theproblemofPoincarérecurrencesbecomesirrelevantforallhuman timescales.
Therefore,weassumefornowthatthesystemequilibratesandreachesastationary statelimt→∞ ρS (t),wherethenotation t →∞ meansthatweconsidertimesmuch largerthantypicaltimescalesoftheopensystemevolution,butstill,ofcourse,smaller thanthePoincarérecurrencetime.Thenextquestionisthen:Whatistheequilibrium stateoftheopenquantumsystem?Findingacompleteanswertothatquestionturns outtobedifficultandisstillthesubjectofintenseresearch.Sincethisisnotthe topicofthebook,wehererestrictourselvestoinvokingargumentsfromequilibrium statisticalmechanics,whichworkwellinmanycases.
Forthispurpose,weconsiderthefamiliar Gibbsstate or canonicalensemble, definedforanysystemwithHamiltonian H by
QuantumStochasticProcesses
Here, β =(kB T ) 1 istheinversetemperatureand Z isthepartitionfunction.Ifthe internalenergy U = tr{Hπ} isfixed,theGibbsstateischaracterizedbythefactthatit maximizesthevonNeumannentropywiththeinversetemperatureimplicitlydefined throughtherelation U = ∂β ln Z.Viceversa,forafixedvonNeumannentropy SvN(π),theGibbsstateminimizestheenergywiththeinversetemperatureimplicitly definedthroughtherelation SvN(π)= β2∂β (β 1 ln Z)
Now,supposethatthesystem–bathcompositeiswelldescribedbyaglobalGibbs state πSB = e βHSB /ZSB with ZSB ≡ trSB {e βHSB }.Whatdoesthereducedsystem statetrB {πSB } looklike?Perhapssurprisingly,itturnsoutthatingeneraltrB {πSB } = πS = e βHS /ZS .Onlyinthecaseofveryweakcouplingbetweenthesystemandthe bath,i.e.if VSB isnegligiblecomparedwith HS and HB ,doesthereducedsystemstate equaltheconventionalcanonicalensemble.Fornon-negligiblecoupling VSB ,however, wedefine π∗ S ≡ trB {πSB } andwehave π∗ S = πS
Nevertheless,itisstillpossibletowrite π∗ S inan apparent Gibbsformwithrespect toan effective Hamiltonian HS :
∗ S =
Infact,thisispossibleforeverydensitymatrix ρS bydefining ˜ HS ≡−β 1 ln( ˜ ZS ρS ), andnotonlyfor π∗ S .Noticethat HS isfixedonlyuptoanarbitrarychoiceofthe positivenormalizationconstant ZS .Forthereducedstate π∗ S ofacanonicalequilibrium ensemblethereisoneconvenientchoicefortheeffectivepartitionfunction,whichwe denoteby Z∗ S = ZS andwhichisobtainedbysetting
Thatis,theeffectivepartitionfunction Z∗ S istheratioofthepartitionfunctionsofthe system–bathcompositeandofthebath alone.ThecorrespondingeffectiveHamiltonian isknownasthe Hamiltonianofmeanforce andreadsexplicitly
OnequicklyverifiesthattrB {
S .TheHamiltonianofmeanforceprovidesaneatconceptusedvarioustimesinthefollowingchapters.Physicallyspeaking, itcanbeseenasaneffectivefreeenergylandscapeforthesystem,aclaimthatbecomes clearerinChapter 2.NoticethattheHamiltonianofmeanforcedependsexplicitlyon theinversetemperature β.Forweakcoupling VSB , H∗ S reducesto HS .Thus,the familiarcanonicalensembleonlyemergesintheweakcouplingregime. Itisnaturaltoask:DoestheeffectiveGibbsstate(1.20)representagoodapproximationoftheequilibratedopenquantumsystemstate,i.e.is π∗ S ≈ limt→∞ ρS (t)?
EquilibriumStatesofOpenQuantumSystems 11
Ifthatisthecase,wesaythatthesystem thermalizes,whichisastrongerrequirementthanequilibrationalone,whichonlyassumesthesystemstatetobecometime independentforlongtimes.ParallelingtheobjectionsraisedbyPoincaré’srecurrence theoremabovethatequilibrationcanneverstrictlyhappen,similardoubtsmayrisefor thecaseofthermalization.Inparticular,noinitialsystem–bathstate ρSB (0) different from πSB willeverreachthelatterstateduringtheevolution.
Exercise1.1 Showthat,if ρSB (0) = πSB andif HSB istimeindependent, ρSB (t) = πSB forall t
However,similartothecaseofequilibration,thermalizationshouldalsoberegardedasaconvenient illusion byrecallingthatourexperimentalcapabilitiesare limited.Forabathwithitsprosaic 1023 degreesoffreedom,thefullsystem–bathstate ρSB (t),whichisdefinedonaHilbertspaceofdimensionoftheorderof 101023 ,remains experimentallyinaccessible.Instead,onetypicallyhasaccessonlytoarestrictedset ofobservables,forinstancethosedeterminedbylookingattheopenquantumsystem. Thermalizationtoeqn(1.20)isthenverylikelytohappenaslongasonecanmeaningfullyassociatesomemacroscopictemperature T withthebath.Exceptionsare,for instance,abathconsistingoftwopartskeptatdifferenttemperatures(ascenariothat becomesrelevantinlaterchapterswhenstudyingtransportprocesses)orabathpreparedinagiantSchrödingercatstateasasuperpositionoftwoverydifferentenergies (anunlikelyscenario).Furthermore,alsointhepresenceofadditionalconservation laws,i.e.ifsomeobservablescommutewiththeglobalHamiltonian,thermalization toeqn(1.20)willtypicallynothappen.However,ifthesescenarioscanbeexcluded, manyopenquantumsystemsthermalizetoeqn(1.20)regardlessoftheinitialstate ρS (0).Infact,thisobservationisconfirmedbyourexampleattheendofSection 1.2 ThegreylineinFigs. 1.2dand 1.3dshowsthetimeevolutionof D[ρS (t)|π∗ S ].Wesee that,evenforabathofonlysixspins, π∗ S canrepresentagoodapproximationto theopensystemstate,evenatlowtemperatures,i.e.intheregimewherequantum fluctuationsdominatethermalfluctuations.
Thelastobservationraisesthequestionofwhetherthedeviationof π∗ S fromthe standardGibbsstate πS ismainlycausedbyquantumeffects.Ingeneral,thisdoesnot needtobethecase,butwewillreturntothisquestionmorerigorouslyinSection 3.6 whenwediscussthezerothlawofthermodynamics.Fornow,weconcludethissection bystudyinganimportantclassofmodelsforwhichthereisacleardifferencebetween π∗ S and πS inthequantumandclassicalregime.
Exercise1.2 Consideraharmonicoscillatorwithfrequency ω andHamiltonian(inmassweightedcoordinates) HS = 1 2 (p 2 S +ω 2 x 2 S ) coupledtoa‘bath’ofoneotherharmonicoscillator withthesamefrequency ω.TheglobalHamiltonianis
Here,thecouplingstrengthis c andwehavewrittentheHamiltonianinamanifestlypositive formsuchthat HSB ≥ 0 foranychoiceof ω and c.Now,showfirstthat,iftreatedasaclassical system,thereisnocorrectiontothethermalstateofthesystem: π
S /ZS . Hint:















