Introduction
Allthestudiesoflightfromtheantiquityuntilthemiddleofnineteenthcenturywerebased onincoherentlightsourcessuchastheSun,candlelight,sodiumlamp,orlightbulb.In1950s anewcoherentsourceoflightwasinvented,firstinthemicrowaveregionandtheninthe opticalregion.Thisnewkindoflightsource,thelaser,isoneofthegreatestinventionsofthe secondpartofthetwentiethcentury.Ithashelpedtorevolutionizemanybranchesofscience andtechnology,rangingfrombiotechnologyandprecisionmeasurementstocommunication andremotesensing.ANobelPrizewasawardedin1964fortheinventionofthelaserandsince thensome10additionalprizeshavebeenawardedinvolvingthistechnology.
Thephysicalprocessbehindconventionallightsourcesisspontaneousemissionandthe sourceoperatesinthermalequilibrium.Initially,themajorityofatomsandmoleculesarein theirgroundstate.Whenenergyissuppliedtotheatomsormolecules,someofthemgotothe excitedstatesandthenradiateviaspontaneousemission.Thespontaneousemissionprocess isduetotheubiquitousvacuumfluctuations1andeachatomradiatesindependentlyofeach other.Theresultinglightisawhitelightsentinalldirectionsandisincoherent.Ontheother hand,thedominantemissionprocessinalaserisstimulatedemission.Byacleverdesign,the radiatedphotonsbytheatomsormoleculesareabletostimulateotheratomstoradiatewiththe samefrequencyandsamedirection.Theresultingradiationiscoherent,i.e.,monochromatic, andhighlydirectional.
Inthistextwewanttolookatopticalscienceusingthefactthattheencounterofcoherent lightisprobableratherthanimprobable.Wewillviewlightasanelectromagneticwave describedcompletelybyMaxwell’sequations.Thisisasetofvectorequationsbutwewilldo ourbesttolimitourdiscussiontoscalar,one-dimensionalwaves.Weonlywillusevectors wherewemusttocharacterizethepropertiesofalightwavesuchasthefactthatsolutionsof Maxwell’sequationsaresolutionsofawaveequationconcealedwithinMaxwell’sequations. Theamplitudeoftheelectricandmagneticwavesthatmakeupalightwaveareorthogonalto thedirectionofpropagationandtoeachother.Wewillintroducethemethodusedtohandlethe vectornatureofthewave’sdisplacementvectorsusingthetheoryofpolarization.
Wemustalsousevectorstodiscussreflectionandrefractionsincethemagnitudeofthe wavethatundergoesreflectiondependsontheorientationoftheelectricfielddisplacement. Weareabletoprovethatinterferencerequiresthatthepolarizationofthewavesparticipating ininterferencemustbeparallel.Thisallowsustolimitdiscussionstoscalarwaves.
Interferenceandcoherencearetreatedtogether.Thesearethekeystoourmodernviewof opticsbasedonFouriertheory.BecauseFouriertheoryisthebasisforourmoderndescription ofdiffractionandimaging,wespendalittletimedescribingthetheorybutwelimitour discussiontoverysimplefunctionssuchasarectangle.
1 Thisisthetemporarychangeintheenergyatapointinspace.
Therearesometopicsdiscussedinthebookthatcanbeskippedbecauseoftheiradvanced nature.Theyhavebeenindicatedbytealboxessettingofftheparagraphscontainingthe advancedmaterial.Theinstructorcandecide,astheclassprogresses,whethertoincludethe material.
Interferenceisonlyobservediftheinterferingwavesarecoherentandifthepolarization ofthewavesisparallel.Thepresenceofcoherenceallowsanumberofusefulexperimental techniquestobeused,suchasthequalityofopticalcomponentsusingNewton’sringsora Michelsoninterferometer;useofaMichelsoninterferometerandFouriertransformsmakes itpossibletoevaluatethespectrumofasource.Byusingasourcewithaknownspectral distribution,itispossibletocreateanopticalcoherencetomographicthree-dimensionalimage ofbiologicalmaterial,suchastheretinaorthecorneaofthehumaneye.Aninterferometer basedonYoung’stwo-slitexperimentcanbeusedtomeasurethesizeofstellarobjects.Finally, interferencegeneratedbydielectriclayerscanbeusedtoreducethereflectionsfromthesurface ofopticalcomponentsforcomplexcameralensesorhighindexeyeglasses.
Anumberofdifferenttheoriesarebasedonwavetheorybutmostofthemassumeascalar wave;i.e.,theamplitudeofthewaveisascalarfunction.Light,however,isanelectromagnetic wavewiththewavedisplacementdescribedbyamagneticandanelectricvector.Wecan describethevectorwaveintermsofonlytheelectricfieldvector.Inthisbookweoutlinethe mathusedtodescribethevectornatureofthewaveintermsofitspolarizationanddiscuss opticaldevicesusedtoexperimentallymanipulatethepolarizationvector.Thepolarizationof lightisaffectedbychemicalcompoundspossessingopticalactivity;thechiralpropertyanda briefintroductiontothatpropertyisgiven.
Inmanyopticstextbooks,emphasisisplacedonthethinlensequation,andsimpleoptical systemsinvolveoftennomorethanoneelement.Thisisoflittleusetothestudentsincesingle opticalelementsaredominatedbyaberrationsandinthelabacombinationofatleasttwo lenseswouldbepreferredtoeliminatesphericalaberration.Wehaveintroducedthestudentto themathneededtohandlemultipleopticalcomponentsandselectedasignconventionbased onthatusedinaCartesiancoordinatesystemthatdoesnotresultinutterconfusionwhen multipleelementsaretreated.Actualopticaldesigniscomplicatedandhardtodowell.For thatreason,aberrationsandtheirexamplesareonlydescribedandexperimentallyobtained examplesshown.
Triggeredbythedevelopmentoflasers,anewmethodofcommunicationsbasedonthe useofopticalfiberswasdevelopedinthe1970s.Whenapropagatinglightwaveencountersa barrierbetweenahighindexofrefractionmaterialandamaterialwithlowindexofrefraction, wecanobservetotalreflection.Ifalightwaveisconfinedtothehighindexdielectricmedium bythetotalreflection,thelightcanpropagatelongdistanceswithoutattenuationandcanbe madetocarrylargequantitiesofinformation.Beginningabout2010theabilitytoconduct communicationswithoutconversionfromtheopticalregimemadeitpossibletostreammovies andsportingevents,causingarapidexpansionofopticalfibertechnology.Weexplorethe descriptionoffiberopticalsystemsbasedonageometricalmodelcalledthezig-zagtheory.
Becauseitiseasytoconstructcoherentlightsourcesitiseasytoseetheinterferenceof multiplewavesscatteredfromcomplicatedstructures.Thishasledtotheinventionofthe previouslymentionedopticalcoherencetomographymicroscopeofretinalimaging.Thisis anextensionoftheconceptofinterferenceintoamuchmorecomplicatedtheorywhichisonly
mentionedinpassinginthistext.Wehavefounditpossibletoderivesimplemathematical expressionsthatmakeitpossibletocalculatediffractionfromsimplegeometricconstructs.The theoryallowsustobuildatheorythatcanbeusedtopredictlimitstoourimagingcapability. Thetheorymakesitpossibletocomparethecapabilitiesofavarietyofimagingsystems,such ascellphonecameras.Italsoallowsustodevelopwayofprocessingimagerythatpermits,for example,theextractionoftheimageofaplanetorbitingadistantstar.
1 Waves
1.1 WaveParameters
Thebasiccharacteroflightisexplainedusingthetheoryofwavemotion.Mathematically,a waveisthesolutionofasecond-order,partialdifferentialequationcalledthewaveequation. Thesolutionisviewedasanoscillationthattransfersenergyfromonepointtoanotherwithout anymassflow.Inonedimension,theequationofascalarwavepropagatingwithoutchangein the x-directionhastheform
where c isthevelocityofthewave.Thisdifferentialequationcanbeusedtodescribeanumber ofphysicalsituations:avibratingguitarstring,soundwaves,avibratingdrumhead,elastic wavesinsolidssuchasseismicwavesintheearth,oceanwaves,electricsignalsinacable,and electromagneticwaves—viz.alightwavethatisofinteresttous.
Theideathatsoundwasawavecamefromobservingwaterwavesandwasintroduced around240bcbytheGreekphilosopherChrysippus.Pythagoras,theancientGreekphilosopherandmathematician,studiedthevibrationofstringsaround500bc.Theconnection betweentheproductionofsoundbyvibratingbellsorstringsandsoundwavesinairwasmade byGalileo.Gassendi,acontemporaryofGalileo,arguedforaparticleviewofthepropagation ofsound.
DanielBernoulli,aSwissmathematician,triedtodevelopanunderstandingofhowaviolin stringmadesound.Inthe1720s,hedevelopedawayofdescribingastringasitvibrated byimaginingthestringascomposedoftinymasses,connectedbysprings.ApplyingIsaac Newton’slawsofmotionfortheindividualmassesallowedBernoullitopredictthatthesimplest shapeofavibratingviolinstring,fixedateachend,wasasinglesinecurve.Somedecadeslater, mathematicianJeanLeRondd’Alembertgeneralizedthestringproblemintoamathematical expressionofthewaveequation.Hefoundthattheaccelerationofanysegmentofthestringwas proportionaltothetensionactingonit.Thewavescreatedbydifferenttensionsofthestring producedifferentnotes.Withthistheoreticaldevelopment,thedesignofstringinstruments becamepossible.
Thesuccessofthetreatmentofsoundwavessuggestedtoscientistsoftheearlyseventeenth centurythattheyshouldviewtheuniverseasalargemechanicaldeviceandtoapplya mechanicalmodeltoallobservables,evenlight.Everythingwasmadeofmatterandmotion. Matterwasmadeupofatomsthatwereindivisible.Corpuscleswerelargerparticleswith propertiesthatcontrolledtheirfunctionandtheyactedasvehicles,carryingstuffthrough
ModernOpticsSimplified.B.D.Guenther.©B.D.Guenther2020. Publishedin2020byOxfordUniversityPress.DOI:10.1093/oso/9780198842859.001.0001
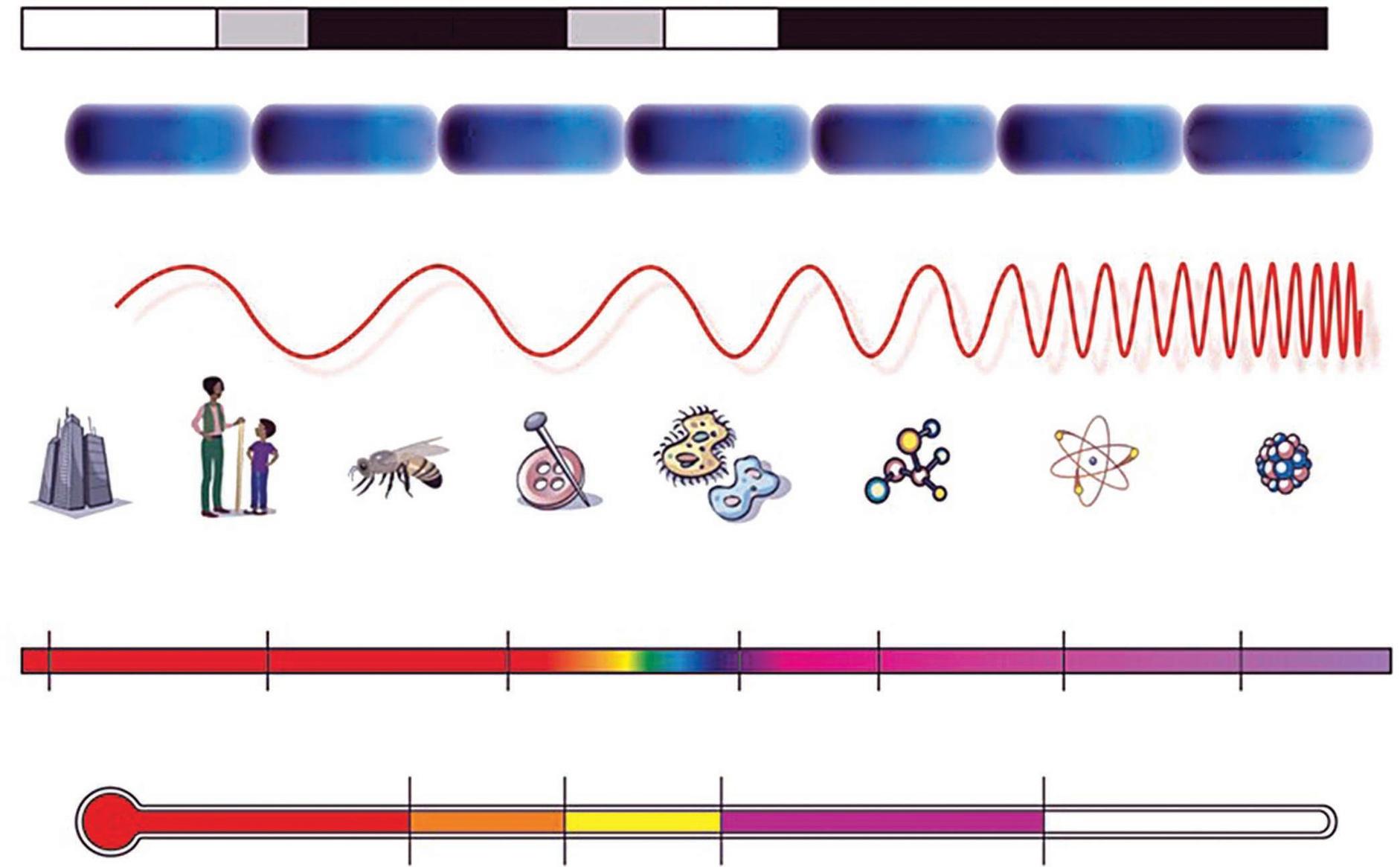
Penetrates Earth Atmosphere?
THE ELECTROMAGNETIC SPECTRUM
Figure1.1 Frequencyregionsoftheelectromagneticspectrum.Thetheoriesdiscussedinthetextcoverthe frequenciesfrom1012 to1016 Hz.
ByNASA [Publicdomain],viaWikimediaCommons.
space.RenéDescartesdescribedlightasapressurewavetransmittingataninfinitespeed throughsometypeofelasticmedium.
ChristiaanHuygensin1672developedamathematicalwavetheoryoflight.Heretaineda mechanicalviewoflightbyrequiringthewavetotravelina luminiferousether.IsaacNewton latchedontotheparticle(corpuscle)theoryofGassenditobuildhisparticletheoryoflight.He rejectedtheconceptofwavepropagationbecauselightseemedtotravelinastraightline.The weaknessofhistheorywasthatitexplainedrefractionbyassumingthatlighttraveledfasterina densematerial,oppositetothepredictionsofHuygens’stheory.Newton’stheorywasdominant throughouttheeighteeenthcentury.
In1800,ThomasYoungdemonstratedthroughdiffractionexperimentsusingtwoslitsthat lightbehavedasawave.In1817Augustin-JeanFresnelworkedoutawavetheoryoflightthat helpedcastNewton’stheoryinpoorlight.Itwasnotuntilpropagationvelocitymeasurements madebyLéonFoucaultin1850demonstratedthatthepropagationvelocityinadensemedium waslessthaninavacuum.Withthisexperimentalevidence,Newton’sparticletheorywas abandoned.
Theneedtoexplainlightresultedinthedevelopmentofatheoryofelectromagneticwavesby JamesClerkMaxwellin1862.Electromagneticwaveshavefrequenciesthatextendovermany ordersofmagnitude(seeFigure1.1).
Wewilldeveloptheparametersusedtoidentifyawaveinthischapter.Wewilldiscuss Maxwell’sequationsthatexplainthebehavioroftheelectromagneticspectrumofFigure1.1in thenextchapter.
ThewavemustbeasolutionofEq.(1.1);i.e.,itisafunctionoftwovariables:aspatialvariable andatemporalvariable:
y ≡ f(x,t)
Tomaketheproblemassimpleaspossible,wewillassumethatawavepropagatesinour medium(currentlyundefined)withoutchange.Ifthewavepropagatesbetween x1 and x2,then thewavefunctionevaluatedat(x1, t1)musthavethesamevalueasat(x2, t2).Thevelocityof propagationalongthe x-directioninourmediumisequalto c andthevelocityallowsusto calculatethenewpositionofthewavefromtheoldpositionusingtheequation
x2 = x1 + c(t2 t1)
Onewaytosatisfytherequirementofpropagationwithoutchangeistoassumethewave functionhastheform1
y = f(ct x). (1.2)
Itiseasytoshowthisfunctionalformmeetsourrequirement
Toourrequirementofpropagationwithoutchange,weaddasecondrequirementthateach pointonthewaveoscillatetransversely,i.e.,perpendiculartothedirectionofpropagation,with simpleharmonicmotion.Agoodphysicalexampleofsuchawavewouldbeaguitarstring vibratingatitsfundamentalfrequency—forexample,thefifthguitarstring(A)vibratingat 110Hz.Theequationsofmotionofapointonthewavevibratingwithsimpleharmonicmotion isgivenby
m d2x dt2 + sx = 0. (1.3)
Thepointonlymovestransverselytothewavemotion.Whenthesignofthe x and t componentsofthewavephasediffer,thewavetravelsinthepositive x-direction.Thepointonthe wave,havingbeendisplaced,experiencesalinearrestoringforcethatdefines s andisgivenby
F =−sx = ma = m d2x dt2 .
Theconstantsiscalledthespringconstant.
Itwouldappearthatsuchasimple,second-order,differentialequationwouldhavelimited applicability,butsuchisnotthecase.Theforceactinguponamasscanbewritteninterms ofthepotentialenergyfunction, V,
F =− dV dx .
Thepotentialfunctionisusedbecauseitisascalarandthuseasiertomanipulatethana vector.Weseethatourforce F =−sx isduetoapotentialenergyfunction V(x)thatis
1 Theexpression y = f(ct x)isshorthandnotationtodenoteafunctionthatcontains x and t onlyinthe combination(ct x);i.e.,thefunctioncancontaincombinationsoftheform2(ct x),(t ± x/c),(x ct), (ct x)2,sin(ct x),etc.,butnotexpressionssuchas(2ct x)or(ct2 x2).
proportionalto x2.Ifwehaveamorecomplicatedpotentialfunction,wecanexpandthe potentialfunction,abouttheequilibriumpoint,inaTaylorseries V = V0 + 1 2 (d2V dx2 )x2 + 1 6 (d3V dx3 )x3 +....
Thereisnoterminvolving x,because V(x)isaminimumattheequilibriumpositionand thederivativeiszero.WeseeourmodelisapplicablewhentheTaylorexpansionbeyond thefirstnon-zerotermisnotneeded,i.e.,whenthedisplacements, x,oftheoscillations abouttheequilibriumpositionaresmall.
ThesolutionofEquationEq.(1.3)is
where �� issetbytheinitialconditions.Ifweassumethattheamplitudeofdisplacementis A at t = 0,then ��= 0.
Wecanusethisharmonicmotiontodefineseveralwaveparameters:
• The period, T,isthetimerequiredtocompleteoneoscillation.Thevalueof x attime t and (t + T)mustbeequal;thus,thetwophasesdifferby2��:
• Thefrequencyofoscillation,i.e.,thenumberoftimesxhasthesamevalueinaunitoftime, isthereciprocaloftheperiod
Weusetheangularfrequencytokeepfromcontinuallywriting2�� inourequations: ��= 2��v.
Usingourassumptionsofthepropertiesofthewave’samplitude,wecanwritethefunctionof (ct x),whichwillreducetoharmonicmotionat x = 0,as
y = f(ct x)= Ycos[�� c (ct x)]
Thisiscalleda harmonicwave. Wewillnowaddanotherparameterthatwewillusetocharacterizeawave;itiscalledthe propagationconstant orthe wavenumber:
Thisisthespatialfrequencyofthewaveandismeasuredinthenumberofwavesperunit distanceascompairedtothetemporalfrequency,��,whichisequaltothenumberofwavesper unittime.Thegeneralizedharmonicwavecanthenbewritten
Thevaluesof x,with t fixed,forwhichthephase(��t kx)changesby2�� isthe spatialperiod andiscalledthe wavelength, ��.Let x2 = x1 +��,sothat
Thus,
(1.9)
Thefinalparameterwewouldliketodefineforourwaveisitspropagationvelocity.To determinethespeedofthewaveinspace,apointonthewaveisselectedandthetimeittakes togosomedistanceismeasured.Thisisequivalenttoaskinghowfastagivenvalueofphase propagatesinspace.AssumethatinthetimeΔt =(t2 – t1)thedisturbance y1 travelsadistance Δx =(x2 – x1).Sincethedisturbanceatthetwopointsisthesame,i.e.,y1,thenthephasesmust beequal:
t kx =��(t +Δt) k(x +Δx), Δx Δt = �� k .
Inthelimitas Δt → 0,weobtainthe phasevelocity
c ≡ dx dt = �� k ; since k =��/c = 2����/c,wealsohavetherelationshipbetweenwavelength,frequency,and propagationvelocity, c =����.2
DimensionalRepresentation
Wenowhavedefinedparametersthatcanbeusedtocharacterizeanarbitrarywavebut onlyinonedimension.Weknowthatlighttravelsinathree-dimensionalspace.What changestotheparameterswillbenecessarytodescribethewaveinthreedimensions?
Thewaveequation,generalizedtothreedimensions,becomes
2 Anotherwaytodeterminethephasevelocityistousearesultfrompartialdifferentialcalculus
Thisrelationshipisusefulevenwithoutknowledgeofisorigin.
Orusingvectorcalculusnotation,wecanwriteEq.(1.10)intermsofthedel(nabla, ∇) operator: ∇2f(r,t)= 1 c2 ��2f(r,t) ��t2
InCartesiancoordinates
iscalledtheLaplaceoperatorandisthedivergenceofafunction’sgradient.Ageneralized harmonicwavesolutionofEq.(1.11)is
f(r,t)= E(r)cos[��t −��(r)]
wherewehavereplaced kx inEq.(1.8)byasurfacedescribedby��(r).Thisqualitydefines asurfaceoverwhich ��(r) = constantatafixedtime.Thatsurfaceiscallthe wavefront.If thesurfacedefinedby ��(r)isaplanewithaunitvector, n, normaltoitssurface(inthree dimensions,theunitvectornormaltoapointinaplaneisthedefinitionoftheplane), then r •̂ n = s definestheplanelocatedadistance r fromtheorigin.
Wewilllimitmostofourdiscussionsinthistexttowaveswithaplanewavefront (Figure1.2).If ��(r)describesaplanewavethenitmustbegivenby ��(r)= k(n • r)
Wedefinethewavevectoras
Figure1.2 (a)Aplanewave.Itsnormalistheunitvector n thatpointsinthedirectionofpropagation.Asurface ofconstantphaseistheshadedplanepassingthroughthepointdefinedbythevector r.(b)Theprojectionof r on theplane’snormaldefinesthedistance s fromtheorigin.
andtheplanewavesolutionsofthewaveequationin3Dbecome
Themanipulationofsinesandcosinesplacesademandonustorememberavariety oftrigonometricidentities.Wecanremovethatunreasonabledemandbyusingcomplex notation.Thegeneralizedsolutionofthewaveequationcanbeexpressedincomplex notation,usingEuler’stheorem
Theamplitude E (r)canbecomplexandcontainanarbitralphaseterm. Ifwesubstitute f(r,t)intothewaveequationEq.(1.11),weobtain
Usingtherelationship ��/c = k,thewaveequationbecomes
Ifweareinterestedinthespatialpropertiesofthewavebutnotthetemporal,weneed onlyseeksolutionsofthisequation,whichiscalledthe Helmholtzequation.
Useofthecomplexnotationwillsimplifyourcalculationsinvolvingwaves.Theonly requirementthatmustbemetthenistoremembertoretainonlytherealpartofthe solutionwhenwecompleteouranalysis.IfouranalysisyieldsEq.(1.13),thenthesolution wewillretainis
Re{f(r,t)}= E (r)cos(��t k • r)
Thisresultfollowsfrom
1.2 FourierTheory
Aquestionprobablyhasariseninthereader’smindastohowageneraltheoryofoptics canbedevelopedusingonlyasinglecosinerepresentationofaplanewave. JeanBaptiste JosephBarondeFourier(1768–1830) developedatechniquetomakeitpossibletosolveheat flowproblems.Thistheorymakesitpossibletoutilizeplaneharmonicwavestoconstructa
descriptionofanygeneralwaveform.Fourier’sfirstpaperonthesubjectwasrejectedbecause Lagrangedidnotbelievetheserieswouldconverge.Intheeighteenthcentury,mathematicians didnotconsideritpossiblethatafinitefunctioncouldcontainaninfiniteseriesofterms. ThelackofunderstandingaboutconvergenceofinfiniteseriesishighlightedbyoneofZeno’s paradoxes:
Achilleswastoraceatortoiseandthetortoisewasgivenalead.Theargumentwasmadethat Achillescouldnevercatchthetortoisebecausehefirsthadtoreachthepointwherethetortoise startedbutbythenthetortoisehadmovedahead.NomatterhowfastAchillesran,thetortoise addedafinitedistancetotheseparationthatallowedhimtoremainaheadofAchilles.
Theunstatedassumptionwasthatthesumofaninfiniteseriescouldn’tbefinite.Thesolution tothisparadoxwasfoundindevelopingawaytodeterminewhetheraseriesconverged.Inthis particularproblemifAchillescutsthedistancetothetortoiseinhalfineachintervaloftime, hecatchesthetortoise.ThedistanceAchillestraversesisgivenby
OurcurrentunderstandingofconvergencehaseliminatedZeno’sparadoxformathematicians andanyuncertaintyofthecorrectnessofFouriertheory.
1.2.1 Fouriertheoryforperiodicfunctions
Fouriertheorystatesthatanyperiodicfunctions, f(t)= f(t + T), where T istheperiod,can bedescribedasumofsinusoidalfunctionscalledtheFourierseries,
Thereisasetofcriteriathat f(t)mustmeetfortheexpansiontobecorrect.3Functionsthat donotmeetthesecriteriacanbeconstructed,butexperimentallytheconditionsarealmost alwaysmet.Tounderstandtheseequationsletusexplorethedescriptionofaperiodicsetof rectangularpulses:
where T = 2��/�� istheperiodofthewave.Theconstant q inEq.(1.17)allowsustovarythe widthofthepositive-goingpartoftherectangularwaverelativetotheperiod.Thisparameter canbevariedtoincreasethedurationoftheperiod.
ByproperlyselectingtheoriginwecansimplifyourcalculationsoftheFourierseries byforcingthefunctiontobeevenorodd.Aneven(odd)functioncanbedescribedbya singlecosine(sine)seriesmadeupofharmonicsofthefundamentalfrequencyoftheperiodic function.InFigure1.3wehavesettheoriginsothatoursquarewaveisanevenfunctionand sotheFourierserieswillinvolveonlycosineharmonics.
Figure1.3 Generalizedsquarewavewhere q isaconstant.Thedurationofthepositiveportionofthesquarewaveis inverselyrelatedtothesizeof q.Theuseof q allowsustovarytheperiodofthefunction.
3 DirichletconditionsformasufficientconditionforthedescriptionofaperiodicfunctionbyitsFourierseries. Therequirementsarethatfmust:
• besinglevalued,
• haveafinitenumberofmaximaandminimainanyfiniteinterval,
• haveafinitenumberoffinitediscontinuitiesbuttheycannotbeinfinite,and
• leadtoafinitefrequencyspectrum.
Toclarifythestatementaboutevenandoddfunctions,suppose f isanevenfunction
f(t)= f( t),
then f(t)willberepresentedbyaseriesofcosines.Thisoccursbecausetheintegralover oneperiod,aboutzero(from −��/�� to ��/��),ofanevenfunctionisnonzero.Theintegral ofanoddfunctionoverthesameintervaliszero.Usingthisfactwecandeterminethat Eq.(1.16)willbezerowheneverf(t)isanevenfunctionbecausethesineisanoddfunction andtheproductofanoddfunctionandanevenfunctionisanoddfunction.
If f(t)isanoddfunction
f(t)=−f( t),
thenitcanberepresentedbyaseriesofsinetermsbecausetheproductof f(t)andthe sineiseven.If f(t)isneitheroddnoreven(forexample, f(t)= et),thenboththesineand cosineseriesarerequired.
ThecalculationisalittlesimplerifweusecomplexnotationfortheFourierseries.Using theidentities
theFourierseriesisthen
ThecoefficientsoftheseriescanbeobtainedbyevaluatingtheintegralEq.(1.20).Forthe squarewave f(t)=1inEq.(1.17)overtheinterval ( T/2 =−��/��)≤t≤(��/��= T/2)
ThefunctioninEq.(1.21)isencounteredsooftenitisgivenitsownname: sinc x = sinx x .
Figure1.4 TheFourierseriesapproximationofasquarewavewiththeseriesterminatedafterthefundamental,third, fifth,andseventhharmonic.
Byincreasing q wecanletthesquarewaveperiodapproachinfinity.Tostart,let q = 4,giving usexactlyasquarewave.Theareaenclosedbythesquarewaveis
(1.22)
WecancombinethepositiveandnegativeexponentsofEq.(1.19)inordertoexpressthe expansionintermsofcosinefunctions.TheFourierseriesbecomes f(t)= 1 2 + 2[cos��t �� cos3��t 3�� + cos5��t 5�� ...].
Wehaveasumofoddharmonicsofthefundamentalfrequencyofthesquarewave.Asweadd termswegetacurveapproachingasquarewaveinFigure1.4.
Anotherwaytorepresentthefunctionisintermsofitspowerspectrum,i.e.aplotofthe coefficientsoftheseries,Eq.(1.21).
ThespectrumshowninFigure1.5ismadeupofasetofdiscretefrequencies.Thewidthof thebarsrepresentingeachfrequencyisexaggeratedtomakeiteasytosee.Asweincrease q,
Figure1.5 Frequencyspectrumofasquarewave,i.e.,thecoefficientsoftheFourierseriesofthesquarewavewhere q = 4.
= 16
Figure1.6 Frequencyspectrumofasquarewaveofwidth T/8.Thelinetracedoverthehistogramaidstheeyein seeingtheapproachofthediscretespectrumtoacontinuouscurveshowninFigure1.7.
theperiodgrowsandthespectrumbecomesafinerandfinersetofdiscretefrequencieswith anenvelopeindicatedbyasmoothcurveshowninFigure1.6.
1.2.2 Non-periodicfunction
Ifwelet q →∞,theperiod T goestoinfinity,creatinganon-periodicsquarepulse.Thisleads ustothedefinitionoftheFouriertransform,definedforanon-periodicfunction, g(t),as
orintermsofsinesandcosines
Letusturnourperiodicsquarewave(1.17)intoasinglepulsebyletting q becomeverylarge; thefunctionthenbecomes f(��)={1 ��≤��0/2
0allother �� .
Nowthespectrumgivenby G(��)isacontinuousdistributionoffrequencies,shownin Figure1.7,ratherthanthediscretedistributionoffrequenciesthatcharacterizeaperiodic function.
1.2.3 SpatialFourierTransforms
Wehavewrittenrelationshipsusingtimeandfrequencybutwecouldreplacetimewithaspace variable,say x.Thetransformorconjugatevariablemusthavereciprocalunits;thus,when aspacevariableisused,theconjugateunitsare“distance”anditsreciprocal,1/“distance”. Theconjugatevariabletothespacevariableiscalled spatialfrequency andinopticsisthe propagationconstant k (remember k = 1/��).Wecanusethespatialfrequenciesforasetof planewavespropagatingoveraspectrumofanglestoconstructapropagatingwavefrontof anyshape.Thismeansasimpletheoryconstructedaroundaharmonicplanewavecanform thebasisforthedescriptionofanypropagatinglightwave.Thismathematicalformulation servesasthefoundationofmodernoptics.Laterwewillestablishaconnectionbetween k and physicalparametersthatwecanmeasureinopticalexperiments.Fornowwewillusetimeand frequencyinourdiscussions.
UncertaintyRelationship
Thereisanimportantrelationship,calledtheGaborlimit,⁴betweentwoconjugate dimensions: ��⟺ t or x ⟺ kx.Theuncertaintyarisesbecausetheconjugatevariables arerelatedviatheFouriertransform.Let’slookatatemporalsignal.Mathematically,we wouldknowthevaluesof f(t)atsometime t0 accuratelyifitiscompact,i.e.if f(t0)iszero beyondsomelimit,asinEq.(1.23)where t0 = 0beyond t =±��0/2.Weknow f(t)withan uncertaintyof ��0.Statedsimply,thetemporalspreadissmall.Thesmallerthetemporal spreadis,themorefrequenciesarerequiredbyFouriertheorytodescribethetemporal signal.Thus,themoreaccuratethetemporalsignalis,smallerΔt ,thelowerthefrequency resolution,larger Δ�� ,wecansimultaneouslystate:
ΔtΔ��≥ 1/2
AnotherwaytostatethisfactisthroughtheuseofthescalingpropertyofaFourier transform:
ℱ{g(at)}= 1 a G( 1 ��).