ModernApplications ofGraphTheory
VADIMZVEROVICH
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries ©VadimZverovich2021
Themoralrightsoftheauthorhavebeenasserted FirstEditionpublishedin2021
Impression:1
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica
BritishLibraryCataloguinginPublicationData Dataavailable
LibraryofCongressControlNumber:2020952669
ISBN978–0–19–885674–0
DOI:10.1093/oso/9780198856740.001.0001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
Tomywife,Svetlana,andourdaughters,AlexandraandKatherine. Hopefully,nottoomanygoodnightkisseshadbeenmissedduringthe completionofthisbook.
3.EmergencyResponse:NavigableNetworksandOptimal RoutinginHazardousIndoorEnvironments 109
3.1AutomatedSelectionofSafestandBalancedRoutes 110
3.1.1TheBuildingInformationModelling–GeographyInformation Science(BIM-GIS)Model 110
3.1.2TestBuildingandTessellationofCorridors 114
3.1.3AlgorithmsforSafestandBalancedRoutes 116
3.1.4TestingtheAlgorithms 127
3.2AnalyticPrioritizationofIndoorRoutesforSearch andRescueOperations 134
3.2.1AlgorithmforPrioritizationofIndoorRoutes(PIR-Algorithm)137
3.2.2TestingPIR-Algorithm 150
3.2.3Incorporating‘Time’intoPIR-Algorithm 155
3.3AutomatedConstructionofVariableDensityNavigableNetworks167
3.3.1MethodologyandtheAlgorithm
3.3.2ResultsandDiscussion
3.3.3ComparisonofVDNwithPrevailingIndoorNavigableNetworks181 3.4RelatedWork
4.GraphModelsforBackboneSetsandLimited PackingsinNetworks 213
4.1MultipleDominationModelsforBackboneSets
4.1.1BasicDefinitionsandKeyKnownResults
4.1.2 k-TupleDomination
4.1.3 k-Domination
4.1.4 α-Dominationand α-RateDomination
4.1.5ComplexityandImplementationoftheAlgorithms
4.2LimitedPackingsinGraphs
4.2.1TheProbabilisticConstructionandLowerBounds
4.2.2RandomizedAlgorithm
4.2.3SharpnessoftheLowerBounds
4.3GeneralizationsofMultipleDomination
4.3.1Frameworkfor ⟨r, s⟩-Domination
4.3.2FrameworkforParametricDomination
4.3.3ThresholdFunctionsforMultipleDomination
4.4Exercises
5.GraphModelsforOptimizationProblemsinRoadNetworks275
5.1PedestrianRoadSafetyinUrbanAreas
5.1.1AutomatedConstructionofPavementNetworks (PNC-Algorithm)
5.1.2SearchforandPrioritizationofPedestrianPaths(PPP-Algorithm)280
5.1.3RelatedWork
5.2PlacementofChargingStationsforElectricVehiclesinRoad Networks
5.2.1ReachabilityGraphandMultipleDominationModels
5.2.3ExperimentalEvaluation
5.2.4MixedIntegerLinearProgramming(MILP)Formulation
6.1ABriefOverviewofGraphModels
6.2GraphsandtheMolecularEvolutionofViruses
Preface
Thisbookdiscussesmanymodern,cutting-edgeapplicationsofgraphtheory, suchastrafficnetworks,navigablenetworksandoptimalroutingforemergencyresponse,placementofelectricvehiclechargingstationsandgraphtheoreticmethodsinmolecularepidemiology.Becauseoftherapidgrowthof researchinthisfield,thefocusofthebookisontheup-to-datedevelopment oftheaforementionedapplications.
Theproposedbookwillbeidealforresearchers,engineers,transportplannersandemergencyresponsespecialistswhoareinterestedintherecent developmentofgraphtheoryapplications.Moreover,thisbookcanbeusedas teachingmaterialforpostgraduatestudentsbecause,inadditiontoup-to-date descriptionsoftheapplications,itincludesexercisesandtheirsolutions.Some oftheexercisesmimicpractical,real-lifesituations.Advancedstudentsin graphtheory,computerscienceorbiologymayusetheproblemsandresearch methodspresentedinthisbooktodeveloptheirfinal-yearprojects,master’s thesesordoctoraldissertations;however,tousetheinformationeffectively, specialknowledgeofgraphtheorywouldberequired.
Thechaptersofthisbookareindependentandcanbereadinanyorder, givingthereaderfreedomandcontrolovertheirreadingexperience.Another featureistheinclusionofanintroductorychapter,whichprovidesanoverview ofmanyimportantapplicationsofgraphtheoryandbasicgraph-theoretic algorithms.Itistheauthor’shopethatthispublicationoftherecentdevelopmentofgraphtheoryapplicationswillinstigatefurtherresearchinthefield.
TheAuthor
DrVadimZverovich(MSc,1989;PhD,1993;Docent,2000)istheHeadofthe MathematicsandStatisticsResearchGroupattheUniversityoftheWestof England(UWE)inBristol.Anaccomplishedresearcher,heisalsoaFellow oftheUnitedKingdomOperationalResearchSociety,andwaspreviouslya FellowoftheprestigiousAlexandervonHumboldtFoundationinGermany.In 2016,DrZverovichwasawardedHigherEducationAcademyfellowshipstatus, andtheFacultyofEnvironmentandTechnologyoftheUWEnamedhimits researcheroftheyearin2017.DrZverovich’sresearchinterestsincludegraph theoryanditsapplications,networks,probabilisticmethods,combinatorial
optimizationandemergencyresponses.With30yearsofresearchexperience, hehaspublishedmanyresearcharticlesandtwobooksontheabovesubjects andestablishedaninternationallyrecognizedacademictrackrecordinthe mathematicalsciencescoveringboththeoreticalandappliedaspects.
Email:vadim.zverovich@uwe.ac.uk
Disclaimer
Anystatementsinthisbookmightbefictitiousandtheyrepresenttheauthor’s opinion.
Introduction
Inthischapter,wewillgiveabriefoverviewofselectedapplicationsofgraph theory,manyofwhichgaverisetothedevelopmentofgraphtheoryitself.A rangeofsuchapplicationsextendsfrompuzzlesandgamestoveryserious scientificandreal-lifeproblems,thusillustratingthediversityofapplications. Thefirstsectionisdevotedtothesixearliestapplicationsofgraphtheory. Thenextsectionintroducesso-calledscale-freenetworks,whichincludethe webgraph,socialandbiologicalnetworks.Thelastsectiondescribessomeof thebasicgraph-theoreticalgorithmswhichcanbeusedtotackleanumberof interestingapplicationsandproblemsofgraphtheory.
1.1EarlyApplicationsofGraphTheory
Inthissection,wewillbrieflydiscussearlyapplicationsofgraphtheory,which arewelldescribedintheexistingliterature.A graph G isanorderedpair (V,E),where V isanon-emptyandfinitesetof vertices,and E isasetof someunorderedpairsof V ,whicharecalled edges.Thevertexsetandtheedge setofagraph G mayalsobedenotedby V(G) and E(G) toavoidconfusion. Whendealingwithapplicationsofgraphtheory,theterms‘graphs’,‘vertices’ and‘edges’canbecalled‘networks’,‘nodes’and‘links’,respectively.Insome cases,directededgescanbeconsidered—thiswillalwaysbeobviousfromthe context.
1.1.1TheKönigsbergBridgeProblemandEulerianGraphs
In1736,EulersolvedthefamousKönigsbergBridgeProblem[17],whichwas theveryfirstproblemformulatedandsolvedintermsofgraphtheory.The problemwastofindaroundtourinKönigsbergwhereeachoftheseven bridgeswasvisitedexactlyonce(seeFigure1.1).Theinitialimportantstep, whichislefttothereaderasanexerciseattheendofthischapter,istorepresent thecitywithsevenbridgesasagraph.Intermsofgraphtheory,aroundtour
Fig.1.1 SevenbridgesofKönigsberg. (CopperengravingbyM.Merian,Photo: akg-images)
inagraphisacycle;thatis,aclosedwalkwhereverticesmayberepeated. Nowadays,ifagraphhasacyclethatvisitseachedgeexactlyonce,thensucha cycleiscalled eulerian andthegraphitselfiscalledan euleriangraph.Hereis theveryfirstresultingraphtheory,whichisattributabletoEuler:
Theorem1.1 [17] Aconnectedgraph G iseulerianifandonlyifeveryvertex of G hasevendegree.
Thewell-knownFleuryalgorithm[18]andHierholzeralgorithm[26]find aneuleriancycleinaneuleriangraph,butthelatterismoreefficient.Notethat euleriancyclescanbeusedinDNAfragmentassemblyandotherpractical applicationssuchasmailcarriersroutingandfloordesigns.
1.1.2Kirchhoff’sLawsforElectricalNetworks
Morethan100yearsafterEuler’sarticle,in1847,Kirchhoff[28]modelled electricalnetworksbytheirunderlyinggraphs.Interestingly,Kirchhoffwas borninKönigsberg,wherehegraduatedfromalocaluniversity.Kirchhoff developedthetheoryoftrees,whichareasubclassofallgraphs,todescribe
Fig.1.2 Kirchhoff’slaws.
thecurrentaroundeverycycleinanelectricalnetwork.Moreprecisely,his constructionwasbasedontheindependentcyclesofagraph,whichcan befoundbymeansofaspanningtree.Kirchhoff’sfirstlawisdevotedto conservationofcurrent:
Kirchhoff’sFirstLaw [28] Atanynode v inanelectricalnetwork,thesumof thecurrentsentering v isequaltothesumofthecurrentsleavingthenode v
Kirchhoff’ssecondlawdealswithconservationofenergy:
Kirchhoff’sSecondLaw [28] Thealgebraicsumofallvoltagesaroundany cycleinanelectricalnetworkisequaltozero.
Kirchhoff’sfirstandsecondlawsarealsocalledKirchhoff’sCurrentLawand VoltageLaw,respectively.TheselawsareillustratedinFigure1.2.
1.1.3TheFour-ColourProblem
TheFour-ColourProblemhasdefinitelybeenthemostfamousproblemin graphtheory:isittruethatanymaponaplanecanbecolouredwithatmost fourcoloursinsuchawaythatadjacentcountrieshavedifferentcolours? ThisproblemwasdiscussedbyGuthrieandDeMorganinca.1850,anditis possiblethatMöbiusknewtheproblemevenearlier.TheFour-ColourProblem caneasilybereformulatedintermsofgraphtheoryifcountriesarereplaced byvertices,andtwoverticesareadjacent(i.e.connectedbyanedge)ifthe correspondingcountriesshareaboundary.Thus,theproblemistocolourthe verticesofaplanargraphwithatmostfourcoloursinsuchawaythatadjacent verticeshavedifferentcolours.Thereisalonghistoryofattemptstoprovethat
Fig.1.3 ExtractfromDeMorgan’slettertoHamiltonabouttheFour-Colour Problem(1852,Dublin).
fourcoloursareenoughorfindacounterexample.Finally,in1977,Appeland Hakengavealong‘algorithmic’proofwiththeaidofacomputerprogram, butareasonablyshortandelegantproofoftheFour-ColourTheoremisyetto befound.
Four-ColourTheorem [3,4,5] Everyplanargraphisfour-colourable.
Therearemanyinterestingapplicationsofgraphcolouring:mobileradio frequencyassignment,scheduling/timetabling,registerallocationincompiler optimizationetc.
1.1.4Hamilton’sGamesandHamiltonianGraphs
SirWilliamRowanHamilton[22,23]inca.1857inventedtheIcosianGame, whichincluded15examplepuzzlesandwasbasedonatwo-dimensional(2D) representationofadodecahedronwith20vertices(seeFigure1.4a).
AnotherversionofthegamewithsimplifiedruleswascalledtheTraveller’s Dodecahedron.Inthisgame,thedodecahedronhastheformofasemi-sphere withahandle,whichlookslikeawoodenmushroom,andits20vertices representcities(seeFigure1.4c).Theideaofthepuzzlewastotravelaroundthe world(i.e.thesemi-sphere)andattempttofindaroundtourwhichwouldvisit eachcityexactlyonce.Intermsofgraphtheory,sucharoundtourinagraph isaspanningsimplecycle.Inotherwords,allverticesareincludedinthecycle andtheyarenotrepeated,apartfromthefirstandthelast.Suchacycleiscalled hamiltonian,andagraphiscalled hamiltonian ifithasahamiltoniancycle.
Fig.1.4 a)TheIcosianGame;b)ceramicpegs;c)theTraveller’sDodecahedron. (©2018ThePuzzleMuseum/JCD.http://puzzlemuseum.org)
Therearemanyresultsdevotedtohamiltoniangraphs,butacomplete characterizationofsuchgraphsisunknown.Thefollowingsufficientcondition foragraphtobehamiltonianisduetoDirac:
Theorem1.2 [14] Let G beagraphwith n vertices, n ≥ 3.Ifeveryvertexof G hasdegreeatleast n/2,then G ishamiltonian.
Hamiltoniancyclesarecloselyrelatedtothetravellingsalesmanproblem (TSP),whichhasnumerousimportantapplications.Infact,givenaweighted graph,theTSPseekstofindahamiltoniancycleofthesmallestpossibleweight. Theweightofanedgemightbedefinedasthedistancebetweenitsendvertices,thecostoftravelbetweenthemetc.ApplicationsoftheTSPinclude jobscheduling,vehicleroutingandcomputerwiring,tonameafew.
1.1.5ChemicalIsomersandEnumerationofTrees
In1857,Cayley[10]studiedanapplicationofgraphsinorganicchemistry, whichisbasedontrees.Theproblemwastocountthenumberofisomers ofthe saturatedhydrocarbons CnH2n+2,alsocalled paraffins,where n isthe numberofcarbonatoms.Forexample,C1H4 representsmethane,andC3H8 standsforpropane.ButaneandisobutanehavethesameformulaC4H10,see Figure1.5.Thus,theproblemwastoenumeratetreesinwhicheveryvertex hasdegree1or4.Thestartingpointwastosimplifytheproblemandcount labelledtrees:
Theorem1.3 [9] Thereare nn 2 labelledtreeswith n vertices.
Fig.1.5 Butaneandisobutane(C4H10).
Thisformulaalsogivesthenumberofspanningtreesinacompletelabelled graph.Thefollowingtheoremprovidesthenumberoflabelledtreeswitha givendegreesequence:
Theorem1.4 [33,34,40] Thenumberoflabelledtreeswithadegreesequence (d1,d2,...,dn) isequaltothemultinomialcoefficient
Itmaybepointedoutthatcountingunlabelledtrees(uptoisomorphism)is amorechallengingproblem—noexactformulaisknownyet.
1.1.6ChessboardPuzzles
Weconcludethissectionwiththefamouseightqueenspuzzle,whichwas publishedin1848bytheGermanchessplayerBezzel[7].Theproblemis toplaceeightqueensonastandard 8 × 8 chessboardinsuchawaythatno twoqueensattackeachother.Thismeansthatanytwoqueenscannotbein thesamecolumn,rowordiagonal.Itisnottoodifficulttofindaparticular solutiontothispuzzle,sotheproblemwaslaterextendedtofindingall possiblesolutions.Twoyearslater,in1850,Nauckindependentlyproposed theextendedversionofthepuzzle[35]andalsopublishedall92solutions[36]. Noticethatactuallythereare12basicsolutionsifsymmetry(reflectionand rotation)istakenintoaccount.Interestingly,Gausshadalsobeeninvolvedin solvingthepuzzle,see[38]forfurtherdetails.
Althoughtheeightqueenspuzzleisnotformulatedintermsofgraph theory,thechessboardcanberepresentedbythe queengraph,wherevertices aresquaresofthechessboardandtwodifferentverticesareadjacentifthe correspondingsquaresareinthesamecolumn,rowordiagonal.Thus,itis necessarytofindallindependentsetsofsize8inthequeengraph.In1972, Dijkstra[11]developedadepth-firstbacktrackingalgorithmtosolvethis problem.Similarquestionscanbeposedforotherchesspieces:king,rook, bishopandknight;andtheycanbeextendedtoan n × n chessboard.
In1862,deJaenisch[12]consideredtheproblemoffindingthesmallest dominatingsetinthequeengraph;thatis,thesmallestcollectionofqueens whichwouldthreatenallunoccupiedsquares.Similartotheeightqueens puzzle,thedominationproblemwasgeneralizedforan n × n chessboard.
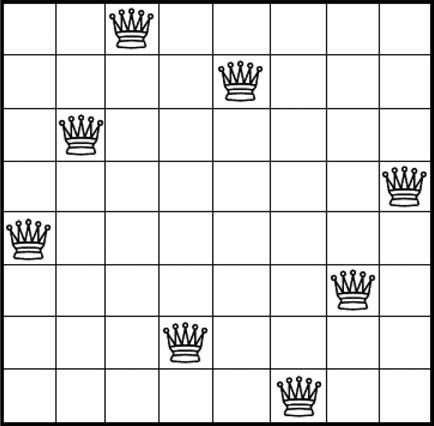
Fig.1.6 Oneoftwelvesolutionsoftheeightqueenspuzzle.
1.2Scale-FreeNetworks
Inthissection,wewilldiscusssomenetworkswhosedegreedistributions followapowerlaw.Suchnetworksarecalled scale-freenetworks,andthey aretypicallyverylarge,sparsegraphswithasmallworldstructure.These propertiesareexplainedbelow.
Inagivengraph G with n vertices,let nk denotethe numberofverticesof degree k,andletthesequence
(nk, 0 ≤ k ≤ n 1)
bethe degreedistribution of G.Thedegreedistributionof G issaidtofollowa powerlaw if,foreverydegree k> 0, nk n ∼ 1 kγ , (1.1) where γ> 1 isafixedconstant.Thenumber P(k)= nk n
scale-freenetworks9 istheproportionofverticesofdegree k anditcanbeviewedasaprobability thatavertexisofdegree k.Theasymptoticrelationship(1.1)isapplicable forinfinitegraphs,andforfinitegraphsitmeans‘approximatelyequalto’: P(k) ≈ k γ .Inthecasewhen G isadirectedgraph,thepowerlawsfortheindegreedistributionandtheout-degreedistributionaredefinedanalogously.
Anunusualfeatureofthepowerlawdistributionisitsbroadtailrepresentingapolynomialdecaywhen k tendstoinfinity,asopposedtotypical distributionswithexponentialdecay.Thismeansthatinmassivepower-law graphsthereareverticesofhighdegree,whicharecalled hubs.Itmayalsobe mentionedthatinrealnetworksthepowerlawmayhavesomediscrepancies forverticesofverysmallandlargedegrees.
Althoughthepowerlawdistributionistypicallyapplicabletomassive graphs,letusconsiderasmallgraph G with17vertices.If G hasdegree sequence (1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 3
, thenitsdegreedistributionis (0, 10, 4,
0) Wecanseethat,apartfrom somediscrepancyforverticesofdegree1,thegraph G approximatelyfollows apowerlawwithexponent γ =2:
1.2.1TheWebGraphandSimilarTechnologicalNetworks
Thewebgraphisarelativelynewphenomenon,whichappearedafterthebirth oftheinternetintheearly1980s.Noticethattheinternetisamoregeneral term,whichincludese-mail,hardwareandothercomponents.Inthe web graph W,verticesrepresentwebpagesandedgesarethehyperlinksbetween webpages.Althoughthehyperlinksaredirectededges,insomecases W canbe viewedasanundirectedgraph.Thewebgraph W isareal-worldgraph,which iscontinuouslydevelopingovertime.Also,therearedynamicwebpages(e.g. anonlineclock)andthenumberofsuchpagescanbeviewedasinfinite.Hence, thewebgraph W maybeconsideredaseitherfiniteorinfinite.
Letusbrieflydiscusssomeimportantpropertiesof W.Firstly,itisan immensegraphwithbillionsofvertices.Secondly, W isarelativelysparse graphbecausethenumberofedgesin W ismuchlessthanthenumberof allpossibleedges.Moreprecisely,theaveragedegreeofafixedvertexin W doesnotexceedaconstant[6].Thirdly,thewebgraphhasmany‘communities’. A community isasetofwebpageshavingacommoninterest.Thereare
severalapproachesfordefiningcommunitiesmathematically.Onemaydefine acommunityasasubgraphhavingmoreinternaledgesthanexternal.Another definitionisbasedondensedirectedbipartitesubgraphs,whicharecalled bipartitecores.Anexampleofabipartitecoreisadirectedcompletebipartite graph K3,3,wherethedirectededgesgofromoneparttoanother,andsome directededgesmaybeaddedtotheparts.
Oneofthemostimportantpropertiesof W isthepowerlawdegree distribution.Itimpliesthatmostverticeshaveasmallnumberofincident edges,whereasafewvertices(hubnodes)havealargenumberofincident edges.Thereissomeevidenceintheexistingliterature[2,8]thattheindegreedistributionofthewebgraph W followsapowerlawwith γ =2.1, whereas γ =2.5 or2.7forthepowerlawout-degreedistribution.
Thewebgraph W possessestheso-calledsmall-worldpropertyintroduced in[41].Let d(u,v) denotethedistancebetweenvertices u and v inan undirectedgraph G,andlet X consistofallpairsofdifferentverticesforwhich d(u,v) isfinite.The averagedistance of G isdefinedasfollows: L(G)= ∑ u,v∈X d(u,v) | X | .
Foraconnectedgraph G withthevertexset V ,thisdefinitioncanberewritten inthefollowingway: L(G)= ( n 2 ) 1 ∑
(u,v).
∈V
Asimilarparameter, Ld(G),canbedefinedforadirectedgraph G,wherethe distancebetweentwoverticesisthenumberofedgesintheshortestdirected pathbetweenthosevertices.Thesmall-worldpropertysaysthat L(G) (or Ld(G))shouldbemuchsmallerthanthenumberofverticesin G:
L(G) ≤ c lnln n, where c issomesmallconstant.Forthewebgraph W,itwasreportedinthe literature[2,8]that L(W)=6.8,whereas Ld(W)=16 or19.
Anothercharacteristicofasmall-worldgraphreflectsitslocaldensity,which shouldberelativelylargecomparedwithstandardrandomgraphshavingthe samenumberofverticesandedges.If N (v)denotesthesetofverticesadjacent
toavertex v,then | E⟨N (v)⟩| isthenumberofedgesinthegraphinducedby N (v).Thisnumberisactuallythenumberoftriangles(i.e.cycles C3)passing through v.The clusteringcoefficientofavertex v isdefinedasfollows:
(v)= | E⟨N (v)⟩| ( deg(v) 2 )
If v hasdegree k andthereare q edgesintheneighbourhood N (v),then
(v)= 2q k(k 1)
Nowwecandefinethe clusteringcoefficientof G:
Basedonalargesampleofthewebgraph,itwasreportedin[1]that C(W)= 0.1078,whereas C(R)=0.0002forarandomgraph R withthesamenumber ofverticesandedges.Forthedirectedinterpretationofthewebgraphandthe clusteringcoefficient,itwasalsoreportedthat Cd(W)=0 081 and Cd(R)= 0 001.Thisconfirmstheclaimthattheclusteringcoefficientofthewebgraph ismuchlargercomparedwitharandomgraphhavingthesamenumberof verticesandedges.
Theinternethasdifferentstructurallevels,hencethe internetgraph I can bedefineddifferently.Forexample,verticesof I mayrepresentdomainsand edgesareconnectionsbetweendomains.Alternatively,verticesof I canbe routersandedgesareconnectionsbetweenrouters.Bothoftheseinternet graphsfollowapowerlawwithexponent γ =2.5.Thebloggraphisaninduced subgraphofthewebgraph,whereverticesrepresentwebblogsanddirected edgesarethelinksbetweenblogs.Thisgraphfollowsapowerlawwith exponent γ =2 1 forbothin-degreeandout-degreedistributions,andithas arichcommunitystructure.Inthe callgraph,verticesrepresenttelephone numbersandtwoverticesareconnectediftherewasatelephonecallfromone numbertotheotherover,say,oneday.Thedirectedcallgraphalsofollowsa powerlawwithexponent γ =2.1.
Furtherinterestingpropertiesoftheaforementionedgraphs,suchas betweennessandordersofconnectedcomponents,canbefoundintheexisting literature(e.g.see[15]).