MagneticSmall-AngleNeutron Scattering
OXFORDSERIESONNEUTRONSCATTERINGIN CONDENSEDMATTER
1.W.G.Williams: Polarizedneutrons
2.E.BalcarandS.W.Lovesey: Theoryofmagneticneutron andphotonscattering
3.V.F.Sears: Neutronoptics
4.M.F.Collins: Magneticcriticalscattering
5.V.K.Ignatovich: Thephysicsofultracoldneutrons
6.Yu.A.Alexandrov: Fundamentalpropertiesoftheneutron
7.P.A.Egelstaff: Anintroductiontotheliquidstate
8.J.S.HigginsandH.C.Benoˆ ıt: Polymersandneutronscattering
9.H.Glyde: Excitationsinliquidandsolidhelium
10.V.BalucaniandM.Zoppi: Dynamicsoftheliquidstate
11.T.J.Hicks: Magnetismindisorder
12.H.RauchandS.Werner: Neutroninterferometry
13.R.Hempelmann: Quasielasticneutronscatteringandsolidstatediffusion
14.V.M.NieldandD.A.Kean: Diffuseneutronscattering fromcrystallinematerials
15.E.H.KisiandC.J.Howard: Applicationsofneutronpowderdiffraction
MagneticSmall-AngleNeutronScattering
AProbeforMesoscaleMagnetismAnalysis
AndreasMichels UniversityofLuxembourg
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries
c AndreasMichels2021
Themoralrightsoftheauthorhavebeenasserted
FirstEditionpublishedin2021
Impression:1
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica
BritishLibraryCataloguinginPublicationData Dataavailable
LibraryofCongressControlNumber:2021932525
ISBN978–0–19–885517–0
DOI:10.1093/oso/9780198855170.001.0001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
Thisbookisdedicatedtothememoryofmyparents,andtoAnnaandNiki.
Preface
Oneoftheveryfirstpublicationsonmagneticsmall-angleneutronscattering(SANS) is“DepolarisationundKleinwinkelstreuungvonNeutronendurchGitterfehlerinferromagnetischenKristallen”byHelmutKronm¨uller,AlfredSeeger,andManfredWilkens from1963[1].ThepaperiswritteninGerman(Englishtranslation:“Depolarization andsmall-anglescatteringofneutronsbylatticeimperfectionsinferromagneticcrystals”)andwasdedicatedtoMaxBornontheoccasionofhis80thbirthday.Intheir theoreticalstudy,theauthorshavepioneeredtheuseofthecontinuumtheoryofmicromagneticsforcalculatingthemagneticSANScrosssectionofmagneticmaterials. Specifically,Kronm¨uller,Seeger,andWilkensstudiedthespindisorderthatisrelated tothestrainfieldsofdislocations:inmechanicallydeformedmetals,themagnetization ishighlyinhomogeneousinthevicinityofdislocations,whichisduetothepresenceof magnetoelasticcoupling.Theassociatedstaticlong-wavelengthmagnetizationfluctuationsrepresentacontrastforelasticmagneticSANS,andthescatteringcrosssection canbecomputedbymeansofmicromagnetictheoryforsamplesclosetomagnetic saturation.ThistypeofmagneticSANS,denotedasspin-misalignmentscattering, isrelatedtospatialvariationsintheorientationandmagnitudeofthemagnetization.Ithasbeenpredictedtobeabout10 100timeslargerthanthenuclearSANS thatisrelatedtothevolumedilatationsofdislocations.Withtheadventofnuclear researchreactorsandtheconcomitantconstructionanddevelopmentofthefirstdedicatedSANSinstruments,e.g.,atJ¨ulich[2]andGrenoble[3],startedtheexploration ofmagnetismandsuperconductivityonamesoscopiclengthscaleusingneutronsas aprobe.Themainideasof[1]werethenverifiedandextendedonlylaterinSANS experimentsoncold-workedsinglecrystals,assummarizedin[2,4–6].
Besidesbeingapioneeringstudythatisfullofinsightsregardingthecomplexityoftheinteractionbetweenlatticeimperfectionsandspinstructure,theworkby Kronm¨uller,Seeger,andWilkenshasundoubtlydemonstratedthefactthatmagnetic SANSisinmanyrespectsdifferentthanthe(nonmagnetic)small-anglescatteringby structuralandchemicalinhomogeneities.Thelatterstatementmaybeconsideredas theparadigmforthisbook.Itcertainlyservedasthecentralmotivationfortheauthortowriteit.NuclearSANSandsmall-anglex-rayscatteringarelargelybasedon theparticle-matrixconcept,withparticleformfactorsandstructurefactorsbeingthe basicquantities.MagneticSANSisaboutthemagnetizationdistribution.Theparticle formfactorisobtainedasthesolutionofavolumeintegral,whilethestructure-factor problem,relatedtothearrangementofandtheinteractionbetweentheparticles, maybesolvedbyusingthemethodsofstatisticalmechanics.Ontheotherhand, thecontinuousvectorialmagnetizationdistributionofamagneticmaterialisobtained bysolvingasetofnonlinearpartialdifferentialequations(knownasBrown’sequations[7]),whichinthecontextofmagneticSANS—anddespitetheearlywork[1]—is
viii Preface
anoftenoverlookedfact.Still,manymagneticSANSstudiesanalyzetheirdatabased ontheparticle-matrixconcept,withtheunderlyingshortcomingassumptionofhomogeneouslymagnetizeddomains,andneglecttheimportantandoftenevendominant magneticscatteringcontributionduetomisalignedmagneticmoments.
Asonemayanticipatefromthepreviousconsiderations,theoriginofmagnetic SANSisverycloselyrelatedtothepresenceoflatticedefectsinthemicrostructureof magneticmaterials(e.g.,vacancies,dislocations,grainboundaries,pores).ThisviewpointhasalsobeenemphasizedintheearlySANSreviewbySpringerandSchmatz[8]. OnthemesoscopiclengthscalethatisprobedbyconventionalSANS(∼1 300nm), thedefectsarelocallydecoratedbynanoscalespindisorder,whichisgeneratedby (i)spatialvariationsinthemagneticanisotropyfield,andby(ii)spatialvariationsin themagneticmaterialsparameters,mostnotablythelocalsaturationmagnetization. Tobemorespecific,forcesduetothedistortionofthecrystallatticeinthevicinityof amicrostructuraldefecttendtorotatethelocalmagnetizationvectorfieldalongthe mainaxesofthesystemofinternalstresses(magnetoelasticcoupling),whilemagnetocrystallineanisotropytriestopullthemagneticmomentsalongtheprincipalaxesof thecrystal[7].Likewise,nanoscalespatialvariationsofthesaturationmagnetization, exchange,oranisotropyconstants(e.g.,atinternalinterfacesinamagneticnanocompositeorinananoporousferromagnet)giverisetoinhomogeneousmagnetization states,whichrepresentacontrastformagneticSANS.Itisofdecisiveimportanceto emphasizethattheadjustmentofthemagnetizationalongtherespectivelocaleasy axesdoesnotoccurabruptly,i.e.,onascaleoftheinteratomicspacing,buttakes placeoveramoreextendedrange.Thisisaconsequenceofthequantum-mechanical exchangeinteraction,whichspreadslocalperturbationsinthemagnetizationover largerdistances.Thesizeofsuchspininhomogeneitiesischaracterizedbythemicromagneticexchangelength lH,whichvariescontinuouslywiththeappliedfieldand takesonvaluesbetweenabout1 100nm.Theensuingmagneticneutronscattering appearsatscatteringangles ψ ∼ = λ/lH (with λ theneutronwavelength),aregime whichisroutinelyaccessiblebytheSANStechnique.Wealsoemphasizethatthe observationthatlattice-defect-inducedmagnetizationnonuniformitiesarecontinuous functionsofthepositiondoesnotimplytheabsenceofsharpfeaturesinthenuclear grainmicrostructure;forinstance,theremaywellexistsharpparticle-matrixinterfaces (e.g.,inthechemicalcomposition)inamagneticmaterial,butthecorrespondingspin distribution(whichdecoratestheseinterfaces)iscontinuousoverthedefects.Thisis nothingmorethansayingthatthemagneticmicrostructureinrealspacecorresponds totheconvolutionofthenucleargrainmicrostructurewithmicromagneticresponse functionswhichvarywithpositionandfield.Therefore,particleformfactorsmayalso appearwithinthemicromagneticdescriptionofmagneticSANS,buttheynaturally emergeinthecourseofacalculation,byspecifyingthegeometryofthedefect.
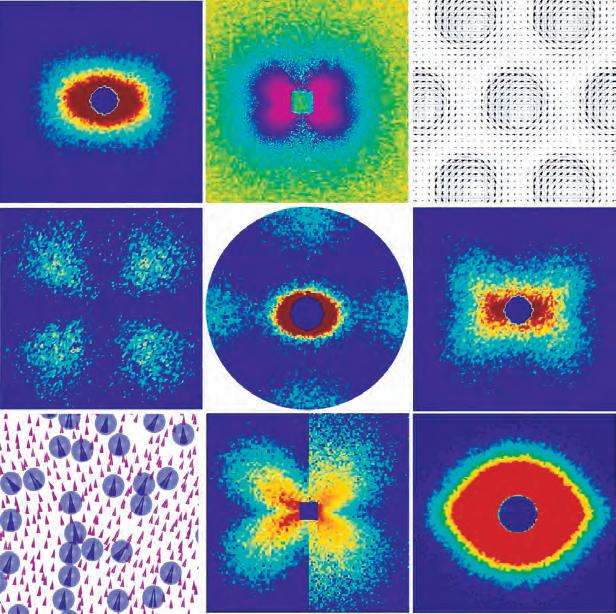
TherichnessandthecomplexcharacterofmagneticSANScanbegraspedby lookingatthefigureattheendofthispreface,whichdepictsaselectionofcomputed spinstructuresandexperimentalmagneticSANScrosssectionsofvariouspolycrystallinemagneticmaterials.Whiletheangularanisotropieswhicharevisibleinsomeof thecross-sectionimagesareexclusivelyrelatedtothesaturatedmagnetizationstate, otherpatternshavetheirorigininthenonuniformmagnetizationdistributionofthe
Preface ix
material,whichdependsonthemagneticinteractionsandonthecharacteristicsofthe underlyingmicrostructure.Thedisplayedanisotropiesobviouslygobeyondthewellknownsin2 α dependencyofmagneticneutronscattering,whichepitomizesthehomogeneouslymagnetizedsingle-domainstate.Theycanonlybeunderstoodbyanalyzing thespindistributionofthematerial,i.e.,bycarryingoutmicromagneticcalculationsof theSANScrosssection.Sincethestandardtextbooksonsmall-anglescattering[9–13] donotcoverthesubjectofmagneticSANSinsufficientdepth,webelievethatthere isthenecessitytofillthisgapwiththepresentbook.
Thecentralaimofthebookistoprovideanintroductionintothetheoretical backgroundthatisrequiredtocomputeSANScrosssectionsandcorrelationfunctions relatedtolong-wavelengthmagnetizationstructures;andtoscrutinizetheseconcepts basedonthediscussionofexperimentalunpolarizedandpolarizedneutrondata.The bookisprimarilyaboutthetechniqueofmagneticSANS,notaboutmaterials.Itswritingstyleanddictionmaybedescribedasamixturebetweenmonograph,textbook,and reviewarticle(inparticularChapter5).Regardingpriorbackgroundknowledge,some familiaritywiththebasicmagneticinteractionsandphenomenaaswellasscattering theoryisdesired.ThetargetaudienceconsistsofPh.D.studentsandpostdoctoraland seniorresearchersworkinginthefieldofmagnetismandmagneticmaterialswhowish tomakeefficientuseofthemagneticSANSmethod.Theprinciplesandmethodsthat arelaidoutinthisbookwillhopefullyenablethemtoanalyzeandinterprettheir SANSexperiments.
BesidesexposingthedifferentoriginsofmagneticSANS(Chapter1),andfurnishingthebasicsofthemagneticSANStechnique(Chapter2),alargepartofthebook isdevotedtoacomprehensivetreatmentofthecontinuumtheoryofmicromagnetics (Chapter3),asitisrelevantforthestudyoftheelasticmagneticSANScrosssection.AnalyticalexpressionsforthemagnetizationFouriercomponentsallowoneto highlighttheessentialfeaturesofmagneticSANSandtoanalyzeexperimentaldata bothinreciprocal(Chapter4)aswellasinrealspace(Chapter6).Chapter5provides anoverviewonthemagneticSANSofnanoparticlesandso-calledcomplexsystems (e.g.,ferrofluids,magneticsteels,spinglassesandamorphousmagnets).Itisthissubfieldwhereweexpectamajorprogresstobemadeinthecomingyears,mainlyvia theincreasedusageofnumericalmicromagneticsimulations(Chapter7),whichisa verypromisingapproachfortheunderstandingofthemagneticSANSfromsystems exhibitingnanoscalespininhomogeneity.
Beingtheresultofmorethantwodecadesofresearch,thebookcontainsthe contributionsofmanypeopleinoneorotherform.Iwouldliketoexpressmysincere gratitudetomyformerandpresentmasterandPh.D.students,postdocs,andtothe manycollaboratorsandcolleaguesworldwide.Veryspecialthanksaredueto:Michael Adams,NatalieBaddour,PhilippBender,FrankBergner,DmitryBerkov,Salvino Ciccariello,SergeyErokhin,ArtemFeoktystov,LuisFern´andezBarqu´ın,Arsen Goukassov,SergeyGrigoriev,PatrickHautle,DirkHonecker,JoachimKohlbrecher, ArtemMalyeyev,Jos´eLuisMart´ınez,KonstantinMetlov,DenisMettus,Sebastian M¨uhlbauer,YojiroOba,IvanTitov,andAndrewWildes.Theseresearcherstookover themostimportanttaskofcriticallyreadingvariouspartsofthebook,andtheir mostvaluablecommentsandsuggestionshavewithoutdoubtimprovedthefinal
x Preface
result.StephenLoveseyisthankedforhishelpinestablishingtheinitialcontact toOxfordUniversityPressandforhiscontinuousinterestintheprogressionofthe book.ItisalsoapleasuretoacknowledgethecontributionofRainerBirringer,who hasrelentlesslysupportedmethroughoutmyscientificcareer.Last,butnotleast,I wouldliketothankmyPh.D.adviser,J¨orgWeißm¨uller,whointroducedmetothe magneticSANStechnique.
Luxembourg AndreasMichels February2021
SelectionofcomputedspinstructuresandexperimentalmagneticSANScrosssections.
Acknowledgements
Iamindebtedtothefollowingcolleaguesforprovidingoriginaldataandfiguresoftheir ownresearch,whichhaveformedthebasisformanyillustrationsinthebook:Diego AlbaVenero,FrankBergner,DmitryBerkov,SabrinaDisch,SergeyErokhin,Patrick Hautle,Andr´eHeinemann,DirkHonecker,JoachimKohlbrecher,ChristianK¨ubel, DinaMergia,SebastianM¨uhlbauer,FeodorOgrin,RogerPynn,KiyonoriSuzuki, DmitriSvergun,LauraVivas,andAlbrechtWiedenmann.Iamalsogratefultothe followingpublishers,organizations,andlearnedsocietiesforpermissiontoreusemany figuresinthebook:EDPSciences,Elsevier,Springer,Taylor&Francis,Wiley,AmericanInstituteofPhysics,IEEEMagneticsSociety,InstituteofPhysicsPublishing, AmericanPhysicalSociety,DeutschePhysikalischeGesellschaft,andtheInternational UnionofCrystallography.TheUniversityofLuxembourg,theNationalResearchFund ofLuxembourg,andtheDeutscheForschungsgemeinschaftareacknowledgedforprovidingthefinancialmeanstocarryoutlargepartsofthisresearch.
INTRODUCTION
1.1Outlineofthebook
Small-angleneutronscattering(SANS)isapowerfulanduniquetechnique,whichallowsonetoinvestigatemicrostructural(densityandcompositionalfluctuations)aswell asmagneticinhomogeneitiesinthevolumeofmaterialsandonamesoscopiclength scalebetweenafewandafewhundrednanometers.AfurtheradvantageofSANS, comparede.g.,toelectron-microscopy-basedimagingmethods,isthatitprovidesstatisticallyaveragedinformationaboutalargenumberofscatteringobjects.Figure1.1 givesanoverviewonthemicrostructuralsizeregimeswhichareaccessiblebyvarious observationalmethods.WhenconventionalSANSissupplementedbyultraorvery small-angleneutronscattering(USANSorVSANS)thespatialresolutioncanbeextendeduptothemicrometerrange[14,15].Thisisanimportantsizeregimeinwhich manymacroscopicmaterialpropertiesarerealized.SinceSANSanditsx-raycounterpart,small-anglex-rayscattering(SAXS),areutilizedindiversefieldsofsciencesuch asmaterialsscience,physics,chemistry,biology,andinthederivedinterdisciplinary researchareas,thereexistsanenormousbodyofresearchliterature.Thestandardreferencesfornuclear(i.e.,nonmagnetic)SANSandSAXSarethewell-knowntextbooks byGuinierandFournet[9],GlatterandKratky[10],FeiginandSvergun[11],Svergun, Koch,Timmins,andMay[12],andbyGille[13].Foraselectionofreviewsonvariousmaterialsclassesandaspectsofsmall-anglescattering,forinstance,onbiological structures,polymers,ferrofluids,magneticmaterials,superconductors,disorderedand porousmaterialssuchascoal,fractalsystems,colloidalsuspensions,ceramics,steels, precipitatesinmetallicalloysandcomposites,defectclusters,ordislocationswerefer thereaderto[2,5,16–68].TheproceedingsoftheInternationalSmallAngleScattering Conference,whichareusuallypublishedinthe JournalofAppliedCrystallography,are alsoanexcellentsourceforfollowingthelatesttrendsanddevelopmentsinthefield. Fromthehistoricalpointofview,experimentalandtheoreticalprogressinthedomainofsmall-anglescatteringiscloselyconnectedtothedevelopmentoflaboratory SAXSmethods[9].Perhapsrelatedtothishistoricalperspectiveisthefactthatthe theoreticalconceptsandfoundationsofnuclearSANSandSAXSarerelativelywell developed—incontrasttomagneticSANS—andwidelyacknowledgedandappliedin experimentalstudies[9–13].Thisbookisdevotedto“diffuse”magneticSANS,i.e., magneticneutronscatteringatsmallscatteringanglesaroundtheforwarddirection arisingfromquasi-non-periodic,continuouslong-wavelengthmagnetizationfluctuations[comparepanel(A1)inFig.1.2].ThetermdiffusemagneticSANSisusedhere todistinguishitfrommagneticsmall-anglediffraction,whichisthemethodofchoice forinvestigatinglong-range-orderedperiodicstructuressuchashelicalspinsystems,
Fig.1.1:Microstructuralsizeregimesaccessiblebydifferentobservationalmethods. Thetechniquesrangefromneutrondiffraction,whichisusedtoinvestigateatomic structures,toopticalmicroscopy,whichcanbeemployedtoimagemacroscopicobjects suchasbacteriaorcrystallinegrainstructures.ImagecourtesyofRogerPynn,Indiana University,Bloomington,USA.After[69].
spin-densitywaves,flux-linelatticesinsuperconductors,ortherecentlydiscovered skyrmioncrystals[comparepanel(A2)inFig.1.2].Manyofthelatterproblemscan bedealtwithbymakinguseofthewell-knowncross-sectionexpressionsderivedinthe contextofmagneticsingle-crystalneutrondiffraction;forinstance,SANSstudiesof
Fig.1.2:Schematicillustrationofthetransformationfromrealspacetoreciprocal spaceforasmoothtexture(A1),adiscretelatticewithlatticespacing a (A2),anda smoothincommensuratemodulationontopofadiscretelattice(A3).After[64].
thevortexlatticecanbeconsideredascrystallographyofatwo-dimensionalsystemof lines(vortices),providinginformationaboutthelatticestructureandcorrelations,as wellastheinternalstructureoftheindividualscatterers[64].Therefore,thesetopics willnotbecoveredinthisbook,andlikewisesubjectssuchasneutroninstrumentation, datatreatment,ormultiplescattering.
Thebookisorganizedasfollows.InChapter1weintroducethebasicexpressions fortheneutronscatteringcrosssectionsand,inparticular,fortheelasticmagnetic differentialSANScrosssection.SpecialemphasisisputonthediscussionoftheoriginsofmagneticSANSandonitsdistinctnessfromconventionalparticlescattering. Chapter2isconcernedwithgeneralaspectsofSANSsuchastheexperimentalsetup, instrumentalresolution,theinfluenceofinelasticcontributionsduetophononand magnonscatteringtotheelasticSANScrosssection,thebasicsofnuclearSANS,the magneticSANScrosssectionsforthetwomostoftenusedscatteringgeometries,and theirrelationtotheparticle-matrixmodel.Chapter3introducesthecontinuumexpressionsforthemagneticenergycontributions,whichareemployedfordescribing themesoscalemagneticmicrostructureofmagneticmaterials.Itisthenshownhow thestaticequationsofmicromagnetics,theso-calledBrown’sequations,canbesolved inthehigh-fieldregimeandhowtheFouriercomponentsofthemagnetizationare relatedtothemagneticSANScrosssection.InChapter4weusetheresultsforthe Fouriercomponentstocomputetheunpolarizedandspin-polarizedSANScrosssections.TheseexpressionsservetohighlightcertainfeaturesofmagneticSANSsuch astheroleofthemagnetodipolarandDzyaloshinskii–Moriyainteraction,andare thenappliedtoanalyzeexperimentalSANSdataonvariousbulkmagneticmaterialssuchassoftandhardmagneticnanocomposites.Furthermore,Chapter4contains discussionsonthemagneticGuinierlawandontheasymptoticpower-lawexponents foundinmagneticSANSexperiments,aswellastwosectionssummarizingmagnetic SANSresultsonnanocrystallinerare-earthmetalsintheparamagnetictemperature
regimeandondislocations.Chapter5providesanoverviewonthemagneticSANS ofnanoparticlesandcomplexsystems,whichincludeferrofluids,magneticsteels,and spinglassesandamorphousmagnets.Wediscusstheunderlyingassumptionsofthe conventionalparticle-matrix-basedmodelofmagneticSANS,whichassumesuniformly magnetizeddomains,characteristice.g.,forsuperparamagnets,andweprovideacompletespecificationofthemicromagneticboundary-valueproblem.Firstattemptsto provideanalyticalexpressionsforthevortex-state-relatedmagneticSANSofthincirculardiscsareconsidered.Spin-misalignmentcorrelationsinrealspacearethesubject ofChapter6.Thecorrelationfunctionandcorrelationlengthofthespin-misalignment SANScrosssectionareintroduced,theirpropertiesarediscussedwithinthecontext ofmicromagnetictheory,andselectedexperimentaldataonNd–Fe–B-basedpermanentmagnetsandnanocrystallineelementalsoft(CoandNi)andhard(GdandTb) magnetsarereviewed.Finally,inChapter7wereportontheprogressmadeinusingfull-scalemicromagneticsimulationsfortheunderstandingofthefundamentalsof magneticSANS.ThesestudiestakeintoaccountthenonlinearityofBrown’sstatic equationsofmicromagnetics.Wediscussprototypicalsamplemicrostructures,theimplementationofthedifferentenergycontributions,andthestate-of-the-artregarding simulationsonmultiphasenanocompositesandnanoparticleassemblies.
1.2Basicpropertiesoftheneutronandnumericalrelations
Theneutronisanelementaryparticle,whichwasdiscoveredbyJamesChadwickin 1932[70].Thebasicpropertiesoftheneutronareitsmassof mn =1 675×10 27 kg,its zeronetelectricalcharge,anditsspinangularmomentumof S = ± 1 2 andassociated magneticdipolemomentof µn = 1 913µN ( isthePlanckconstant h dividedby2π and µN isthenuclearmagneton).Theseproperties,togetherwiththefactthatthe averagelifetimeofafreeneutronis ∼886s[71],renderneutronsextremelyattractive forresearchpurposes;inparticular,forinvestigatingthestructureanddynamicsof matteronawiderangeoflengthandtimescales;morespecifically:
• ThevalueoftheneutronmassresultsinadeBrogliewavelengthofresearchneutronswhichisoftheorderofinteratomicdistancesinmanycrystallineandliquid materials.Thisallowsonetoaccessthestructureofmatter.Likewise,sincethe typicalenergyofcoldandthermalneutronsisoftheorderoftheelementaryexcitationsinsolids,dynamicfeaturescanalsobeexploredbystudyingtheinelastic scatteringofneutrons.
• Thezeronetelectricalchargeimpliesthatneutronsinteractonlyveryweaklywith matter,incontrasttoe.g.,electrons,whicharesubjecttoaCoulombbarrier.As aconsequence,neutronsareabletopenetratedeeplyintomaterialsandthey interactwiththeatomicnucleiofthematerial.Fromatheoreticalpointofview, thisentailsthattheneutron-nucleusscatteringprocesscanbeanalyzedwithin first-orderperturbationtheory,whichinthecontextofscatteringformalismis knownastheBornapproximation[72].Multiple-scatteringeffectscanusuallybe ignored.Thiscircumstancefacilitatestheanalysisofneutronscatteringdata,since well-knownexpressionsforthenuclear(andmagnetic)scatteringcrosssections havebeenderivedforthiscase.
• Thescatteringlengthfortheneutron-nucleusinteractionvariesinanonsystematicmannerfromoneelementtotheotheracrosstheperiodictableof elements,andevenbetweentheisotopesofthesameelement(seeFig.2.11).This bringswithitanimportantadvantageofneutronscatteringoverx-rayscattering:lightelementssuchashydrogenoroxygenstronglyscatterneutrons,whereas theyonlyweaklyscatterx-rays,whichisaconsequenceofthefactthatthexrayscatteringlengthisproportionaltotheatomicnumber.Thenon-systematic variationofthenuclearscatteringlengthbetweenisotopesofthesameelement createsthepossibilitytotunetheneutronscatteringcrosssectionbyvaryingthe isotopicconcentration;forinstance,lightwater,H2O,hasatheoreticalmacroscopiccoherentscatteringcrosssectionpermoleculeofΣcoh =3 92 × 10 3 cm 1 , whereasforheavywater,D2O,onefindsΣcoh =0.512cm 1 (see,e.g.,chapter9 in[73]).Therelatedso-calledcontrast-variationtechniqueisofgreatimportance insoftmatterscience,wherecompoundscontainingmanyhydrogenmoleculesare usuallystudied.
• Themagneticmomentoftheneutroninteractswithunpairedelectronsofatoms. Hence,magneticstructureanddynamicscanbeinvestigatedbymeansofthis interaction.Magneticneutronscatteringmaybeasstrongasnuclearscattering. Infact,wewillseeinthisbookthatmagneticSANSduetolong-wavelength spin-misalignmentfluctuationscanbeseveralordersofmagnitudelargerthan thenuclearSANS.
Highlyenergeticneutronsareproducedbyeithernuclearfissionofheavynucleior byspallationofheavymetaltargets[74].Bymeansofamoderator(e.g.,lightwater, heavywater,graphite),theneutronsaresloweddowntotheenergyofthemoderator, wheretheneutron-velocityspectrumistoaverygoodapproximationdescribedbya Maxwelliandistribution[75].Thefollowingequationssummarizethebasicrelations forthedeBrogliewavelength λ,wavevector k0,momentum pn,andkineticenergy E0 ofaneutronmovingwithvelocity vn:
Bycomparingthekineticenergy E0 ofthemoderatedneutronstothethermalenergy kT ,neutronsforresearchpurposesarecommonlyclassifiedashot,thermal,andcold neutrons(seeTable1.1).Usingthevaluesforthephysicalconstants mn,h,and k (see
Table1.1 Classificationschemeforrangesofenergy,temperature,wavelength,andvelocity ofresearchneutrons.Theindicatedvaluescorrespondtothecold,thermal,andhotspectrum oftheILL(takenfrom[77]).
AppendixG),eqns(1.1) (1.4)suggestthefollowingnumericalrelationsbetweenthe involvedquantities[76]:
where λ isexpressedinunitsof ˚ A,
E0 inmeV,and T is indegreesofKelvin.
1.3Definitionsofscatteringcrosssections
TheneutronscatteringcrosssectionsaredefinedwithreferencetoFig.1.3,which depictsasketchofthegeneralscatteringgeometry.Inthefollowingconsiderationsthe spindegreeoffreedomoftheneutronisignored.Theincomingneutronsarecharacterizedbythewavevector k0 andtheenergy E0.Thesample(inacrystalline,amorphous, liquid,orgaseousstate)iscomposedof N scatteringatomsinthesamplevolume V .It ispositionedsuchthattheoriginofthecoordinatesystemisatsomearbitrarypoint withinthesample,e.g.,atthecenterofmassofthesystem.Theneutronsarescattered intoadirectionwhichisspecifiedbytheangles ψ and θ.Moreover,onecommonlyassumesthatthecharacteristicsizeofthesampleismuchsmallerthanthedistance betweenitandthedetector.Afterinteractionwiththesample,thewavevectorand energyoftheneutronsare,respectively,givenby k1 and E1 = 2k2 1 /(2mn).Thechange inthewavevectoroftheneutronsdefinesthemomentum-transferorscatteringvector
(1.7) whereastheneutron-energychangeisgivenby
Themomentumwhichistransferredtothetargetinthescatteringeventequals q. WithreferencetoFig.1.3oneeasilyfindsthat[74]
Fig.1.3:Sketchofthegeneralneutronscatteringgeometry.
Forelasticscattering(k0 = k1 = 2π λ and∆E =0),thecasewhichismostrelevantin thisbook,itisreadilyverifiedthatthemagnitudeof q isgivenby:
wherethelastapproximationbecomesvalidinthesmall-angleregime(ψ 1).The relation q ∼ = k0ψ forsmall-anglescatteringcanbeconnectedtoawell-knownresult fromclassicaloptics[78]:anobjectwithalineardimensionof Z givesrisetoaFraunhoferdiffractionpeakalongtheforwarddirectionwithanangularwidthof ψ ∼ = λ/Z; inotherwords,mostofthediffractedintensityisconcentratedatscatteringangles ψ λ/Z,whichtranslatesinto q 2π/Z.Fortypicalvaluesof λ =0.6nmand Z =10nm,wefind ψ ∼ = 3.4◦ . Thepartialordoubledifferentialneutronscatteringcrosssection d2 σ dΩdE1 isdefined as:
where n1 denotesthenumberofneutronswhicharescatteredpersecondintothe elementofsolidangle dΩ=sin ψdθdψ andwhichhaveafinalenergybetween E1 and E1 + dE1,andΦdenotestheincidentbeamflux,i.e.,thenumberofneutronsper secondthroughaunitarea,wheretheareaisassumedtobeperpendiculartothe directionoftheincidentneutronbeam.Thedimensionsof n1 andΦare,respectively, time 1 andtime 1 area 1,sothat d2 σ dΩdE1 iscommonlyexpressedinunitsofbarneV 1 , where1barn=10 24 cm2 and1eV=1 602 × 10 19 J.Integrating d2 σ dΩdE1 overallfinal energies,oneobtainsthedifferentialscatteringcrosssection:
where n2 equalsthetotalnumberofneutronswhicharescatteredpersecondinto dΩ. Thetotalscatteringcrosssection
isobtainedfrom dσ/dΩbyintegrationoveralldirections,where n3 denotesthetotal numberofneutronsscatteredpersecondatallenergiesandinalldirections.Inmany experimentalsituations—however,generallynotinmagneticSANS—dσ/dΩdepends onlyontheangle ψ,sothat
Both dσ/dΩand σ aregivenintheunitofthebarn.Inadditiontoelasticandinelastic scattering,neutronsmayberemovedfromtheincidentbeambyabsorptionwithinthe nucleiofthematerialunderstudy.Thisprocessischaracterizedbyanabsorptioncross section σa,sothatthetotalcollisionorextinctioncrosssection(takingintoaccount scatteringandabsorption)isgivenby
Thequantity σtot isrelatedviatheopticaltheorem,alsoknownastheBohr–Peierls–Placzekrelation,totheimaginarypartofthenuclearscatteringamplitude fN(ψ)along theforwarddirection(ψ =0)[72,79,80]:
Theopticaltheoremembodiestheconservationofparticlenumber,i.e.,thenumber ofincomingneutronsequalsthenumberofoutgoingneutronsplusthosewhichare captured[75].∗
Thetotalcollisioncrosssectionalsodeterminestheneutrontransmission.Assumingperpendicularneutronincidenceonaplanarslab-shapedsample,thesample transmission T isrelatedtotheatomicnumberdensity ρa = N/V (number N of nucleiinthesamplevolume V ), σtot,andthesamplethickness t bythewell-known Lambert–Beerlaw[82]: T =exp( ρaσtott)=exp( µt) , (1.17)
where µ = ρaσtot denotestheattenuationcoefficient(incm 1).Themeanfreepath oftheneutronbetweencollisionsisgivenby Lmfp = µ 1.For Lmfp t onehas
∗InthiscontextwerefertoTopervergetal.[81]foraninterestingpolarizedSANSstudyona ferrofluid,whichutilizestheopticaltheoremforanalyzingthewholerangeofthescatteringpattern includingthezoneoftheinterferencebetweenscatteredandtransmittedneutronwaves.
ElasticdifferentialSANScrosssection 9
T ∼ = 1andthesampleistransparenttoneutronswithaparticularenergy,while T ∼ = 0 for Lmfp t andthemediumisopaque.Valuesfor Lmfp dependontheneutron wavelengthand,fornot-too-stronglyabsorbingandscatteringmaterials,aretypically inthe0 1 10cmregime(seetable12.3in[83]).Asaruleofthumb,inordertoavoid multiplescatteringoneshouldaimfor T 90%[84,85](neglectingabsorption).
Finally,weremarkthatinthedomainofsmall-anglescatteringitiscustomaryto displaythemacroscopicdifferentialSANScrosssection dΣ/dΩperunitvolume(in cm 1),whichisrelatedtothemicroscopic dσ/dΩpernucleus[2]via
1.4ElasticdifferentialSANScrosssection
InaSANSexperiment,theenergyofthescatteredneutronsisusuallynotanalyzed andonemeasuresanenergy-integratedcrosssection,i.e.,thedetectorcountsneutrons thathavebeenscatteredelasticallyaswellasinelastically.However,itcanbeshown thatinelasticcoherentscatteringcontributions(e.g.,duetophononsand/ormagnons) playonlyaminorroleinthesmall-angleregime,sothatitisjustifiedinmanycases toconsiderSANSaselasticscattering(seeSection2.3).Theassumptionofelasticity impliesthattheinternalstatesofthesamplearenotchangedbythescatteringevent. FollowingLovesey[86]andSquires[76]andignoringthespinoftheneutron,theelastic differentialcrosssectioncanbecomputedbysummingupallscatteringprocessesin whichthestateoftheneutronchangesfrom k0 to k1,accordingto:
where Wk0→k1 denotesthenumberoftransitionspersecondfromthestate k0 tothe state k1.Thesumineqn(1.19)runsoverallvaluesofthefinalwavevector k1 thatlie withintheelementofsolidangle dΩ,keepingthevaluesof k0 constant.Thetransition ratecanbeevaluatedbyusingFermi’sgoldenrule[72,77]:
where ρk1 isthenumberoffinalmomentumstatesin dΩperunitenergyrange,and Vint denotestheinteractionpotentialbetweentheneutronandthescatterer(inducingthe transitionfrom k0 to k1).Byassumingthattheincomingandoutgoingneutronwaves areinaplane-wavestate,respectively, Ain ∝ exp(ik0 · r)and Aout ∝ exp(ik1 · r),the matrixelementeqn(1.20)canbeevaluated.Withinthisso-calledBornapproximation, andusingthedefinitionofthescatteringvector q [eqn(1.7)],thetransitionrate Wk0→k1 isthenproportionaltothemagnitudesquareoftheFouriertransformof theneutron-matterinteractionpotential.Thederivationoftheelasticnuclearand magneticneutronscatteringcrosssectionscanbefoundinmanytextbooksonneutron scattering(e.g.,[76,86])anditisthereforenotrepeatedindetailhere.Twointeractions aremostrelevantforthescatteringofthermalneutronsfrommatter,thenuclearand themagneticinteraction,whicharebrieflydiscussedinthefollowing.
1.4.1NuclearSANScrosssection
Theshort-rangeandisotropicneutron-nucleusinteractionismodeledbyFermi’s pseudopotential[87]:
where b istheatomicscatteringlengthofastronglyboundnucleussittingatthe origin r =0,and δ(r)isDirac’sdeltafunction.ItshouldbeemphasizedthatFermi’s pseudopotentialdoesnotreflecttheactualnuclearinteractionpotentialandthatthe assumptionsunderlyingtheBornapproximation,inparticular,theapproximationof theincomingneutronwavefunctionasaplanewavewithintheinteractionrangeofthe nuclearpotential(∼1fm;1fm=10 15 m),arenotvalidfortheverystrongnuclear potential(seethearticlebySchober[77]foradiscussionofthispoint).However, eqn(1.21)istheonlypotentialwhich,intheBornapproximation,yieldstherequired isotropic(s-wave)scatteringbehavior[76,86].
Thescatteringlengthisgenerallyacomplexquantitywhichcanbewrittenas[88]:
wheretherealpart b takesonpositiveaswellasnegativevaluesandisoftheorder ofafewfm(seeFig.2.11).Theimaginarypart b > 0describestheabsorptionof neutrons.Infact,itcanbeshownthatforallpracticalpurposestheabsorptioncross sectionisgivenby[82]
Notethat σa isinverselyproportionalto k0 and,hence,totheneutronvelocity vn. Equation(1.23)iscalledFermi’s1/vn-law.Nuclearscatteringlengthsareusuallytaken fromexperiment.Theycanbemeasuredwitharangeoftechniques;forinstanceby meansofmirrorreflection[89–93],withagravityrefractometer[94–97],orbyneutron interferometry[98–100](seethearticlebyRauchandWaschkowski[101]andthebook bySears[82]forfurtherdetails).Absorptionisnegligibleformostelementsandtheir isotopes(b |b |),however,thereexistafewisotopes(e.g., 3He, 10B, 113Cd, 157Gd) whichdopossessastrongneutroncapturecrosssection.Valuesfor b andforthe coherent σcoh,incoherent σinc,andabsorption σa crosssectionscanbefoundin[102]. Byinsertingtheinteractionpotentialeqn(1.21)intotheeqns(1.19)and(1.20)it canbeshownthattheelasticnucleardifferentialscatteringcrosssectionofacollection of N nucleiatpositions rk equals[76,103]:
wherethe bk denotethenuclearatomicscatteringlengths, i2 = 1,theasterisk(∗) marksthecomplex-conjugatedquantity,anditisunderstoodthat dΣnuc/dΩrepresentsanensemble-averagedquantity;morespecifically,anaverageovertheatomic
ElasticdifferentialSANScrosssection 11
configurationaswellasanaverageoverboththeisotopedistributionandthenuclearspinorientations,whicharerandomfornot-too-largefieldsandlowtemperatures(see Section2.4forfurtherdetails).
Atthispointitisimportanttorealizethatforsmall-anglescatteringthediscrete atomicstructureofmanycrystallinematerialsisgenerallyofnoimportance.Often, theprobingneutronwavelengthislargerthantwicethemaximumlattice-planedistanceforallowedreflectionsfromthecrystalstructure(so-calledBraggcutoff).The resolutionrangeoftheconventionalSANStechniquerangesbetweenafewanda fewhundrednanometers.SANScanthereforebedescribedwithinacoarse-grained pictureoftheactualdiscreteatomicstructureofmatter.FornuclearSANS,therelevantcoarse-grainedvariableisthescalarscattering-lengthdensity N (r)(inm 2,and nottobeconfusedwiththenumber N ofnucleiormagneticmomentsinasample). Thisquantityisassumedtobeasmoothandcontinuousfunctionoftheposition r = {x,y,z} insidethematerial.Itisthereforepermissibletoreplacethediscretesum ineqn(1.24)byanintegralover N (r).Thefinalresultforthemacroscopicnuclear SANScrosssectionthenreads(e.g.,[2]):
where N (q)denotestheFouriertransformof N (r),andtheintegralistakenoverthe volume V ofthesample.InSection2.4.3,wewillseehow dΣnuc/dΩcanberelatedto theFouriertransformoftheautocorrelationfunctionof N (r).
NuclearSANS(andSAXS)isnotfurtherconsideredhere,andwereferthereader toSection2.4forasummaryofthebasics.Beforemovingontothediscussionofthe magneticSANScrosssection,andwithrespecttopolarizedneutronscattering,we emphasizethatthenuclearSANScontributionwhichisrelatedtothespinsofthe atomicnucleigivesrisetoa q-independentincoherentbackgroundcontribution.Itis ignoredinthisbook,simplybecausetherelatedscatteringsignalisusuallysmallwhen comparedtothemagneticSANSthatisduetotheelectronicspinsofnonhydrogenated magneticmaterials.
1.4.2MagneticSANScrosssection
Magneticneutronscatteringoriginatesfromtheinteractionbetweenthemagnetic momentoftheneutronandthemagneticfieldthatiscreatedbythespinandthe orbitalmotionofatomicelectrons.Incontrasttothenuclearinteraction[eqn(1.21)], magneticscatteringisanisotropic.Theinteractionpotentialformagneticneutron scatteringisgivenby[76]:
denotesthemagneticdipolemomentoftheneutron, γn =1 913isthemagnetic momentoftheneutronexpressedinunitsofthenuclearmagneton[104],and σP is thePaulispinoperatorfortheneutron.Thequantity
isthemagneticfieldattheposition r thatisproducedbythespin(BS)andthe orbital(BL)motionofanelectronpossessingamagneticmoment µe = 2µBS anda linearmomentum p (µ0:permeabilityoffreespace; µB:Bohrmagneton; S:electronspinoperatorinunitsof ).Notethateqn(1.26)representsonlytheleadingtermin anexpansionoftheelectromagneticneutron-sampleinteractionpotentialinpowers of me/mn,where me denotestheelectronmass[76].Higher-ordercontributions,e.g., duetothescatteringbytheatomicelectricfield[105],areseveralordersofmagnitude smallerthanthe µn · B termandcanbeignoredforthepurposeofthisbook[75].
BasedontheworkbyBloch[106,107],Schwinger[108],andinparticularbyHalpern andJohnson[109],thetheoryofpolarizedthermalneutronscatteringoncondensed matterhasbeenlargelydevelopedbyMaleevetal.[110–112]andBlume[113]inthe early1960s.Theseso-calledBlume–Maleevequationsarecommonlyformulatedin termsofdiscreteatomicspinsratherthaninthecontinuumpicture,asisappropriate formagneticSANS.Wethereforewritedownfirstthegeneralexpressionfortheelastic magneticdifferentialscatteringcrosssectionanddiscusssubsequentlytheapproximationsnecessaryinordertoobtainthemagneticSANScrosssection.Inadditiontothe standardreferences[76,86,103],werecommendthepapersbyIzyumov,deGennes, andMaleev[114–116]fordetailedaccountsofpolarizedmagneticneutronscattering.
Foranunpolarizedincidentneutronbeam,themacroscopicelasticmagneticdifferentialscatteringcrosssectionatscatteringvector q duetoanarrangementof N atomicmagneticmoments µa atpositions rk isgivenby[76,104,117]:
where bm istheatomicmagneticscatteringlength,whichissometimesdenotedwith thesymbol p [104,117],and
istheHalpern–Johnsonvector[109](alsodenotedasthemagneticinteractionor magneticscatteringvector).Thisquantitydependsontheunitscatteringvector ˆ q = q/q = {ˆ qx, ˆ qy , ˆ qz } andontheunitvector ˆ mk = µa,k/µa,k inthedirectionof amagneticmoment.Thespecialdependencyof Qk on ˆ q andon ˆ mk impliesthatfor magneticneutronscatteringonlythecomponentofthemagnetizationwhichisperpendiculartothescatteringvectorisofrelevance(compareFig.2.17).Thisreflectsthe dipolarnatureoftheneutron-magneticinteraction.Theatomicmagneticscattering lengthisgivenby[117,118]:
Table1.2 Atomicmagneticscatteringlengths bm intheSANSregime(computedusing eqn(1.31)with f (q)=1),Curietemperatures TC,andatomicmagneticmomentsofvarious elementsexhibitingferromagnetisminbulkform. TC and µa/µB-valuestakenfrom[119,120].
ElementCrystalStructure(atRT)
Gd hcp 2937.6320.57
Tb hcp 2209.3425.18
Dy hcp 8910 3327 84
Ho hcp 2010.3427.87
Er hcp 209 124 53
Tm hcp 327.1419.25
where re =2 818 × 10 15 mdenotestheclassicalradiusoftheelectron,and f (q)is thenormalizedatomicmagneticformfactor.Notethat
inthesmall-angleregion,whichistheapproximationwhichwewilladoptthroughout thisbook.Table1.2providesthe bm-valuesofsomeofthemostimportantelemental magneticmaterials.Ascanbeseen, bm hasthesameorderofmagnitudeasthenuclear scatteringlengthandcanbequitelargefortheheavyrare-earthmetals(seealso Fig.2.11).Equation(1.31)alsodefinestheconstant[104]
Themagnitudeof Qk forasinglemagneticmomentequals
where αk istheangleenlosedbetween ˆ mk and ˆ q.Thissimpleresulthighlightsthe anisotropiccharacterofmagneticneutronscatteringanddemonstratesthat,fora singleuniformlymagnetizeddomain,themagneticscatteringvanishesfor ˆ q ˆ mk and isatmaximumfor ˆ q ⊥ ˆ mk [seeFig.1.12(b)].
AswithnuclearSANS,eqn(1.29)needstobetransformedintoacontinuumpicture.ThequantityofinterestformagneticSANSisthemagnetizationvectorfieldof thesample, M = M(r),which,similarlyto N (r),isassumedtobeasmoothand continuousfunctionof r.Thedefinitionof M (seeSection3.1)entailsthatthisquantityrepresentsanaverageoverthethermalfluctuationsofmanyindividualatomic