FluidDynamics
Part3:BoundaryLayers
AnatolyI.Ruban
DepartmentofMathematics
ImperialCollegeLondon
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries
c AnatolyI.Ruban2018
Themoralrightsoftheauthorhavebeenasserted
FirstEditionpublishedin2018
Impression:1
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica
BritishLibraryCataloguinginPublicationData Dataavailable
LibraryofCongressControlNumber:2013953774
ISBN978–0–19–968175–4 DOI10.1093/oso/9780199681754.001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
Preface
ThisisPart3ofabookseriesonfluiddynamicsthatcomprises thefollowingfour parts:
Part1. ClassicalFluidDynamics
Part2. AsymptoticProblemsofFluidDynamics
Part3. BoundaryLayers
Part4. HydrodynamicStabilityTheory
Theseriesisdesignedtogiveacomprehensiveandcoherentdescriptionoffluiddynamics,startingwithchaptersonclassicaltheorysuitableforanintroductoryundergraduatelecturecourse,andthenprogressingthroughmoreadvancedmaterialuptothe levelofmodernresearchinthefield.Ourmainattentionison high-Reynolds-number flows,bothincompressibleandcompressible.Correspondingly,thetargetreadergroups areundergraduateandMScstudentsreadingmathematics,aeronauticalengineering, orphysics,aswellasPhDstudentsandestablishedresearchersworkinginthefield.
InPart1,westartedwithdiscussionoffundamentalconceptsoffluiddynamics, basedonthe continuumhypothesis.Wethenanalysedtheforcesactinginsideafluid, anddeducedtheNavier–Stokesequationsforincompressibleandcompressiblefluidsin Cartesianandcurvilinearcoordinates.Thesewereemployedtostudythepropertiesof anumberofflowsthatarerepresentedbytheso-called exactsolutions oftheNavier–Stokesequations.Thiswasfollowedbydetaileddiscussion ofthetheoryofinviscidflows forincompressibleandcompressiblefluids.Whendealingwithincompressibleinviscid flows,aparticularattentionwaspaidtotwo-dimensionalpotentialflows.Thesecan bedescribedintermsofthe complexpotential,allowingforthefullpowerofthe theoryoffunctionsofcomplexvariabletobeemployed.Wedemonstratedhowthe methodofconformalmappingcanbeusedtostudyvariousflows ofinterest,such asflowspast Joukovskiiaerofoils andseparatedflows.Forthelaterthe Kirchhoff model wasadopted.ThefinalchapterofPart1wasdevotedtocompressibleflowsof aperfectgas,includingsupersonicflows.Particularattentionwasgiventothetheory ofcharacteristics,whichwasused,forexample,toanalyse the Prandtl–Meyerflow overabodysurfacewithabendoracorner.Thepropertiesofshockwaveswerealso discussedindetailforsteadyandunsteadyflows.
InPart2weintroducedthereaderto asymptoticmethods.Alsotermedthe perturbationmethods,theyarenowaninherentpartoffluiddynamics.Westartedwith adiscussionofthemathematicalaspectsoftheasymptotictheory.Thiswasfollowed byanexpositionoftheresultsofapplicationoftheasymptotictheorytovariousfluiddynamicproblems.Thefirstofthesewasthe thinaerofoiltheory forincompressible andsubsonicflows,steadyandunsteady.Inparticular,itwasshownthatthistheory allowedtoreducethetaskofcalculatingtheliftforcetoasimpleintegral.Wethen turnedtosupersonicflows.Wefirstanalysedthelinearapproximationtothegoverning
Eulerequations,whichledtoaremarkablysimplerelationshipbetweentheslopeof theaerofoilsurfaceandthepressure,knownasthe Ackeretformula.Wethenconsideredthesecond-order Buzemannapproximation,andperformedanalysisofarather slowprocessofattenuationoftheperturbationsinthefarfield.Part2alsocontains adetaileddiscussionofthepropertiesofinviscid transonic and hypersonicflows.We concludedPart2withanalysisofviscouslow-Reynolds-numberflows.Twoclassical problemsofthelow-Reynolds-numberflowtheorywereconsidered:theflowpasta sphereandtheflowpastacircularcylinder.Inbothcases,theflowanalysisledtoa difficulty,knownas Stokesparadox.Weshowedhowthisparadoxcouldberesolved usingtheformalismofmatchedasymptoticexpansions.
ThepresentPart3isconcernedwiththehigh-Reynolds-numberfluidflows.In Chapter1weconsideraclassofflowsthatcanbedescribedintheframeworkof classicalboundary-layertheory.TheseincludetheBlasiusflowpastaflatplateand theFalkner–Skansolutionsfortheflowpastawedge.WealsodiscussChapman’sshearlayerflowandSchlichting’ssolutionforthelaminarjet.Amongotherexamplesare Tollmien’ssolutionfortheviscouswakebehindarigidbody andtheperiodicboundary layeronthesurfaceofarapidlyrotatingcylinder.Thisisfollowedbyadiscussionof thepropertiesofcompressibleboundarylayers,including hypersonicboundarylayers. Thelatterareinfluencedbytheinteractionwithinviscidpartoftheflow,andinvolve extremelystrongheatingofthegasnearthebodysurface.
Wethenturnourattentiontoseparatedflows.Chapter2considerstwoexamples oftheboundary-layerseparation.Thefirstistheso-called self-inducedseparation of theboundarylayerinsupersonicflow.Thetheoryofself-inducedseparationisbased ontheconceptof viscous-inviscidinteraction,whichwasputforwardasaresultof detailedexperimentalexaminationoftheseparationprocess.Experimentsrevealed anumberofunexpectedeffects.Mostdisputedwastheeffectof upstreaminfluence throughtheboundarylayer.Sinceitcouldnotbeexplainedintheframeworkof theclassicalboundary-layertheory,itwassuggestedthat neartheseparation,the boundarylayercomesinto‘stronginteraction’withinviscidpartoftheflow.InChapter2wepresentmathematicaltheoryoftheviscous-inviscidinteraction,knownasthe triple-decktheory,followingtheoriginalpapersofNeiland(1969a)andStewartsonand Williams(1969)wherethistheorywasformulatedbasedontheasymptoticanalysis oftheNavier–StokesequationsatlargevaluesoftheReynoldsnumber.
ThesecondproblemdiscussedinChapter2istheclassicalproblemoftheboundarylayerseparationfromasmoothbodysurfaceinhigh-Reynolds-numberflowofan incompressiblefluid.Theasymptotictheoryforthisclassofseparatedflowswasput forwardbySychev(1972).Hedemonstratedthat,inordertoresolvethelong-standing contradictionassociatedwithGoldstein’s(1948)singularityattheseparationpoint, onehastoaccountforastronginteractionbetweentheboundarylayerandinviscid flowneartheseparation.Interestinglyenough,thisinteractiondevelopsnaturallyin responsetothesingularityintheclassicalKirchhoffmodel forinviscidseparatedflows.
Chapter3isdevotedtotheflowofanincompressiblefluidnear thetrailingedgeof aflatplate.Accordingtotheclassicalboundary-layertheory,theflowpastaflatplate isdescribedbytheBlasiussolution.However,ithasbeenfoundtofailnearthetrailing edgewheretheboundarylayeragaincomesintointeractionwiththeinviscidpartof
Preface vii
theflow.Stewartson(1969)andMessiter(1970)werethefirst todemonstratethatin thevicinityofthetrailingedge,theflowisdescribedbythe triple-decktheory.The readerwillseethattheviscous-inviscidinteractionchangestheflownearthetrailing edge,andleadstoanoticeableincreaseoftheviscousdragforceactingontheplate.
Chapter4concernssubsonicandsupersonicflowsnearcorner pointsofthebody surface,whereincreasingthecornerangleallowsustoobservethetransitionfroman attachedflowtoaflowwithlocalseparationintheboundarylayer.
Finally,inChapter5wepresentthe MarginalSeparationtheory.Itisaspecial versionofthetriple-decktheorydevelopedbyRuban(1981, 1982)andStewartson etal. (1982)forthepurposeofdescribingtheboundary-layerseparationattheleading edgeofanaerofoil.Theseparationassumestheformoftheso-called‘shortseparation bubble’thatisobservedto‘burst’whentheangleofattackreachesacriticalvalue. Asaresult,theliftforcedecreasesdramatically—thisphenomenonisknownasthe leading-edgestall.
Thematerialpresentedinthisbookisbasedonlecturecoursesgivenbytheauthor attheMoscowInstituteofPhysicsandTechnology,theUniversityofManchester,and ImperialCollegeLondon.
1.9.1Problemformulation
1.9.2Crank–Nicolsonmethod
1.11HypersonicBoundaryLayers 110
1.11.1Hypersonicflowpastabodywitharoundednose110
1.11.2Hypersonicboundarylayersonthinbodies114
1.11.3Upstreaminfluencethroughhypersonicboundarylayers128 Exercises8 138
2Boundary-LayerSeparation 143
2.1ExperimentalEvidence 143
2.2Self-InducedSeparationofSupersonicBoundaryLayer149
2.2.1Formulationoftheproblem 149
2.2.2Theflowupstreamoftheinteractionregion150
2.2.3Inspectionanalysisoftheinteractionprocess151
2.2.4Triple-deckmodel 157
2.2.5Upstreaminfluence 170
2.2.6Flowbehindtheinteractionregion174
2.2.7Canonicalformoftheinteractionproblem186 Exercises9 189
2.3IncompressibleFlowSeparationfromaSmoothBodySurface193
2.3.1Problemformulation 194
2.3.2Flowoutsidetheinteractionregion195
2.3.3Boundarylayerbeforetheinteractionregion202
2.3.4Viscous-inviscidinteraction 210
2.3.5Flowbehindtheinteractionregion223
2.3.6Canonicalformoftheinteractionproblem230 Exercises10 234
3Trailing-EdgeFlow 242
3.1ProblemFormulation 242
3.2Goldstein’sWake 245
3.2.1Viscoussublayer(region2d)247
3.2.2Mainpartoftheboundarylayer(region2c)250
3.3PerturbationsintheInviscidFlow 252
3.4Second-OrderPerturbationsintheBoundaryLayer256
3.4.1Viscoussublayer(region2a)257
3.5Triple-DeckModel 260
3.5.1Viscoussublayer(region3) 261
3.5.2Middletier(region4) 264
3.5.3Uppertier(region5) 267
3.5.4Interactionproblemandnumericalresults269 Exercises11 272
4IncipientSeparationNearCorners 279
4.1ProblemFormulation 279
4.2SubsonicFlow 280
4.2.1Inviscidflowregion 281
4.2.2Boundarylayerbeforethecorner283
4.2.3Viscous-inviscidinteractionregion290
4.2.4Interactionproblem
4.3SupersonicCompressionRampFlow303
4.3.1Linearproblem
4.3.2Numericalsolutionofthenonlinearproblem310
5MarginalSeparationTheory
5.1ExperimentalObservations
5.2InviscidFlowRegion
5.3BoundaryLayer
5.3.1Theoreticalanalysisoftheboundarylayer323
5.3.2Goldstein’ssingularity
5.3.3Weaksingularity
5.3.4Formationofthesingularityintheboundarylayer336
5.4Viscous-InviscidInteraction
5.4.1Upperlayer(region5)
5.4.2Viscoussublayer(region3)
5.4.3Mainpartoftheboundarylayer(region4)357
5.4.4Viscous-inviscidinteractionproblem358
5.4.5Numericalresults
Introduction
Thenotionofthe boundarylayer wasfirstintroducedbyPrandtl(1904)inhis seminalpaperreadbeforethe3rdInternationalMathematicsCongressinHeidelberg. Inthiswork,Prandtlwasconcernedwithsomeparadoxicalresultsofthetheoryof high-Reynolds-numberflows.Ifthefluidviscosityisverysmall,thenitmightseem obviousthattheNavier–Stokesequationsgoverningthefluidmotioncouldbereplaced bytheirinviscidcounterparts,theEulerequations.Thelatterareknowntodescribe variouspropertiesoffluidmotionperfectlywell.Inparticular,theEulerequations maybeusedtocalculatetheliftforceproducedbyanaerofoil.However,theyfail completelyincalculatingthedrag.Accordingtotheinviscidflowtheory,thedragof anaerofoilinasteadyflowisalwayszero.Thisresultisknownasthe d’Alembert paradox.Itisapplicablenotonlytoaerofoils,butalsotootherbodyshapes.For example,thesolutionoftheEulerequationsfortheflowofan incompressiblefluid pastacircularcylinderiswrittenintermsofthecomplexpotential w(z)as1
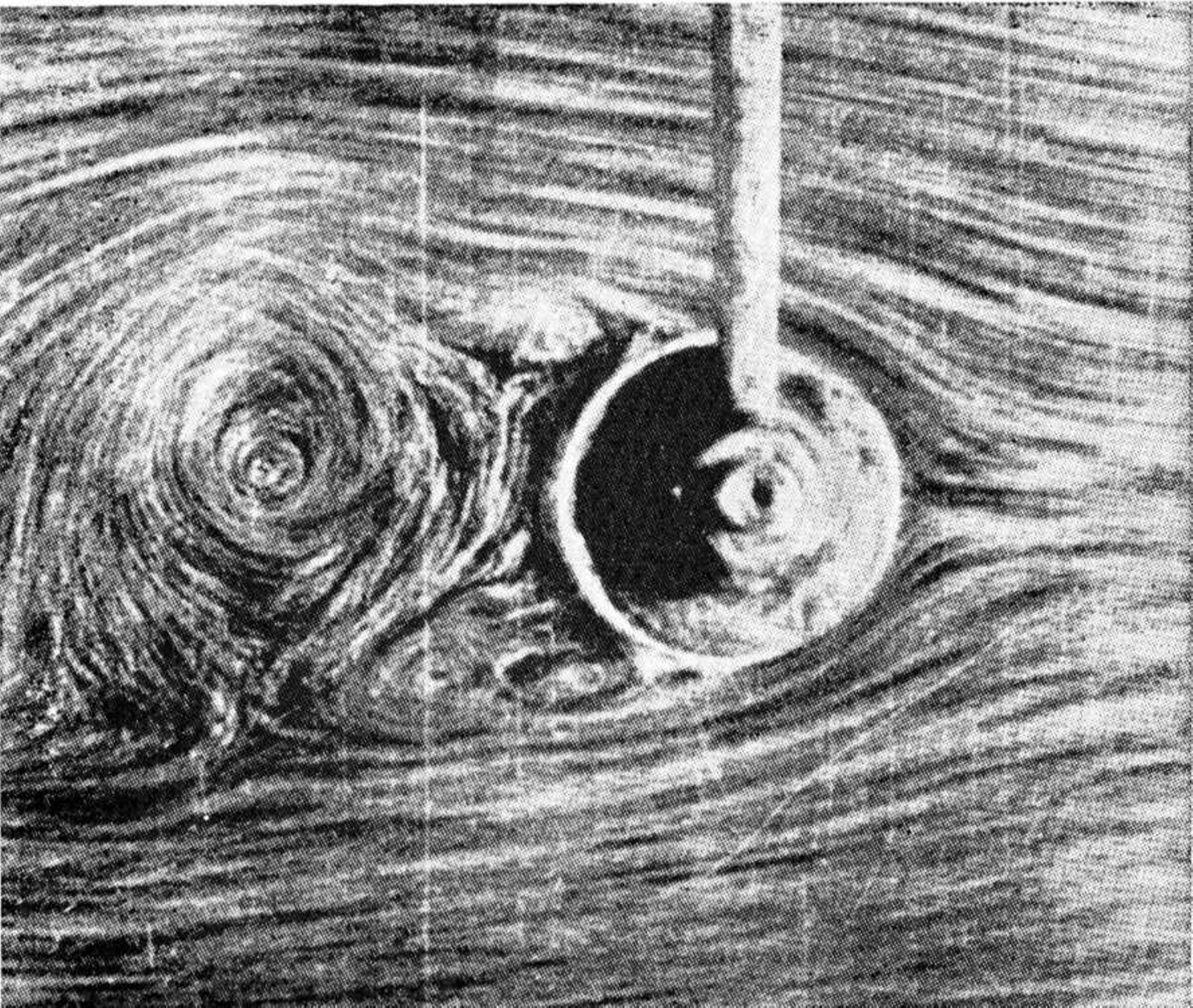
Here V∞ isthefree-streamvelocity, a isthecylinderradius,and z = x + iy,with x and y beingCartesiancoordinates.FigureI.1(a)showsthestreamlinepatternplotted usingthissolution.ItiscontrastedinFigureI.1(b)withanexperimentalvisualization oftheflowpastacircularcylinder.Clearly,thereisasignificantdifferencebetween thetheoryandtherealflow.WhiletheEulerequationsadmitthesolutionwherethe fluidparticlesgosmoothlyaroundthecylinderandflowremainsfullyattachedto thecylindersurface,therealflowdevelopsaseparationthatleadstoaformationof recirculationeddiesbehindthecylinder.
Toexplaintheseobservations,Prandtl(1904)suggestedthat,atlargevaluesof theReynoldsnumber,theflowfieldaroundarigidbodyhastobe dividedintotwo distinctregions:themainpartoftheflowandathinboundary layerthatformsalong thebodysurface.Themainpartoftheflowmaybetreatedasinviscid.However,forall Reynoldsnumbers,nomatterhowlarge,theviscousforcesmaintaintheirimportance intheboundarylayer.AccordingtoPrandtl,itisduetospecificbehaviouroftheflow intheboundarylayerthatseparationtakesplace.
AnimmediateoutgrowthofPrandtl’sworkwasthedevelopmentofthe classical boundary-layertheory thatinspiredmuchofresearchofhigh-Reynolds-numberflows inthefirsthalfofthetwentiethcentury.Thesestudieswere mainlyconcernedwith situationwheretheboundarylayerremainedattachedtothe bodysurface.AnexpositionoftheresultsofthistheoryisgiveninChapter1ofthis book.TheninChapter2 weturntotheanalysisofseparatedflows.Prandtldescribed theseparationprocess
1Seeequation(3.4.28)onpage166inPart1ofthisbookseries.
FluidDynamics:Part3:BoundaryLayers c AnatolyI.Ruban,2018.Published2018by OxfordUniversityPress.10.1093/oso/9780199681754.001.0001
(a)Theoreticalpredictions. (b)Experimentalobservations;theflowis fromrighttoleft.
Fig.I.1:Comparisonoftheoreticalpredictionsfortheflow pastacircularcylinder withexperimentalobservationsbyPrandtlandTietjens(1934).
asfollows.Sincetheflowintheboundarylayerhastosatisfy theno-slipcondition onthebodysurface,thefluidvelocitydecreasesfromthevaluedictatedbytheinviscidtheoryattheouteredgeoftheboundarylayertozeroonthebodysurface.The slow-movingfluidnearthebodysurfaceisverysensitivetopressurevariationsalong theboundarylayer.Ifthepressuredecreasesdownstream,thentheboundarylayer remainsattachedtothebodysurface.Thissituationisobservedonthefrontpartof thebody;seeFigureI.1.However,furtherdownstreamthepressurestartstorise,and theboundarylayertendstoseparatefromthebodysurface.Thereasonforseparation isthatthekineticenergyoffluidparticlesinsidetheboundarylayerappearstobeless thanitisattheouteredgeoftheboundarylayer.Thismeansthat,whilethepressure riseintheouterflowmaybequitesignificant,thefluidparticlesinsidetheboundary layermaynotbeabletogetoverit.Evenasmallincreaseofpressuremaycausethe fluidparticlesnearthewalltostopandthenturnbacktoform areverseflowregion characteristicofseparatedflows.
Itmightseemsurprisingthattheclearunderstandingofthe physicalprocesses leadingtotheseparation,couldnotbeconvertedintoarationalmathematicaltheory formorethanhalfacentury.Thefactisthattheclassicalboundary-layertheory,as presentedbyPrandtl,isbasedontheso-called hierarchicalapproach,whentheouter inviscidflowiscalculatedfirst,ignoringtheexistenceoftheboundarylayer,andthen theflowintheboundarylayerisanalysed.Bythelate1940s,itbecameclearthatsuch astrategyleadstoamathematicalcontradictionassociatedwithsingularbehaviour oftheboundarylayer.Forthesteadyflowpastasolidwall,thissingularityisreferred toasthe Goldsteinsingularity.ThissingularitywasfirstdescribedbyLandauand Lifshitz(1944),whodemonstratedthattheshearstressonthebodysurfaceupstream ofseparationdropsasthesquareroot √s ofthedistance s fromtheseparation,andthe velocitycomponentnormaltothesurfacetendstoinfinitybeinginverselyproportional to √s.Thisresultwaslaterconfirmedbasedonmorerigorousmathematicalanalysis byGoldstein(1948).Goldsteinalsoprovedthatthesingularityatseparationprecludes
apossibilityofcontinuingthesolutionbeyondtheseparationpointintotheregionof reverseflow.
Simultaneously,anotherimportantdevelopmenttookplace.Duringthe1940sand 1950s,asignificantbodyofexperimentalevidencewasproducedwhichshowedthat theboundary-layertheoryinitsclassicalformwasinsufficientfordescribingtheseparationphenomenon.Mostdisputablewastheeffectofupstreaminfluencethroughthe boundarylayerinasupersonicflowpriortoseparation.Itcouldnotbeexplainedin theframeworkoftheclassicalboundary-layertheory,andledtoaconceptof viscousinviscidinteraction;see,forexample,Chapman etal. (1958).Theasymptotictheory ofviscous-inviscidinteraction,knownnowasthe triple-decktheory,wasformulated simultaneouslybyNeiland(1969a)andStewartsonandWilliams(1969)inapplication tothephenomenonof self-inducedseparation oftheboundarylayerinasupersonic flow,andbyStewartson(1969)andMessiter(1970)inapplicationtoincompressible fluidflownearthetrailingedgeofaflatplate.Twoyearslater,usingtheconceptof viscous-inviscidinteraction,Sychev(1972)wasabletoresolvethecontradictionassociatedwithGoldstein’ssingularityattheseparationpoint,andcreatedtheasymptotic theoryoflaminarboundary-layerseparationfromasmoothbodysurface,e.g.,acircularcylinder,inanincompressiblefluidflow.
Soonafterthat,itbecameclearthattheviscous-inviscidinteractionplaysakeyrole inmanyfluid-dynamicphenomena.Chapters2–5provideanexpositionofapplication ofthetheorytovariousseparatedflows.WewillalsousethetheoryinPart4ofthis bookseries.Thereaderwillseethattheviscous-inviscidinteractionisinstrumentalin thedevelopmentofinstabilitiesoftheboundarylayerandtransitiontoturbulence.
1.1FlowPastaFlatPlate
Letusconsidertwo-dimensionalsteadyviscousflowpastaflatplatealignedwith theoncomingflow.Weshallsupposethatthefluidisincompressible,and,therefore, thedensity ρ andkinematicviscositycoefficient ν remainconstantallovertheflow field.Wedenotetheplatelengthby L andintroduceCartesiancoordinates(ˆx, ˆ y) withˆ x measuredalongtheflatplatesurfacefromitsleadingedge O,andˆ y inthe perpendiculardirectionasshowninFigure1.1.Withthevelocitycomponentsdenoted by(ˆu, ˆ v)andthepressurebyˆ p,theNavier–Stokesequationsarewrittenas1
Theboundaryconditionsfortheseequationsaretheno-slip conditionsthatshould beappliedonbothsidesoftheplate,
andthefree-streamconditions
Here V∞ and p∞ arethefluidvelocityandpressureinthefree-stream,respectively.
1Seeequations(1.7.6)onpage62inPart1.Weassumeherethatbodyforce f isnegligible.
FluidDynamics:Part3:BoundaryLayers c AnatolyI.Ruban,2018.Published2018by OxfordUniversityPress.10.1093/oso/9780199681754.001.0001
Fig.1.1:Problemlayout.
Inordertoexpressequations(1.1.1)andboundaryconditions(1.1.2),(1.1.3)in non-dimensionalform,weperformthefollowingtransformationofthevariables:
ThisturnstheNavier–Stokesequations(1.1.1)into
Theno-slipconditions(1.1.2)become
andthefree-streamconditions(1.1.3)assumetheform
TheReynoldsnumber Re isdefinedas
andourtaskwillbetofindtheasymptoticsolutiontotheproblem(1.1.5)–(1.1.7)as Re →∞. Clearly,wearedealingherewithasingularperturbationproblem.2 Infact,the basicideasthatlieinthefoundationofthemethodofmatchedasymptoticexpansions
2SeeSections1.3and1.4inPart2ofthisbookseries.
Chapter1.ClassicalBoundary-LayerTheory
werefirstputforwardbyPrandtl(1904)inhisseminalpaperreadbeforethe3rd InternationalMathematicsCongressinHeidelberg,whereheintroducedthenotion ofthe boundarylayer.PrandtlarguedthatatlargevaluesoftheReynoldsnumber Re,almosttheentireflowfieldcanbetreatedasinviscid.Still,atany Re,nomatter howlarge,therealwaysexistsathinlayeradjacenttothebodysurface,termedthe boundarylayer,wheretheroleofinternalviscosityremainsofprimaryimportance.
1.1.1Asymptoticanalysisoftheflow
Weshallstartwiththe outerregion,wherebothcoordinates x and y areoftheorder oftheplatelength.Inthenon-dimensionalvariables,this iswrittenas x = O(1),y = O(1),Re →∞.
TheouterregionisshowninFigure1.2asregion1,andinwhat follows,weshallrefer toitasthe externalflowregion
ThesolutionoftheNavier–Stokesequations(1.1.5)inthis regionwillbesoughtin theformoftheasymptoticexpansions3 u(x,y; Re)= u0(x,y)+ ,v(x,y; Re)= v0(x,y)+ , p(x,y; Re)= p0(x,y)+ ···
(1.1.8)
Substituting(1.1.8)into(1.1.5)andsetting Re →∞,wefindthatfunctions u0, v0, and p0 satisfytheEulerequations:
(1.1.9)
UnliketheNavier–Stokesequations(1.1.5),theEulerequations(1.1.9)donotinvolve thesecondorderderivativesofthevelocitycomponents,andthereforetheycannot
Fig.1.2:Inviscidflow(region1).
3Herewerestrictourattentiontotheleading-orderterms.
1.1.FlowPastaFlatPlate 7
besolvedwiththeentiresetoftheboundaryconditions(1.1.6),(1.1.7).According totheinviscidflowtheory,theEulerequationsarecompatiblewiththefree-stream conditions
andtheimpermeabilityconditionontherigidbodysurface. Fortheflatplateitis writtenas
Aninfinitelythinflatplatedoesnotproduceanyperturbationsinaninviscidflow and,indeed,bydirectsubstitution,itiseasilyverifiedthat
isasolutiontotheboundary-valueproblem(1.1.9)–(1.1.11).
Aswasexpected,theoutersolution(1.1.12)doesnotsatisfytheconditionfor u in (1.1.6).Hence,aninnerregionoccupyingasmallvicinityoftheplatesurfaceshould bebroughtintoconsideration.Thisnewregionisshownasregion2inFigure1.3. Sincetheboundarylayeristhin,wehavetoscalethecoordinatenormaltothewall:
Here δ(Re)issupposedsmall,thatis
Astheboundarylayerextendsalongtheentiresurfaceofthe flatplate,noscalingof thelongitudinalcoordinate x isrequired.Consequently,theasymptoticanalysisofthe Navier–Stokesequations(1.1.5)inregion2hastobebasedonthelimit
Chapter1.ClassicalBoundary-LayerTheory
Correspondingly,theleading-ordertermsoftheasymptoticexpansionsof u, v,and p inthisregionwillbesoughtintheform
Hereithasbeentakenintoaccountthatthelongitudinalvelocitycomponent u decreasesfrom u =1attheouteredgeoftheboundarylayerto u =0onthewall, whichsuggeststhat u isanorderonequantity.Thecoefficients σ(Re)and χ(Re)in theasymptoticexpansionsof v and p arenotknowninadvance.Weexpecttofind theminthecourseofanalysisoftheNavier–Stokesequations.
Letusstartwithcontinuityequation(1.1.5c).Thesubstitutionof(1.1.15)intothis equationyields
Accordingtotheprincipleofleastdegeneration,wehaveto choose4
andthecontinuityequationtakestheform
Letusnowconsiderthelongitudinalmomentumequation(1.1.5a).Thesubstitutionof(1.1.15)into(1.1.5a)yields
Weseethatthesecondtermontheright-handsideof(1.1.18) issmallcomparedto anyofthetermsontheleft-handside,andshouldbeneglectedas Re →∞.Asfaras thethirdtermisconcerned,itcanberetainedintheequationbysetting
4Indeed,ifweassumed δ(Re) ≫ σ(Re),whichcouldbeinterpretedasanattempttoconsidera regionwithathicknessmuchlargerthanthethicknessoftherealboundarylayer,thenthecontinuity equationwoulddegenerateto ∂U0 ∂x =0.
Sinceupstreamofthetrailingedge u =1,itwouldleadtoaconclusionthat U0 ≡ 1,asifwestill weredealingwiththeouterinviscidregion.
If,ontheotherhand, σ(Re)wasassumedmuchlargerthan δ(Re),whichcouldbeinterpreted asanoverestimationoftheorderofmagnitudeof v in(1.1.15),thenthecontinuityequationwould degenerateto
∂V0 ∂Y =0
With V0 =0ontheplatesurface,thesolutionoftheaboveequationis V0 =0, whichmeansthattheasymptoticexpansionfor v in(1.1.15)doesnotreallyhaveatermwith σ larger than δ.
Thischoicecanbejustifiedwiththehelpofthefollowingarguments.Ifoneassumes that δ2Re ≫ 1,thentheflowwouldappearinviscid,andtheno-slipcondition U0 =0 ontheplatesurfacecouldnotbesatisfied.If,ontheotherhand, δ2Re ≪ 1,then equation(1.1.18)degeneratesto
Ithastobesolvedwiththeno-slipconditionontheplatesurface,
andthecondition
whichfollowsfrommatchingoftheasymptoticexpansionfor u in(1.1.15)withthe solution(1.1.12)inregion1.Clearly,theboundary-value problem(1.1.20)–(1.1.22) doesnothaveasolution.
Thisconfirms,onceagain,thattheprincipleofleastdegenerationprovidesthe onlypossiblechoiceof δ(Re)asgivenby(1.1.19).Using(1.1.19),wecanwritethe longitudinalmomentumequation(1.1.18)as
Itremainstodetermine χ(Re),forwhichpurposeweshallusethelateralmomentumequation(1.1.5b).Thesubstitutionof(1.1.15),(1.1.13),(1.1.16),and(1.1.19) into(1.1.5b)yields
Whendealingwithequations(1.1.23)and(1.1.24),weshall considerthefollowing twooptions.Ifweassumethat χ(Re)issmall,thatis, χ → 0as Re →∞,thenthe equation(1.1.23)reducesto
If,ontheotherhand, χ(Re)= O(1)or χ(Re) ≫ 1,thenitfollowsfrom(1.1.24)that
Aboundaryconditionforthisequationmaybededucedbycomparingtheasymptotic expansionsforthepressureinregions1and2;thesearegivenby(1.1.8)and(1.1.15), respectively.Keepinginmindthatthesolutioninregion1isgivenby(1.1.12),one canseethatforany χ(Re)= O(1)or χ(Re) ≫ 1,thematchingconditioniswritten as
Solving(1.1.26)withthiscondition,wecanconcludethat P0 =0everywhereinside theboundarylayer,whichmeansthatthepressuregradientshouldbedisregardedin thelongitudinalmomentumequation(1.1.23),reducingitagainto(1.1.25).
Chapter1.ClassicalBoundary-LayerTheory
Equation(1.1.25)involvestwounknownfunctions, U0 and V0.Beingcombined withthecontinuityequation(1.1.17),itformsaclosesetofequations,whichserveto determinethevelocityfield U0,V0 intheboundarylayer.Now,weneedtoformulate theboundaryconditionsfor(1.1.25),(1.1.17).Achoiceof theboundaryconditions, whicharecompatiblewithaparticularpartialdifferential equation,dependsonthe typeoftheequation.Thelatterisdeterminedbythehigherorderderivativesinthe equationconsidered.Ifwestartwiththemomentumequation (1.1.25),thenwecansee thatthehigherorderderivativeof U0 withrespectto Y isrepresentedbytheviscous term, ∂2U0/∂Y 2,ontheright-handsideof(1.1.25).Theequationalsoinvolvesthe firstorderderivativeof U0 withrespectto x intheconvectiveterm U0 ∂U0/∂x onthe left-handsideoftheequation.Thissuggeststhatthemomentumequation(1.1.25)is parabolic.
Aclassicalexampleofaparabolicequationistheheat-transferequation.When applied,say,toaheat-conductingrod,itmaybewrittenas
Here, a isapositiveconstantthatrepresentsthethermalconductivityofthematerial therodismadeof, T isthetemperaturetobefound, t isthetime,and x isthe coordinatemeasuredalongtherod.Thelatterisassumedtooccupytheinterval x ∈ [0,d]ofthe x-axis,asshowninFigure1.4.Inordertodeterminethetemperature T at apoint= x0 insidetherod,attime t = t0,itisnecessarytospecifythetemperature distributionalongtherodatinitialinstant t =0,andalsotoformulatethethermal conditionsattherodendsfor t ∈ [0,t0].Theseboundariesareshownbybracesin Figure1.4.Thesolutionatpoint(t0,x0),obviously,doesnotdependontheboundary conditionsattherodendsatlatertimes t>t0.
Similarly,ifthecoefficient U0 inthefirsttermontheleft-handsideof(1.1.25) ispositive,thentomakethesolutionofthemomentumequation(1.1.25)unique,we
(t0,x0)
t0 t
Fig.1.4:Theboundaryconditionsfortheheat-transferequation(1.1.27).
1.1.FlowPastaFlatPlate 11
need,firstofall,tospecifyinitialdistributionof U0 attheleadingedgeoftheflat plate.Sinceeverywhereupstreamoftheplatetheflowisunperturbed,wehave
U0 =1at x =0,Y ∈ (0, ∞)
Secondly,correspondingtotheboundaryconditionsattherodends,weneedtoformulatetheconditionsfor U0 ontheplatesurface(Y =0)andattheouteredgeofthe boundarylayer(Y = ∞).Thefirstofthese,
U0 =0at Y =0,x ∈ [0, 1], isdeducedbysubstitutingtheasymptoticexpansion(1.1.15)for u intotheno-slip condition(1.1.6).Theboundaryconditionattheouteredge oftheboundarylayer
U0 =1at Y = ∞
followsfrommatchingwiththesolution(1.1.8),(1.1.12)intheouterflowregion. Ifthelongitudinalvelocitycomponent U0 wereknown,thenthelateralvelocity component V0 couldbefoundbyintegratingthecontinuityequation(1.1.17)with respectto Y .Toperformthistask,aninitialconditionfor V0 isneeded.Itisprovided bytheimpermeabilityconditionontheflatplatesurface,
V0 =0at Y
∈ [0, 1]
Summarizingtheaboveanalysis,weseethatthevelocitycomponentsarerepresentedintheboundarylayer(region2)intheformofasymptoticexpansions
wherefunctions U0 and V0 havetobefoundbysolvingthefollowingboundary-value problem.
Problem1.1 Findsolutiontotheequations
subjecttotheinitialconditionattheleadingedgeoftheplate
theno-slipconditionsontheplatesurface U0 = V0 =0 at Y =0,x ∈ [0, 1], (1.1.29d)
andthematchingconditionwiththesolutionintheexternal inviscidflow
1.1.2Blasiussolution
Asymptoticanalysispresentedintheprevioussectionbringsaboutasignificantsimplificationtothemathematicaldescriptionofthehigh-Reynolds-numberflowpastaflat plate.Weseethatthegoverningequationsbecomelesscomplicated,andthelateral momentumequationisnolongerneededwhendeterminingthevelocityfield,(u,v). However,evenmoreimportantisthefactthatthe elliptic Navier–Stokesequations (1.1.5)arereducedtotheboundary-layerequations(1.1.29a),(1.1.29b),whichare parabolic,and,therefore,possessthefollowingproperty.Provided thatthecoefficient U0 before ∂U0/∂x inthefirsttermontheleft-handsideof(1.1.29a)ispositiveeverywhereexceptonthewall,thesolutionofequations(1.1.29a),(1.1.29b)atanypoint (x0,Y0)intheboundarylayerdependsonlyontheboundaryconditionsupstreamof thispoint, x ≤ x0.Novariationoftheboundaryconditionsdownstreamoftheline x = x0 caninfluencethesolutionat(x0,Y0).Hence,onecansaythateverywhere upstreamofthetrailingedgeoftheplate,theboundarylayer‘doesnotknow’thatthe plateisfinite,andbehavesinthesamewayastheboundarylayeronasemi-infinite flatplate.Sincethesemi-infiniteflatplatedoesnothaveacharacteristiclengthscale, thesolutiontoProblem1.1maybeexpectedtohavea self-similarform.Thismeans thatifdistributionsofvelocitycomponents U0 and V0 acrosstheboundarylayerwere knownatsomelocation,say x =1,thenatanyotherlocation, U0 and V0 couldbe foundusingsimple‘zooming’.Mathematically,thiszoomingisperformedusingaffine transformations.
Letussupposethat
isasolutiontoProblem1.1,and,inparticular,thedistributionsof U
and V0 across theboundarylayerat x =1aregivenbyfunctions
Letusthentrytofindaninvariantaffinetransformationthatleavesequations(1.1.29a), (1.1.29b),andboundaryconditions(1.1.29c)–(1.1.29e)unchanged.Wewrite
where A, B, C,and D arepositiveconstants.
Thesubstitutionof(1.1.32)into(1.1.29a)and(1.1.29b)gives
whiletheboundaryconditions(1.1.29c)–(1.1.29e)turninto
Toensurethattheequationsandtheboundaryconditionsremainunchanged,onehas toset
Solvingtheseequationswefind
with C remainingarbitrary.
Sincethetransformedboundary-valueproblemcoincideswiththeoriginalone,it alsoadmitsthesolution(1.1.30),whichnowshouldbewrittenas
Using(1.1.32)and(1.1.33),wecanexpress(1.1.34)intheform
Here,parameter C mayassumeanarbitraryvalue,andtherefore,maybeconsideredas anadditionalindependentvariable.Inparticular,itmaybechosentocoincidewith x, whichturns(1.1.35)into
Weseethatforany x ∈ (0, 1),thedistributionsof U0 and V0 acrosstheboundary layermaybereducedtothoseatthetrailingedgeoftheplate
Using(1.1.31)in(1.1.36),wearriveataconclusionthatthesolutiontoProblem1.1 maybesoughtintheform
wheretheindependentvariable
isreferredtoasthe similarityvariable.
Inordertofindfunctions f (η)and g(η),wehavetosubstitute(1.1.37),(1.1.38) intotheboundary-layerequations(1.1.29a),(1.1.29b),andtheboundaryconditions (1.1.29c)–(1.1.29e).Itiseasilyseenthat