CovariantPhysics
FromClassicalMechanicsto GeneralRelativityandBeyond
MoatazH.Emam
StateUniversityofNewYorkCollegeatCortland
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries c MoatazH.Emam2021
Themoralrightsoftheauthorhavebeenasserted FirstEditionpublishedin2021
Impression:1
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica BritishLibraryCataloguinginPublicationData Dataavailable
LibraryofCongressControlNumber:2020951689
ISBN978–0–19–886489–9(hbk.)
ISBN978–0–19–886500–1(pbk.)
DOI:10.1093/oso/9780198864899.001.0001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
ToMiriam,Maya,andMourad
Preface
Thisis not “yetanotherbookonthegeneraltheoryofrelativity.”Whilethetheorydidinspire,andindeedplaysamajorrolein,ourdiscussion,itcanbethought ofasonlyonepartofagreaterwhole.Initiallydevelopedasatheoryofgravity,it wasslowlyrealizedthatgeneralrelativityhadadeepermeaningthanjustthat.It teachesus,amongotherthings,acompletelynewunderstandingofspaceandtime, togetherrenamed spacetime:asinglefabricwithitsownparticularsetofsymmetriesandproperties.WhilewelearnthatthefamiliarEuclideangeometry1 thatwe havealllearned(andloved?)inschoolnolongerapplies,wealsodiscoverthatits mostfundamentalsymmetriesarenotlost,butrather“upgraded”tonewanddeeper ones;leadingtoa“spacetime”that’salotmoredynamicandflexiblethantheone welearnedaboutfromEuclid,Galileo,2 orNewton.3 Abyproductofthisdynamical flexibility,prominentingeneralrelativity,isthephenomenonthatwecall“gravity;” butitis only abyproduct.Itisactuallypossible,atleastinprinciple,togothrough anentirecourseongeneralrelativitywithoutmentioningtheword“gravity”once,insteadjustfocusingonitsformalstructureandthesymmetriesitinspires!Clearlysuch achoicewouldnotbeaveryproductiveone,asitmeansthatwewouldbemissingout onwhatisundoubtedlythemostimportantapplicationofthetheory;nevertheless, it is possible.Thetheoryitselfistheculminationoftheeffortsofmanyphysicists andmathematicians,mostnotablyAlbertEinstein,4 HermannMinkowski,5 Hendrik Lorentz,6 HenriPoincar´e,7 DavidHilbert,8 andothers.Einstein,ofcourse,isresponsibleforthemorerevolutionaryideasinthetheory.Todayitisconsideredhisgreatest contributiontophysics,aswellaspossiblythemostamazingsingularachievementby ahumanbeinginhistory.9
1EuclidofAlexandriawasaGreekmathematicianwholivedaroundthethirdcenturyBCE.His book Elements isconsideredthefoundationaltextofmoderngeometryintwo-andthree-dimensional flatspace.Hisaxioms,theorems,andlemmasconstitutethefamiliargeometrytaughttodaytohigh schoolstudents.Theterm“Euclidean,”coinedinhishonor,signifiesflatspace,asopposedto“nonEuclidean,”orcurvedspaces.
2GalileoGalilei:Italianastronomer,physicist,engineer,philosopher,andmathematician(1564–1642).
3SirIsaacNewton:Englishmathematician,physicist,astronomer,theologian,andauthor,requiring perhapsnointroduction(1642–1726).
4Germanphysicist(1879–1955).
5Germanmathematician(1864–1909).
6Dutchphysicist(1853–1928).
7Frenchmathematicianandtheoreticalphysicist(1854–1912).
8Germanmathematician(1862–1943).
9CharlesDarwin’stheoryofnaturalselectionmightbeaclosecontender.
viii Preface
Oneofthemostfundamentalcharacteristicsofthisnewunderstandingofspace andtimethathasarisenfrom,but,onecanargue,hasbecomeevenmoreimportant than,thetheoryofrelativity,iswhatmathematicianssometimescall diffeomorphisminvariance,which,asfarasweareconcerned,canbethoughtofassimplythe“invarianceofthelawsofphysicsbetweencoordinatesystems,”alsoknown as coordinatecovariance,orjust covariance.Thisidea,whichwillbeourmain focusformostofthisbook,liesatthedeepestfoundationsofphysicsandiscertainlytrueinthespecialtheoryofrelativity(specialcovariance),thegeneraltheory(generalcovariance),andevenordinarynon-relativisticphysics,i.e.theusual Euclidean/Galilean/Newtonianworldview(classicalcovariance).Whatitmeansis this:Theuseofanytypeofcoordinatesystemdoes not affectthephysicaloutcome ofanygivenproblem.Aspecificphysicsformulaappliedtosomeproblemshouldgive exactly thesamephysicalanswerswhetheronehasusedCartesiancoordinatesorany othertypeofcoordinatesystem(andtheyarelegion).Thisshouldbeintuitivelytrue eventothebeginner,becausecoordinatesystemsareahumanchoiceandnature shouldnot,andindeeddoesnot,careaboutourchoicesorconventions.Ontheother hand,thewaytheformula looks inCartesiancoordinatesissignificantlydifferentfrom thewayitlooksinothercoordinates.Soanimportantquestiontoaskisthis:Howcan onewritethelawsofphysicsinasingleformthatistruein any coordinatesystem? Inotherwords,inaformthatiscoordinate covariant,yetiseasyenoughtouseonce achoiceofcoordinateshasbeenmade?Inthisbookwewillapproachourstudyof spaceandtimefromtheperspectiveofcovariance;assuch,itisperhapsimportantto understandwhatwemeanbythis,eventhisearlyinthereading.Let’sthenclarify further:ConsiderNewton’ssecondlawasanexample.Itisusuallyfirstencountered inintroductorycoursesinthefollowingform:
= ma, (0.1)
where F isthevectorrepresentingthenetsumofallexternalforcesactingonamass m andresultinginanacceleration a 10 Writteninthisform,eqn(0.1)iscorrectin anycoordinatesystem,i.e.inasenseitis already covariant.Buttoactuallycalculate numericalresultsonestillneedstomakeaspecificchoiceofcoordinateswhichwill necessarilysplittheequationintoitsconstituentcomponentsandhaveaformthat ishighlydependentonthecoordinatesystemused.Forexample,intwo-dimensional Cartesiancoordinates(x,y),Newton’slawreducestothefollowingsetofequations:
x = max Fy = may, (0.2)
where(Fx,Fy)and(ax,ay)aretheCartesiancomponentsoftheforceandacceleration respectively.Withtheknowledgethataccelerationisthesecondderivativeofthe positionwecanwrite
10Wewillmostlydenotevectorsbyboldfacetypefont,exceptwhenthereisapossibilityof confusion.Insuchcaseswewilluseanarrowoverthesymboltodenoteavector;forexample, F
F
F
Preface
orinamorecompactform
whereanoverdotisthestandardnotationforaderivativewithrespecttotime(˙x = dx dt , x = d2 x dt2 ,andsoon).Thisshouldbefamiliareventothereaderwhohasonlyhad anintroductoryphysicscourse,butnowconsiderwritingtheequivalentequationsin polarcoordinates(ρ,ϕ).Wefindthattheyare not:
ρ = mρ
ϕ = mϕ. Wrong! (0.5)
Inotherwords,onedoesnotsimplyreplace x → ρ or y → ϕ andexpecttogetthe rightanswer.(Infact,itisclearthatthesecondequationin(0.5)doesnotevenhave thecorrectunits.)Thecorrectrelationshipsareactually
Thetwosetsofeqns(0.4)and(0.6)arenotidenticalinform,as(0.4)iswiththe (wrong)eqns(0.5).Specifically,thereare“extra”termsandmultiplicativefactorsin (0.6),anditisnotimmediatelyobviouswherethesecamefromorwhetherthereisa patternthatiscommontothem.Itis,however,truethatapplyingeitheroneofthese choicestothesameproblemwilldescribethesamephysicalbehaviorandgivethesame physicalresults.Butwheredidtheextraquantitiescomefrom?Mathematically,they arisefromtherelationshipsthatrelatepolarcoordinatestoCartesiancoordinates,i.e. x = ρ cos ϕ and y = ρ sin ϕ,ascanbeeasilyderivedfromFig.[1.3b].Alloneneeds todoistousecalculustofindhow˙x and˙ ρ (forexample)arerelated,andsoon.In principleoneneedstorederivetheNewtonianequationsofmotioneachandeverytime onemakesaspecificchoiceofacoordinatesystem.Thisisindeedthewayitisusually doneinphysicsclasses.However,whatifthecoordinatesystemis not definedahead oftime?Whatifitdependsonthecurvatureofspaceandtimethatisnot apriori known?Whatifthecoordinatesystem itself arisesasthesolutionoftheproblem understudy?Canonerewrite(0.1)oranyotherlawofphysicsinsuchawaythatit remainscoordinateinvariantandgivesthecorrectsetofequationsfor any coordinate system,whetheritwasknownfromthestartorstilltobederived?Thisistheproblem ofcoordinateinvarianceinphysics,orcovarianceasitismorecommonlyreferredto.
x Preface
Learninghowtodoallofthisisausefulthing,whetheroneisgoingtostudyrelativityornot,becauseitprovidesthestudentwitharecipefordealingwithanychoice ofcoordinatesysteminanyphysicsproblem,whethersuchachoiceisoneofthemore commonones,likepolarcoordinatesintwodimensionsorcylindricalandspherical coordinatesinthree,orlesscommon,suchasparaboliccoordinatesorellipticcoordinates.Inshort,itprovidesthephysicist(orengineer)withapowerfulmathematical toolapplicabletoavarietyofsituations.Italsoactsasaneasy(-ish)introductionto thesubjectof tensor mathematics,rarelydiscussedinanundergraduatesetting,yet encounteredinalmosteverybranchofphysics.Whilethese“tensors”areparticularly usefulinarelativisticsetting,theycanalsobefoundinnon-relativisticmechanicsand inelectrodynamics,andknowledgeoftheirpropertiesandruleswouldbeparticularly usefulforthestudentwishingtodelvedeeperintothesetopics,oratleasthopesfor abetterunderstandingthanisnormallydeliveredtoundergraduates.11 Wewilltouch uponallofthis,andbythetimewearedonewewillhaveageneralunderstandingof (almost)alloffundamental(non-quantum)physicsinacovariantsettingandarbitrary spacetimebackgrounds.Weconcludethebookwiththreechaptersfocusingontopics rarely,ifever,foundinsimilartreatments.Theseare:classicalfields,differentialforms, andmodifiedtheoriesofgravity.Thesechaptersareparticularlygearedtowardsthe studentsinterestedinreadingmodernresearchpapers.Theyshouldprovidejustabit ofextrapreparationaswellaspossiblywhetthereader’sappetiteformore.
Anotetoinstructors:
Thisbookiswrittenfromaminimalist’sperspective.BynostretchoftheimaginationamIclaimingthatthediscussionshereareexhaustiveorcomplete.Infact,I imaginethatmostmathematicianswouldbeparticularlyappalledbythelackofrigor throughout,andmostphysicistswillpointoutthatmanyinterestingapplicationsand discussionscommonlyfoundinsimilarmonographsaremissing.Thisisallquiteintentional.Theintendedaudienceofthisbookarethoseundergraduatestudentswho mayhaveonlyhadintroductorymechanicsandelectromagnetismatthelevelofSerway[1],forinstance,aswellaselementarycalculusuptoandincludingmultivariable calculus.Whilethemathematicalbackgroundgetsabitmoreintenseinsomeplaces, itismyhopethatstudentswithonlythatmuchpreparationcanmanagethemajorityofthebook.Asthestudentsprogressintheirstudiesandreachmoreadvanced coursesinmechanicsandelectrodynamics,onehopesthatthisbook,orthememory thereof,wouldprovideabackgroundtyingallthevariousdisciplinestogetherinone continuousthread.Thethemeofcovariancepermeatesallofphysics,andyetisrarely discussedinanundergraduatesetting.Ihavetriedtomakethebookasself-contained aspossible,suchthatastudentreadingitontheirownwouldmanagemostofitwith aslittlehelpaspossible.
11IttrulyhurtswheninteachinganundergraduateclassIfindmyselfforcedtosaysomethinglike “Thisiscalledtheso-and-sotensor,butunfortunatelywehavenotimeinthisclasstoexplainwhat that really means.”
Preface xi
Onealsohopesthatthisbookcanprovidetheminimummathematicaltraining neededbyundergraduatestudentswishingtodoresearchincertainareasoftheoreticalphysics.Infact,theideaofthebook,aswellasthelevelofdetailandsequence oftopics,hasarisenfrommyyearsofsupervisingundergraduateresearch.Withgraduationdatespreset,onewouldlikeone’sstudentstostarttheirresearchexperience asearlyaspossibleintheircollegeyears,andgettofinishwithinthetimetheyhave available.InmyundergraduatetheoreticalphysicsresearchprogramIhaveusually designedmystudents’learningexperienceinsuchawaythattheywouldbeableto gettotheresearchpartasfastaspossible,amassingtheneededmathematicaltrainingintheshortestpossibleperiodoftime.Inmanycases,Ihaveinstructedthemto focusoncertaintopicswhileskippingothers,becauseofmypreconceivedknowledge ofthenatureoftheresearchproblemthatIwilleventuallyposetothem.Forexample,astudentwhoseresearchwillbecalculatinggeodesicorbitsofcertainspacetime backgroundsneednotwastetheirinitialstudysessionsonunderstandingthedetailsof howthesespacetimeswerederivedinthefirstplace;ratheracursoryknowledgewould beacceptable.Ifundergraduateresearchistheinstructor’sintentioninassigningthis booktotheirstudents,thenitisadvisabletoplantheirreadingaheadoftime.Of course,astheyworkontheirprojectstheymaygobackandstudyinmoredetail thosesectionsthattheyhaveinitiallyonlyskimmedover.Ihavetriedtomakethis bookexhaustiveenoughforthesepurposes,althoughdependingonwhattheresearch mentorhasinmind,otherbooksand/ornotescanbesupplemented.
Ontheexercisesinthebook:
Ihavetriedtoincludeasmanyexercisesforpracticeand/orhomeworkassignmentsas Icouldwithoutoverwhelmingthereader.Manyoftheexercisesinthebookarechosen notonlybecausetheyprovidepracticeonthetopicswediscuss,butalsobecausethey includesomeadditionalmaterialoftheirown.Forexample,someoftheexercises requirethereadertoteachthemselvescomputationaltechniquesnotdiscussedinthe textorreadonatopicthatwedidn’tincludeindetail.Somemayevenbelongenough tocountasafinalprojectorsomethingsimilar,e.g.Exercise 6.49,orExercises 7.26 and 7.27 combined.Theseincreaseinfrequency,aswellasintensity,aswegettothe finalchapters.Awordofwarning,however:Pleasebeawarethatsomeoftheexercises list many differentwaysofpractice;somany,infact,thatthestudentneednotdo all.Forexample,anexercisemaysay“dosuchandsuchforthefollowingcases”and list 10 differentcases;e.g.Exercise 2.22 whichinturnisreferredtomultipletimesin subsequentexercises.Thestudentreallyneed not doallofthelistedcases;onlyenough tofeeltheyhavereachedacertaindegreeofcomfortwiththetechniques.Likewise,if thisbookisusedinaformalcourse,theinstructorshouldchoosesomeofthecases forhomeworkassignments,orevenintroducetheirown.Manyexercisesdependon previousones,however.Forexample,Exercise 2.23 needstheresultsofExercise 2.22, soifthereaderchoosestodo,saythree,ofthecasesin 2.22,thentheywouldonlybe abletodothesamethreecasesin 2.23,andsoon.
xii Preface
Someoftheexercisesassignedalreadyhavesolutionsavailableinvariousplaces aroundtheinternet.Thisisunavoidable.However,itisunderstoodthatitisinyour bestinteresttoworkouttheexercisesyourself, then checkagainsttheavailablesolutions.Itisalsotruethattherearefreelyavailablesoftwarepackagesthatwouldsolve manyoftheexercisesinthisbookforyou.Thisisthecaseformostmathematical topicsinthisdayandage.Iactually encourage thereadertofindanddownloadthese packages,orbetteryetlearntodesignandwriteyourown.Youcandosofromscratch usinganyprogramminglanguageorfromwithinoneofthecommerciallyavailable symbolicmanipulationsoftwarepackages.Inotherwords,youshouldtreatthedigital computerasatoolforlearning, not asawayofavoidingwork.Thechoiceofwhich exercisestodobyhandandwhichtodousingthecomputerismostlylefttothereader ortheirinstructors,evenifnotspecificallystated.Forexample,oncetheinstructoris satisfiedthatthestudentsareabletocalculateaspecificquantitythatusuallytakes hourstofindbyhand,saythecomponentsofaparticularlylargetensor,thenthey mightjustallowthestudentstousesoftwarepackagesfortheremainderofthecourse.
Acknowledgements
Itisverydifficult,ifnotdownrightimpossible,togivecredittoeverysingleperson thatIwouldliketo.ForIbelievethatanydirecthelpIhavehadinwritingthisbookis nomoreimportantthantheindirectpositiveeffectmanypeoplehavehadonmylifein general;withoutwhichIwouldnothavebecomethepersonwhoisabletowritesuch abookinthefirstplace.Assuch,IbegforgivenesstoanyonethatIwon’tmention andassurethemthatIappreciatethemnoless.Tobegin,Imustacknowledgemy parents’love,encouragement,andsupport.Thesearethefoundationsuponwhichwe allgrowandadvance.Restinpeacemomanddad;Ihopeyouareasproudofmeas Iamproudtobeyourson.Secondly,IacknowledgethesupportIhavereceivedfrom myfamilyandclosefriends;youaretoomanytomention,butyouwereallsupportive andunderstandingofmyeffortsinwritingthisbook.Iprobablywouldhaveendedup nowherewithoutyou.ThirdlyImustacknowledgemystudentsoveratleastthepast fifteenyears,inboththeUnitedStatesandEgypt.Ihaveusedthenotesonwhich thisbookisbasedtoteachthemthematerial,andtheyhavealwayshonoredmewith valuablefeedbackandcomments.Iwouldalsoliketothankthecolleagues,teachers, andfriendswhohavehadanimmediateimpactonthisbook,whetherviadiscussions wehavehad,supportandencouragement(sometimessuchalongtimeago),ordirect feedback.Theseare,innoparticularorder:
• Dr.MarkPetersonofMt.HolyokeCollege,MA:Youallowedmetooffermyvery firstclassonthegeneraltheoryofrelativity.ThenotesIdevelopedforthatcourse weretheearliestversionofthisbook.Ourdiscussionsaboutteachingmethods havehadalastingeffectonmeasateacherandasanauthor.Yourencouragement andfaithinmyabilitieshavestayedwithmesincethen.
• Dr.AhmedAlaaEldinAbouelsaoodofCairoUniversity,Egypt:Nowwherewould Ihaveendedwithoutyouradviceandencouragement?Youtookachanceona youngmanwhocametoyouwithnothingotherthanapassionforphysics,and yourgamblepaidoff(Ihope).Notonlydidyouallowmetoabsorbfromyouas muchknowledgeasIpossiblycouldhaveatthetime,youwerealsotheonewho providedtheinitialguidancewhich,quiteliterally,startedtherestofmylife.
• Dr.DavidKastoroftheUniversityofMassachusettsatAmherst,MA:Asmy PhDadvisoryoudidmuchmorethansuperviseme.Youallowedmetopickyour brainsinmanytopicsintheoreticalphysicsandpatientlylistenedtomeasI describedhowIunderstoodthings,evenifmyideassoundedsimpleormundane. Thesethoughts,whichyouencouraged,haveslowlydevelopedandmatured,and becamemajorcontributionstothiswork.Morerecently,thanksfortakingthe timetoreadthemanuscriptandcomingupwithusefulcommentsaswellas suggestionsfornewsections.Iamparticularlygratefultoyouforsuggestingthe subtitleofthebook.
• Dr.EricEdlundoftheStateUniversityofNewYorkCollegeatCortland,NY: Thanksforthetimeyoudedicatedtoreadingthemanuscriptandprovidingexcellentsuggestionsandcomments.
xiv Acknowledgements
• Mr.TariqSaeedoftheUniversityofMansoura,Egypt:Thanksforproviding valuableinputfromastudentperspective.Yoursuggestionsonsections §3.3, §4.7,andotherswereparticularlyuseful.Ialsotrulyappreciatedyourtakingthe timetocheckmanyofthecalculationsinthisbook.
• EngMuhammadEl-Nashash’ee,andEngAkramMasoud:Thankyoufortaking thetimetoreadthemanuscriptandprovidingvaluablefeedbackandsuggestions.
• MycousinanddearfriendBrigadierGeneralEngOmarFarouk:Manythanksfor thebigpushyougavemeatatimeIdesperatelyneededone.
• Last,butcertainlynotleast,mydearfriendMr.AhmedAbuali:Iwillalwaysbe gratefulforyourvaluableinput,help,aswellasmanyhoursofdiscussion.
5GeneralCovariance
5.1WhatisSpacetimeCurvature?
5.3TheNewtonianLimit:TheMetricofWeakGravity
5.4TheMetricOutsideaSphericalMass
5.5TheMetricInsideaSphericalMass
5.6AreasandVolumesinCurvedSpaces
5.7Non-RotatingBlackHoles
5.8CosmologicalSpacetimes
6PhysicsinCurvedSpacetime
6.1GenerallyCovariantMechanics
7.2CalculusonManifolds
7.4TheVacuumEinsteinEquations
7.5TheStressEnergyMomentumTensor
7.6TheEinsteinFieldEquations
7.7Einstein’sGreatestBlunder
8.1ThePrincipleofLeastAction
8.2ClassicalFieldTheory
8.3TheStressTensorfromtheAction
8.4GeneralRelativisticActions
8.5TheGeodesicEquationOneMoreTime
8.6SomeMoreSpacetimes
9.1AnEasy-GoingIntro
9.2MoreGenerally...
9.3HodgeDuality
9.4Maxwell’sTheoryandDifferentialForms
9.5Stokes’Theorem
9.6Cartan’sFormalism
f (R)Theory
WiththeexceptionofFig.[5.12]and[8.7],allthefiguresareoriginalbytheauthor.
Softwareused:“WolframMathematica R 11.3,”and“Inkscape R 0.92.”
CoordinateSystemsandVectors
Geometryhastwogreattreasures:oneistheTheoremofPythagoras;theother,thedivision ofalineintoextremeandmeanratio.Thefirstwemaycomparetoameasureofgold;the secondwemaynameapreciousjewel.
JohannesKepler
Introduction
Coordinatecovarianceisdefinedastheinvarianceofthelawsofphysicsunderchange ofcoordinatesystems,whethertheydifferfromeachotherbytranslation,rotation,or both.Inthischapterwebeginbyintroducingthevarioustwo-andthree-dimensional coordinatesystemsusuallyusedinproblemsofphysicsandengineering.Someofthese shouldbequitefamiliartothereader,whileothersmaybecompletelynew.Wespecificallyhighlighttheconceptof“lineelement,”alsoknownasthe“metric,”asadefining principleofcoordinatesystemsaswellasaunifyingthemeamongstthem.Thisshould allowforasmoothertransitionintophysicslater.Inprinciple,allthatanexperienced physicistneedsinordertofigureoutwhattypeofcovarianceisatplayinagiven situationisknowledgeofthemetric.Henceintroducingtheconceptearlyonmakes senseandallowsustimetogetusedtoitbeforethingsgetmoreinteresting.Next wewillturntodefiningthebasicsofvectormathematicsanddiscussingtheirformulationinanewlanguagesimplyknownasthe“index”or“component”notation.1 Thisnotationbyitselfconnectsvectorstothecoordinatesystemstheyaredefinedin andhighlightstheircovariance.Furthermore,thenotationprovidesthemajorityof themathematicalmaterialthatweneedtocollectinoursearchforafullycovariant formulationofphysics,relativisticornot.Infact,Iclaimthatthefirsttwochapters bythemselves constituteatleast80percentofthemathematicsneededtostudy both theoriesofrelativity.Asthereaderwillsee,noneofthismathematicsistoofarbeyond ordinaryalgebraandabitofmultivariablecalculus.
1Alsosometimesreferredtoasthe“tensornotation;”however,thisissomewhatmisleading,sowe willavoidusingittoomuch.
1.1CoordinateSystems
Forthepurposesofmanyscienceandengineeringapplications,themostcommonly usedsystemofcoordinatesisthe Cartesian, 2 alsoknownas box or rectangular coordinates.Bytheirverynature,Cartesiancoordinatesemphasizetheintuitiveconceptsofwidth,depth,andheight.Itisusuallythecoordinatesystemofchoicefor Euclidean geometry;i.e.theordinarygeometryweallstudiedinschool.Itis,however,only one choiceamongmany,aswewillsee.Euclideangeometrydescribesflat space,whereparallellinesstayparallelandtheanglesofatrianglesumuptoexactly 180◦.Ifonehappenstobeinterestedincurvedor non-Euclidean geometries,like cartographersdoinggeometryonthesurfaceofthesphericalglobe,thennotonlydo Cartesiancoordinatesstopmakingsense,buttheyactuallybecomeimpossibletodefine,exceptapproximatelyonaverysmallscale.Toclarifythis,considerthesurfaceof planetEarthasanexample,assumedaperfectsphere;onecandrawstraightlinesin agridonthefloorinaroomorinthestreetwithouttrouble,butifyouwanttodraw longer“straight”linesbetweencities,countries,orevencontinents,youfindthatyou cannotdosoandareforcedtoworkwithcircles,likethoseoflatitudeorlongitude.In asense,then,mostcurvedsurfacesofinterestareapproximatelyflatonsmallscales; onesaystheyare locally flat,asopposedto globally so.
(a)Aright-handedcoordinatesystem. (b)Aleft-handedcoordinatesystem.
Fig.1.1:Cartesiancoordinates.
Traditionally,weusethesymbols x, y,and z todenotethethreeCartesianaxes inthree-dimensionalspace,orderedintheso-called“right-handed”system,asshown inFig.[1.1a].Theright-handednessconventionisparticularlyusefulinphysics,as itisthebasisofvariousmathematicaloperationssuchasvectorcrossproducts.For comparisonaleft-handedsystemisshown,butwewillnotbeusingthat.Generally,
2InventedintheseventeenthcenturybytheFrenchphilosopherandmathematicianRen´eDescartes (1596-1650),whosenameinLatinizedformisCartesius.
CoordinateSystems 3
coordinatesystemsaredefinedviathegeometricshapestheyseemtotrace.Soin thecaseofCartesiancoordinates,surfacesofconstant x, y,and z areinfiniteflat planesasshowninFig.[1.2],hencethealternativetitle“boxcoordinates.”Nowthe conventionalchoiceoftheletters x, y,and z todenotetheCartesianaxesisvery familiartomostpeople;however,amoreusefulnotation,andonethatwemightas wellstartusingrightaway,employs indices todenotethedifferentaxes.So x becomes x1 (i.e.the first axis), y,beingthesecondaxis,becomes x2,and z → x3,where thereaderiswarned not toconfuseindiceswithpowers,so x2 isnot x squared, butissimplypronounced“extwo”andsimilarlyfor“exone”and“exthree.”Ifwe wishtodenoteexponentiation,thenwecansimplyuseparentheses;forexample,the squareof“exthree”is x3 2 = x3 × x3 = z2.Ifthereisapossibilityofconfusion, wecantemporarilygobacktotheold(x,y,z)system,dependingonthecontext. This“numbering”system,alsoknownasthe indexnotation orthe component notation,isamuchmorepowerfulchoicethantheconventionaloneforavarietyof reasons,aswewillsee.

Fig.1.2:TheCartesiangrid:planesofconstant x, y,and z.
Thenextmostcommonlyusedsystemofcoordinatesinthreedimensionsis cylindricalcoordinates (whichbecome polarcoordinates inthe x–y plane),alsoknown as cylindricalpolarcoordinates.Theyaredenotedby(ρ,ϕ,z)andarerelatedto theCartesiancoordinatesvia
CoordinateSystemsandVectors
andtheirinverse
asiseasytoconfirmbyinspectingFig.[1.3].Cylindricalcoordinatesareaparticularly usefulchoiceinphysicswhentheproblemunderstudyhascylindricalsymmetry,i.e. studiesasituationwithcylindricalshapesorareasonableapproximationthereof. Thenamecomesfromthefactthatsurfacesofconstant ρ describeinfinitecylinders spanningtheentire z direction.Surfacesofconstant z areofcoursestillinfiniteplanes, andsoaresurfacesofconstant ϕ (Fig.[1.4]).
(a)Cylindricalpolarcoordinates. (b)Planarpolarcoordinates.
Fig.1.3:Two-andthree-dimensionalcylindricalpolarcoordinates.
Animportantdifferencebetweenthecylindrical(aswellastwo-dimensionalpolar) andCartesiancoordinatesystemsisthatthecylindricalsystemdoes not coverallof three-dimensionalspace.Whatthismeansisthatwhileanypointinspacecanbe describedbyaspecificsetofnumbersinCartesiancoordinates x1,x2,x3 ,inthe cylindricalcoordinatesystemthereisasinglepoint,outoftheinfinityofpointsin space,that cannot bedescribedbyauniquesetofthethreenumbers(ρ,ϕ,z).This isthepointlocatedexactlyattheoriginofcoordinates,whichweusuallydenoteby O.Whilethecoordinatesof O intheCartesiansystemaresimply(0, 0, 0),inthe cylindricalsystemonly ρ =0and z =0canbedefinedbut ϕ remainsambiguous, because any valuecanbeusedforit.Inotherwords,thereisnouniquesetofthree
CoordinateSystems 5
numbersdescribingthelocationof O;thesetofnumbers(ρ =0,ϕ =0◦,z =0)does implytheorigin,butsodothesets(ρ =0,ϕ =10◦,z =0),(ρ =0,ϕ =20◦,z =0), (ρ =0,ϕ =312 56◦,z =0),andsoon.Thereisaninfinitenumberofpossibilities,all describingasinglepoint!Thisphenomenonisa defect inthecoordinatesystemitself andcannotberemedied;thesystemsimplyfailsatthatspecificpoint.Onethensays thatwhileCartesiancoordinates cover, map,or chart allthree-dimensionalspace, cylindricalpolarcoordinatesdonot;exactlyonepointdefiesdefinition.Coordinate systemsinthisregardcanbethoughtofasagridcoveringthree-dimensionalspace; theCartesiangridormapisinfinite,smooth,andcomplete,whilethepolaronehas a“hole”initlocatedat O.Ifonethenwishestodoaproblemthatstudiesthepoint attheoriginusingsucha“defective”coordinatesystem,onehasnochoicebutto shiftthecoordinatesystemitselfsuchthatthepointinquestionnolongercoincides withtheorigin.Thereissimplynootherway.Thisissuealsofurtheremphasizesthat spatialpointsandcoordinatemapsare not thesamething;anobviousissue,perhaps, butonethatissometimesconfusedinthemindsofbeginners.
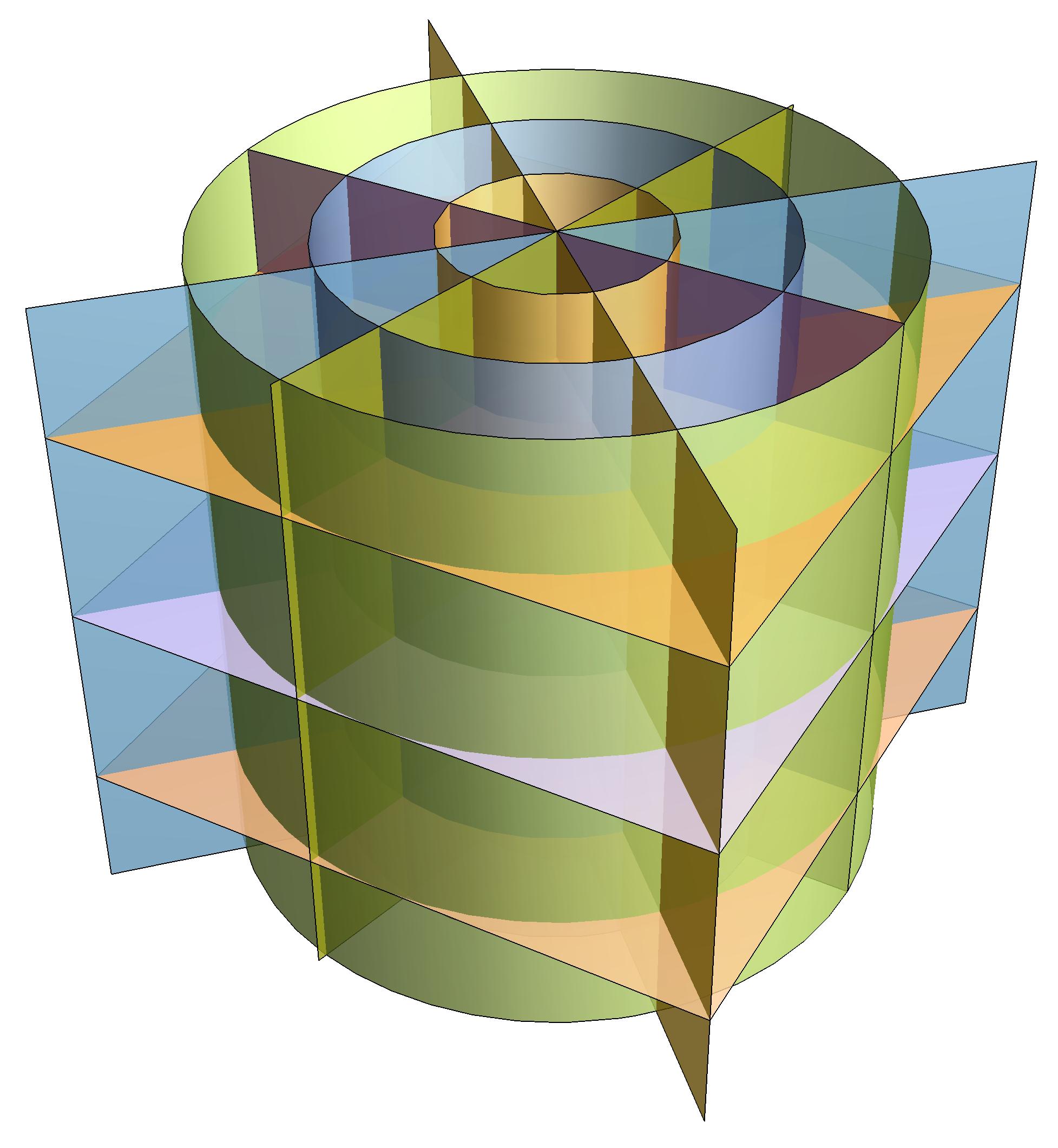
Fig.1.4:Thecylindricalcoordinatesgrid:cylindersofconstant ρ andplanesofconstant z and ϕ
Theremainingmostcommonlyusedsystemofcoordinatesinthree-dimensional spaceisthe sphericalcoordinatesystem,particularlyusefulinphysicswhenproblemsexhibitsphericalsymmetry.AsshowninFig.[1.5],wedefinethenumbers(r,θ,ϕ). TheyarerelatedtotheCartesiancoordinatesasfollows:
CoordinateSystemsandVectors
Fig.1.5:Sphericalcoordinates.
Itisalsopossibletodefinetransformationrelationsbetweencylindricalcoordinates andsphericalcoordinates.Theseare:
Notethatthesphericalcoordinatesystemalsosuffersfromthesamedefectwe notedforcylindricalcoordinates.Onceagain,thepointattheorigincannotbespecified bythreeuniquenumbers:only r =0canbeused,while both θ and ϕ areambiguous. Asbefore,theonlywaytodealwiththisincalculationsistoavoidaddressingthe originaltogetherorjustshiftthecoordinatesystem.Nowthedefiningpropertyof sphericalcoordinatesisthatsurfacesofconstant r describespheres,concentricatthe origin,whilesurfacesofconstant θ and ϕ defineconesandflatsurfacesrespectively, asshowninFig[1.6].
Asnoted,coordinatesystemsaredefinedbasedongeometricshapes:flatplanes forCartesian,cylindersforcylindrical(orcirclesforpolar),andspheresforspherical. Wenoteherethattheseare not theonlyoptions;othershapescanalsobeusedto
CoordinateSystems 7
(a)Spheresofconstant r andconesofconstant θ insphericalcoordinates.
(b)Thecompletesphericalcoordinatesgrid.
Fig.1.6:Sphericalcoordinates.
definecoordinatesystems.Forexample,considertheso-called ellipticcylindrical coordinates (u,v,z),wheresurfacesofconstant u defineconcentricellipticcylinders andsurfacesofconstant v arehyperbolas,asshowninFig.[1.7].Theyarerelatedto theCartesiancoordinatesvia
x 1 = a cosh u cos v
x 2 = a sinh u sin v
x 3 = z, (1.6) where a isanarbitraryconstant.
Therearecoordinatesystemsbasedontheparabolicshape,suchas parabolic cylindricalcoordinates,asshowninFig.[1.8]:
Afinalexampleisthe paraboliccoordinates,asshowninFig.[1.9]:
x 1 = uv cos θ
x 2 = uv sin θ x 3 = 1 2 u 2 v 2 (1.8)
















