Conceptsofmaterialsscience
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries
c AdrianP.Sutton2021
Themoralrightsoftheauthorhavebeenasserted
FirstEditionpublishedin2021
Impression:2
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica
BritishLibraryCataloguinginPublicationData
Dataavailable
LibraryofCongressControlNumber:2021934825
ISBN978–0–19–284683–9(hbk.) ISBN978–0–19–284644–0(pbk.)
DOI:10.1093/oso/9780192846839.001.0001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY.
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
InmemoryofmyparentsPeterandBerylSutton
Abouttheauthor
EducatedinmaterialsscienceattheUniversitiesofOxfordandPennsylvania,Adrian SuttonhasheldprofessorshipsatOxfordUniversity,AaltoUniversityandImperial CollegeLondon.Amaterialsphysicist,addressingfundamentalaspectsofthescience ofmaterials,hehastaughtacrosstheundergraduatecurriculum.Hehasconsultedfor companiesintheUnitedStates,JapanandtheUK.HewaselectedtoaFellowshipof theRoyalSocietyin2003.HeisafounderoftheThomasYoungCentre,theLondon CentreforTheoryandSimulationofMaterials.Hewasalsothefoundingdirectorin 2009oftheCentreforDoctoralTraining(CDT)onTheoryandSimulationofMaterialsatImperialCollege,whichattractedintomaterialssciencemorethanahundred graduatesfromtheUKandoverseaswithfirstclasshonoursdegreesorequivalent inphysicsandengineering.Hisbook RethinkingthePhD istheextraordinarystory ofthisacclaimedCDT.In2012hewasawardedtheRector’sMedalforOutstanding InnovationinTeachingatImperialCollege.In2018heleftpaidemploymenttofocus onscholarship,andImperialCollegeconferredthetitleofprofessoremeritusonhim. HelivesinOxfordwithhiswifePatWhite.
Preface
Alltechnologiesdependontheavailabilityofsuitablematerials.Withoutinnovations inmaterialswewouldstillbelivingincaves.Theepochsofcivilisationhavebeen definedbythematerialspeoplehaveused,fromthestoneagetothebronzeageto theironageandnowthesiliconage.MarkMiodownikhaswritteneloquentlyabout howcountlessmaterialsshapeourlives1.RobertCahnwroteanauthoritativehistory oftheemergenceofmaterialsscience2 .
Thisbookisdifferent.Itisanattempttoidentifykeyconcepts–bigideas–ofthescienceofmaterials.Itisnotaboutanyparticularexperimental,theoretical orcomputationaltechniqueoranyparticularmaterials.ItdescribestenconceptsI believearecentraltomaterialsscience.
OnedifficultyIfacedinwritingthisbookwastheoverlapbetweenmaterialsscience andcondensedmatterphysics,solidstatechemistry,mechanicsofsolidsandbiology. MaterialssciencehasbecomesobroadthatforalongtimeIwonderedwhetherthere areanyconceptsthattiethesubjecttogether.
Ithinkofmaterialsasasubsetofcondensedmatter,distinguishedbyhavingause inanexistingorintendedtechnology.Thelinktotechnologyisthe raisond’ˆetre ofthe subject.Itexplainswhythestudyofmaterialsinvolvesscientistsandengineers,and whyitisoftendescribedasan‘enablingdiscipline’becauseitfacilitatesadvancesin technology.Ihavetriedinthisbooktohighlightthefundamentalnatureofmaterials scienceandtheinexhaustiblerichnessofitsintellectualcontent.
Theengineeringofmaterialsmaybedescribed3 asthe exploitation oftherelationshipsbetweenthestructure,propertiesandmethodoffabricationofamaterial,to designamaterialwithoptimumperformanceforparticularapplications.Thescience ofmaterialsmaybedescribedas understanding thoserelationships.Understanding andexploitingthoserelationshipstodesignandcreatematerialsforapplicationsin technologyistheessenceof‘Materials’asadiscipline.
ToidentifycoreconceptsofmaterialsscienceIhadtopeelawaylayersofdetail inthesearchforideasthatpervadethesubject.Inevitablysomeoftheconceptsare commontomainstreamphysicalsciences,suchasthermodynamicstability(Chapters 1 and 2),symmetry(Chapter 5)andquantumbehaviour(Chapter 6).Inthosecases Ihavefocusedontheirparticularsignificanceinmaterialsscience.
Thermodynamicsdefinesthestablestateofamaterialinitsenvironment.Itis rareforamaterialtobeinthisstablestate,butitisthestatetowardswhichthe
1Miodownik,M, StuffMatters,PenguinGroup(2013).
2Cahn,RW, TheComingofMaterialsScience,Elsevier(2001)
3NationalResearchCouncil1989. MaterialsScienceandEngineeringforthe1990s:Maintaining CompetitivenessintheAgeofMaterials,Chapter1:Whatismaterialsscienceandengineering? p.19-34.NationalAcademiesPress:WashingtonDC. https://doi.org/10.17226/758
materialwillevolveifitisleftaloneinitsenvironment.Thisimmediatelyintroduces theideaofchangeinamaterial,eithertowardsathermodynamicallystablestateor someotherstatedeterminedbyitsexposuretoforcesofvariouskinds.Incrystalline materialsdefectsofvariouskindsaretheagentsofchange(Chapter 4).Therateof changeisdeterminedbyrestlessatomicmotioninmaterials,bothinfacilitatingthe motionofdefectsandinretardingthem(Chapter 3).Defectsandtheirinteractions incrystallinematerialsareaperfectillustrationoftheconceptofemergenceofnew physicsinmaterialsatlargerlengthscalesthroughcollectivebehaviouratsmaller lengthscales(Chapter 8).Theemergenceofnewphysicsacrosstherangeoflength scalesfromelectronstoengineeringcomponentsisadefininganduniquefeatureof materialsscience.Theabilitytomanipulatethestructureofmaterialsacrossthisrange oflengthscalestoachievedesiredpropertiesleadstotheconceptofmaterialsdesign forparticularapplications(Chapter 9).
Sizemattersinmaterialsbecausetheirpropertiesaremoreobviouslydominatedby quantumphysicsatthenanoscale(Chapter 7).Thishasledtotheriseofnanoscience andnanotechnologywhichhaveunderpinnedthemodernageofinformationstorageandprocessing.Untilmetamaterialswereintroducedaroundtheturnofthe21st centurytherewerenomaterialsthatdisplayedcertainproperties,suchasnegative refraction.Metamaterialsremovedthislimitationbecausetheirpropertiesarenotdeterminedbytheirchemistrybutbytheircarefullydesignedstructure(Chapter 10). Treatingbiologicalmatterasamaterialhasledtotheconceptofactivematterinwhich complexityandself-organisationarisefromthecollectiveactionofenergy-consuming agents(Chapter 11).
Ihavestrivedtomakethisbookintelligibleforanyonewithapre-universityeducationinphysics,chemistryandmathematics.OnthewholeIhavelimitedtheuseof mathematicstoelementaryalgebraandquotingtheoccasionalusefulformula.Only inChapter 10 haveIrelaxedalittlethisself-imposeddiscipline.Suchashortbookas thiscannotbeself-contained.Therearereferencestobooksinthefurtherreadingat theendofeachchapter.Referencestoresearchpaperswithhyperlinksintheelectronic versionareincludedinfootnotesforthereaderwhowantstodelvedeeper.
Undergraduatesandmastersstudentsofmaterialssciencemayfindthisbooka refreshingandenlighteningsupplementtotheirusualreading.Graduatesinother subjectsmaygainanimpressionofwhatmaterialsscienceisabout,andIhopeitwill drawthemintopostgraduatestudyofthesubject.Ihopemycolleaguesinmaterials sciencewillfinditstimulatingandoccasionallyprovocative.
Thisis not atext-book.Muchofwhatisintext-booksonmaterialsscienceisnot treatedinthisbookand viceversa.Nevertheless,thisbookdoescoveralotofground.
IamgratefultoBobBalluffi,CraigCarter,MartinCastell,PeterDobson,Mike Finnis,PeterHaynes,PeterHirsch,StanLynch,TonyPaxton,JohnPendry,BobPond, LucaReali,ChrisRace,TchavdarTodorov,VasekVitekandanonymousreviewersfor helpfulcomments.Anyremainingerrorsaremyresponsibility.
Finally,IthankPatforhersupport,encouragementandeditorialskill.
ImperialCollegeLondon December2020.
6.4Identicalparticles,thePauliexclusionprincipleandspin
Whenisamaterialstable?
Atheoryisthemoreimpressivethegreaterthesimplicityofits premises,themoredifferentthekindsofthingsitrelates,andthe moreextendeditsareaofapplicability.Hencethedeepimpressionthat classicalthermodynamicsmadeuponme.Itistheonlyphysicaltheory ofuniversalcontentconcerningwhichIamconvincedthat,within theframeworkofapplicabilityofitsbasicconcepts,itwillneverbe overthrown.
AlbertEinstein,AutobiographicalNotesp.31,translatedandeditedby PaulArthurSchilpp,OpenCourtPublishingCompany(1996).ISBN 0812691792. c TheHebrewUniversityofJerusalem.Withpermission oftheAlbertEinsteinArchivesandofCricketMedia.
1.1Concept
Whentheyarenotbeingdeformed,irradiated,orconstantlydisturbedbyothermeans, materialsevolvetowardsastateofequilibriumwiththeirenvironments.Thermodynamicsdefinestheconditionsforsuchequilibriumundervariousenvironmentalconditions.Phasediagrams1 aremapsoftheequilibriumstatesofamaterialasthetemperatureandconcentrationsofitsconstituentsarevaried,usuallyatatmosphericpressure.
1.2Introduction
Mostmaterialsareunstableormetastable.Amaterialisinametastablestateif itsenergyisatalocalminimum,butnotthelowestenergystate.Acorrielakeisa metastablelocationofwater.Waterinthelakeattainsitslowestenergywhenitreaches thesea.Ifitistoreachtheseawithoutevaporatingthewaterlevelinthelakehastorise abovethelipretainingit.Whenmaterialsareundisturbedtheyevolvetowardsastable stateinwhateverenvironmenttheyarein.Theevolutionmayinvolveobviouschanges takingplacesuchascorrosion,wherethesurfaceofthematerialreactschemicallywith gasesorliquidsintheenvironment.Lessobviousarethechangesthatmaybetaking placeinsidethematerial.Theymayalsobechemicalinnature,involvingthemovement ofatomstowherethechangesaretakingplace.Theremaybeotherchangestothe internalstructureofthematerial,involvingareductionintheconcentrationofdefects, whichIwilldiscussinChapter 4.Dependingonthetemperatureofthematerialand
1Phasediagramsarediscussedinthenextchapter.
Whenisamaterialstable?
theenergybarriersthathavetobeovercome,someoftheseprocessesmaybeoccurring imperceptiblyslowly,insomecasesonageologicaltime-scale(hundredsofmillions ofyears).Othersmaybeoccurringinpicoseconds(10 12 s).Thepossiblerangeof time-scalesfortheseprocessesspans27ordersofmagnitude2
Thereareotheroccasionswhenmaterialsaredrivenawayfromastablestate. Forexamplethezirconiumcladdingofthenuclearfuelrodsinapressurisedwater nuclearreactorisbeingconstantlybombardedbyneutrons.Lowdensitypolythene undergoeschemicalchangeswhenitisexposedtosunlight,becomingbrittleandreleasingmethaneandethane.Railsdeformandoccasionallydevelopcracksthroughthe repeatedloadingduetotrainspassingoverthem.
Thermodynamicsdefinestheconditionsfordifferentregionswithinamaterialto beinequilibriumwitheachotherandwithanyenvironmentthematerialisin.Ifthe materialisabletoexchangeenergyand/ormatterwithitsenvironment,equilibrium involvesthoseexchangesaswell.Whenamaterialisinequilibriumitisstableinthe sensethatitdoesnotundergoanyfurtherchanges.Inthischapterwewillfindout whatthoseconditionsare.
Anyonewhostudiesaphysicalscienceorengineeringwilleventuallymeetthermodynamicsbecauseitsconceptsandprinciplesaresouniversal,asEinsteinremarked inthequoteatthebeginningofthischapter.Wearegoingtogoonquiteajourneyin thischapterandIamnotgoingtoassumeyouknowanythingaboutthermodynamics. Butfirstweneedtodefinecertaintermswewillbeusing.
1.3Definitions
Inthermodynamicstheobjectweareconsideringanditsenvironmentiscalledthe system.Thereare isolatedsystems inwhichanobjectissurroundedbyboundaries thatareimpenetrabletoenergyandmatter.Theobjectisthenseparatedfromits environmentandthesystemcomprisestheobjectonly.Iftheobjectcanexchange energybutnotmatterwithitsenvironmentthesystemiscalled closed.Therearealso opensystems inwhichanobjectcanexchangeenergyandmatterwithitsenvironment. Althoughtheoverallchemicalcompositionofanobjectineitheranisolatedorclosed systemdoesnotchange,therecanbearedistributionofelementswithintheobjectas itevolvestowardsequilibrium.Thestateofequilibriumofanobjectdependsnotonly ontheobjectitselfbutalsoonwhetherandhowitinteractswithitsenvironment.
Thechemicalspeciesthatmakeupthesystemarecalled components.Theymaybe atoms,suchasironandcarbon,ormolecules,suchaswaterandmethane.The chemical composition ofamulti-componentsystemisthespecificationoftheconcentrationof eachcomponentpresent.Inamulti-componentsystemitisquitecommontofind regionsinwhichtheatomicstructureandchemicalcompositionareconstant.Sucha regioniscalleda phase.Iftheregionoccupiedbythephaseisonlynanometresinsize thenasignificantfractionoftheatomswillbeclosetothesurfaceorinterfacebounding it.Thestructureandcompositionofsuchasmallregionmaythendiffersignificantly fromamacroscopicregion.Itisdoubtfulthatsuchasmallregioncanbeclassifiedas
2Anorderofmagnitudeisafactoroften.Twentysevenordersofmagnitudemeansafactorof 1027 .
aphase.Thisisonereasonwhythermodynamicsappliesonlytomacroscopicsystems, containinglargenumbersofparticles.
WeareusedtousingtemperaturescalesliketheCelsiusscale3,thezeroofwhich correspondstothefreezingpointofpurewater,andforwhichnegativetemperatures arepossible.Inthermodynamicsweusean absolute temperaturescale,measuredin kelvin,thezeroofwhichrepresentsanabsoluteminimumtemperature.Onewaythis scalecanbedefinediswiththenotionofan idealgas:acollectionofperfectpoint particleswhichdonotinteractwithoneanotherexceptwhentheycollide.Atafixed pressure,aquantityofanidealgashasavolumethatisproportionaltothetemperaturemeasuredontheabsolutescale,becomingzeroatzerotemperature.Thisabsolute zeroontheKelvinscaleisequalto-273.15degreescelsius.Therefore,thetemperature inkelvinequalsthetemperatureindegreescelsiusplus273.15.
Heat isthe kineticenergy oftherandommovementofatomsthatmakeupan object.Whenhotandcoldbodiesarebroughtintocontactkineticenergyofatomsin thehotbodyistransferredtoatomsinthecoldbodythroughatomiccollisions.We saythattheyhavereachedthesametemperaturewhenthereisnofurthernettransfer ofatomickineticenergybetweenthem.Atamicroscopicleveltherearelocaltransfers ofkineticenergybetweenbothbodiesthroughatomiccollisions,buttheysumtozero onaveragewhenthebodieshavethesametemperature.
Atomsthatmakeuptheobjectofstudyalsohave potentialenergy.Itarisesfrom theattractiveandrepulsiveforcestheyexertoneachother,andfromtheirinteractionwithelectric,magneticandgravitationalfieldsimposedontheobjectbyits environment.Inasolidthepotentialandkineticenergiesofeachatomarechanging continuouslyandextremelyrapidlybecauseeachatomisvibratingaboutitsaverage position.Theperiodofvibrationisaround10 13 seconds.Inacubiccentimetreofa solidtherearearound1022 atoms.Todefinethestateofacubiccentimetreofasolid intermsoftheinstantaneouskineticandpotentialenergiesofeachatomisimpossible. Itisalsounnecessary.Inthermodynamicsthestateofasystemcomprisingasingle componentcanbedefinedintermsofonlytwovariables,called statevariables.For example,thethermodynamicstateofafixedamountofasinglecomponentsubstance isdeterminedbyitsequationofstate,whichrelatesthethreestatevariablespressure, volumeandtemperature.Whenanytwoofthesethreestatevariablesarespecifiedthe thirdisdeterminedbytheequationofstate.Furthermore,unlikethekineticandpotentialenergiesofindividualatomsthesestatevariablesareexperimentallymeasurable. Statevariablesandpropertiesareeitherextensiveorintensive. Extensivevariables are proportionaltothesizeofthesystem,suchasvolume,theamountofacomponent andinternalenergy. Intensivevariables areindependentofthesizeofthesystem,such astemperature,pressureandchemicalpotentials(chemicalpotentialsarediscussedin section 1.9).
Whenamaterialisinequilibriumtheintensivevariablestemperature,pressure andchemicalpotentialsareconstantthroughoutthesystem.Thisisthedefinitionof the equilibriumstateofamaterial intheabsenceofanyfieldsactingonthematerial, suchasgravity.Whensuchfieldsexisttheyhavetobetakenintoaccountinthe determinationoftheequilibriumstate.Forexample,thepressurewithinacolumn
3In1948thecentigradetemperaturescalewasrenamedthecelsiusscale.Theyareidenticalscales.
Whenisamaterialstable?
supportingatallbuildinghastoincreaseaswegodownthecolumntomaintain mechanicalequilibrium.
Aswehavealreadynoteditiscommonforamaterialnottobeinequilibrium. Provideditisnotbeingdrivenawayfromequilibriumthisstateremainsimportant becauseitisthestatetowardswhichthesystemevolves.Inthatcaseitprovidesthe direction ofchangewithinthematerial.Butitdoesnotprovidethe rate ofchange becausetimedoesnotappearinequilibriumthermodynamics.Althoughmanyofthe mostusefulmaterialsarenotatequilibriumtheyareinmetastablestatesthatcan endureformuchlongerthantheservicelifeofthematerial.Thisfeatureofmaterials isexploitedextensivelyintheirdesign,asdiscussedinChapter 9
1.4Thefirstlawofthermodynamics
Thefirstlawofthermodynamicsistheconservationofenergy:
Energycannotbecreatedordestroyed.Itcanonlybeconvertedfromoneformto another.
AsweshallseeinChapter 5 theultimateoriginofthislawisasymmetryofa particularkind.Formsofenergyincludekineticenergy,heatandvariousformsofpotentialenergysuchaschemicalenergy,electricalenergy,magneticenergy,gravitational energy,andsoon.
Energy isthecapacitytodowork4.Inthermodynamics work doesnothavethe usualmeaningoflabour.Ithasthesamemeaningasinmechanics.Workisdonewhen thepointofapplicationofaforcemovesinthedirectionoftheforce.Theworkdoneis equaltotheforcemultipliedbythedisplacementofthepointofitsapplicationinthe directionoftheforce.Whenworkisdoneenergyistransferred.Iftheforceisexerted onanobjectbyitssurroundings,andthepointofitsapplicationisdisplacedinthe directionoftheforce,energyistransferredfromthesurroundingstotheobject,and viceversa.Whenyoustretchaspringbypullingonitsendsyouaredoingworkonthe spring.Theworkyouhavedoneisconvertedintopotentialenergyinthespring.Ifyou releaseoneendofthespringitretractsquicklyanditspotentialenergyisconverted intokineticenergy.Weshallseethatinthermodynamicsthereareotherformsofwork, notonlythoseofamechanicalorigin.
The internalenergy ofanobjectcanincreaseintwowaysinaclosedsystem. Itcanreceiveheatanditcanhaveworkdoneonit.Ifitlosesheatorifitdoes workitsinternalenergydecreases.Inanopensystem,wheretheobjectcanexchange matterandenergywithitsenvironment,itsinternalenergycanalsochangethrough theadditionorremovalofatoms.Ifanatomofaparticularelementisaddedtothe system,withnosimultaneoustransferofheatorwork,theinternalenergyincreases byanamountcalledthe chemicalpotential oftheelement.Chemicalpotentialsare intensivevariablesliketemperatureandpressureandweshallseethattheyplaya centralroleintheequilibriumofisolated,closedandopenmulti-componentsystems.
4Inthenextsectionwewillseethereisalimitationontheconversionofheatintowork.Amore precisestatementisthat free energyisthecapacitytodoworkunderspecifiedconditions.Freeenergy isintroducedinsection 1.7.
Theequilibriumstateofasystemisnotdeterminedbyminimisationoftheinternal energyalone,exceptatextremelylowtemperatures.Forexample,whenasolidmelts itsinternalenergyincreasesbecauseitabsorbslatentheat,butmeltingisachangeof phasetoanewequilibriumstate.Theotheressentialingredientisthe entropy ofthe system.Inclassicalthermodynamicsentropyisdefinedsomewhatabstractlybythe propertiesofheatengines,whichwewillnotgointohere.Inthenextsectionwewill introduceentropyinmorephysicalterms.
1.5Thesecondlawofthermodynamics
1.5.1Irreversibilityandentropyproduction
Amanisfilmedashefallstenmetresintoatall,thermallyinsulatedtankcontaining 100cubicmetresofwater.Thereisasplashashisbodydisplaceswater.Nowater escapesbecausethetankwallsarehigh.Wavesarecreatedandreflectedoffthewalls. Hefinallycomestorestafloat,thewavesdieawayleavingaflatsurfaceofthewater, andallthewatersplashesrundownthesidesofthetankbackintothebodyofwater.
Weknowimmediatelyifthefilmisplayedbackwardsbecauseitshowsanimpossible sequenceofevents.Howcanaman,startingfromastationarypositioninperfectly stillwaterinatank,emergecompletelydryandflythroughtheairatasufficient speedtoreachhisoriginalpositiontenmetresabovethewater?Althoughthisis obviouslyimpossibleitdoesnotviolatethefirstlawofthermodynamics!Thepotential energythemanhadwhenhewastenmetresabovethewaterisconvertedintohis kineticenergyashefallstowardsthewaterandthenintokineticenergyofwater moleculesinthetank.Inotherwords,thewateriswarmer.Accordingtothefirst lawofthermodynamicsthereisnoreasonwhytheheatthathasbeenimpartedto thewatercannotbeconvertedbacktopotentialenergybysendinghimbacktohis originalpositionabovethetank.
Byrunningthefilmbackwardsweareseeingaworldinwhichthedirectionoftime hasbeenreversed.Theequationsgoverningtheman’smotionandthemotionofthe watermoleculesareexactlythesameiftimeisreversed.Theydisplay‘time-reversal symmetry’.Areturntohisoriginalpositionabovethetankdoesnotviolatethese equationsofmotionbecausetheyareindependentofthedirectionoftime.Butallour instinctstellusthisisimpossible.
Whatarewemissing?In100cubicmetresofwatertherearearound1030 molecules. Eachofthesemoleculescanbeanywhereinthe100cubicmetrevolumeofwater.They havearangeofvelocities,determinedbythetemperatureofthewater.Eachmolecule followedaparticulartrajectorywhenthemanjumpedintothetank.Itstrajectoryis definedbyitspositionandvelocitythroughoutatimeinterval,sayfromjustbefore hereachedthesurfaceofthewatertosometimeafterthewaterinthetankhas settleddownaroundhim.Toreversehisfalleachwatermoleculewouldhavetofollow thesametrajectorybutinreverse.Thatispossiblebutitisjustoneofverymany trajectorieseachmoleculecanfollow.Thetotalnumberofpossibletrajectoriesofall 1030 moleculesisahugenumber,butitisnotinfinite.Iftimewerereversed,itwould notviolatetheconservationofenergyifallwatermoleculesreversedtheirtrajectories resultingintheman’sejectionfromthewater.Butforthattohappenthewater moleculeswouldhavetofollowoneparticularsetof1030 moleculartrajectoriesfrom
Whenisamaterialstable?
atotalnumberofpossibletrajectoriesmuchlargerthan1030.Theprobabilityofthat happeningissosmallaseffectivelytobeimpossible5 .
Whatwearehominginonhereisthe irreversibility ofspontaneousornatural processes.Oncewehavestirredfreshmilkintoacupofteawefinditimpossibleto separatethem.Ifwerunhotandcoldwaterintoabathwecannotseparatethehot waterfromthecold.Whenwedeformapieceofmetal,suchasapaperclip,sothat ittakesonanewpermanentshapethemetalbecomesharderandwarmeranditwill notspontaneouslyreturntoitssofter,undeformedstate.Ifwebreakachinacupinto piecesitcannotbereturnedtoitsformerpristinestatebycarefullyputtingallthe piecesbacktogetheragain.Ifwedischargeacapacitorthrougharesistorthecharge decreasesandeventuallyreacheszero.Heatflowsfromregionsofhightemperatures toregionsoflowtemperaturesbutnotbackagain.Itistheirreversibilityofthese processesthatdefinesoursenseofthedirectionoftime.Althoughthefundamental equationsofmotionofatomsandmoleculesaresymmetricwithrespecttothereversal oftime,theUniverseisnot.
Inthermodynamicsthedegreeofirreversibilityofaprocessischaracterisedand quantifiedbysomethingcalled entropy.Inallirreversibleprocessestheentropyofthe systemanditssurroundingsincreases.Foraprocesstobereversiblethetotalchange ofentropyhastobezero.Ifthereisanegativechangeinentropysomewhereitis alwayscompensatedbyapositivechangeofentropyatleastaslargesomewhereelse. Thesecondlawofthermodynamicsmaybestatedinequivalentwaysasfollows:
• Noprocessispossibleinwhichtheonlyresultisthecompleteconversionofheat intowork.
• Noprocessispossibleinwhichtheonlyresultisthetransferofheatfromacolder toahotterbody.
Ina spontaneousprocess thesystemchangesinanaturalwayfromanon-equilibrium statetowardsanequilibriumstate.Itisonlywhenthesystemisinequilibriumthat theentropyisconstant.Ifthesystemisisolateditsentropyisthenamaximum.Ifthis werenottrueaspontaneouschangeintheisolatedsystemwouldincreaseitsentropy, andthereforethesystemcouldnothavebeenatequilibrium.Thermodynamicstells usonlyaboutthedirectionofchange,andtheultimatedestination.Thetimeittakes forthesechangestooccurisnotpredictedbyequilibriumthermodynamics.
5 Iftherewerean infinite numberofpossibletrajectoriesforthe1030 moleculesthentheprobabilityofthemanemergingfromthewaterinadrystateandreturningtohisoriginalpositionwould be1/∞ =0.Thereasonitisnotzero,albeitextremelysmall,isthatthereisalowerlimitonthedifferencebetweentwotrajectoriesforthemtobeclassifiedasdistinct.ThelimitissetbyHeisenberg’s uncertaintyrelationofquantumtheory.Itstatesthattheuncertaintyinameasurementofaposition coordinateofaparticlemultipliedbytheuncertaintyinameasurementofthecorrespondingmomentumcoordinateisatleastequaltothePlanckconstant, h =6 626 × 10 34 Js.Thisdiscretisesthe 6 × 1030 dimensionalspace(eachmoleculehas3positioncoordinatesand3momentumcoordinates) ofthemoleculartrajectoriesinto1030 cells,eachofvolume h3.Ifthepositionsandmomentaofa givenparticlefallwithinthesame h3 celltheymustbetreatedasthesame.Although h issmallitis notzero.Itfollowsthatthenumberofpossibletrajectoriesofeachmoleculeisaverylargenumber butitisnotinfinite.(ThisisthereasonwhythePlanckconstantappearsinthestatisticalmechanics ofparticlesobeyingclassicalphysics,eventhoughitisnormallyasignatureofquantumphysics.)
A reversibleprocess takesthesystemthroughacontinuoussequenceofequilibrium states.Thisisanunattainablelimitingprocessthatcanbeapproachedinrealityonly bymaintainingthesystemextremelyclosetoequilibrium.Suchaprocesscanbe exactlyreversedifitisdrivenveryslightlyinthereversedirection.Theprocesshasto becarriedoutextremelyslowlytoallowthewholesystemtore-equilibrateaftereach extremelysmallchange.Thechangeofentropyassociatedwithareversibleprocessis zerobecausethesystempassesthroughasequenceofonlyequilibriumstates.
Thechangeofentropyofanobjectwhichundergoesachangeofequilibriumstate, suchasaphasechangeorachangeoftemperature,isindependentofwhetherthe changeoccursreversiblyorirreversibly.Thatisbecausetheentropyoftheobjectis uniquelydefinedbythevariablesthatdefineitsequilibriumstate,suchastemperature, pressureandchemicalpotentials.Inachangeofequilibriumstatethechangeofentropy dependsonlyontheinitialandfinalstates,andnotonhowitgetsfromtheinitialto thefinalequilibriumstates.Thispropertyofentropyelevatesittoa functionofstate. Anypropertyofthesystemwhichisuniquelydefinedbyitsequilibriumstateiscalled afunctionofstate.Theinternalenergyisanotherexampleofafunctionofstate.
Inareversiblechangeofstatethechangeofentropyofthesurroundingsisthe negativeofthechangeofstateoftheobject.Thechangeofthetotalentropyisthen zero.Inanirreversiblechangeofstateofasystemthesumofthechangesofentropy intheobjectanditssurroundingsisalwaysgreaterthanzero,byanamountthat increaseswiththedegreeofirreversibility.Butinallcasesthechangeofentropy oftheobjectundergoingachangeofstateisthesameirrespectiveofthedegreeof irreversibilityofthechange.
Ifasmallquantityofheat δq istransferredtoanobjectreversiblytheincreaseof theentropyoftheobjectis defined by δq/T ,where T isthetemperatureoftheobject. Inthisdefinition δq hastobesmallingeneralbecauseotherwisethetemperatureof theobjectwillchangeafter δq hasbeenadded.Butiftheheattransferredislatent heatassociatedwithaphasechangethen δq canbetheentirelatentheatsincethe temperature T isconstantduringthephasechange.Iftheobjectlosesheat δq is negativeandtheentropyoftheobjectdecreases.
Sincetheinternalenergyofanobjectisafunctionofstateitchangesbythesame amountinachangeofstate,irrespectiveofwhetherthechangeoccursreversiblyor irreversibly.Ingeneralachangeofstateinvolvesboththeadditionorremovalofheat andworkbeingdoneonorbytheobject6.Onlythesumofthesetwocontributionsto thechangeofinternalenergyisindependentofwhetherthechangeoccursreversibly orirreversibly.Thismeansthatingeneraltheheatgainorlossandtheworkdoneon orbytheobjectarenotfunctionsofstate.
Supposewehaveanisolatedsysteminwhichtherearelocalvariationsintemperature.Ifasmallamountofheat δq leavesalocalregionwithtemperature T1 the entropyoftheregionchangesby δq/T1.Ifthequantityofheat δq istransferredto
6AJouleexpansionisaninterestingexceptiontothisstatement:anidealgasoccupieshalfa containerandisseparatedfromavacuumintheotherhalfbyaremovablepartition.Theentire containeristhermallyinsulated.Thepartitionisremovedandthegasquicklyoccupiesthewhole container.Noheatentersorleavesthegasandnoworkisdoneonorbythegas.Itsinternalenergy anditstemperatureremainthesame.However,asweshallseeinthenextsectionitsentropyincreases becauseitoccupiestwicethevolume.
8 Whenisamaterialstable?
aregionwherethetemperatureis T2 itsentropychangesby+δq/T2.Thechangeof thetotalentropyofthesystemis δq/T2 δq/T1.Thesecondlawsaysthatforthis processtooccurspontaneouslythetotalchangeofentropymustbepositive.Thatis trueprovided T1 >T2.Inotherwords,heatflowsspontaneouslyonlyfromregionsof highertemperaturetoregionsoflowertemperature,whichaccordswithourexperience.Thestateofmaximumentropyiswhenthetemperatureisconstantthroughout thesystem.Werecognisethisasaconditionforthermalequilibriuminanisolated system.
Thesecondlawrecognisesthatthereissomethinguniqueaboutheat.Itisquite easytoconvertpotentialenergyintoelectricalenergy,andtoconvertelectricalenergy backintopotentialenergy,albeitwithsomelossesduetofriction.Thisiswhatis donefrequentlyatDinorwigpowerstation7 inSnowdonia,NorthWales.Conversions betweenotherformsofenergyarealsofeasible.Butnotwhenthefinalproductisheat. Forexample,whenanaircraftlandsmostofitskineticenergyendsupasheatinits brakes.Thatheatcannotbeusedtosendtheaircraftbackintotheair,despitethe firstlaw.Thesecondlawandourexperiencetellusthatwhenenergyisconvertedinto heatitisimpossibletoconvertallthatheatbackintowork.Thisisoftendescribedas the‘degradation’ofenergy.Asweshallseeinthenextsectionstatisticalmechanics explainsthispropertyofheatintermsofthe dispersal ofenergyamongmicrostatesof thesystem.Asenergybecomesmoredisperseditbecomeslesscapableofdoingwork, suchaspropellinganaircraftintotheair.
1.5.2Entropyintermsofmicrostates
Wehaveseeninsection 1.3 thatthethermodynamicstateofanisolatedsystemis expressedintermsofstatevariablessuchaspressure,volumeandtemperature.These aremacroscopicvariablesandtheydefinethe macrostate ofthesystem.AsIdiscussin Chapter 3,ifwewereabletolookinsideoneofthesemacrostatesattheatomicscalewe wouldseeatomsinconstantmotion.Ifthereare N atomsintheisolatedsystemthere are3N variablesassociatedwiththeirpositionsandanother3N variablesassociated withtheirinstantaneousvelocities8.These6N variablesconstitutea microstate ofthe system.Toeachmacrostateofthesystemthereisaverylargenumberofpossible microstates9.Butsomemacrostatesmayhavemanymoremicrostatesthanothers. Forexamplewhenacrystalmeltstheliquidstatehasmanymoremicrostatesthan thecrystalbecausetheatomsarenolongerconfinedtotheiraveragepositionswithin thecrystal.
Theconceptofentropywasintroducedatatimewhennoteveryonebelieved matterwasmadeofatoms.Itsderivationinclassicalthermodynamicsinvolves‘Carnot cycles’and‘heatengines’anditissomewhatabstract.ItwasLudwigBoltzmannwho providedamorephysicalunderstandingofentropy.Boltzmannshowedthatentropy increaseswiththenumber W of microstates ofanisolatedsystem,giventhatthe internalenergy,numbersofparticlesofeachspeciesandvolumeandshapeofthe
7https://www.electricmountain.co.uk/Dinorwig-Power-Station
8Thefactorsof3arisefromthe3spatialdimensionsofthesystem.
9Althoughthenumberofmicrostatesisverylargeitisnotinfiniteforthequantummechanical reasonexplainedinfootnote 5.
Thesecondlawofthermodynamics 9 systemareallconstant.Ifitisassumedthateachmicrostateisequallyprobable Boltzmannshowedthattheentropy S isproportionaltothelogarithmofthenumber W ofmicrostatesofthesystem:
= kB logeW
wheretheconstantofproportionality kB isthe Boltzmannconstant equalto1 381 × 10 23 Joulesperkelvin(JK 1).TheBoltzmannconstantisthegasconstant10 , R = 8.314JK 1,dividedbyAvogadro’snumber, NA =6.022 × 1023.Ifthereisanincreaseinentropyassociatedwithachangeofmacrostateofanisolatedsystem,the newmacrostatehasalargernumberofmicrostatesinwhichitcanexist.Thisiswhat ismeantbysayingthattheinternalenergyisdispersedoveralargernumberofmicrostateswhentheentropyincreases.Itdoesnotmeanthatatanygiveninstantintime theinternalenergyisdistributedamongmorecoexistingmicrostates.Itmeansthere aremoremicrostatesavailablefromwhichoneisselectedfortheentiremacrostateat anygiveninstantintime.
Itisnotdifficulttoseewhytheentropyhastodependonthe logarithm ofthe numberofmicrostates.ConsidertwoisolatedsystemsAandBatthesametemperature.LetthenumberofmicrostatesofsystemAbe WA andofsystemBbe WB .The entropiesoftheseparatesystemsare SA = kB logeWA and SB = kB logeWB .Suppose thetwosystemsarebroughtintothermalcontacttomakeasinglecombinedsystem, whilemaintainingabarrierbetweenthemtopreventtheircontentsfrommixing.Since thetwosystemsAandBareatthesametemperaturenoheatflowsbetweenthem. Withnoheatflowbetweenthem,andnointermixingoftheircontents,theentropyof thecombinedsystemisthesameasthetotalentropyoftheseparatesystemsAand B.Thetotalentropyoftheseparatesystemsis SA + SB = kB logeWA + kB logeWB Thenumberofmicrostatesofthecombinedsystemis WAWB ,andthereforeitsentropyis kB loge(WAWB ).Theseexpressionsareindeedequaltoeachotherbecause loge(WAWB )=logeWA +logeWB .Onlythelogarithmhasthisproperty.
Inanidealgasatconstanttemperaturethenumberofmicrostatesavailableisproportionaltothevolumeofthegasbecauseeachgasparticleisfreetoroamthroughout thevolume.Thereforetheentropyofanidealgasatconstanttemperatureisproportionaltothelogarithmofthevolumeitoccupies.Thisiswhytheentropyofthegasin aJouleexpansionincreases(seefootnote 6).Incontrast,atomsinasolidareconfined bytheirneighbourstomoveinmuchsmallervolumesthanthetotalvolumeofthe solid.Theyvibrateabouttheirequilibriumpositions,andthemicrostatesavailableto thematconstanttemperatureincreasewiththeiramplitudesofvibration.Therefore, atomsinlessconfined,moreopenspacesinagivensolidcontributemoretothetotal entropyofthesolidthanatomsinmoreconfinedenvironments.Theseideascarryover toexoticmaterialssuchascolloidswhereparticlesthataresmallbutmuchlargerthan atomsareheldinsuspensioninaliquid.Itisfoundthatinertspheressuspendedin
10thegasconstantis R intheequationofstateofanidealgas PV = nRT ,where P isthegas pressuremeasuredinpascals, V itsvolumeincubicmetres, T itstemperatureinkelvinand n isthe amountofthegasinmoles.
S
aliquidmaysometimescrystalliseinstructuresthatarenotdenselypacked.These openstructuresarestabilisednotbypotentialenergybutbytheirhigherentropy11
1.5.3Configurationalentropy
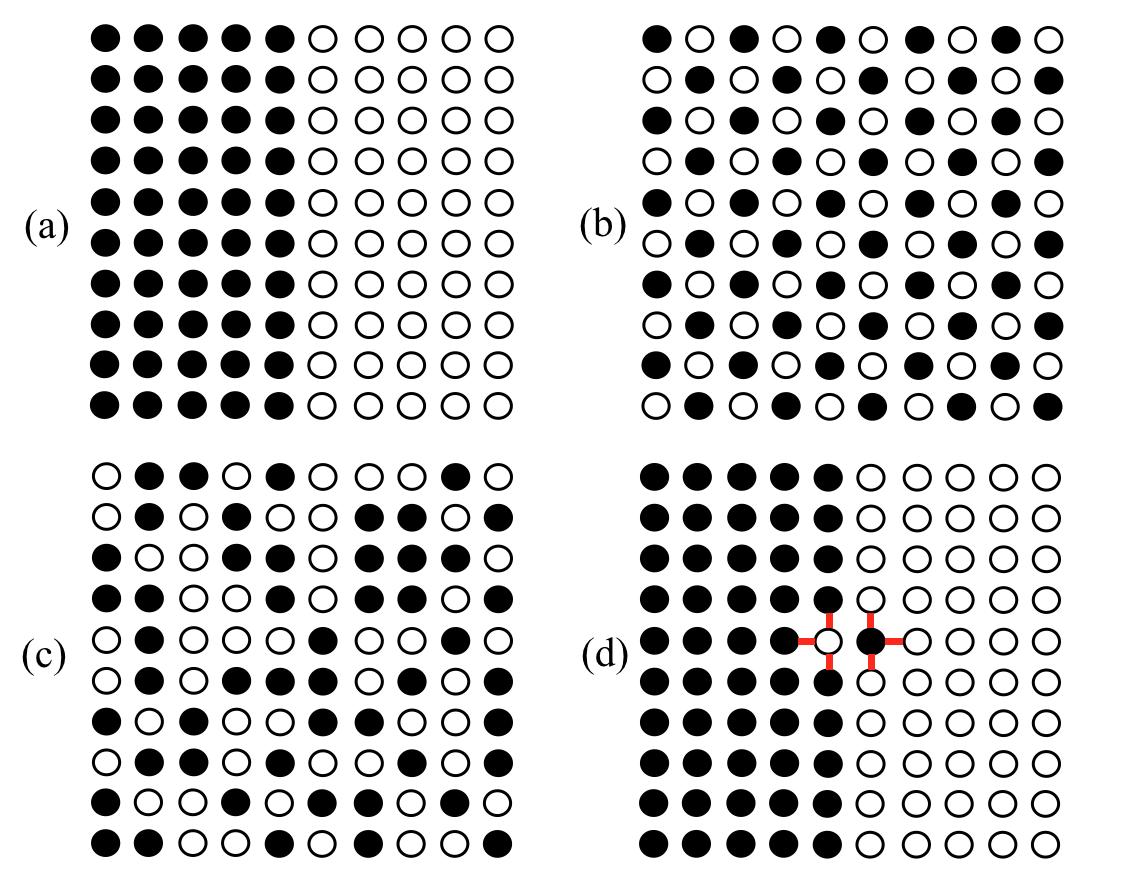
Theentropyofanisolatedsystemmayalsoincreaseastheresultofmixingdistinguishableatomstogether.Thisiscalled configurationalentropy.Asasimpleexample, considerahypotheticalsquaretwo-dimensionalcrystalwithasquarelattice,comprising10 × 10latticesites.Forsimplicityweshallignoretheatomicvelocitiesinthis example.Eachofthe100latticesitesmaybeoccupiedbyeitherablackatomora whiteatom.Thecolourdenoteseitheradistinctisotopeofthesameelement,suchas carbon-12andcarbon-14,oratomsoftwoelements.Lettherebe50blackatomsand 50whiteatomsarrangedonthe100sites.Thereisa‘maximallyseparated’stateas showninFig. 1.1a.Thereisalsoa‘maximallyintermixed’statewherethefourneighboursofeachblackatomarewhiteand viceversa,asshowninFig. 1.1b.Fig. 1.1c illustratesaconfigurationwherethe100atomicsitesareoccupiedrandomlyby50 blackand50whiteatoms.Itisanamazingfactthattherearearound1029 similar randomconfigurationsof50blackand50whiteatomsonthese100latticesites12.Each oftheconfigurationsshowninFig. 1.1 isamicrostateofthecrystalof100atoms. Iftheblackandwhiteatomsareisotopesofthesameatomthepotentialenergiesof alltheseconfigurationsareequal,becausetheenergiesofthebondsbetweenatomsare independentofthenumberofneutronsineachatomicnucleus.Atalltemperaturesup tothemeltingpointtheentropyismaximisedwhenthecrystalisdisorderedbecause all1029 configurationsareequallyaccessible,andtheoverwhelmingmajorityofthem aredisordered.Inarealcrystalwithmanymorethan100atomicsitesthenumberof possiblerandomatomicconfigurationsincreasesrapidly.Thisiswhyitwassodifficult toseparatetheisotopesofuraniumintheManhattanProjecttodeveloptheatomic bomb.
Supposebondsbetweenatomsofthesamecolourareoflowerpotentialenergythan thosebetweenatomsofdifferentcolours.Thepotentialenergyofthesystemisminimisedwhenthenumberofbondsbetweenblackandwhiteatomsisminimised.This correspondstotheconfigurationofFig. 1.1a.Thereareafurtherthreeconfigurations equivalenttoFig. 1.1aobtainedbyrotatingthewholecrystalaboutthenormaltothe pageby90◦ , 180◦ and270◦.AnydeviationfromtheconfigurationshowninFig. 1.1a requiresenergy,butifthereisnoheatintheisolatedsystemnosuchdeviationsare permittedbythefirstlaw.Theconfigurationalentropyisthen kB loge4becausethere arefourequivalentconfigurations.
ImagineweheatthesystemdepictedinFig. 1.1arapidlytoalowtemperature andthenisolateit.Thenewequilibriumstateoftheisolatedsystemisdetermined bymaximisingtheentropyattheslightlyhigherinternalenergy.Anexchangeof neighbouringblackandwhiteatomsattheinterfaceraisesthepotentialenergyofthe systembecauseitincreasesthenumberofbondsbetweenatomsofdifferentcolours
11Mao,X,Chen,QandGranick,S,NatureMater 12,217(2013).
12Thetotalnumberofconfigurationsisthebinomialcoefficient 100C50 =100!/(50!)2.Thenumber ofrandomconfigurationsis6lessthan 100C50 becausethereare4configurationslikeFig. 1.1aand 2configurationslikeFig. 1.1b.
Fig.1.1 Fouratomicconfigurationsofa10 × 10squarecrystallattice,with50‘black’atoms and50‘white’atomsoccupyingthe100latticesites.(a)themostseparatedstate.(b)the mostintermixedstate.(c)oneofthe ≈ 1029 configurationswithsitesoccupiedbyblackand whiteatomsatrandom.(d)theatomicconfigurationshownin(a)withoneexchangebetween blackandwhiteatomsattheinterface.Theexchangeintroduces6newbonds,showninred, betweenblackandwhiteatoms.
bysix,asshowninFig. 1.1d.Providedthereissufficientheatinthecrystaltosupply thisincreaseofpotentialenergyalocalthermalfluctuationcanenabletheexchange tooccur,atleastinprinciple.Theadditionalpotentialenergyofthenewbondsis accompaniedbyareductioninthekineticenergyofthesystem,maintainingaconstant valueoftheinternalenergy.Thepairofexchangedatomsattheinterfacemayproceed toexchangewithotheratomswithnofurtherincreaseofpotentialenergy.Thus, onceanexchangehasoccurredattheinterfacetheexchangedwhiteatomcanoccupy anyofthe50blackatomsitesofFig. 1.1d.Similarly,theexchangedblackatomcan occupyanyofthe50whiteatomsites.Thusoneexchangeattheinterfaceleads to50 × 50=2, 500newconfigurationsthatsharethesamepotentialenergy.The configurationalentropyhasincreasedasaresultofthisoneexchangeattheinterface. Furtherexchangescantakeplaceifthereissufficientheatinthesystem.Atequilibriumtheatomicstructureofthesystemisnotconstantintimebutisrunningthrough alltheaccessiblestatesatthegiveninternalenergy.Astheatomicstructurechanges thetotalpotentialenergyofthebondschangestoo.Thetemperatureofthesystem hastochangetomaintainconstanttheinternalenergy.Theaveragetemperaturewill settledowntoavalueatequilibriumthatislessthanthetemperatureofthesystem beforeitequilibrated.Furtherinjectionofheatintothesystemwilleventuallyenable all1029 configurationstobecomeaccessible.AlthoughthestateshowninFig. 1.1a,or
Whenisamaterialstable?
oneofthethreeequivalentconfigurations,continuestohavethelowestpotentialenergyitisextremelyunlikelytoarisewhentherearesomanymoreaccessibledisordered configurationslikeFig. 1.1c.
The‘mostintermixed’configurationshowninFig. 1.1barisesatlowtemperatures whenbondsbetweenatomsofdifferentcolourshavealowerpotentialenergythanthose betweenatomsofthesamecolour13.Asthecrystalisheatedanincreasingnumber ofatomicexchangesmaytakeplaceuntileventuallyall1029 randomconfigurations becomeaccessible,assumingitdoesnotmeltfirst.Thustheequilibriumconfiguration ofthecrystalathightemperaturesisanaveragetakenoverall1029 configurations, almostallofwhicharerandom.Inthisstateiftheatomsreallywerecolouredblack andwhitetheywouldallappeargreyinatime-lapsephotograph–halfwaybetween blackandwhite.
1.5.4Summaryofsection 1.5
Theirreversibilityofspontaneous,naturalprocessesimposesadirectionontime.Such processesarealwaysassociatedwithanincreaseofentropyinthesystemandits surroundings:thisisthesecondlawofthermodynamics.Thegreatertheincreaseof entropythegreaterthedegreeofirreversibility.Onlyreversibleprocessescreateno entropy.Inanisolatedsystementropyisdirectlyrelatedtothenumberofmicrostates thesystemcanaccesswiththeinternalenergythesystemhas.Theirreversibility ofconvertingworkintoheatiscausedbythedispersaloftheenergyamongavery largenumberofmicrostatesofthesystem.Thisdispersalissometimescalledthe ‘degradationofenergy’:energyisconservedwhenitisconvertedintoheatbutitis lesscapableofdoingwork.
1.6Closedsystemsandheatreservoirs
Sofarwehaveconsideredtheentropyofonlyisolatedsystems.Inaclosedsystem theobjectwearestudyingcanexchangeheatwiththeenvironment,butitcannot exchangematter.Totreataclosedsystemweimaginetheobjectofstudyisinthermal contactwithalargeheatreservoirataconstanttemperature Tr.Theroleoftheheat reservoiristoacceptordonateheattokeeptheobjectataconstanttemperatureof Tr.Intheprocessitisassumedtherearenoirreversiblechangesofentropywithinthe reservoirsuchasmixingorchemicalreactions.Thereservoirisinastateofinternal equilibrium.Undertheseconditionsiftheheatreservoirdonatesasmallamountof heat δqrev totheobjectitundergoesareversiblechangeofstateandtheentropy ofthereservoirchangesby δSres = δqrev/Tr.Iftheobjectacceptstheheat δqrev reversiblyitsentropychangesby+δqrev/Tr.Thus,inareversibletransferofheatthe totalchangeofentropyiszero.
Inareversibletransferofheat δqrev fromthereservoirtotheobjecttheinternal energyoftheobjectincreasesby δU = δqrev.Thatisbecausenoworkisdonebyor ontheobjectwhenthechangeofstateinvolvesatransferofheatonly.Butsuppose
13Notethereareblackatomsatthetopleftandbottomrightcornersandwhiteatomsatthetop rightandbottomleftcorners.Thereisanequivalentconfiguration,obtainedbyrotatingthecrystal by ±90◦ aboutthenormaltothepage,wherethepositionsofalltheblackandallthewhiteatoms areinterchanged.Therefore,theentropyofthisconfigurationis kB loge2.
TheHelmholtzfreeenergy 13
thesamechangeofinternalenergy δU = δqrev oftheobjectisbroughtaboutby an irreversible changeofitsstateinwhichwork δw isdoneonitinadditiontoa transferofheat δqirrev.Therefore, δU = δqrev = δqirrev + δw.Thechangeofentropy ofthereservoiris δSres = δqirrev/Tr becauseithaslostheat δqirrev andallchanges ofheatcontentofthereservoiroccurreversibly.Sincetheobjecthasundergonethe samechangeofstateitschangeofentropyremains δSobj = δqrev/Tr becauseentropy isafunctionofstate.Sincethechangeofstateisnowirreversibleitmustbetrue that δSres + δSobj > 0,andtherefore δqrev >δqirrev.Thedifference δqrev δqirrev is providedbythework δw doneontheobjectwhichisdegradedtoheatintheobject.
Ontheotherhand,ifthechangeofstateinvolvesatransferofheatfromtheobject tothereservoir,moreheatistransferredifthechangeofstateoccursirreversiblythan ifitoccursreversibly.Let δqrev and δqirrev betheamountsofheattransferredfrom theobjecttothereservoirinreversibleandirreversiblechangesofstaterespectively. Thechangeintheentropyoftheobjectis δSobj = δqrev/Tr regardlessofwhetherthe changeofstateoccursreversiblyorirreversibly.Thechangeofentropyofthereservoir is δSres =+δqirrev/Tr.Therefore,thetotalchangeofentropyis(δqirrev δqrev)/Tr whichmustbepositive.Thedifference δqirrev δqrev istheworkdonebytheobject thatisdegradedtoheatinthereservoir.
Inbothcasesworkisdegradedtoheatwhenthechangeofstateoccursirreversibly.
1.7TheHelmholtzfreeenergy
Wehaveseenthatinanisolatedsystemequilibriumisachievedwhentheentropy ofthesystemismaximised.Asanisolatedsystemevolvestowardsequilibriumits temperaturechanges.Itismoreusefultohaveacriterionforequilibriuminaclosed systemwherethetemperatureiskeptconstantbyplacingtheobjectincontactwitha thermalreservoir.However,noparticlesleaveorentertheobject.Nevertheless,there canstillbemovementofparticlesandchemicalreactionswithintheobjectresulting innewphases.TheequilibriumcriterionisprovidedbytheHelmholtzfreeenergy, whichisafunctionofinternalenergy,entropyandtemperatureandthereforeitisa functionofstate.
Incaseyouarewonderingwhether‘free’energyistheanswertotheproblemsof theWorld’senergysupplythereisnosuchthingasenergywithoutaneconomiccost. Theuseoftheword‘free’inthiscontextisquitedifferent.Asweshallseeitmeans themaximumenergyavailabletodoworkinasystemheldataconstanttemperature. Betterdescriptorswouldbe‘availablework’or‘usefulenergy’,butwearestuckwith ‘freeenergy’becauseithasbecomecommonusage.
TheHelmholtzfreeenergy A isdefinedastheinternalenergy U minusthetemperature T timestheentropy S,thus A = U TS.Consideranobjectimmersedin alargeheatreservoiratatemperature Tr.Lettheobjectundergoachangefroma statelabelled‘1’toastatelabelled‘2’.TheHelmholtzfreeenergyoftheobjectin state1is A1 = U1 TrS1 andinstate2itis A2 = U2 TrS2.Lettheamountofheat enteringtheobjectingoingfromstate1to2be q.Lettheworkdonebytheobject ingoingfromstate1to2be w.Then U2 U1 = q w.Sincetheinternalenergyisa functionofstate, U2 U1 isindependentofthedegreeofirreversibilityofthechange ofstate.But q and w dodependonthedegreeofirreversibilityinsuchawaythat