CombinatorialPhysics:Combinatorics,Quantum FieldTheory,andQuantumGravityModelsAdrian Tanasa
https://ebookmass.com/product/combinatorial-physicscombinatorics-quantum-field-theory-and-quantum-gravitymodels-adrian-tanasa/
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Introduction to Quantum Field Theory with Applications to Quantum Gravity 1st Edition Iosif L. Buchbinder https://ebookmass.com/product/introduction-to-quantum-field-theorywith-applications-to-quantum-gravity-1st-edition-iosif-l-buchbinder/ ebookmass.com
Quantum Field Theory and Critical Phenomena 5th Edition Jean Zinn-Justin
https://ebookmass.com/product/quantum-field-theory-and-criticalphenomena-5th-edition-jean-zinn-justin/
ebookmass.com
Quantum Space: Loop Quantum Gravity and the Search for the Structure of Space, Time, and the Universe Baggott
https://ebookmass.com/product/quantum-space-loop-quantum-gravity-andthe-search-for-the-structure-of-space-time-and-the-universe-baggott/ ebookmass.com
Modern Information Optics with MATLAB Yaping Zhang
https://ebookmass.com/product/modern-information-optics-with-matlabyaping-zhang/
ebookmass.com
Someday Away Sara Elisabeth https://ebookmass.com/product/someday-away-sara-elisabeth/
ebookmass.com
Window on Humanity: A Concise Introduction to General Anthropology 8th Edition, (Ebook PDF)
https://ebookmass.com/product/window-on-humanity-a-conciseintroduction-to-general-anthropology-8th-edition-ebook-pdf/
ebookmass.com
Diagnostic Imaging: Brain 4th Edition Miral D. Jhaveri
https://ebookmass.com/product/diagnostic-imaging-brain-4th-editionmiral-d-jhaveri/
ebookmass.com
Pediatrics Morning Report: Beyond the Pearls 1st Edition Adler Salazar
https://ebookmass.com/product/pediatrics-morning-report-beyond-thepearls-1st-edition-adler-salazar/
ebookmass.com
Corporate spirit: religion and the rise of the modern corporation Amanda Porterfield
https://ebookmass.com/product/corporate-spirit-religion-and-the-riseof-the-modern-corporation-amanda-porterfield/
ebookmass.com
https://ebookmass.com/product/hegels-interpretation-of-the-religionsof-the-world-the-logic-of-the-gods-jon-stewart/
ebookmass.com
COMBINATORIALPHYSICS CombinatorialPhysics Combinatorics,quantumfieldtheory,andquantum
gravitymodels
AdrianTanasa
UniversityofBordeaux,France
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries
©AdrianTanasa2021
Themoralrightsoftheauthorhavebeenasserted
FirstEditionpublishedin2021 Impression:1
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica
BritishLibraryCataloguinginPublicationData Dataavailable
LibraryofCongressControlNumber:2021932400 ISBN978–0–19–289549–3 DOI:10.1093/oso/9780192895493.001.0001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
ToLuca,Brittany,andtoourfamily
2.1Graphtheory:TheTuttepolynomial7
2.2Ribbongraphs;theBollobás–Riordanpolynomial12
2.3Selectedfurtherreading15
3Quantumfieldtheory(QFT)—built-incombinatorics 17
3.1Definitionofthescalar Φ4 model18
3.2Perturbativeexpansion—Feynmangraphsandtheircombinatorialweights20
3.3Fouriertransform—themomentumspace23
3.4ParametricrepresentationofFeynmanintegrands24
3.5Thepropagatorandtheheatkernel26
3.6Aglimpseofperturbativerenormalization27
3.6.1Thepowercountingtheorem29
3.6.2Locality30
3.6.3Multi-scaleanalysis32
3.6.4ThesubtractionoperatorforageneralFeynmangraph33
3.6.5Dimensionalrenormalization35
3.7Dyson–Schwingerequation36
3.8Combinatorial(or 0-dimensional)QFTandtheintermediatefieldmethod36
3.8.1Combinatorial(or 0-dimensional)QFT36
3.8.2Theintermediatefieldmethod37 3.9Selectedfurtherreading38
4.1Preliminaryresults41 4.2Partitiontreeweights43 4.3Selectedfurtherreading49
5.1TheJacobianConjectureascombinatorialQFTmodel (theAbdesselam–Rivasseaumodel)52
5.2TheintermediatefieldmethodfortheAbdesselam–Rivasseaumodel53
5.3Selectedfurtherreading55
6FermionicQFT,Grassmanncalculus,andcombinatorics 56
6.1GrassmannalgebrasandGrassmanncalculus57
6.1.1TheGrassmannalgebra57
6.1.2Grassmanncalculus;PfaffiansasGrassmannintegrals58
6.2OnGrassmannGaussianmeasures59
6.3Lingström–Gessel–Viennot(LGV)formulaforgraphswithcycles60
6.4Stembridge’sformulasforgraphswithcycles63
6.5Ageneralization66
6.6TuttepolynomialandtheparametricrepresentationinQFT67
6.7Selectedfurtherreading71
7AnalyticcombinatoricsandQFT
8.1Algebraicreminder;CombinatorialHopfAlgebras(CHAs)77
8.2TheConnes–KreimerHopfalgebraofFeynmangraphs79
8.3The B+ operator,HochschildcohomologyoftheConnes–Kreimeralgebra83
8.4Multi-scalerenormalization,CHAdescription85
8.5Selectedfurtherreading94
9QFTonthenon-commutativeMoyalspaceandcombinatorics 95
9.1Mathematicalsetting:Renormalizability96
9.2TheMehlerkernelandtheGrosse–Wulkenhaarmodel99
9.3ParametricrepresentationofGrosse–Wulkenhaar-likemodels100
9.4TheMellintransformandtheGrosse–Wulkenhaarmodel104
9.5DimensionalrenormalizationfortheGrosse–Wulkenhaarmodel107
9.6Aheatkernel–basedrenormalizablemodel108
9.7ParametricrepresentationandtheBollobás–Riordanpolynomial110
9.7.1Parametricrepresentation110
9.7.2Relationbetweenthemulti-variateBollobás–Riordanandthe polynomialsoftheparametricrepresentation111
9.8CombinatorialConnes–KreimerHopfalgebraandits Hochschildcohomology112
9.8.1CombinatorialConnes–KreimerHopfalgebra112
9.8.2HochschildcohomologyandthecombinatorialDSE117
9.9Selectedfurtherreading120
10Quantumgravity,groupfieldtheory(GFT),andcombinatorics 121
10.1Quantumgravity121
10.2Maincandidatesforatheoryofquantumgravity:Theholographicprinciple122
10.3GFTmodels:theBoulatovandthecolourablemodels123
10.4Themulti-orientableGFTmodel125
10.4.1Tadpolesandgeneralizedtadpoles127
10.4.2Tadfaces128
10.5SaddlepointmethodforGFTFeynmanintegrals129
10.6AlgebraiccombinatoricsandtensorialGFT133
10.6.1TheBenGeloun–Rivasseau(BGR)model133
10.6.2Cones–KreimerHopfalgebraicdescriptionofthecombinatorics oftherenormalizabilityoftheBGRmodel143
10.6.3HochschildcohomologyandthecombinatorialDSE fortensorialGFT153
10.7Selectedfurtherreading165
11Fromrandommatricestorandomtensors 166
11.1Thelarge N limit169
11.2Thedouble-scalinglimit169
11.3Frommatricestotensors170
11.4Tensorgraphpolynomials—ageneralizationoftheBollobás–Riordan polynomial174
11.5Selectedfurtherreading176
12Randomtensormodels—the U (N )D -invariantmodel 178
12.1DefinitionofthemodelanditsDSE179
12.1.1 U(N)D -invariantbubbleinteractions179
12.1.2Bubbleobservables182
12.1.3TheDSEforthemodel185
12.1.4Navigatingthefollowingsectionsofthechapter187
12.2TheDSEbeyondthelarge N limit188
12.2.1TheLO188
12.2.2MomentsandCumulants189
12.2.3Gaussianandnon-Gaussiancontributions192
12.2.4TheDSEatNLO198
12.2.5Theorder 1/N D inthequarticmodel199
12.3Thedouble-scalinglimit202
12.3.1Double-scalinglimitintheDSE202
12.3.2Fromthequarticmodeltoagenericmodel206
12.4Selectedfurtherreading208
13Randomtensormodels—themulti-orientable(MO)model 209
13.1Definitionofthemodel209
13.2The 1/N expansionandthelarge N limit212
13.2.1Feynmanamplitudes;the 1/N expansion212
13.2.2Thelarge N limit—theLO(melonicgraphs)214
13.2.3Thelarge N limit—theNLO215
13.2.4LeadingandNLOseries216
13.3Combinatorialanalysisofthegeneraltermofthelarge N expansion219
13.3.1Dipoles,chains,schemes,andallthat220
13.3.2Generatingfunctions,asymptoticenumeration, anddominantschemes226
13.4Thedouble-scalinglimit230
13.4.1Thetwo-pointfunction231
13.4.2Thefour-pointfunction232
13.4.3The 2r -pointfunction232
13.5Selectedfurtherreading233 14Randomtensormodels—the
14.1Generalmodelandlarge N expansion234
14.2Quarticmodel,large N expansion241
14.2.1LargeNexpansion:LO242
14.2.2NLO247
14.3Generalquarticmodel:Criticalbehaviour248
14.3.1Explicitcountingofmelonicgraphs248
14.3.2Diagrammaticequations,LOandNLO252
14.3.3Singularityanalysis253
14.3.4Criticalexponents256
14.4Selectedfurtherreading259
15TheSachdev–Ye–Kitaev(SYK)holographicmodel
15.1DefinitionoftheSYKmodel:ItsFeynmangraphs261
15.2Diagrammaticproofofthelarge N melonicdominance264
15.3ThecolouredSYKmodel271
15.3.1Definitionofthemodel,real,andcomplexversions271
15.3.2Diagrammaticsoftherealandcomplexmodel272
15.3.3MoreonthecolouredSYKFeynmangraphs282
15.3.4Non-Gaussiandisorderaverageinthecomplexmodel284
15.4Selectedfurtherreading290
16SYK-liketensormodels 291
16.1TheGurau–Wittenmodelanditsdiagrammatics292
16.1.1Two-pointfunctions:LO,NLO,andsoon293
16.1.2Four-pointfunction:LO,NLO,andsoon295
16.2The O (N )3 -invariantSYK-liketensormodel300
16.3TheMOSYK-liketensormodel303
16.4RelatingMOgraphsto O (N )3 -invariantgraphs304
16.5Diagrammatictechniquesfor O (N )3 -invariantgraphs306
16.5.1Two-edge-cuts306
16.5.2Dipoleremovals307
16.5.3Dipoleinsertions309
16.5.4Chainsofdipoles310
16.5.5Facelength312
16.5.6Thestrategy314
16.6Degree 1 graphsofthe O (N )3 -invariantSYK-liketensormodel316
16.6.12PI,dipole-freegraphofdegreeone316
16.6.2Thegraphsofdegree1319
16.7Degree 3/2 graphsofthe O (N )3 -invariantSYK-liketensormodel323
AExamplesoftreeweights
A.1Symmetricweights—completepartition331
A.2Onesingletonpartition—rootedgraph332
A.3Twosingletonpartition—multi-rootedgraph333
BRenormalizationoftheGrosse–Wulkenhaarmodel,one-loopexamples
CThe B + operatorinMoyalQFT,two-loopexamples
C.1One-loopanalysis338 C.2Two-loopanalysis338
DExplicitexamplesofGFTtensorFeynmanintegralcomputations
D.1Anon-colourable,MOtensorgraphintegral345
D.2Acolourable,multi-orientabletensorgraphintegral345
D.3Anon-colourable,non-multi-orientabletensorgraphintegral347
G.1Bijectionwithconstellations362
G.1.1Bijectioninthebipartitecase362
G.1.2Thenon-bipartitecase365
G.2Enumerationofcolouredgraphsoffixedorder366
G.2.1Exactenumeration366
G.2.2Singularityanalysis369
G.3TheconnectivityconditionandSYKgraphs371
G.3.1Preliminaryconditions371
G.3.2Thecase q> 3
G.3.3Thecase q =3
G.3.4Thenon-bipartitecase374 HProofofTheorem16.1.1
ISummaryofresultsonthediagrammaticsofthecolouredSYK modelandoftheGur ˘ au–Wittenmodel
Introduction Theinterplaybetweencombinatoricsandtheoreticalphysicsisarecenttrendwhich appearstousasparticularlynatural,sincetheunfoldingofnewideasinphysicsis oftentiedtothedevelopmentofcombinatorialmethods,and,conversely,problems incombinatoricshavebeensuccessfullytackledusingmethodsinspiredbytheoretical physics.Alotofproblemsinphysicsarethusrevealedtobeenumerative.Ontheother hand,problemsincombinatoricscanbesolvedinanelegantwayusingtheoretical physics-inspiredtechniques.Wecanthusspeaknowadaysofanemergingdomainof CombinatorialPhysics.
Theinterferencebetweenthesetwodisciplinesismoreoveraninterferenceofmultiple facets.Thus,itsmostknownmanifestation(bothtocombinatorialistsandtheoretical physicists)hassofarbeentheonebetweencombinatoricsandstatisticalphysics, orcombinatoricsandintegrablesystems,asstatisticalphysicsreliesonanaccurate counting ofthevariousstatesorconfigurationsofaphysicalsystem.
However,combinatoricsandtheoreticalphysicsinteractinvariousotherways.One oftheseinteractionsistheonebetweencombinatoricsandquantummechanics,because combinatorialtoolscanbeusedhereforabettermathematicalunderstandingofthe algebrasunderlyingquantummechanics.
Inthisbook,wemainlyfocusonyetanothertypeofthesemultipleinteractions betweencombinatoricsandtheoreticalphysics,theonebetweencombinatoricsand quantumfieldtheory(QFT).Weestimatethatcombinatoricsis builtinto themathematicalformulationofQFT.Thisstemsinitiallyfromthefactthatthemostpopular toolofQFTisperturbationtheoryinthecouplingconstantofthemodel,whichmeans thatoneconsidersFeynman graphs,withappropriatecombinatorialweights,inorderto encodethephysicalinformationoftherespectivesystem.Moreover,oneelegantwayof expressingtheFeynmanintegralsassociatedwiththesegraphsistousetheKirchhoff–Symanzikpolynomialsoftheparametricrepresentation,polynomialswhichcanbe proventoberelatedtosomemulti-variateversionofthecelebratedTuttepolynomial ofcombinatorics.Aparticularlyelegantwaytoprovethisistousethe Grassmann development ofthedeterminantsandPfaffiansinvolvedinthesecomputations.Letus emphasizeherethatthisGrassmanndevelopmentusesGrassmanncalculus,whichwere developedbyphysiciststoexpressfermionicQFT.Grassmanncalculusisfurtherusedin thisbooktogiveasimpleproofofthecelebratedLingström–Gessel–Viennot(forgraphs
Introduction withcycles)andtofurthergeneralizesomeidentities,initiallyprovedbyStembridge,in thesamecontextofgraphswithcycles.
Theso-called 0 dimensionalQFT(calledbysomeauthors,combinatorialQFT),or morepreciselytheuseoftheintermediatefieldmethodinthissetting,allowstoestablisha theoremconcerningpartialeliminationofvariablesinthecelebratedJacobianconjecture (whichconcernstheglobalinvertibilityofpolynomialsystems).
Moreover, analyticcombinatorial techniquesareusedonaregularbasisinQFT computations.Thus,thepropagatorofanyscalarmodelcanberepresentedusingthe heatkernel.TheMellintransformtechniquecanalsobeusedinordertorapidlyprove themeromorphyofFeynmanintegrands.Thesaddlepointmethodisfrequentlyusedto tamethedivergentbehaviouroftheseintegrals.
Lastbutnotleast,renormalizationinQFT(whichonecansayliesattheveryheartof QFT)hasahighlynon-trivialcombinatorialcore,andthishasbeenrecentlypresented ina combinatorialHopfalgebra form—theConnes–KreimerHopfalgebra.Relatedtothis, theHochschildcohomologyofthiscombinatorialHopfalgebracanbeusedtoexpress thecombinatoricsoftheDyson–Schwingerequation(DSE)asasimplepowerseriesin someappropriateinsertionoperatorofFeynmangraphs.
Allthesecombinatorialtechniques(analyticoralgebraic)generalizetomoreinvolved QFTmodels.Thus,non-commutativeQFT(thatis,QFTonanon-commutativespacetime)alsopossessesmostofthesecombinatorialproperties.First,thegraphsusedin QFTareupliftedtoribbongraphs(or combinatorialmaps).Furthermore,onecanstill usetheheatkernelforpropagatorsofthetheories,butinordertohaverenormalizable models,oneneedstouseamoreinvolvedspecialfunction,theMehlerkernelorsome non-trivialmodificationoftheheatkernel.Moreover,theMellintransformtechniquecan againbeused,asinthecaseofcommutativeQFT.Thecorrespondingnon-commutative Kirchhoff–Symanzikpolynomialsareproventobealimitofamulti-variateversionof theBollobás–Riordanpolynomial(whichisanaturalgeneralizationforribbongraphs oftheuniversalTuttepolynomial).Finally,algebraiccombinatorialtechniquescanalso beusedinnon-commutativeQFT.ThecorrespondingcombinatorialConnes–Kreimer HopfalgebraofribbonFeynmangraphscanbedefinedandrelatedtonon-commutative renormalization.Furthermore,theappropriateHochschildcohomologythendescribes thecombinatoricsoftheDSEofthesemodels.
Non-commutativeQFTcanalsobeseenasaspecialcaseofthecelebratedmatrix models.Followingthislineofreasoning,onecannaturallygeneralizerandommatrix modelstorandomtensormodels,
Thecombinatoricsoftensormodelsperseisextremelyinvolved.Onecannot just use thegenustocharacterizetheso-calledlarge N expansion, N beingthesizeofthematrix resp.ofthetensor.Itisworthemphasizingherethatthelarge N expansionis,froma combinatorialpointofview,acertainasymptoticexpansion(correspondingtothelimit N →∞).
However,inordertomakethecombinatoricssimpler,severalQFT-inspiredsimplificationsoftensormodelscanbeproposed.Thefirsttwosuchsimplicationswerethe colouredmodelandthemulti-orientablemodels.Forbothofthesemodels,onecan implementthelarge N expansionandthedouble-scalingmechanism,which,inthecase
3 ofmatrixmodels,areveryimportantmathematicalphysicstools.Severalothermodels (basedon U (N ) andthen O (N ) modelshavealsobeenstudied.
Feynmangraphsassociatedtotensormodels,throughthecelebratedQFTperturbativeexpansions,arecalledtensorgraphsandcanbeseenasanatural3Dgeneralizationof mapsorofribbongraphs.Thedominanttermofthelarge N expansionofthepreviously mentionedtensormodelsaretheso-calledmelonicgraphs,whichare,fromagraph theoreticalpointofview,aparticularcaseofseries-parallelgraphs.
Thelarge N expansioniscontrolledinthe2Dcase,thematrixmodelcase,bythe genusofthecorrespondingcombinatorialmaps.Indimensionhigherthantwo,there isnodirectanalogueofthegenus.Nevertheless,thetensorasymptoticexpansionin N iscontrolledbyaninteger,calledthedegree,whichisdefinedasthehalf-sumofthe non-orientablegenusofribbongraphscanonicallyembeddedinatensorgraph(called thejacketsoftherespectivetensorgraphs).Thedegreeisthusahalfinteger,naturally generalizingthe2Dnotionofgenusfortensormodels.
Inordertostudythegeneraltermofthelarge N expansionofvarioussuchtensor models,weextensivelyuse,inthisbook,variousgraphtheoreticaland enumerative combinatorics techniquestoperformtheirenumerationandweestablishwhicharethe dominantconfigurationsofagivendegree.
Itisworthemphasizingherethattensormodelshaverecentlybeenprovenby WittentoberelatedtothecelebratedholographicSachdev–Ye–Kitaev(SYK)quantum mechanicalmodel.Thiscomesfromthefactthat,intheso-calledlarge N expansion (N beinginthecaseoftheSYKmodelthetotalnumberoffermionsofthemodel), bothtypesofmodelsaredominatedbythemelonicgraphs.Thelarge N expansion forvariousSYK-liketensormodelsisthenstudiedusingagaingraphtheoreticaland enumerativecombinatoricstechniques.Thesetechniquesallowustoasymptotically enumerateFeynmangraphsofvariousSYK-liketensormodels.
Thebookisorganizedasfollows.InChapter 2,wepresentsomenotionsofgraph theorythatwillbeusefulintherestofthebook.Itisworthemphasizingthatgraph theoristsandtheoreticalphysicistsadopt,unfortunately,differentterminologies.We presentherebothterminologies,suchthatasortofdictionarybetweenthesetwo communitiescanbeestablished.Wethenextendthenotionofgraphtothatofmaps(or ofribbongraphs).Moreover,graphpolynomialsencodingthesestructures(theTutte polynomialforgraphsandtheBollobás–Riordanpolynomialforribbongraphs)are presented.
InChapter3,webrieflyexhibitthemathematicalformalismofQFT,which,as mentionedpreviously,hasanon-trivialcombinatorialbackbone.TheQFTsettingcan beunderstoodasaquantumdescriptionofparticlesandtheirinteractions,adescription whichisalsocompatiblewithEinstein’stheoryofspecialrelativity.Withintheframework ofelementaryparticlephysics(orhighenergyphysics),QFTledtotheStandard ModelofElementaryParticlePhysics,whichisthephysicaltheorytestedwiththebest accuracybycolliderexperiments.Moreover,theQFTformalismsuccessfullyapplies tostatisticalphysics,condensedmatterphysics,andsoon.Weshowinthischapter howFeynmangraphsappearthroughtheso-calledQFTperturbativeexpansion,how FeynmanintegralsareassociatedtoFeynmangraphs,andhowtheseintegralscanbe
expressedviathehelpofgraphpolynomials,theKirchhoff–Symanzikpolynomials. Finally,wegiveaglimpseofrenormalization,oftheDSE,andoftheuseofthesocalledintermediatefieldmethod.Thischaptermainlyfocusesontheso-called Φ4 QFT scalarmodel.
InChapter4,wedefinespecifictreeweightswhichappearnaturalwhenconsidering acertainapproachtonon-perturbativerenormalizationinQFT,namelyconstructiverenormalization.Severalexamplesofsuchtreeweightsareexplicitlygivenin AppendixA.
Chapter5dealswithacombinatorialQFTapproachtotheJacobianconjecture.The JacobianConjecturestatesthatanycomplex n-dimensionallocallyinvertiblepolynomial systemisgloballyinvertiblewithapolynomialinverse.In1982,Bassetal.proved animportantreductiontheoremstatingthattheconjectureistrueforanydegreeof thepolynomialsystemifitistrueindegreethree.Weshow,inthischapter,aresult concerningpartialeliminationofvariables,whichimpliesareductionofthegenericcase tothequadraticone.Thepricetopayistheintroductionofasupplementaryparameter, 0 ≤ n ≤ n parameter,whichrepresentsthedimensionofalinearsubspacewheresome particularconditionsonthesystemmusthold.Weexhibitaproof,inaQFTformulation, usingtheintermediatefieldmethodexposedinChapter3.
InChapter6,weuseGrassmanncalculus,usedinfermionicQFT,tofirstgivea reformulationoftheLingström–Gessel–Viennotlemmaproof.Wefurthershowthat thisproofgeneralizestographswithcycles.WethenusethesameGrassmanncalculus techniquestogivenewproofsofStembridge’sidentitiesrelatingappropriategraph Pfaffianstoasumovernon-intersectingpaths.Theresultspresentedheregofurther thantheonesofStembridge,becauseGrassmannalgebratechniquesnaturallyextend (withoutanycost!)tographswithcycles.Wethusobtain,insteadofsumsovernonintersectingpaths,sumsovernon-intersectingpathsandnon-intersectingcycles.In thefifthsectionofthechapter,wegiveageneralizationoftheseresults.Inthesixth sectionofthischapterweuseGrassmanncalculustoexhibittherelationshipbetweena multi-variateversionofTuttepolynomialandtheKirchhoff–Symanzikpolynomialsof theparametricrepresentationofFeynmanintegrals,polynomialsalreadyintroducedin Chapters1andresp.3.
InChapter7,wepresenthowseveralanalytictechniques,oftenusedincombinatorics, appearnaturallyinvariousQFTissues.Inthefirstsection,weshowhowonecanuse theMellintransformtechniquetore-expressFeynmanintegralsinausefulwayforthe mathematicalphysicist.Finally,webrieflypresenthowthesaddlepointapproximation techniquecanbealsousedinQFT.
InChapter8,afterabriefalgebraicreminder,weintroduceinthesecondsectionthe Connes–KreimerHopfalgebraofFeynmangraphsandweshowitsrelationshipwith thecombinatoricsofQFTperturbativerenormalization.Wethenstudythealgebra’s HochschildcohomologyinrelationwiththecombinatorialDSEinQFT.Inthefourth, sectionwepresentaHopfalgebraicdescriptionoftheso-calledmulti-scalerenormalization(themulti-scaleapproachtotheperturbativerenormalizationbeingthestarting pointfortheconstructiverenormalizationprogramme).
InChapter9,wepresentthe Phi4 QFTmodelonthenon-commutativeMoyal spaceandtheUV/IRmixingissue,whichpreventsitfrombeingrenormalizable.We thenpresenttheGrosse–Wulkenhaar Phi4 QFTmodelonthenon-commutativeMoyal space,whichchangestheusualpropagatorofthe Φ model(basedontheheatkernel formula)toaMehlerkernel-basedpropagator.ThisGrosse–Wulkenhaarmodelis perturbativelyrenormalizablebutitisnottranslation-invariant(translation-invariance beingausualpropertyofhigh-energyphysicsmodels).WethenshowhowtheMellin transformtechniquecanbeusedtoexpresstheFeynmanintegralsoftheGrosse–Wulkenhaarmodel.Inthelastpartofthechapter,wepresentanother Phi4 QFT modelonthenon-commutativeMoyalspace,whichishoweverbothrenormalizable andtranslation-invariant.Weshowtherelationbetweentheparametricrepresentation ofthismodelandtheBollobás–Riordanpolynomial.Finally,weshowhowtodefinea Connes–KreimerHopfalgebrafornon-commutativerenormalizationandhowtostudy itsHochschildcohomologyinrelationtothecombinatorialDSEoftheseQFTmodels.
Thelastpartofthebookisdedicatedtothestudyofcombinatorialaspectsof quantumgravitymodels.Thus,inChapter10,afterabriefintroductorysectionto quantumgravity,wementionthemaincandidatesforaquantumtheoryofgravity: stringtheory,loopquantumgravity,andgroupfieldtheory(GFT),causaldynamical triangulations,andmatrixmodels.ThenextsectionsintroducesomeGFTmodelssuch astheBoulatovmodel,thecolourable,andthemulti-orientablemodel.Thesaddlepoint methodforsomespecificGFTFeynmanintegralsispresentedinthefifthsection. Finally,somealgebraiccombinatoricsresultsarepresented:definitionofanappropriate Connes–KreimerHopfalgebradescribingthecombinatoricsoftherenormalizationof acertaintensorGFTmodel(theso-calledBenGeloun–Rivasseaumodel)andthe useofitsHochschildcohomologyforthestudyofthecombinatorialDSEofthis specificmodel.
InChapter11,afterabriefpresentationofrandommatricesasarandomsurfaceQFT approachto2Dquantumgravity,wefocusontwocrucialmathematicalphysicsresults: theimplementationofthelarge N limit(N beingherethesizeofthematrix)andofthe doublescalingmechanismformatrixmodels.Itisworthemphasizingthat,inthelarge N limit,itistheplanarsurfaceswhichdominate.Inthethirdsectionofthechapter,we introducetensormodels,seenasanaturalgeneralization,indimensionshigherthentwo, ofmatrixmodels.Thelastsectionofthechapterpresentsapotentialgeneralizationof theBollobás–Riordanpolynomialfortensorgraphs(whicharetheFeynmangraphsof theperturbativeexpansionofQFTtensormodels).
InChapter12,wefirstbrieflypresentthe U (N )D -invarianttensormodels(N being againthesizeofthetensor,and D beingthedimension).Thenextsectionisthen dedicatedtotheanalysisoftheDyson–Schwingerequations(DSEs)inthelargeN limit.Theseresultsareessentialtoimplementthedoublescalinglimitmechanismofthe DSEswhichisdoneinthethirdsection.Themainresultofthischapteristhedoublyscaledtwo-pointfunctionforamodelwithgenericmelonicinteractions.However,several assumptionsonthelarge N scalingofcumulantsaremadealongtheway.Theyare provedusingvariouscombinatorialmethods.
Chapter13isdedicatedtothepresentationofthemulti-orientabletensormodel.After definingthemodel,the 1/N expansionandthelarge N limitareexaminedinthesecond sectionofthechapter.Inthethirdsection,athoroughenumerativecombinatorialanalysis ofthegeneraltermofthe 1/N expansionispresented.Theimplementationofthedouble scalingmechanismisthenexhibitedinthefourthsection.
InChapter14,wedefineyetanotherclassoftensormodels,endowedwith O (N )3 invariance,Nbeingagainthesizeofthetensor.Thisallowstogenerate,via theusualQFTperturbativeexpansion,aclassofFeynmantensorgraphswhichis strictlylargerthantheclassofFeynmangraphsofboththemulti-orientablemodeland the U (N )3 -invariantmodelstreatedintheprevioustwochapters.Wefirstexhibitthe existenceofalargeNexpansionforsuchamodelwithgeneralinteractions(notnecessary quartic).Wethenfocusonthequarticmodelandweidentifytheleadingorder(LO) andnext-to-leading(NLO)Feynmangraphsofthelarge N expansion.Finally,weprove theexistenceofacriticalregimeandwecomputetheso-calledcriticalexponents.This isachievedthroughtheuseofvariousanalyticcombinatoricstechniques.
InChapter15,wefirstreviewtheSYKmodel,whichisaquantummechanical modelof N fermions.Themodelisaquenchedmodel,whichmeansthatthecoupling constantisarandomtensorwithGaussiandistribution.TheSYKmodelisdominated inthelargeNlimitbymelonicgraphs,inthesamewaythetensormodelspresented inthepreviousthreechaptersaredominatedbymelonicgraphs.Wethenpresenta purelygraphtheoreticalproofofthemelonicdominanceoftheSYKmodel.Asalready mentioned,itisthispropertywhichledE,wittentorelatetheSYKmodeltothecoloured tensormodel.Intherestofthechapterwedealwiththeso-calledcolouredSYKmodel, whichisaparticularcaseofthegeneralizationoftheSYKmodelintroducedbyD. GrossandV.Rosenhaus.WefirstanalyseindetailtheLOandNLOordervacuum,twoandfour-pointFeynmangraphsofthismodel.Wethenexhibitathoroughasymptotic combinatorialanalysisoftheFeynmangraphsatanarbitraryorderinthelarge N expansion.Weendthechapterbyananalysisoftheeffectofnon-Gaussiandistribution forthecouplingofthemodel.
InChapter16,weanalyseindetailthediagrammaticsofvariousSKY-liketensor models:theGurau–Wittenmodel(inthefirstsection),andthemulti-orientableand O (N )3 -invarianttensormodels,intherestofthechapter.Variousexplicitgraph theoreticaltechniquesareused.
2 Graphs,ribbongraphs, andpolynomials Inthischapter,wepresentsomenotionsofgraphtheorythatwillbeusefulinthe restofthisbook.Letusemphasizethatgraphtheoristsandquantumfieldtheorists adopt,unfortunately,differentterminologies.Wepresentbothhere,suchthatasortof dictionary betweenthesetwocommunitiesmaybeestablished.
Wethenextendthenotionofgraphstothatofmaps(orofribbongraphs).Moreover, graphpolynomialsencodingthesestructures(theTuttepolynomialforgraphsandthe Bollobás–Riordanpolynomialforribbongraphs)arepresented.
Inthischapter,wefollowtheoriginalarticle(ThomasKrajewskietal.2010)andthe reviewarticle(AdrianTanasa2012).
2.1Graphtheory:TheTuttepolynomial Forageneralintroductiontographtheory,theinterestedreadermayrefertoClaude Berge(1976).Letusnowdefineagraphinthefollowingway:
Definition2.1.1 Agraph Γ isdefinedasasetofvertices V andofedges E togetherwithan incidencerelationshipbetweenthem.
Noticethatweallowmulti-edgesandself-loops(seedefinition2.1.2 4),butstilluse theterm‘graph’(andnot‘pseudograph’).
Thenumberofverticesandedgesinagrapharealsonoted V and E forsimplicity, sinceourcontextpreventsconfusion.
OneneedstoemphasizethatinQFTasupplementarytypeofedgeexists, external edges.Theseedgesareonlyhookedtooneoftheverticesofthegraph,theotherend oftheedgebeing‘free’(seeFig.2.1foranexampleofsuchagraph,withfourexternal edges).Inelementaryparticlephysics,theseexternaledgesarerelatedtotheobservables insomeexperiments.
Graphs,ribbongraphs,andpolynomials
Figure2.1 A Φ4 graph,withfourinternaledgesandfourexternaledges
Letusnowgivethefollowingdefinition:
Definition2.1.2
1. Thenumberofedgesatavertexiscalledthe degree oftherespectivevertex(field theoristsrefertothisasthe coordinationnumber oftherespectivevertex).
2. Anedgewhoseremovalincreasesthenumberofconnectedcomponentsofthe respectivegraphiscalleda bridge (fieldtheoristsrefertothisasa 1-particle reducible edge).
3. Aconnectedsubsetofequalnumberofedgesandofverticeswhichcannotbe disconnectedbyremovinganyoftheedgesiscalleda cycle (fieldtheoristsrefer tothisasa loop).
4. Anedgewhichconnectsavertextoitselfiscalleda self-loop (fieldtheoristsreferto thisasa tadpole edge).
5. Anedgewhichisneitherabridgenoraself-loopiscalled regular
6. Anedgewhichisnotaself-loopiscalled semi-regular
7. Agraphwithnocyclesiscalleda forest.
8. Aconnectedforestiscalleda tree.
9. A two-tree isaspanningtreewithoutoneofitsedges.
10. The rank ofasubgraph A isdefinedas
where k (A) isthenumberofconnectedcomponentsofthesubgraph A.
11. The nullity (or cyclomaticnumber)ofasubgraph A isdefinedas
Remark2.1.3 Foraconnectedgraph,thenullitydefinedpreviouslyrepresentsthenumberof independentcircuits.
InQFT,oneoftenusestheterm(numberof)loopstodenote(thenumberof) independentloops.
Figure2.2 Anexampleofagraph(withsevenedgesandsixexternaledges).Wechoseaspanningtree andlabelleditsedgesby1,..., 4.Wethenchosetheedge3toberemoved.Theset{1,2,4}isatwo-tree; onehastwoconnectedcomponents(thefirstoneformedbytheedges1and2andthesecondoneformed byedge4).Theexternaledgesareattachedtooneofthesetwoconnectedcomponents
Remark2.1.4 Atwo-treegeneratestwoconnectedcomponentsontherespectivegraph.Letus alsonotethatatwo-treecanbedefinedasaspanningforestwithtwoconnectedcomponents(in thisway,norelationwithatreeisgiven).
LetusillustratethisinFig.2.2.Onecandefinetwonaturaloperationsforanarbitrary edge e ofsomegraph Γ:
1.thedeletion,whichleadstoagraphnoted Γ e;
2.thecontraction,whichleadstoagraphnoted Γ/e.Thisoperationidentifiesthe twovertices v1 and v2 attheendsof e intoanewvertex v12 ,attributingallthe edgesattachedto v1 and v2 to v12 ;finally,thecontractionoperationremoves e
Remark2.1.5 If e isaself-loop,then Γ/e isthesamegraphas Γ e.
Foranillustrationofthesetwooperations,onecanrefertoFig.2.3,wherethese operationsareiterateduntilonereaches terminalforms namelygraphsformedonly ofself-loopsandbridges.
LetusnowgiveafirstdefinitionoftheTuttepolynomial:
Definition2.1.6 If Γ isagraph,thenitsTuttepolynomial TΓ (x,y ) isdefinedas
AfundamentalpropertyoftheTuttepolynomialisadeletion/contractionproperty:
Graphs,ribbongraphs,andpolynomials
Figure2.3 Thedeletion/contractionofsomegraph.Oneisleftwithvariouspossibilities(herefive)of terminalforms(thatis,graphswithonlybridgesorself-loops)
Theorem2.1.7 If Γ isagraph,and e isaregularedge,then
ThispropertyoftheTuttepolynomialisoftenusedasitsdefinition,ifonecompletes itbygivingtheformoftheTuttepolynomialonterminalforms:
where m isthenumberofbridgesand n isthenumberofself-loops.
Multi-variate(orweighted)versionsoftheTuttepolynomialexistintheliterature. Thus,intheseminalpaper,AlanD.Sokal(2005)analysedindetailsuchamulti-variate polynomial.Themainideaisthefollowing:oneintroducesasetofvariables β1 ,...,βE , oneforeachedge,andavariable q ,insteadofthecoupleofvariables x and y oftheTutte polynomial.
Othermulti-variateversionscanalsobefoundintheliteraturebuttheyareessentially equivalenttotheSokalpolynomialafterappropriatechangesofvariables.Nevertheless, thisisnotthecaseforthepolynomialsdefinedinZaslavsky(1992)andBollobásand Riordan(1992)(seealsoEllis-MonaghanandTraldi(2006)forgeneralizations).
Letusgivethedefinitionofthefollowingmulti-variateversionoftheTutte polynomial:
Graphtheory:TheTuttepolynomial 11
Definition2.1.8 If Γ isagraph,thenitsmulti-variateTuttepolynomialisdefinedas
Similarly,onecanprovethatthemulti-variateTuttepolynomial (2.6) satisfiesthe deletion/contractionrelation,foranyedge e.Thedefinitionofthepolynomialonthe terminalforms(graphswith v isolatedvertices)is
Onecanprove(throughdirectinspection)therelationbetweentheTuttepolynomial (2.3) anditsmulti-variatecounterpart (2.6):
Itisthisversionofthemulti-variateTuttepolynomial (2.6) thatweuseinthisbookto provetherelationwiththeparametricrepresentationofFeynmanintegralsinQFT(see Chapter6.6).
PuttingasidetheTuttepolynomial,severalgraphpolynomialshavebeendefinedand extensivelystudiedintheliterature.Aswehaveseenpreviously,theTuttepolynomial isatwo-variablepolynomial.Ithasone-variablespecializations,suchasthechromatic polynomialortheflowpolynomial.
The chromaticpolynomial isagraphpolynomial PΓ (k ) (k ∈ N )whichcountsthe numberofdistinctwaystocolourthegraph Γ with k orfewercolours,colouringsbeing countedasdistincteveniftheydifferonlybypermutationofcolours.Foraconnected graph,thispolynomialisrelatedtotheTuttepolynomial (2.3) bytherelation
Inordertodefinetheflowpolynomial,weneedafiniteabeliangroup G.One canarbitrarilychooseanorientationforeachedgeofthegraph Γ,theresultbeing independentofthischoice(thesametypeofsituationappearswhencomputingFeynman integrals,seenextsection).A G flow on Γ isamapping
thatsatisfiescurrentconservationateachvertex.A G flowon Γ issaidtobe nowherezero if ψ (e) =0 forall e.Let FΓ (G) bethenumberofnowhere-zero G flowson Γ.One canprovethatthisnumberdependsonlyontheorder k ofthegroup G;itcanthusbe written FΓ (k )—itistherestrictiontonon-negativeintegersofapolynomialin k ,the flow polynomial
Graphs,ribbongraphs,andpolynomials
Onehas:
AcrucialpropertyoftheTuttepolynomialisitspropertyof universality.This propertystatesthatanyTutteinvariant(i.e.anygraphpolynomialsatisfyingdeletion/contractionpropertyandamultiplicativelawongraphdisjointreunionandonevertexjoint)isanevaluationoftheTuttepolynomial.Thispropertyisprovedinthe combinatoricsliteraturebycarefullyusinginductionargumentsontheedgesofthe graph.
LetusendthissectionbyemphasizingthattheTuttepolynomial(anditsmulti-variate versionthatwehavepresentedhere)extendsinanaturalmannertothemoreinvolved combinatorialnotionof matroids (seeagainSokal(2005)).
2.2Ribbongraphs;theBollobás–Riordanpolynomial Inthissection,weintroduceanaturalgeneralizationofthenotionofgraphs—ribbon graphsormaps.Forageneralintroductiontocombinatorialmaps,theinterestedreader mayrefertoGuillaumeChapuy’sPhDthesisChapuy(2009)ortoGillesSchaeffer’suse (2009).
Letusdefinesucharibbongraphinthefollowingway:
Definition2.2.1 A ribbongraph Γ isanorientablesurfacewithitsboundaryrepresented astheunionofcloseddisks,alsocalled vertices,andribbonsalsocalled edges,suchthat: thedisksandribbonsintersectindisjointlinesegments,eachsuchlinesegmentlyingonthe boundaryofpreciselyonediskandoneribbonandfinally,everyribboncontainingtwosuch linesegments.
Notethat,asinthecaseofgraphs,thisdefinitioncanbeextendedbyaddinganew typeofedge(notwithtwolinesegments,seethepreviousdefinition)suchthat external edges areallowed(seeprevioussubsection).Examplesofsuchgraphsaregivenin Figs.2.4and2.5.
Letusalsomentionthatribbongraphscanbedefinedasgraphsequippedwitha cyclicorderingoftheincidenceedgesateachvertexorasgraphsembeddedinsurfaces (thelatterwasactuallythemathematicalobjectonwhichB.BollobásandO.Riordan definedtheirgeneralizationoftheTuttepolynomialinBollobásandRiordan(2001)and BollobásandRiordan(2002),seefollowingsection).
Aninteresting connectionbetweentheTuttepolynomialofgraphsandcombinatorialmaps wasproveninBernardi(2008).HegaveacharacterizationoftheTuttepolynomialof graphswhichisdifferenttotheinitialonegivenbyTutte(whichrequiredsomechoice oflinearorderontheedgeset,inordertowritetheTuttepolynomialasafunctionof
Ribbongraphs;theBollobás–Riordanpolynomial
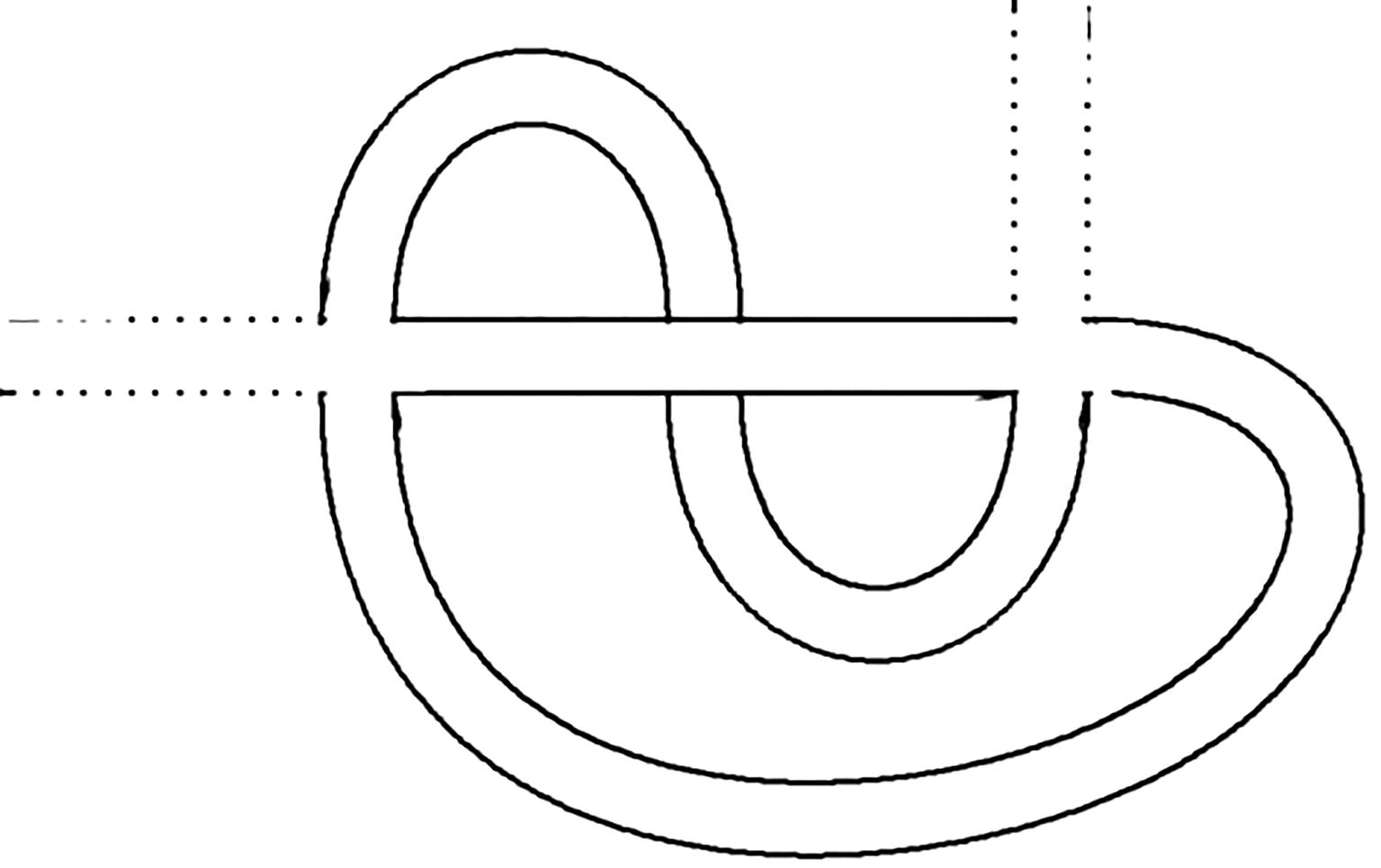
Figure2.4 Anexampleofaribbongraphwithonevertex,oneinternaledge,andtwoexternaledges
Figure2.5 Anexampleofaribbongraphwithtwovertices,threeinternaledges,andtwoexternaledges spanningtrees).O.BernardiprovedthattheTuttepolynomialcanalsobewrittenasthe generatingfunctionofspanningtreescountedwiththehelpofacyclicorderoftheedges aroundeachvertex.
Letusnowgivethefollowingdefinition:
Definition2.2.2 A face ofaribbongraphisaconnectedcomponentofitsboundaryasa surface.
Forexample,thegraphofFig.2.4hastwofaces,whiletheoneofFig.2.5hasasingle face.IfwegluedisksalongthefacesweobtainaclosedRiemannsurfacewhosegenusis alsocalledthe genus ofthegraph.
Definition2.2.3 Theribbongraphiscalled planar ifithasvanishinggenus.
Forexample,thegraphofFig.2.4isplanarwhiletheoneofFig.2.5isnon-planar(it hasgenus 1).