https://ebookmass.com/product/bands-and-photons-in-iii-vsemiconductor-quantum-structures-igor-vurgaftman/
Instant digital products (PDF, ePub, MOBI) ready for you
Download now and discover formats that fit your needs...
Quantum Physics of Semiconductor Materials and Devices
Debdeep Jena
https://ebookmass.com/product/quantum-physics-of-semiconductormaterials-and-devices-debdeep-jena/
ebookmass.com
Underwater Inspection and Repair for Offshore Structures
John V. Sharp
https://ebookmass.com/product/underwater-inspection-and-repair-foroffshore-structures-john-v-sharp/
ebookmass.com
Quantum Communication, Quantum Networks, and Quantum
Sensing Ivan Djordjevic
https://ebookmass.com/product/quantum-communication-quantum-networksand-quantum-sensing-ivan-djordjevic/ ebookmass.com
Economics and Ageing : Volume III: Long-term Care and Finance 1st ed. 2020 Edition José Luis Iparraguirre
https://ebookmass.com/product/economics-and-ageing-volume-iii-longterm-care-and-finance-1st-ed-2020-edition-jose-luis-iparraguirre/ ebookmass.com
A Play for Love (The Scottish Billionaires Book 11) M. S. Parker https://ebookmass.com/product/a-play-for-love-the-scottishbillionaires-book-11-m-s-parker/
ebookmass.com
SMOKY ESCAPE: Knoxville FBI - Book Three Liz Bradford
https://ebookmass.com/product/smoky-escape-knoxville-fbi-book-threeliz-bradford/
ebookmass.com
Travel Writings on Asia: Curiosity, Identities, and Knowledge Across the East, c. 1200 to the Present Christian Mueller
https://ebookmass.com/product/travel-writings-on-asia-curiosityidentities-and-knowledge-across-the-east-c-1200-to-the-presentchristian-mueller/
ebookmass.com
Auctioned to the Stranger : Protective Alpha Hero (Highest Bidder Club Book 3) Cassi Hart
https://ebookmass.com/product/auctioned-to-the-stranger-protectivealpha-hero-highest-bidder-club-book-3-cassi-hart/
ebookmass.com
John Cheever - Toplu Öyküler 1st Edition John Cheever
https://ebookmass.com/product/john-cheever-toplu-oykuler-1st-editionjohn-cheever/
ebookmass.com
https://ebookmass.com/product/remix-3rd-edition-ebook-pdf/
ebookmass.com
SERIESONSEMICONDUCTOR SCIENCEANDTECHNOLOGY
SeriesEditors
R.J.NicholasUniversityofOxford
H.KamimuraUniversityofTokyo
SERIESONSEMICONDUCTORSCIENCEANDTECHNOLOGY
1.M.Jaros: Physicsandapplicationsofsemiconductormicrostructures
2.V.N.DobrovolskyandV.G.Litovchenko: Surfaceelectronictransportphenomenainsemiconductors
3.M.J.Kelly: Low-dimensionalsemiconductors
4.P.K.Basu: Theoryofopticalprocessesinsemiconductors
5.N.Balkan: Hotelectronsinsemiconductors
6.B.Gil: GroupIIInitridesemiconductorcompounds:physicsandapplications
7.M.Sugawara: Plasmaetching
8.M.Balkanski,R.F.Wallis: Semiconductorphysicsandapplications
9.B.Gil: Low-dimensionalnitridesemiconductors
10.L.Challis: Electron-phononinteractionsinlow-dimensionalstructures
11.V.Ustinov,A.Zhukov,A.Egorov,N.Maleev: Quantumdotlasers
12.H.Spieler: Semiconductordetectorsystems
13.S.Maekawa: Conceptsinspinelectronics
14.S.D.Ganichev,W.Prettl: Intenseterahertzexcitationofsemiconductors
15.N.Miura: Physicsofsemiconductorsinhighmagneticfields
16.A.V.Kavokin,J.J.Baumberg,G.Malpuech,F.P.Laussy: Microcavities
17.S.Maekawa,S.O.Valenzuela,E.Saitoh,T.Kimura: Spincurrent
18.B.Gil: III-nitridesemiconductorsandtheirmoderndevices
19.A.Toropov,T.Shubina: PlasmonicEffectsinMetal-Semiconductor Nanostructures
20.B.K.Ridley: HybridPhononsinNanostructures
21.A.V.Kavokin,J.J.Baumberg,G.Malpuech,F.P.Laussy: Microcavities,Second edition
22.S.Maekawa,S.O.Valenzuela,E.Saitoh,T.Kimura: Spincurrent,Second Edition
23.M.M.Glazov: Electronandnuclearspindynamicsinsemiconductor nanostructures
24.D.Meier,J.Seidel,M.Gregg,R.Ramesh: Domainwalls:fromfundamental propertiestonanotechnologyconcepts
25.I.Vurgaftman,M.Lumb,J.Meyer: BandsandphotonsinIII-Vsemiconductor quantumstructures
BandsandPhotonsinIII–V SemiconductorQuantumStructures IgorVurgaftman,MatthewP.Lumb,andJerryR.Meyer
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries
©Vurgaftman,Lumb,andMeyer2021
Themoralrightsoftheauthorshavebeenasserted FirstEditionpublishedin2021 Impression:1
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica
BritishLibraryCataloguinginPublicationData
Dataavailable
LibraryofCongressControlNumber:2020944521
ISBN978–0–19–876727–5
DOI:10.1093/oso/9780198767275.001.0001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
InscriptiononaRomanvase
ILLVMINAT·OMNEM·STRVCTVRAM·BANDVM
Preface Whydoweneedyetanotherbookonthephysicsofsemiconductorquantum structuresandphotonicdevices?Thewritingprocesshastakenenoughtimefrom ourregularlives(andthepurchasemaytakeenoughfromapotentialreader’s wallet)thatwecannotbrushthisquestionasidelightly.
First,wefeelthattheexistingtreatmentsfallalittleshortofpresentingthe theoryofbandstructureandopticalpropertiesinafullylogicalandself-contained manner.Aswetrytoshowinthisbook,thistheoryissurprisinglyaccessibleata ratherdeeplevelanddoesnotdemandmuchbackgroundfromthereader,apart fromabasicgroundinginquantummechanicsandelectromagnetism.Insome cases,wefindthatothersourcesdonotmakeitclearhow minimal amodelcanbe andstillremainadequateforaparticularclassofdevices.
Second,wewouldliketoexpandandbringuptodatesomeofthecontent thatcanbefoundelsewhere.Weincludeextendeddiscussionsofquantumand interbandcascadelasers,superlatticephotodetectors,andnovelphotovoltaic conceptsaswellasamuch-neededupdateofthecomprehensivesetofband parametersfirstreportedina2001reviewbytwoofthepresentauthors(expanded andcorrectedin2003and2007forthewurtzites).
Third,thebooktriestoshedarayortwooflightonmanyconnectionsbetween thephysicsofIII–Vsemiconductorsandnewermaterialssuchasgrapheneand transitionmetaldichalcogenides.Today’sjuniorresearchersmaybenefitfrom followingtheselinks,sketchedinoutline,asthefieldinevitablypivotstothenext greatthing.
Howdidwedecidewhichtopicsshouldreceivethemostcare?Everyonetriesto tellthestorytheyknowbest,andwearenoexception.Thebookreliesonheavily onourpublishedwork,andhenceemphasizesmid-infrareddevices.Butthisis hardlyacompilation,andmuchofthematerialappearsintheformadoptedhere forthefirsttime.Wealsotrytotakeadvantageoftheextendedbookformatto provideamoregranularpictureandframeitinaslightlydifferentwaythatis fullyunderstandabletoourselves and,wehope,toanyothersufficientlymotivated readerwillingtogoalongfortheride.Sometimesthatrequiresdroppingrigorand bridgingthegapswithdimensionalandplausibilityarguments.Atothertimes,we usequantitativeexamplestomakethemagnitudeoftheeffectclear.
Hereisabriefoverviewoftheactualcontentofthebook.PartIlaysthefoundationforPartsII,III,andIVindescribinghowthemostimportantregionsofthe bandstructureclosetotheenergygapcanbemodeledusingapproachesthatrange fromquitesimpletoratherinvolved.Thebandstructuretechniqueofchoiceisthe 8-band k p methodanditsvarioussimplifiedforms,althoughwedonotneglect tight-bindingapproaches,includingtheeffectivebond-orbitalmethod,andthe empiricalpseudopotentialmethod.Chapter4discussestheopticalpropertiesof
bulkIII–Vsemiconductors,startingfromthebasicconceptsandculminatingin quantitativeanalysesoftheabsorption,gain,andradiativeemissioninbulkIII–V materials.PartIIpresentsacomprehensivetabulatedupdateoftherecommended bandparameters(hereaugmentedtoincludedilutebismides,boronnitride,and theopticalconstants)thatwerefirstpublishedbytwoofusnearlytwentyyears ago.Theseparametersareusedinthemodelsandsimulationresultspresentedin PartsI,III,andIV,andmayofcoursebeusedforgeneralreferenceinthereader’s ownbandstructureanddevicemodelingcalculations.PartIIIguidesthereader intothequantumrealm,anditsimplementationinsemiconductorepitaxiallayers withatomic-scalethicknesses.Itprovidestoolsforcomputingthebandstructures andopticalpropertiesofquantumwellsandsuperlattices,aswellasquantum wiresanddotswithmultidimensionalconfinement.Chapter11discussesthe opticalpropertiesofquantumheterostructures,focusingonabsorption,gain,and radiativeemissionprocessesthatmayresultfrombothinterbandandintersubband interactions.Finally,PartIVdescribesthephysicalprinciplesbehindphotonic devicesbasedonlayeredIII–Vsemiconductorsandhowtheyaredesignedusing thetoolsdevelopedinPartsIandIII.Lasers,photodetectors,solarcells,and nonlineardeviceswillbediscussed,withparticularemphasisonmid-infrared lasersandmid-waveandlong-wavesuperlattice-basedphotodetectors.Sinceallof thesedevicesrelyonnon-equilibriumfreecarriers,thevariousradiativeandnonradiativerecombinationprocessesthatcandominateunderdifferentconditions willbedescribed.
Everyonedislikesalongandramblingpreface.Ifthereaderindulgesusfor anotherparagraph,wewouldliketoreiteratethephilosophythathasguidedthe writingofthisbook.Whileitcomestoyouuntestedinaclassroom,wedohave vividmemoriesaswellasrecentexperiencesoflearningnewconcepts.Whenever anechoofthefamiliarresoundsinanexoticthicket,wefeelastepclosertothe destination.Forthisreason,weavoidpluckinga non-obvious mathematicalresult fromanotherreferenceandsendingthereaderscurryingofftocheckitsvalidity (andsometimesdespairingofeverdoingso!).Instead,weattempttomakeevery calculationasself-containedaspossibleinabookofthissize.Whenthatstretches thebook’sscopetoofar,weoutlinewhythegivenfactisplausibleandhowit connectstotheaccumulatedbodyofphysicalknowledge.Prizingintelligibility overcleverness,westeerclearofthemoreobscuretheoreticaltools,particularly wheretheyarenotstrictlynecessarytounderstandthematerial.Wealsotry topaintacontinuousnarrativeratherthanserveupafarragoofformulasand calculations.Havinggivenuponcitingeveryrelevantpaperunderthesun,we limitourreferencestoashortlistofthosearticlesandbooksthathavebeenthe mostusefultous.Theexceptionistheband-parameterupdateinPartII,whichis morecatholicandbuildsonourearlierreviews.Finally,wehaveaimedtokeepthe languagesimpleanddirect,notpepperedwithacronyms.Thereaderscanjudge forthemselvesthesuccess(orlackthereof!)inachievingthesegoalsfromthetext thatfollows.
Acknowledgments Weareimmenselygratefultothemanypeoplewhohaveworkedwithusoradvised usonthetopicscoveredhereoverthepastseveraldecades.Theseinclude,first andforemost,themembersofourresearchgroups,aswellasmanyworld-class scientists,someofwhoseinsightsfoundtheirwayintothebook.Whileweare unabletolisteveryonewhoshouldshareatleastsomecredit,specialthanksgo toBillBewley,ChadwickCanedy,ChulSooKim,MijinKim,CharlesMerritt, StephanieTomasulo,JacobKhurgin,EdwardAifer,L.R.Ram-Mohan,Jasprit Singh,andMariaGonzalez.Onamoreartisticfront,ChulSooKimdesigned thecoverimage,andYelenaVurgaftmanhelpedtodrawtheschematics.Itgoes withoutsayingthattheresponsibilityforanyerrorsrestswithusalone.
WearegratefultoSonkeAdlungandOxfordUniversityPressfortheirinterest intheinitialidea(thatdidnotflagasdeadlinespassed andpassed),andfor helpingtomakethepublicationprocesssmootherthanwecouldeverimagine. Finally,awordofthankstoourfamilieswhohavemadethisbookandmanyother thingspossible.
BasicsofCrystalStructure andBandStructure III–Vsemiconductorsformcrystallinestructureswiththree-dimensionalperiodic arrangementsoftheatoms.Inthischapter,wewillexplorethenatureofthecrystal latticestartingfromlowerdimensionsandprogressingtorealsemiconductor crystals.Wealsolearnwhyweexpectdistinctenergybandstoforminthesolids thatcrystallizeinsuchlattices.Thecarrierstatisticsandoccupationofthebands willalsobeexamined.
1.11Dand2DCrystals Inonedimension,movementisalongasingleline.Therefore,allperiodic1D structuresarealikeandcharacterizeduniquelybythelatticespacing a.Wecanalso placemorethanoneatomaroundeachperiodiclatticepoint,aconceptknownas addinga basis tothelattice.Ifthelatticeisdefinedbypointswithcoordinates na, where n isaninteger,onepossiblebasisistoputtwoatomsatrelativedistances ±b fromeachlatticepoint,sothattheatomicpositionsare na ± b,asshownin Fig.1.1.When b = a/2,thelatticewithatwo-atombasisdegeneratesintoasingleatombasiswithhalfthespacing,unlessofcoursethetwoatomsaredifferent.This isallweneedtoknowaboutone-dimensionalcrystalstructures.
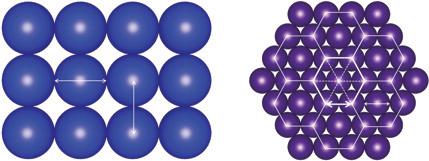
Addinganotherdimensionchangeseverything.Wecanconstructthe2Dlattice bytilingtheplanewitharepeatedunitcellandplacingtheatomssomewhere withineachcell.Therearefivedistinctarrangementsofthelatticepoints,andthe oneswiththehighestsymmetrytiletheplanewithsquaresorequilateraltriangles (or,equivalently,regularhexagons).
Symmetryispleasingtotheeye,butwhichofthepossibilitiesarethemost physicallyimportant?Therealanswerwillhavetowait,butwecanstartwitha guessthattheenergyisataminimumwhentheatomsarepackedintothesmallest possiblevolume.Toestimatethepackingdensityofeachcrystalstructure,we assumethatalltheatomsarecircular.
BandsandPhotonsinIII–VSemiconductorQuantumStructures.Vurgaftman,Lumb,andMeyer, OxfordUniversityPress(2021).©Vurgaftman,Lumb,andMeyer. DOI:10.1093/oso/9780198767275.003.0001
Figure1.1 One-dimensionalcrystallatticewithperiodaandabasisoftwoatomspositioned atrelativedistances ±bfromeachlatticepoint.
Forexample,thecirclesinthesquarelatticeillustratedinFig.1.2ajusttouch whentheirdiametersareequaltothelatticeperiod a.Sinceonlyonecirclefits withineachsquaretile,thefractionoftheplanecoveredbycirclesis
= areaofcircle
Canwedobetter?Clearly,arectangularlatticeisapoorchoicesincethecircles wouldtouchonlyalongtheshorterside.Thenwhataboutthetriangular(or hexagonal)latticeshowninFig.1.2b?Someofthecirclesaresharedbetween adjacenthexagonaltiles,sowecountonlythefractionofeachcirclethatfalls withinagivenhexagon.Inthiscase,onecircleliesentirelywithineachhexagon, andsixmorearesharedequallybetweenthreecells.Countingthesharedcircles as1/3each,weobtainatotalofthreecirclescontainedwithineachunitcell.The packingratioisthen
Fhex = 3 × (areaofcircle) areaofhexagon = 3π a2 /4 3√3a2 /2 = π 2√3
Thisisimpressivelyhigh,butcanweraiseitevencloserto1?Theanswerisno. Infact,wehaverunoutofbasicsymmetriestoconsider.Theplanecannotbe tiledbyregularoctagons,dodecagons,etc.,becauseanintegernumberofinternal angles, (k 2) π/k each,where k isthenumberofvertices,doesnotfitintoa
Figure1.2 (a)Square-latticearrangementofcircles,eachwithdiametera.(b)Hexagonal-lattice arrangementofcircleswithdiametera.
2π angleateachvertexwhen k > 6.Infact,theso-called Thue’stheorem states thatamongallpossibleperiodic and aperiodicarrangements,ahexagonallattice providesthehighestplanarfillingfractionforcirclesoffixedradius.
Wecanaddabasistothe2Dhexagonallatticetorepresenttwotypesofatoms inacompound.Theconceptwillalsocomeinhandywhentheatomsthemselves areidentical,buttheouter-shellelectronicconfigurationhasfewerthansixnearest neighbors.
Ingeneral,weneedtwointegers (m, n) todescribethepositionofeachatom. TheCartesiancoordinatesoftheatom (x, y) areequalto (m, n) multipliedbythe twolatticevectors.Forexample,ifwechoose
thesixnearestneighborsinahexagonallatticeare (m, n) = (±1,0) , (0, ±1) , (1, 1) and ( 1,1).Todefinethebasiswesuperposetwosuchlattices,withthesecond displacedby (0, b) relativetothefirstinCartesiancoordinates.If b = a/√3,this isthe“honeycomb”crystalstructureillustratedinFig.1.3,inwhicheachatom hasthreenearestneighborsthatoccupysitesontheothersublattice.Thedistance tothesixnearestneighborsonthesamesublatticeislargerbyafactorof √3.In Cartesiancoordinates,thepositionsofthenearestneighborswithrespecttoan atomattheoriginare
Theatomsinthetwointerpenetratingsublatticesmayormaynotbeidentical. III–Vsemiconductorsdonotproduceanytwo-dimensionalcrystals,butgroupIV elementspotentiallycan.Inparticular, graphene isa2Dhoneycombcrystalof carbonatoms.Wecanalsoconceiveof silicene, germanene,etc.Thethreenearest
Figure1.3 Twointerpenetratinghexagonallatticesthatproduceahoneycombcrystalstructure.
Table1.1 The2Dlatticestructuresdiscussedinthetext.
LatticeTypeFirstLatticeVectorSecondLatticeVector Square
(1,0)
Rectangular
(0,1)
(1,0)
)
Note:Thehoneycombpatternisahexagonallatticewiththetwo-atombasisdescribedby Eq.(1.4).
neighborsareaccommodatedby sp2 hybridizationoftheouter-shellelectrons, withthenon-hybridizedorbitalsformingtwoout-of-plane π bonds.Graphene becomesthethree-dimensionalgraphitecrystalwhenatomicplanesconfiguredin thehoneycomblatticearestackedverticallyandweaklybondedbyvanderWaals forces.Theimportant2DlatticestructuresaresummarizedinTable1.1,along withtheunitlatticevectors.
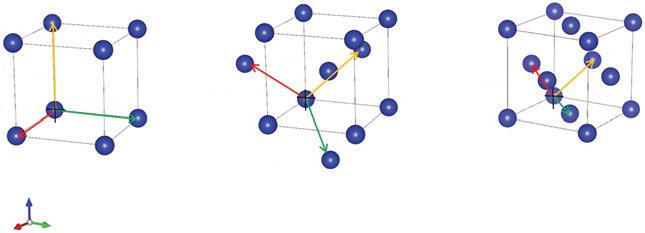
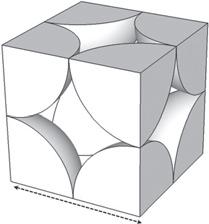
1.23DCrystalStructure Takingourcuefrom2Dcrystals,wenextcalculatehowdenselytheatoms— nowrepresentedbyspheres—canbepackedinthreedimensions.Thesimplest arrangementbyfaristhecubiclatticeshowninFig.1.4a,inwhichtheatoms occupytheverticesofacubewithside a.Anygivenvertexhassixnearest neighbors,separatedfromtheoriginby a.Forexample,theatomat (0,0,0) has nearestneighborsat (±1,0,0), (0, ±1,0),and (0,0, ±1).Thenumberofnearest neighborsinalatticeisreferredtoasthe coordinationnumber.Asinglespherewith diameter a fitsintothecubewithapackingfraction
Fcube = volumeofsphere volumeofcube = 4π (a/2)3 /3 a3 = π 6 ≈ 0.524(1.5)
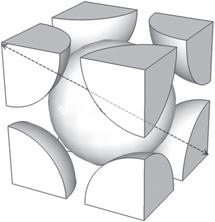
Surelywecandobetter!Whatifweplaceasingleatomatthecenterofthecube [(x, y, z) = a 1 2 , 1 2 , 1 2 ]andpositiontheothersattheverticesasshowninFig.1.4b? Thisarrangementisknownas body-centeredcubic (bcc).Ifthesphereatthecenter justtouchesthecornerspheres,thediagonalofthecube(withlength √3a)spans twospherediameters.Thereareeightspheresinthecorners,eachsharedbetween eightadjacentcells.Countingthesphereatthecenter,thismeansthateachcubic cellenclosestwospheresofdiameter √3a/2.Thepackingfractionisthen
Fbcc = 2 × (volumeofsphere) volumeofcube = 2 × 4π √3a/4 3 /3 a3 = √3π 8 ≈ 0.680(1.6)
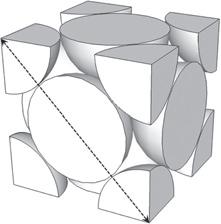
Figure1.4 (a)Cubiclattice,thesimplest3Darrangement,hasatomspositionedatthevertices ofacubewithsidelengtha.(b)Body-centeredcubiclattice,whichplacesasingleatominthe centerofthecubeandothersateachvertex.Alsoshownisthemostconvenientsetoflattice vectors,whicharedrawnfromacorneratomtothecenteratominthenextcell.(c)Face-centered cubiclattice,whichpositionsadditionalatomsatthecenterofeachfaceofthecube.Alsoshownis aconvenientsetoflatticevectorsthatconnectsacorneratomtotheatomsonthreeadjacentfaces. Theschematicbeloweachlatticediagramillustratesthespacefillingbyspherescenteredatthe latticesites.Inthecubiclatticeasinglesphereofdiameterd = afitsintothecube,inthebcc latticetwospheresofdiameterd = √3a/2 fitintoabodydiagonal,andinthefcclatticetwo spheresofdiameterd = √2a/2 fitintoafacediagonal.
Naïvethoughourpackingargumentmaybe,thebcclatticedoesoccurinnature asthecrystalstructureofafewelementarysolids.
Wecandefinethebcclatticevectorsinanumberofways.Themostconvenient choiceistodrawthevectorsfromacorneratominonecellsymmetricallytothe centeratomsintheneighboringcells:
Theatomatthecubecenterisclosertothoseattheverticesofthesamecube (adistanceof √3a/2)thanitistoatomsatthecentersoftheneighboringcubes (adistanceof a).Therefore,thecoordinationnumberforthebcclatticeiseight.
Ifdenserpackinggoestogetherwiththehighercoordinationnumber,canwe findalatticewithacoordinationnumbergreaterthaneight?Tryaddingmore atomstothecubeinthemostsymmetricalwaypossible!Wecandothisbyputting theextraatomsatthecentersofthesixfacesratherthanatthecenterofthecube. This face-centeredcubic (fcc)lattice,illustratedinFig.1.4c,looksthesamefrom anygivenpointinanydirection.Ithasahighercoordinationnumberthanthe bcclattice,becausethenearestneighborsoftheatomat (0,0,0) areatthecenters ofthe12adjacentfaces a (±1, ±1,0), a (0, ±1, ±1),and a (±1,0, ±1) locatedon thethreeintersectingplanes.Wechoosethefollowingsymmetriclatticevectorsto describethefcclattice:
Doesthehighercoordinationnumberforthefcclatticegiveahigherpacking fraction?Inthefcclattice,theatomsatthecentersofthesixfacesarehalfinside thecubepicturedinFig.1.4c,whilethoseattheeightverticesareonly1/8within thatcube.Thisaddsuptofoursphericalvolumesinsidethecube.Sincewecan fittwodiametersintoafacediagonalwithlength √2a,thepackingfractionis
= 4 × (volumeofsphere
Thefractionisindeedhigher,butonlyby < 10percentcomparedtoEq.(1.6), eventhoughthecoordinationnumberisupby50percent.Thisshouldalertusthat weareapproachinganupperlimit.Italsomakesintuitivesensethatextraopen spaceisunavoidablewhenatomsarepackedin3Dratherthan2D.Arethereany otherlatticeconfigurationswehavemissed?Forexample,couldwehaveacubic latticewithadditionalatomsatthecentersoftheedgesratherthanonthefaces? No,this“edge-centeredlattice”isnotinfactavalidlattice,becausewithgaping holesatthecubecentersandsixfacesitdoesnotlookthesamefromalldirections. Ofcourse,ifthesegapsarefilledwithatoms,werecoverasimplecubiclatticewith halftheperiod.Weconcludethatthepotentialforimprovementwithinthecubic geometryisatanebb.
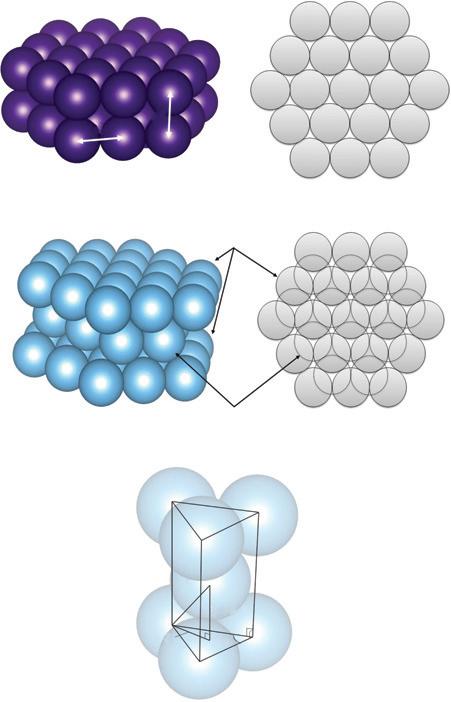
InSection1.1,ahexagonalgeometrygavethetightestfitin2D.Mightweusea similartypeofpackingin3D?Wecansimplyborrowthefirsttwolatticevectors fromthe2DforminEq.(1.3)andchoosethethirdtopointalongthe z axiswith somelength c.Now,whatvalueof c (inunitsof a)yieldsthedensestpacking arrangement?Westartwithalltheatomsinsuccessivehexagonalplaneslying exactlyontopofoneanother,asillustratedinFig.1.5a.Here c issimplyequalto a.Asintheanalogous2Dcase,therearethreeatomsperunitcellsinceexactly halfofeachlayerfitsinside.Thelatticevectorsare
ThelatticevectorsinEq.(1.10)applytoanyhexagonalgeometrywith c = a aswellas c = a
Thecellvolumeistheareaofthehexagontimes
= 3√3a3 /2.Thepackingfractionisthen
Thisisnobetterthanthefcclattice,butwhatifweslidetheupperlayersothatit fitsintotheinterstitialsbetweentheatomsofthefirstlayer,asshowninFig.1.5b?
Thethirdlayerisalignedwiththefirst,thefourthwiththesecondetc.,asifwewere stackingcannonballs(ororanges).Theunitcell,whichconsistsofboththefirst andsecondlayers,nowhasthreeextraatoms,foratotalofsix.Thecellvolumeis againtheproductofthehexagon’sareaand c,whichwewouldliketocalculatein termsof a
Thedistancebetweenthefirstandsecondlayersissimply c/2inthisgeometry. Thedistancebetweenagivenatomandthenearestatomsinthenextlayeris a, sothatthetwospheresofdiameter a arejusttouching.Thisisthehypotenuse oftherighttriangleshowninFig.1.5c.Thelegintheplaneisequaltothe distancebetweenonevertexandthecenterofanequilateraltriangleformedby theneighboringvertices,i.e.,halfthesidelengthdividedbythecosineofthe half-angle, a/ 2 cos 30 ◦ = a/√3.ApplyingthePythagoreantheoremtotheright triangleinFig.1.5c,weobtain
andthepackingfractionbecomes
Thepackingfractionof74.0percentforthisaptlynamed hexagonalclosepacked(hcp) latticeisthesameasforthefcclattice!Wehaveindeedreacheda
b)
(2/3) a a/√3 a a a 60° a a
c=2√(2/3) a
Figure1.5 (a)Projectionandplanviewofa3Dhexagonallatticeinwhicheachhexagonal layerliesexactlyontopoftheonebelowit(c = a);(b)3Dprojectionandplanviewofthe hexagonalclose-packed(hcp)lattice,inwhichtheatomsofsublatticeBfitinterstitiallybetween theatomsofsublatticeA;(c)out-of-planelatticeconstantcforthehcplattice,asfoundby applyingthePythagoreantheoremtotherighttrianglecomposedofthevertexinthefirstlayer,a vertexinthesecondlayer,andthecenteroftheequilateraltrianglejustbelowthesecond-layer vertex.
fundamentallimit,andinfact,thereisasurprisinglycloseconnectionbetween thefccandhcplattices.Whenviewedalongthe[111]direction,thefcclattice looksverymuchlikethehcplatticeexceptthethirdlayerisplacedindifferent interstitialsofthesecondlayerratherthanoverthefirstlayer.Inthenineteenth century,Gaussgaveasimpleargumentthatdemonstratedthepackingfractionin Eqs.(1.9)and(1.13)isanupperboundwhenidenticalspheresarearrangedin anykindoflattice.Curiously,theproofthatthisholdstrueforirregularaswellas
(a)
Sublattice A
Sublattice B
regularpackingarrangementshadtoawaittheendofthetwentiethcenturyand couldnothavebeencompletedwithoutreamsofpainstaking,computer-assisted analysis.Thisisthefamous Keplerconjecture fromaninfluentiallistofunsolved mathematicalproblemspublishedbyDavidHilbertin1900.
Doactualcrystalsfoundinnaturetakeadvantageofthesemathematical relations?Indeed,manyelementalmaterials,e.g.,thenoblemetalsgold,silver,and copper,crystallizeinthefcclattice.Hexagonallatticeswith c closetothevaluein Eq.(1.12)arealsoquitepopularinthenaturalworld(found,e.g.,inberyllium, magnesium,andzinc).Eventhebcclatticeisnotfarbehind,claimingthealkali metalsandsometransitionmetalssuchasironandtungsten.
Thepackingfractioncantakeusonlysofar.ThelatticestructureofgroupIV, III–V,andII–VIsemiconductorsisprimarilyduetotheelectronconfiguration intheoutershell.Inthesimplestcase,theoutershellsingroupIVmaterials suchasC,Si,Ge,and α -Sn(thelow-temperatureform)havetwo s andtwo p electrons.Astrongcovalentbondformswithotheratomsinthelatticeonlywhen theseelectronsaresharedwithuptofourothergroupIVatoms.Thefavored coordinationnumberoffourisevenlowerthaninthesimplecubiclattice.
Isthereaclose-packedlatticestructurewithacoordinationnumberoffour? Perhapswecanfindonewithabasis.Wesuperposetwospatiallydisplacedcopies ofoneofthelatticeswealreadyknow.Withtwointerpenetratingfcclattices,what displacementvectorleadstoacoordinationnumberoffour?Ifweshiftthesecond latticeby a/2alongallaxes,weformtherock-saltstructurefound,e.g.,intablesalt (NaCl).ButFig.1.6aillustratesthateachatominthelatticestillhassixnearest neighbors.
Thedesiredconfigurationhasfouratomsequidistantfromeachother,i.e., formingtheverticesofaregulartetrahedron(atriangularpyramid).Canwe embedthistetrahedronintothecubethatunderliesthefcclattice?Thisisawellknowngeometricalprobleminwhichtheverticesofthetetrahedroncorrespond tothe a/4 (1,1,1), a/4 (1, 1, 1), a/4 ( 1, 1,1),and a/4 ( 1,1, 1) verticesof theorigin-centeredcubeofsidelength a/2,asshowninFig.1.6c.Theatomsatthe verticesareconnectedbyvectors ±a/2 (1,1,0), ±a/2 (1,0,1),and ±a/2 (0,1,1), andthedistancebetweenthemis √2a.Infact,thesevectorsarethesameasthose linkingthenearestneighborsinthefcclatticeofEq.(1.8).Alloftheatomsat theverticesoftheregulartetrahedronareseparatedfromtheoriginbyadistance √3a/4.Ifthefirstlatticeincludesanatomattheorigin,andthesecondlattice isdisplacedbyadistance a/4 (1,1,1) fromthefirstsothatitincludesatomsat a/4 (1,1,1), a/4 (1, 1, 1), a/4 ( 1, 1,1),and a/4 ( 1,1, 1),wehaveacrystal structurewithfournearestneighborsthatcanaccommodatethe sp3 covalent bondingfoundinmostbulksemiconductors.ThisisshowninFig.1.6b. Whentheatomsofthetwointerpenetratingsublatticesarethesame,wehave the diamond crystalstructure,whichisfoundinnatureinthediamondformof crystallineC,Si,Ge,and α -Sn.Whentheatomsinthetwosublatticesaredifferent, asinIII–VsemiconductorsorsomegroupIVmaterialssuchasSiC,thecovalent
Figure1.6 (a)Rock-saltcrystalstructure,whichsuperposestwofcclatticeswiththesecond displacedbya/2 alongallaxes.(b)Diamondcrystallatticeformedbytwointerpenetratingfcc lattices.Whendifferentatomsoccupythetwosublattices,thestructureiscalledzinc-blende. (c)Aregulartetrahedronembeddedintoacubetoillustratehowacubiclatticecanaccommodate thevalenceofIII–Vsemiconductors.
bondispartiallyionicbecausesomeelectronsareclosertooneionthantheother. Thecrystalstructureisthencalled zinc-blende. Wecanalsoimaginetwointerpenetratinghexagonalsublattices.Eventhehcp latticeitselfcanbethoughtofashavingabasisthatconsistsofthefirstand secondatomiclayers,butwewilltakeittobeasingleunit.Iftwosuchlattices aresuperposed,theresulting wurtzite crystalisthedefaultforwide-gapIII-N semiconductorsandmanyII–VIsemiconductors,withtherelationbetween c and a inEq.(1.12)approximatelysatisfied.Table1.2summarizesthemostimportant typesof3Dlatticeandcrystalstructures,alongwiththeunitlatticeandbasis vectors.
Inthediamondandzinc-blendecrystals,thesecond-nearestneighborsare alwaysthesameastheatomattheoriginandidenticaltothefirst-nearestneighbors inthefcclattice.WewillseelaterthatthemostimportantfeaturesoftheIII–V
Table1.2 Themostimportant3Dlatticeandcrystalstructures,withcorrespondinglatticevectorsanddisplacementvector betweenthetwoatomsinthebasis,whereapplicable.
LatticeTypeLatticeVectorsBasisDisplacement
Simplecubic
Body-centeredcubic
Face-centeredcubic
Hexagonal
Hexagonalclose-packed
Diamond/zincblende
)
Rocksalt
Wurtzite
bandstructurecanbedescribedbytheunderlyingfcclattice,withthefinedetails emergingfromthefullzinc-blendesymmetry.
1.3OriginoftheBands Withthispictureinmindofhowtheatomsformalattice,wearereadytotackle thenatureofelectronicstatesinasemiconductorcrystal.Thesimplestcaseisan infinite1Dchainofatomswithperiodicspacing a,asinFig.1.7.Asanillustration ratherthanapracticalexample,imaginethatthechainconsistsofsomethinglike alkaliornoblemetalatomswithasingle s electronintheoutershell.
Theelectronicstateforthe s electroninthecrystalisdescribedbyitswavefunction.Thesquareofthewavefunctionistheprobabilityoffindingtheelectron ataparticularpointalongthechain.Sincethechainisinfinite,andoneatom looksexactlylikethenext,theprobabilitymustbethesameatallatomsand, moregenerally,atallpointswiththesamedistancefromanygivenatom.Inother words,theprobabilityisperiodicalongthechain,withperiod a.Thisdoesnot necessarilymeanthatthewavefunctionitselfisperiodicbecauseitcanhavean arbitraryposition-dependentphasefactor exp[i θ(x)].
Howdowefindthespatialvariationofthephase θ(x)?Imaginestartingat someatomandthenmovingafewatomstotheright.Becausethereisnothing todistinguishanyparticularatom,thewavefunctionatourdestinationcannot dependonthedeparturepoint,butsolelyonthedistancetraveled.Thishappens onlyifthephase θ(x) islinearin x,i.e., exp[i θ(x)] = exp(ikx).Ofcourse,a constantphase“background”hasnophysicalmeaning,sotheoriginisarbitrary. Weconcludethatspatialinvariancealongthechaintranslatesintoalinearphase variationwithdistance.Thecompletewavefunctionbecomes
where uk (x) isperiodicin x withperiod a.Thus uk (x) = uk (x + a) andingeneral isafunctionof k.Theperiodicfunction uk (x) maytellus,forexample,thatthe
V(x)
Figure1.7 Schematicillustratingasimplesinusoidalvariationofthepotentialenergyalonga chainofatomsspacedwithperioda.
electronsaremorelikelytostaybetweentheatomsthanattheircenters.Thisform ofperiodicpotentialisknownasthe Blochfunction.Forfreecarriersmovinginthe absenceofanypotential, uk (x) = 1,andthewavefunctioninEq.(1.14)isapure planewavewithuniformprobabilitydensityoverallspace.
FromEq.(1.14),thewavefunctionsatneighboringlatticesitesareconnected viawhatwecancallarecursionrelation:
Thesymbol k inEqs.(1.14)and(1.15)istheproportionalityfactordescribingthe particle’stranslation,knownasthe wavevector,orin1D,asthe wavenumber.Justas infreespace,itdeterminestheperiodoverwhichthewavefunctionoscillates,i.e., thewavelength 2π k TheBlochfunctionshowsthatthewavefunctionalsooscillates attheatomicscale,butthevariationdueto k maybemuchslower,i.e., 2π k a. If k variesbymorethan2π/a,thewavefunctionatagivenatomicposition na (n = 0, ±1, ±2, )repeatsitself.Thismeanstherangeof π/a to π/a isa completerepresentationofthe k dependence.Tokeepthingssimple,wehave chosenasymmetricrangeof k,butcouldhavecentereditatanyvalue k without losing(orgaining)anyinformation.
Toseethismachineryinaction,wecalculatethestatesinthesinusoidalpotential illustratedinFig.1.7:
whereforbrevitywehaveintroduced G ≡ 2π/a.Usingperiodicboundaryconditions,thewavefunctioncanbeexpandedastheFouriersum:
Inalargecrystal, q isessentiallycontinuous,andEq.(1.17)canbeconvertedto anintegralover q WewouldliketotransformEq.(1.17)intoanexpressionthatresemblesEq. (1.14).If k isconstrainedtotherange π/a to π/a,wecaningeneralwrite q = k + 2π l a = k + lG ,where l isaninteger.WecansubstituteourpotentialinEq. (1.16)andthetrialwavefunctionofEq.(1.17)intotheSchrödingerequation andletthechipsfallwheretheymay.Thekinetic-energyterminthatequationis p2 /2m,with p ≡−i ∂/∂ x.Forafreeparticle,theplane-wavewavefunctionmeans thatthemomentumisproportionaltothewavevector p = k.Thatis,thefaster theparticlemoves,themorerapidlyitsphaseoscillates.Infact,inthepilot-wave interpretationofquantummechanicsproposedbyLouisdeBroglieandexpanded byDavidBohm,particlesmovedeterministicallywithavelocityproportionalto thederivativeofthephase.Wecanalsolooselyassociate k with i ∂/∂ x,bysaying
thatitis dual tothespatialcoordinate x (orto ix).Weareinterestedinthe dependenceoftheenergies E andthecorrespondingwavefunctionson k, G ,and V0 thatfollowfrom
Wenowmultiplyby exp( iqx) andaverageovertheentirecrystal.Theaverageis definedastheintegraloverthecrystaldividedbyitslengthtakenintheinfinite limit,i.e., limL →∞ 1 L L 0 ... dx.Whenthecrystalisverylarge,thetermswithnonzerocomplexexponentialsoscillatesomanytimesthattheiraverageisnegligible. Therefore,weretainonlythose q componentsforwhichtheexponentsvanish. Thesurvivingcomponentsofthepotentialtermsatisfy q ± G q = 0or q = q ∓ G ,butintheothertermsonlythecoefficientswith q = q arenon-zero.Equation (1.18)becomes
Thissystemofequationsspansallvaluesof q,butonlythoseseparatedby ±G arecoupledbythepotentialterms.Thismeanswecanreplace q with k + lG (l = 0, ±1, ±2, ... )andrewritethewavefunctioninEq.(1.17)inareducedform:
Wehaveinsertedthesubscripttomakeitclearthatthewavefunctionhasavalueof k intherange π/a ≤ k ≤ π/a.Equation(1.20)hasthesameformasEq.(1.14), withtheperiodicpartgivenby
Nowthatweknowwhat q standsforinthiscase,Eq.(1.19)becomes 2 (k + lG )2 2m ak,l + V0 ak,l +1 + ak,l 1 = Eak,l (1.22)
Inthisform,werecognizethatthepotentialindeedcouplestheequationforany given l (bothpositiveandnegative)totwootherequations.Howcanwegoabout solvingtheseequations?Onewayistotruncatethe l termstomakethesystem
finite.Isthisreallyjustified?WeseefromEq.(1.22)thattheenergiesofthe k = 0 statesincreaserapidlywith l viathe 2 (lG )2 2m term.Soifweareinterestedonlyin thelowestenergystates,wemaydiscardthetermswithlarge l andincuronlya smallerror.Pushingtheconcepttoitslogicallimit,wemaybrashlyeliminateall thetermsexcept l = 0and l =−1(or,equivalently, l = 0and l = 1).Wedonot recommendthisprocedureforanypracticalsolids,buttheresultbelowretainsthe importantfeaturesofrealbands.Theadmittedlycrudeapproximationrewards uswith
Thisissomethingwecansolvewithoutmuchado!Amatrixequationwiththe generalform
hastheenergyeigenvalues
SubstitutingtheactualvaluesfromEq.(1.23)yields
Weseefromtheplotof ε± (k) inFig.1.8thattheenergiesarecontinuousfunctions of k.Thetwosignsleadtotwodistinct bands withdifferentenergiesatthesame k.Inthelower(upper)band,theenergymonotonicallyincreases(decreases)with k.Wenoticethatelectronicstateswithdifferent k valuesgenerallyhavedifferent energies.
Herethetwobandsareseparatedbyan energygap ofwidth2V0 ,withinwhichno electronicstatesexist.Themonotonicvariationoftheenergieswith k meansthey cannot“overshoot”intothegap.
Moregenerally,theFourierexpansionofthecrystalpotentialcontainsterms otherthan VG and V G fromEq.(1.16).Providedthat VG = V G = V0 ,the
Figure1.8 WavevectordependenceoftheenergyeigenvaluesofEq.(1.23).Atk = G 2 ,the eigenvaluesareseparatedbyagapof 2V0 .
energiesat k = G /2arestillclosetothevaluesinEq.(1.27);i.e.,thefundamental bandgapisnotaffected.Jumpingaheadalittle,theotherFouriercomponents VlG inthecrystalpotentialinduceadditionalgapsathigherenergies.
Steppingbacktotakestock,ourgambitwiththeminimalmodelofEq.(1.23) haspaidoffbeyondallexpectations.Wefoundthattheelectronsinsolidsresidein continuousbandsofstatesseparatedbythe“noman’sland”oftheenergygaps. Inourthree-dimensionalworld,thedispersionsaremoredifficulttocalculateand describe,buttherearestillbandsandgaps.Indeed,wehavestolenaglimpseofthe truenatureofelectronicstatesinsolidcrystals.Wearefortunatethatthisinsight cameatverylowcomputationalcost.
Nowwechangeperspectiveandregardthesameatomicchainfromanentirely differentangle.Theideaistosimplifytheproblembychoosingtherightbasis states.InthecaseofEq.(1.17),thosearesimplyplanewaves.Mightwedobetter ifwestartwithelectronwavefunctions φl (x na) “similar”tothoseoftheisolated atomsat x = na?Wedonotspecializeto s electronsjustyet,becausetheextra workwillpayoffinChapter5.Thesubscript l refersnowtotheatom’sdifferent electronicstates(s, p,etc.)Thecrystalpotentialisasuperpositionoftheatomic potentialsateachsite:
Wavefunctionsfortheelectronsintheatomicchainareformedbyaddingthe weightedcontributions φl (x na) foralltheatomicstates l summedoverallthe atoms.
WenextchoosecoefficientsthatsatisfyEq.(1.14).WeknowfromEq.(1.15) thatshiftingthewavefunctionby n atoms(i.e.,bythedistance na)isequivalent tomultiplyingbythephasefactor exp (ikna).Bypullingthatfactoroutofthe overallcoefficient,wecanincorporateeverythingweknowaboutthecandidate wavefunctionintoasingleformula: